中国PMI与GDP季节性协整分析
2016-03-26林俊凯暨南大学经济学院广州510632
■ 林俊凯(暨南大学经济学院 广州 510632)
中国PMI与GDP季节性协整分析
■ 林俊凯(暨南大学经济学院 广州 510632)
内容摘要:采购经理人指数PM I是评价宏观经济发展状况的一项先行指标,具有较大的市场影响力,是反映宏观经济态势的“晴雨表”。本文根据我国采购经理人指数(PM I)和国内生产总值(GDP)数据的季节性特征,运用HEGY季节性检验方法对二者进行季节性单整检验,并在此基础上进行季节性协整检验。本文的分析结果表明:我国PM I和GDP季节增长率在零频率和1/4频率上不存在季节单位根,在1/2频率上存在季节单位根,以二季为一个周期。我国PM I和GDP季节增长率在1/2频率上协整,说明二者存在长期均衡关系,用PM I来预测宏观经济走势是合理的。
关键词:采购经理人指数(PM I) 国内生产总值(GDP) HEGY季节性检验季节性单整 季节性协整

引言
采购经理人指数PM I是评价宏观经济发展状况的一项先行指标,具有较大的市场影响力,是反映宏观经济态势的“晴雨表”。当前全世界有20多个国家建立了PMI体系,PMI及其延伸的商业报告成为衡量宏观经济运行与变化的重要指标。PM I是以月度为周期的综合性经济监测指标,我国从2005年开始公布制造业PM I数据,2007年1月开始进行非制造业PMI调查,并于每月初公布。
PM I是一个综合的指数体系,涵盖体现宏观经济活动的多项指标,通常被认为与反映经济发展状况的国内生产总值GDP有密切关系。PM I以数值50作为经济发展枯荣的分界线,当PM I值大于50时,表明宏观经济运行状况良好,当PM I值小于50时,则意味着宏观经济在衰退。如果我国PMI与宏观经济运行具有较强的相关性,则PM I的研究与公布将有利于经济管理部门更好地进行宏观调控和政策引导,为金融机构、投资活动和生产企业提供决策依据,因此,基于这个前提,本文要研究的重点为中国PM I与GDP之间的关系。
PM I与GDP关系的相关文献综述
(一)相关文献综述
于颖、蔡进(2008)研究指出PM I对投资变化、工业总产值、固定投资等宏观经济指标具有先导性。于颖(2009)在另一研究中从方法论和实际验证的角度对我国PMI数据预测经济走势的功能进行研究,发现我国PM I对工业增加值、固定资产投资、工业品出厂价格(PPI)、海关进出口数据、股指等宏观经济指标具有预测作用。
张利斌等(2012)对我国PM I与GDP进行格兰杰因果关系检验,并且进一步建立了GDP与滞后4期的PM I指数回归模型,实证得出我国制造业PM I与GDP增速之间存在很强的相关性的结论。张利斌等(2012)进一步运用格兰杰因果检验和脉冲响应分析这两种实证方法对我国自发布以来的制造业PM I数据和同期GDP累积增速进行研究,结论为我国PM I与GDP累积增速之间存在着长期均衡关系,我国PM I大致领先于GDP变化趋势的时间为3-12个月。格兰杰因果检验表明我国PM I是GDP的格兰杰原因,而GDP不是PM I的格兰杰原因。
梁强等(2013)首先对我国PM I与GDP之间的关系进行理论分析,然后通过实证研究方法证实了我国PM I与GDP之间具有显著的正相关关系。
刘雪燕(2013)指出我国官方当前公布的PM I并未采用时间序列季节调整方法,而是在PMI调查之前确定调整因子,据此进行季节调整。我国官方PM I还具有明显的季节性,刘雪燕提出了更符合中国PM I的X-13季节调整方法,对我国官方PMI的季节调整提出改进建议。

表1 制造业PMI包含的各指标反映的经济现象
在早期,很多西方学者已经开始利用PM I数据对GDP和经济周期进行预测,如Dasgup ta and Lahiri (1993)发现PM I可以预测GDP的变化, Lind sey and Pavu r (2005)和Bane rjee and Ma rc e llino (2006)也都得出了类似的结论。在后来的研究中,一些西方学者运用不同的经济模型,以PM I作为自变量来预测更短期的GDP变化,研究表明通过PM I可以估计短期GDP走势。例如Cam acho and Perez-Quiros (2010)和 Kuzin, Marcellino and Schumacher (2011)。
(二)现有研究存在的问题
现有的研究可能存在如下问题:
一是在大多数使用季节数据的研究当中,学者对变量处理时使用一阶差分,这样隐含的假设是经济变量不具有季节模式,它们只有一个值为1的季节单位根,而不存在其他季节单位根。这样的处理是不恰当的,绝大部分季度数据都表现出很强的季节性,变量会有不同的季节单位根。
二是另一部分学者对于季节经济变量采用季节调整方法,如X-11与X-12方法,或基于此基础提出的X-13方法,以消除变量的季节成分,但是如果季节性波动恰是整个系统变化规律的重要来源,这样的处理方式会在一定程度上造成有效信息的损失。
三是在实际中,不同的时间序列数据在同一季节频率上的平稳性不尽相同,如果对变量直接建立回归模型,可能会产生季节虚假回归问题。中国PM I和GDP的数据具有较明显的季节性,本文运用HEGY季节性协整检验对二者进行分析,以规避上述问题。
GDP与PM I的相关性分析
理论上,PM I与众多宏观经济指标都有很强的相关性,其中最能代表总体宏观经济走势的是国内生产总值GDP。国内生产总值的定义为:在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,被认为是衡量一国经济状况的最佳指标。PM I分为制造业和服务业PM I,制造业PMI发源于美国20世纪30年代,包含新订单、产量、雇员、供应商配送、库存、价格、积压订单、新出口订单、进口等商业活动指标,每一项指标都与GDP密切相关。制造业PMI是一项综合指数,由生产、新订单、雇员、供应商配送与库存五类指标加权计算得到。服务业PMI体系包含商业活动、投入品价格指数、费用水平、雇员、未来商业活动预期等指数,但其建立时间不长,本文重点研究制造业PMI与GDP的关系。
我国制造业PM I综合指数采用国际通行做法,由加权指数计算得到。计算公式为PM I=订单指数×30%+生产指数×25%+雇员指数×20%+配送指数×15%+存货指数×10%。各项经济指标与GDP的相关关系如表1所示。
从表1可以看出,构成制造业PMI的各项指标直接体现了最终产品的供需状况,进而会影响到生产决策,如采购策略、生产计划、销售计划等。各项指标反映构成国内生产总值的最终产品的投入、生产、分配和需求,因此制造业PM I与GDP在理论上具有正相关性。
相关模型介绍
(一)季节性单整
定义:对在一年中S个等间隔时点取值的非平稳随机过程Yt,如果(ΔS)dYt是一个平稳可逆的ARMA过程,便称Yt是d阶季节性单整过程,记作Yt~SI(d) 。
通常,把一阶年度差分算子ΔS称作季节性差分算子。该定义表明,如果年度差分算子使得Yt成为一个平稳可逆过程,那么Yt~SI(1) 。在多数实际应用中,一般不考虑阶数d大于1的季节性单整过程。如果序列Yt可以通过季节差分算子ΔS=1-BS变成一个平稳序列,则序列Yt是季节单整的,也称序列Yt存在季节单位根。实际上,季节差分算子ΔS=1-BS会过滤掉季节性时间序列的随机趋势,比如S=4时,有:
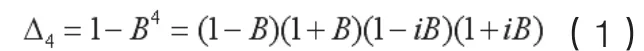
可见季节性时间序列可能含有4个模为1的根:1,-1,i,-i。当等式的根分别为1,1和±i时,称Yt在零频率、1/2频率和1/4频率上存在单位根,对应表示一季,二季和四季回到原值。
零频率单位根为1:(1-B)Yt=0,Yt=Yt-1,…;1/2频率单位根为-1:(1+B) Yt=0,Yt=-Yt-1,…;1/4频率单位根为±i:(1-iB)(1+iB)Yt=0,Yt=iYt-1,Yt-1=iYt-2,Yt-2=iYt-3,…;为了方便理解,我们假设Yt满足如下模型:
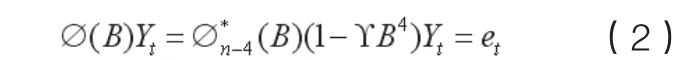
其中et为白噪声序列,中不含因子1-B和1-B4,如果γ=1,则Yt存在季节单位根。Hy llebe rg、Eng le、Granger和Yoo(1990)提出了一个简单的季节单位根检验方法,同时还可以检验非季节单位根,通常称为HEGY季节单位根检验:
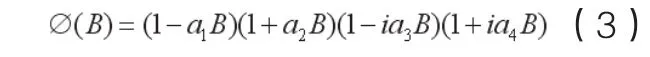
当a1=1,则序列Yt有一个单位根1,当a2=1,则序列Yt有季节单位根-1,以二季为一个周期,当a3=a4=1,则序列Yt有季节单位根i和-i,以四季为一个周期。HEGY(Hyllebe rg,Eng le,G range r,Yoo的简称,下文以此表示)进一步推导出了检验季节单位根是否存在的检验式:
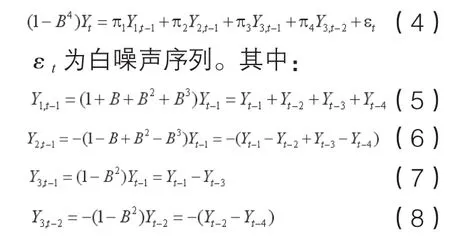
在对式(4)的回归分析中,如果π1=0的原假设不被拒绝,那么说明序列Yt在零频率上存在季节单位根1;如果π2=0的原假设不被拒绝,那么说明序列Yt在1/2 频率上存在季节单位根- 1;如果π3=π4=0的联合假设不被拒绝,那么说明序列Yt在1/4频率上存在季节单位根±i。HEGY建议对原假设π1=0和π2=0用t 检验,对原假设π3=π4=0则用F检验,HEGY详细分析了季节性单位根检验的方法。
(二)季节性协整:单一方程方法
单位根检验是协整检验的基础,当变量之间存在协整关系时,那么非均衡误差项应该是平稳的。由于变量在不同季节频率上的平稳性不尽相同,所以在季节性协整检验里要分频率进行,其中HEGY季节性协整检验方法应用最为广泛。HEGY和Enge l(通常简称EGHL)很早便对季节性协整检验展开研究。假设时间序列Xt、Yt~SI(1),令Xt0和Yt0表示经过HEGY变换后与零频率单位根相对应的变量,从而去除零频率上的单位根。
变换方式为:

当Xt0和Yt0在零频率上协整意味着存在唯一的线性关系使得:

其中ωt0~I(0),即回归残差是平稳的。类似地,在1/2频率上,假设和表示经过HEGY变换后与1/2频率单位根相对应的变量,从而去除1/2频率上的单位根。变换方式为:
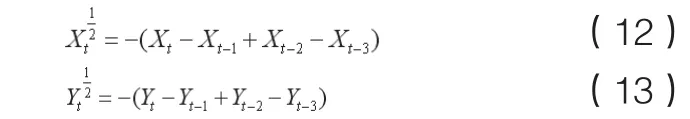



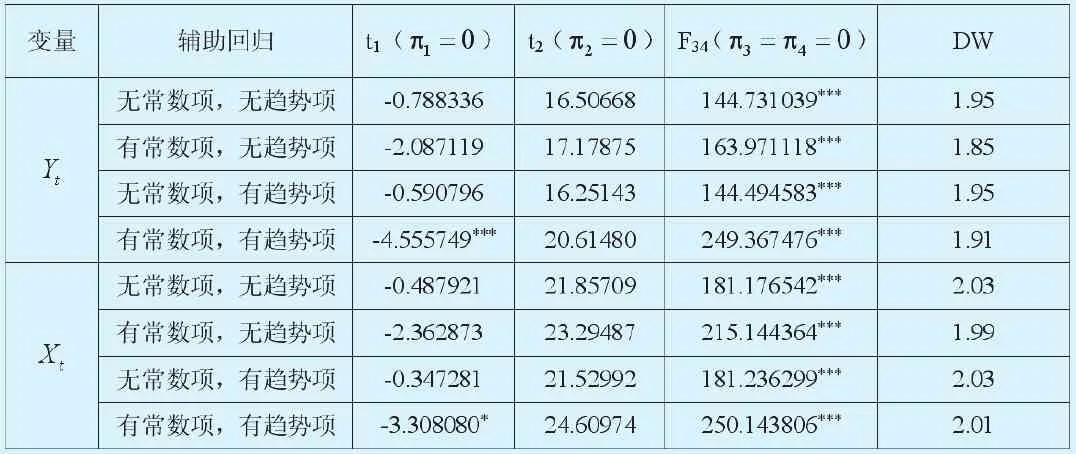
表2 HEGY季节性单位根检验

表3 1/2频率上Yt与Xt的季节性协整检验
数据说明与实证结果
(一)数据说明
本文使用我国制造业PM I与GDP增长率的季度数据,考虑到我国自2005年开始公布制造业PM I数据,因此本文样本区间为2005年第一季度至2015年第二季度。由于制造业PM I是月度数据,本文以同一季度内月度PM I算术平均值作为该季度的PM I数值。对于GDP,我国国家统计局公布的GDP绝对数是名义GDP,并未剔除价格因素,而GDP季度同比增长率是根据可比价格计算得出的,因此已经剔除了价格因素,是真实GDP的季度增长率。制造业PM I是百分数,GDP季度增长率也是百分数,二者有较好的可比性。在实证过程中,为方便数据处理,假设GDP季节增长率为Y,PM I 为X,本文对两个变量的数据不保留百分号。本文所有数据均来源于中国国家统计局官方网站。
(二)季节性单整结果
表2给出了HEGY季节性单位根检验的结果,对于Yt,π1=0的原假设在辅助回归中同时含有常数项和趋势项时不能接受,在其余辅助回归条件下不能拒绝π1=0的原假设。对于π2=0的原假设,在四种类型的辅助回归下都无法拒绝,在这种检验结果下,认为Yt在1/2频率上存在季节单位根。对于π3=π4=0的联合假设,在四种辅助回归下都无法接受。对于不同类型的辅助回归通过DW值都可以排除自相关的干扰。对于Xt,辅助回归中π1=0的原假设,在有常数项、有趋势项的情形下,t值小于10%的置信值,无法接受π1=0的原假设。对于π2=0的原假设,在所有情形下t值都大于10%的置信值,接受原假设。Xt在1/2频率上存在季节单位根。对于π3=π4=0的联合假设,F检验结果表明不能接受原假设,即Xt在1/4频率上不存在季节单位根。在不同辅助回归下,Xt也不受自相关的干扰。因此,GDP季节增长率和PM I在零频率和1/4频率上都不存在季节单位根,在1/2频率上都有季节单位根。
(三)季节性协整结果
根据表2的HEGY季节单位根检验结果,可以进一步检验Yt与Xt之间是否存在协整关系。表3表明GDP季节增长率和PM I在1/2频率上都含有季节单位根,可以采用单一方程方法利用式(14)对经过季节调整后的和进行回归得到残差项。对的单位根检验结果如表3所示,可以看出,是平稳的,所以GDP季节增长率和PM I是季节性协整的,即二者之间存在长期均衡关系。而在零频率和1/4频率上,GDP季节增长率和PMI没有同时具有季节单位根,所以无法进一步进行季节性协整检验。
结论
我国PM I和GDP季节增长率在零频率和1/4频率上不存在季节性单位根。一些研究忽略两个变量的季节性,直接对它们进行一阶差分的处理是欠妥的。在1/2频率上,我国PM I和GDP季节增长率同时具有季节单位根。我国PM I和GDP季节增长率在1/2频率上协整,表明两者之间存在长期均衡关系。以PM I作为反映宏观经济的“晴雨表”是合理的,但是不能忽略变量的季节规律。如果忽视季节性,对二者关系的认识是不准确的。我国公布的GDP和PM I数据虽然有经过季节性调整,但是调整效果不理想,二者都还具有季节性,因此需要建立更有效的季节调整体系,以更好地利用PMI来预测宏观经济走势。
参考文献:
1.刘雪燕.PM I指数季节调整研究[J].中国物价,2013(5)
2.梁强,刘嘉琦,翁潘林.PM I指数与中国GP增长率:基于有效性和设计合理性视角的研究[J].专家论坛,2013(8)
3.张利斌,冯益,刘龙飞,张竹.制造业PM I 对GDP 走势的预测作用[J].中南民族大学学报(自然科学版),2012(9)
4.张利斌,冯益.中国PM I 与GDP关系的实证研究[J].统计与决策,2012(2)
5.于颖,蔡进.中国PM I(采购经理人指数)与其他数据相关性研究(二)[J].社科纵横,2008(12)
6.于颖.中国PM I数据的实际应用—PM I的领先性分析[J].社科纵横,2009(12)
7.Dasgupta S,Lahiri K. On the Use of Dispersion Measures from NAPM Surveys in Business Cycle Forecasting[J]. Journal of Forecasting ,1993,12(3&4)
8.Lindsey M D,Pavur R. As the PM I turns: A Tool for Supply Chain M anagers[J]. The Jou rnal o f Supp ly Chain M anagement,2005,41(3)
9.Banerjee A,M arcellino M. Are There Any Reliable Leading Indicators for the USIn ation and GDP Grow th?[J]. International Journal of Forecasting,2006,22
10.Cam acho M,Perez-Quiros G.Introducing the EURO-STING: Short Term Indicator of Euro Area Grow th[J]. Journal of Applied Econometrics,2010,25(4)
11.Kuzin V,M arcellino M,Schumacher C. M IDAS vs M ixed-Frequency VAR for Now-casting GDP in the Euro Area[J]. International Journal of Forecasting,2011,27
12.Hylleberg S,Engle R F,Granger C W J,Yoo B S. Seasonal Integration and Cointegration[J]. Journal of Econometrics,1990,44
林俊凯(1989-),男,汉族,福建漳州人,暨南大学经济学院金融学硕士研究生,研究方向:货币理论与货币政策。
作者简介:
中图分类号:◆F224.9
文献标识码:A
