基于Kd树改进的高效K—means聚类算法

高亮谢健曹天泽

摘要：针对经典的Kmeans算法在多维数据聚类效率上还有待提高的问题，本文提出一种称为CKmeans的改进聚类算法。该算法在kmeans算法的基础上，通过引入Kd树空间数据结构，初始聚类中心从多维数据某一维的区间等间隔集中选取，以及在数据对象分配过程中采用剪枝策略来提高算法的运行效率。实验结果表明，CKmeans聚类算法较经典的kmeans聚类算法运行效率更高。

关键词：kmeans算法；簇心；kd树；剪枝策略；CKmeans算法

中图分类号：TN914文献标识码：A

1引言

数据挖掘是一种经典有效的数据分析方法，聚类分析是数据挖掘中的重要研究内容。数据对象通过聚类分析，可以形成簇或者类内部数据对象相似度高且不同簇之间的数据对象相似度低的簇组。目前主要的聚类方法有：划分方法、层次方法、基于密度的方法、基于网格的方法和基于模型的方法[1]。kmeans算法是一种传统的聚类算法，其算法易于实现、时间复杂度小和可以处理大型数据集等优势明显。

Kmeans算法作为一种常用的聚类算法，在处理多维和海量数据时，由于需要提前给定簇的个数，聚类结果随初始质心变化的波动大，重新计算质心时受到孤立点影响，而且仅适用于类簇之间区别较大的情况，同时聚类过程时间消耗过长，因此提高该算法的执行效率。

在文献[2]中，李涛等提出了一种引入竞争策略的聚类算法。受文献[2]、[3]的影响，本文提出一种kmeans算法的改进算法称为Ckmeans算法。该算法从多维数据中随机选取某一维数值并均分为k个数值域。初始聚类中心从k个数值域中选取，以减少迭代次数来提高算法效率。引入了K-d树，对样本点的数据结构进行标准化，从而便于节点的遍历和查询。同时，该算法采用了剪枝的策略，减少参与计算节点和候选聚类簇心之间欧式距离的计算量，从而能够明显地降低算法时间复杂度。在剪枝时，计算最小距离时利用k-d树最近邻查询算法，计算最大距离时利用数据节点代表的空间范围最大值，从而大大提高了剪枝策略的有效性。通过对传统的kmeans聚类算法进行此方法的改进，进而提高了算法的运行效率。

2Kmeans 算法

2.1Kmeans 算法简介

Kmeans算法是一种基于划分的传统聚类方法，该算法的基本思想是：在n个数据对象中，首先随机初始化k个簇心，每个点分派给最近的簇心，分派到同一个簇心的所有数据对象的集合构成一个簇，接着根据分派到簇的点，更新每个簇的簇心，重复分派和更新簇心过程，直到簇的簇心不发生变化，最终得到目标函数最小的k个类。

计算技术与自动化2015年12月

第34卷第4期高亮等：基于Kd树改进的高效Kmeans聚类算法

2.2Kmeans 算法的优势

Kmeans算法是一种高效的聚类算法，在科学研究和工程应用中得到了应用和推广，它的算法流程比较简单，并且收敛速度很快，对于大数据集也有较好的分类效果，其时间复杂度为O（tkdn）， t是迭代次数，k是簇类的个数，d是数据集的维数，n是样本点数。在对大型数据集聚类时，Kmeans算法比层次聚类算法快得多[4]。

2.3Kmeans 算法的不足

1）必须提前给定要形成的聚类个数k。

Kmeans算法必须提前给定要形成的聚类个数k，聚类的结果对此有很大的依赖性，然而通常最恰当划分数据集的聚类的个数并不是事先可知的，一般需要通过多次反复试验才能得到该聚类个数，因此在算法的开始就指定聚类个数会影响聚类过程和结果是很明显的。

2）聚类结果随初始聚类中心变化的波动大。

Kmeans算法随机指定初始聚类中心，这给聚类结果带来很大影响，聚类结果变得不稳定，有可能导致局部最优。

3）重新计算质心时受到孤立点影响。

在聚类的迭代过程中，要重新计算以形成新的质心，但是与类簇距离明显的孤立点导致计算的质心也偏离真正的数据密集区，质心的代表性下降，新的聚类过程受到孤立点的影响大。

4）仅适用于类簇之间区别较大的情况。

由于Kmeans算法根据欧式距离度量各个点之间的距离，并且聚类准则函数使用偏差和准则函数，聚类过程参考该准则函数。只有当类簇之间区别明显是，聚类才会有效，否则可能导致聚类的过程反复不定，不断将形成的类簇分割的情况。

5）聚类过程时间消耗。

Kmeans算法的聚类是一个不断的迭代的过程。一旦形成类簇，就重新计算质心，然后重新计算距离并指派，当解决大数据量的问题时，算法的聚类过程会消耗大量的时间。

本文针对Kmeans算法对海量数据和多维数据运算速度慢，时间消耗大的缺陷，提出改进算法CKmeans，以期提高算法的运算效率。

3KD树

Kd树（多维二叉搜索树）是由Bentley于1975年提出[5]，k是空间数据对象的维度数，在多维的空间数据结构中，Kd树常用来数据索引和数据查询。kd树通过把一个空间划分成多个不相交的子空间来进行高效的组织k维空间中点的集合。kd树中内部节点对象包含有某一维的区分值，其中小于或等于区分值的点划分到左子树，大于区分值的点划分到右子树。Kd树本质上是一种二元搜索树，它用超平面把一个空间划分成若干子空间来对数据搜索，可以快速而准确地找到某一点的最近邻。

3.1Kd树构造算法

Kd树的构造是多次使用垂直于坐标轴的超平面分割k维空间实现的，所有的对象都组织到树中，其中根节点代表所有的对象。

在Kd树的构造中，一方面考虑在数据对象维度进行分割时，选择基于顺序循环分割或者基于维的长度优先分割；另一方面考虑分割点的判断，选择基于中点的方法或者基于中值点的方法。在文献[6]中的研究表明，这两个因素的选择分别为从最长的维度开始分割和选择中点的方法较好，本文采用上述方法。Kd树构造是多次递归地调用Kd树构造函数实现的，Kd树构造算法的时间复杂是O（nlogn）。

Kd树的构造算法[7]如下：

输入：维度为d的数据对象集合X和Kd树的深度Depth；

输出：包含所有数据对象的Kd树根节点KD。

1）若数据对象集合X为空，返回空Kd树；

2）调取节点判断的函数，

（1）计算数据对象每一维数值的方差值，分割维Split的顺序按方差大小来判断，

（2）取每一维的中点值作为分割点MidPoint；

3）在Split维时分割点MidPoint划分数据集合，得到子集合X1和X2，X1：在Split维的数据对象都小于或等于MidPoint，X2：在Split维的数据对象都大于MidPoint；

4）Lchild为KD的左子节点，Rchild为KD的右子节点，Lchild=KdConstruct（X1，Depth+1），Rchild=KdConstruct（X2， Depth +1），递归地调用直到子节点为叶子节点；

5）把Lchild和Rchild 合并为Node，返回Node。

3.2Kd树上的最邻近查找算法

Kd树是一种很好寻找最近邻问题的数据结构，Kd树的查找有最近邻搜索和范围搜索两种基本方式。Kd树上的最邻近查找算法即在Kd树中检索与某一查询点欧式距离最近的数据点[8-9]。kd树最近邻查找算法描述如下：

输入：Kd树类型的KD和查找对象Object；

输出：最近邻数据点。

1）若数据KD为Null，返回；

2）从根节点递归地向下搜索，进行二叉搜索；

3）搜索到叶子节点，记为当前最近邻Nearest；

4）回溯搜索：

if 超球与父节点超平面相交，进入相反的空间搜索，更新Nearest，else继续向上回溯，父节点相反的空间不查找；

5）回溯到根节点，结束并返回最近邻。

4Ckmeans算法

本节内容为Ckmeans算法的详细设计描述。

4.1Ckmeans 算法设计

在改进Kmeans算法过程中，通过对Kmeans算法运行时间进行分析来提出改进，提高算法的运行效率。设初始簇心时间为Tinit，分派样本点时间Tassign，重新计算簇心时间为Tagain，Kmeans算法迭代次数为t，Kmeans算法的运行时间Tsum。则有以下算法的运行公式：

Tsum=Tinit+tx（Tassign+Tagain）…（1）

由公式（1）可知，若要提高算法的运行效率，可以通过减少算法的迭代次数和指派时间来实现。

对于d维数据集X，在d维选取其中的一维数值，对该维数值进行排序，则存在一个对应的区间[m，n]，给定一个整数常量k，把区间[m，n]分成k个子区间，子区间长度是相同的，则规定C={C1，C2，...，Ck-1}为区间等间隔集，当i=1时，C1=（m-n）/k；当i=2，3，…，k-1时，Ci=Ci-1+C1。pkmeans算法的k个初始簇心分别从C（k等分）的每一个子区间中选取。通过对kmeans算法选取初始簇心的随机性进行改进，达到减少迭代次数来提高Ckmeans算法运行效率的目的。

在Kmeans算法分配数据样本点的过程中，需要保证数据集X中的样本点被指派给最近的簇心，当所有样本点分配结束之后，重新计算簇心。Kmeans算法对于X中的样本点，需要计算其与所有簇心的距离，然后找到最近距离的簇心。

在Ckmeans算法中，通过引入Kd树，使得样本点数据结构标准化，便于遍历和查询。通过采用剪枝策略，减少了要参与计算的点和候选簇心的欧式距离计算量，可以显著的减少算法的时间复杂性。剪枝策略：首先搜索候选簇心集中的每个簇心到该节点对象所代表的空间区域的最近邻距离MinDis，最小距离采用Kd树最近邻查询算法获取，然后把该节点对象所代表的空间区域的最大距离记作MaxDis，最大距离采用节点所代表的空间范围的最大值，最后把最近邻距离大于最大距离的最小者的簇心剪去。

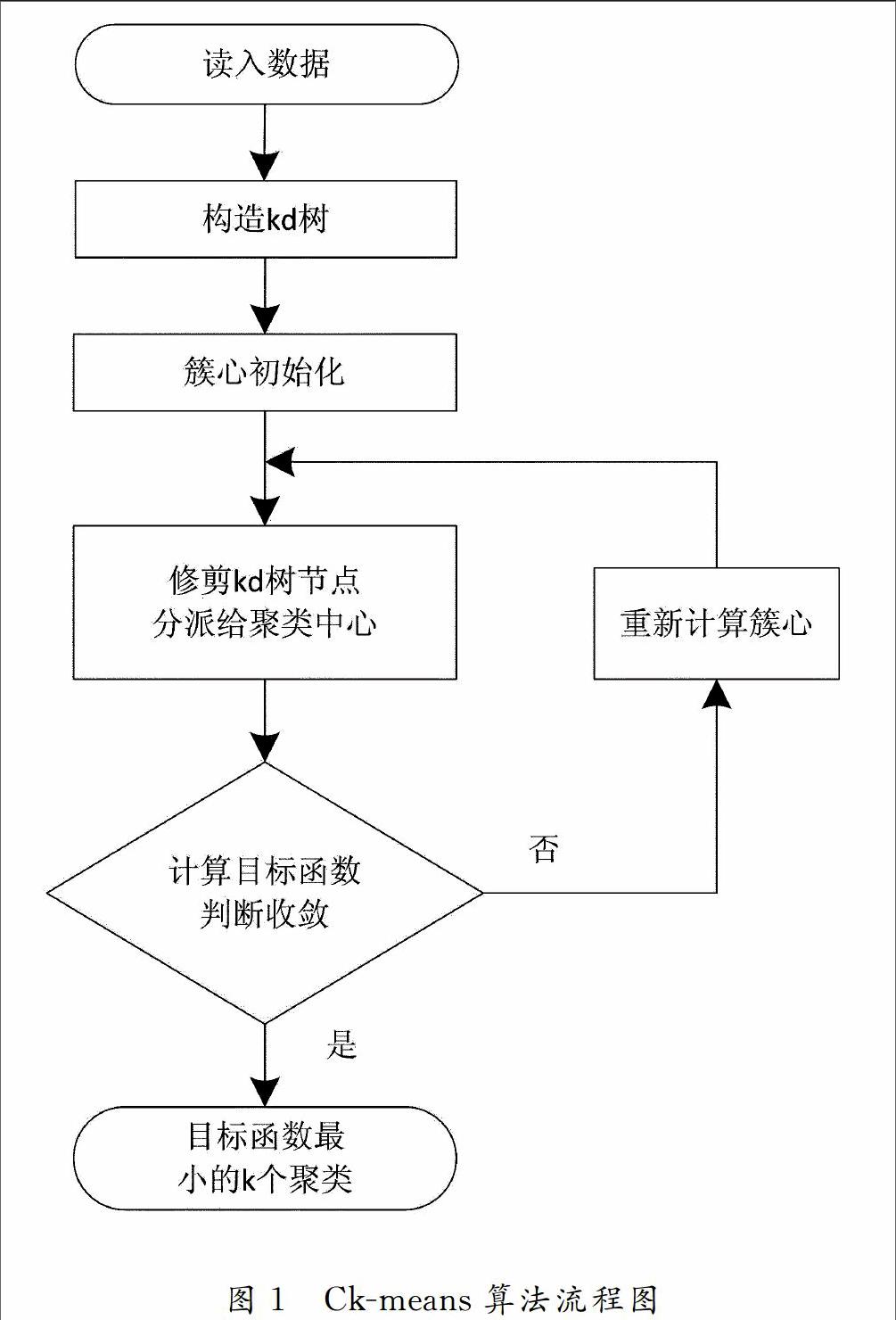
Ckmean算法的基本思想是：将数据集初始成Kd树，从d维数据集X中选取一维数值，排序后形成区间等间隔集，得到算法的初始簇心集。从初始化后的Kd树的根节点对象开始，根据最小距离最大距离原则剪枝，根节点对象于全部候选簇心集计算欧式距离，而子节点只从父节点的候选簇心集剪枝。分配数据对象后，再次计算簇心，直到目标函数值收敛。如图1所示，Ckmeans算法可以描述：

输入：聚类个数k以及包含d维的n个数据对象数据集X；

输出：满足目标函数值QUOTE最小的k个聚类。

1）将样本集合X构造Kd树；

2）簇心初始化，在数据集d维中取一维排序成区间等间隔集，取k个初始簇心；

3）修剪节点对象的候选簇心集；

4）计算节点对象到修剪后的候选簇心的距离并当距离最小时把对象Xi分配给簇Cj；

5）重新计算：重新计算与簇心；

6）重复步骤3）和4），直到值收敛。

4.2Ckmeans 算法中剪枝策略

剪枝原则如下：首先搜索候选簇心集中的每个质心到该节点对象所代表的空间区域的最近邻距离MinDis，然后把该节点对象所代表的空间区域的最大距离记作MaxDis（在构造kd树的过程中形成的数据结构），最后把最近邻距离大于最大距离的最小者的质心剪去。

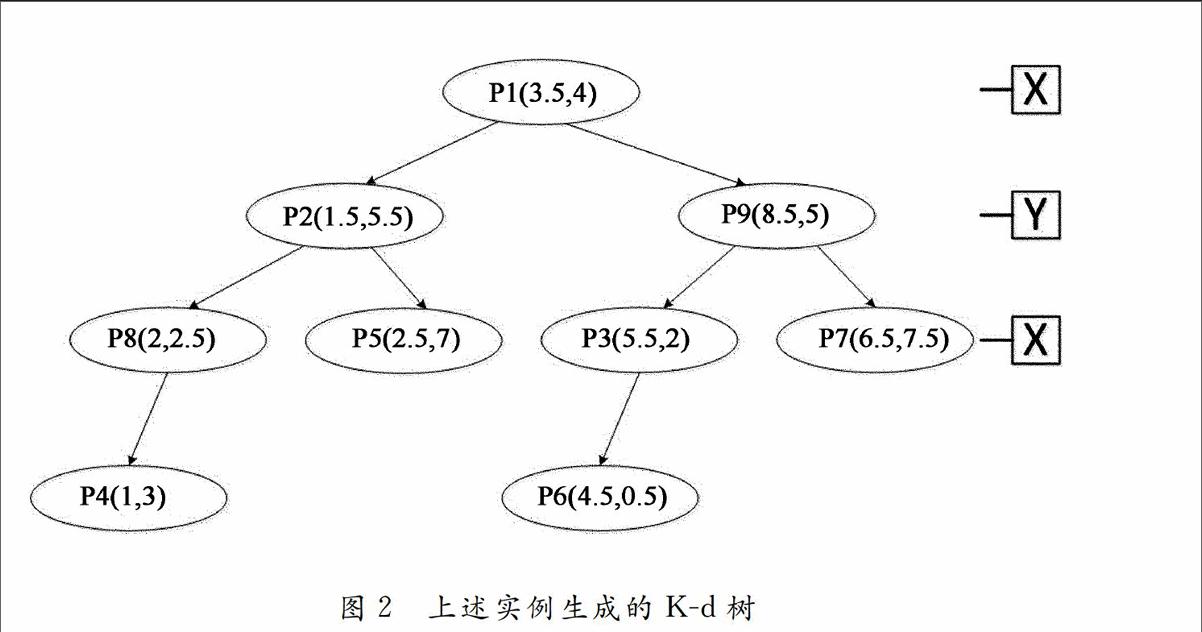
具体的剪枝策略如下：假设存在一个数据集合X，数据集X为{（3.5，4），（1.5，5.5），（5.5，2），（1，3），（2.5，7），（4.5，0.5），（6.5，7.5），（2，2.5），（8.5，5）}，对该数据集构建K-d树结构如图2所示：

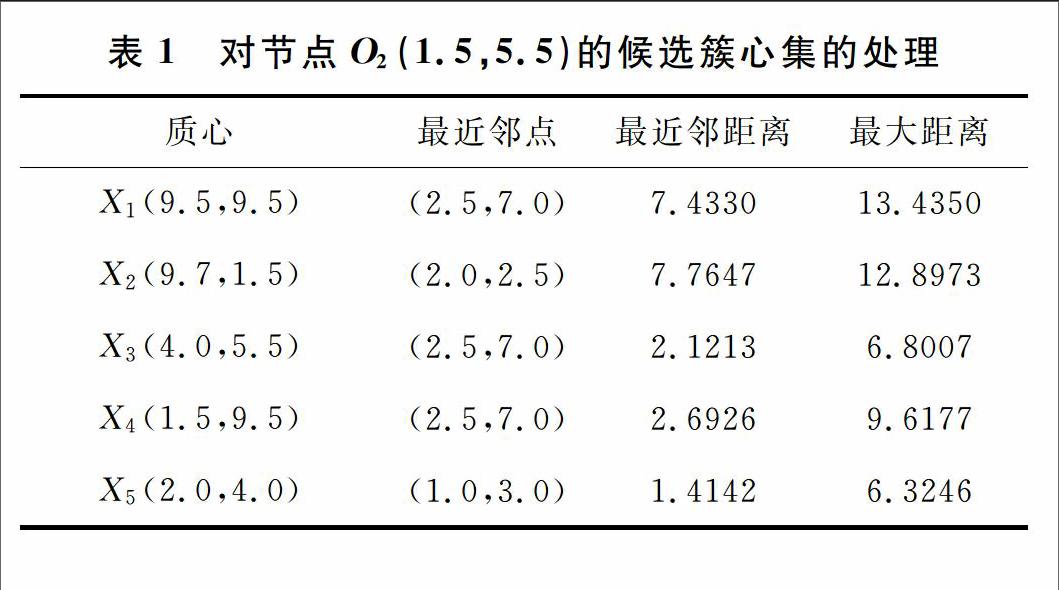
已经选择的候选簇心集为：{（9.5，9.5），（9.7，1.5），（4，5.5），（1.5，9.5），（2，4）}，根节点为O1（3.5，4.0），候选簇心集为{ X1，X2，X3，X4，X5}，该点被指派给质心：X3；根节点的左叶子节点O2（1.5，5.5），所代表的空间范围为（1，2.5）和（3.5，7）所包围的矩形，父节点的候选簇心的个数为：5，即{ X1，X2，X3，X4，X5}，针对5个候选簇心有如表1的计算结果。

如表所示，其中最大距离中的最小者为6.3246。将最近邻距离大于最大距离的最小者的质心剪去后，只剩下3个质心，即{X3，X4，X5}。则针对左叶子节点O2（1.5，5.5）的候选簇心集为：{X3，X4，X5}，该点被指派给质心：X5。对于各个候选簇心与该节点对象的最近距离与最远距离表示如图3所示。以此类推，对节点O2（1.5，5.5）的左叶子节点O8（2，2.5）也进行剪枝，其中参与剪枝的候选簇心集合只从其父节点的候选簇心集合中选取，结果是{X3，X4，X5}，在剪枝工作之后的候选簇心集合是{X3，X5}。对于其他的节点对象也采取相同的操作策略，对数据集合所构建的k-d树的左子树上的各个节点，在采取了剪枝操作之后，相应的候选簇心情况如图4所示。

从图4中我们可以看到，在经过了剪枝操作之后，每个节点都拥有相应的候选簇心集合，并且这个候选簇心集合中质心的个数明显少于初始的整体簇心集合，如此就能减少节点与质心之间欧式距离的计算量，从而有效地减少运算时间，提高了运算的效率。

5实验结果及分析

在试验中，算法的程序用Java语言实现，编译环境为Eclipse。实验的计算机环境为： Intel（R） Core（TM） i3-2120 CPU，3.30 GHz，2.85G内存，操作系统为windows XP Sp3。

本文用到的测试数据集来源于文献[10]中，并没有数据集进行任何特殊的优化。为了体现算法对不同数据规模体现的效率，选用2个测试数据集对Kmeans和Ckmeans进行实验，分别是data[1024，2]和data[1024，10]。data[1024，2]数据集表示由1024个数据点和2维属性构成，data[1024，10]类同。在这2个数据集上对k=20、30、40、50、60、70、80、90分别进行测试。针对每种情况进行20次试验。

实验结果如下图5和图6所示。由实验结果分析可知：与Kmeans算法相比，Ckmeans算法在精度上与其近似，但是Ckmeans算法在运行效率上明显优于Kmeans算法。

1）在运行效率上，Ckmeans算法优于Kmeans算法，随着数据集维度增加和聚类个数的增加，Ckmeans算法的优势更加明显。当数据集维度为10时，Ckmeans算法的运行时间相对于Kmeans算法的节省了2～3倍。

2）当数据集维度为2时，Ckmeans算法的运行效率优势比较微弱，但在此数据规模下当聚类个数不断增加，Pkmeans算法的运行效率优势显示出来。

6结论

通过对经典Kmeans的分析和研究，为了提高算法的运行效率，对Kmeans算法进行改进。改进的算法优化了传统随机选取簇心的初始化方法，提出了基于Kd树和剪枝策略的Ckmeans算法。经过实验结果比较，改进后的算法与原有算法具有相似的精度，但是改进后的算法的运行效率明显提高，尤其是对于高维数据效果更明显。把它应用在农业气象灾害区划系统之中，对于提高气候区划的精度，以及系统的反应速度都有着比较好的参考价值和意义，同时对满足其他科学的研究和工程应用需求也提供了非常良好的借鉴作用。然而，这仅仅是在数值计算领域得到了验证，如何将其应用于非数值数据的聚类分析与计算中，仍然是今后的研究方向。

参考文献

[1]WANG Qian，WANG Cheng.Review of Kmeans clustering algorithm[J].Electronic Design Engineering，2012.

[2]Tao Li，Shuren Bai，Jinyang Ning.An improved Kmeans Algorithm Based on Competitive Strategy[J].In： International Conference on Information and Multimedia Technology.Hong Kong：IEEE Computer Society，2010，2：76-80

[3]ZHAI Dong-hai，YU Jiang，GAO Fei.K-means text clustering algorithm based on initial cluster centers selection according to maximum distance[J].Application Research of Computers.2014.

[4]HUANG Z.A fast clustering algorithm to cluster very large categorical data sets in data mining. In： Tucson： the SIGMOD Workshop on Research Issues on Data Mining and knowledge Discovery.Tuncson， 1997， 146～151

[5]BENTLEY J.Multidimensional binary search trees used for associative searching[J].Journal of Communications of the ACM， Vol.18， No.9： 509- 517，1975.

[6]Jiang Xiaoping，Li chenghua.Parallel implementing kmeans clustering algorithm using MapReaduce programming mode[J].J.Huazhong Univ.of.Sci&Tech.（Matural Science Edition）.2011

[7]Chen Xiaokang，Liu Zhusong.K Nearest Neighbor Query Based on Improved KdTree Construction Algorithm[J].Journal of Guangdong University of Technology.2014

[8]MOORE A W. An introductory tutorial on kdtrees[D]. Extract from Andrew Moore's PhD Thesis： Efficient Memorybased Learning for Robot Control Technical Report No. 209.1991

[9]STEPHEN J.Redmond，Conor Heneghan.Method for Initializing the Kmeans Clustering Algorithm Using Kdtrees[J]. Pattern Recognition Letters， 2007，28（8）：965-973.

[10]HAN Lingbo.A new method of determining optimal number of clusters Kmeans[J].Modern Compute.2013，20：46-50.