高校排考系统资源冲突优化算法的研究

岳沙沙

摘要：随着高校学生人数的不断增加，教学资源匮乏问题日益明显，使得考务安排工作变得繁重且繁琐。为解决高校排考系统资源冲突优化问题，文章根据高校的考场安排问题进行了分析、抽象以及数学描述，通过构建简单无向图利用蚁群算法来解决排考时间安排的冲突问题；利用循环队列方法解决监考教师安排的冲突问题；提出了一种考场安排算法解决排考问题中的考场安排问题。文章针对各类排考资源（教室、监考教师、考试时间等）在最优考试时间段的选取组合优化问题，构建了具体算法描述过程，解决了考试时间安排、考场安排及监考教师安排三者的冲突问题，应用该方法使得排考系统资源冲突优化问题得以解决，自动排考系统运行效率得到了提高，各类排考资源之间的冲突现象明显减少，进而提高了高校教务管理人员的工作效率。

关键词：高校排考系统；简单无向图；循环队列；考场安排；蚁群算法；组合优化

考场安排是高校考务管理活动的主要组成部分，由于排考冲突条件多，数据量大，人工排考无疑是一种繁复、琐碎的工作。面对我国高校因扩招而带来的教育资源配置不足与培养方式多样化之间以及教学资源短缺与考试方式多元化之间日益严重的矛盾，需要在各高校开展教育国际化和协同创新体系，为适应新时代的要求，实现学生考试管理方式的智能化就显得十分必要。

1 排考问题分析

排考问题是要解决资源的有序组合，属于时间表问题。研究如何把高校的教师资源、教室资源、学生、班级、课程、考试时间资源等排考资源有机结合，从而使组合得到的资源是最优的，也即场次尽量地少而安排合理的考试考场时间安排表。这些排考资源之间是相关的，在排考过程中可谓牵一发而动全身，要实现排考过程的最优化，则需要在多约束条件下，通过多种优化规则，使现有的排考资源在编排过程中最大程度地达到最优化。

总体来说，排考主要解决的问题是同一名考生不能在同一个时间段内考多门课程（考试时间安排）；同一名教师不能在同一时间段内监考多门课程（监考安排）；一个考场不能在同一时间段内安排多门课程（考场安排）。也即解决考试时间安排、监考安排、考场安排这三者之间的冲突问题并且排考结果要求考生的各门考试课程之间要有一定的时间间隔以保证考生有足够的调解时间。抽象的排考问题已经被证明是一种NP难问题，至今没有一种能适用于所有情况、结果普遍令人满意的解。

2 排考问题数学描述

在考试安排的过程中，主要涉及时间、考场、教师、学生、课程、班级这6个实体集合。以下是对这6个实体集合的定义：

（l）时间集合：

T={t₁，t₂…t_n}，共有n个考试时间段。

（2）考场集合：

R={r₁，r₂…r_m}，共m个考场用于考试安排。

（3）教师集合：

P={p₁，p₂…p_i}，共有i个教师参加监考。

（4）学生集合：

S={s₁，s₂…s_j}，共有j个学生参加考试。

（5）课程集合：

C={c₁，c₂…c_k}，共有k个课程需要安排考试。

（6）班级集合：

Z={z₁，z₂…z_l}，共l个班级需要安排考试。

根据这6个实体集合构造简单无向图G=（V.E，c），其中V代表顶点集，每一门考试科目代表一个顶点，共有k门考试科目，则图G中共有k个顶点。

V={v₁，v₂…v_k}。

E代表各项点相互连接所组成的边集。如果有考生同时参加某2门考试科目的考试，则对应的顶点之间有边相连。

c为各边权值的集合，定义为共同参加该边连接的2个顶点对应的考试科目考试的考生人数。如果有n个学生同时参加和这2门课程的考试，则v_i和v_j之间就有1条边相连，即e_ij。边的权值为n。

G的邻接矩阵B=（b_ij）_kxk一个对称阵，其维数为考试科目数，矩阵B中元素取值如下定义：

通过邻接矩阵B的构建，可见考试课程间的关系仅有2种表示方式，即相容（不存在1个学生同时选修2门课程的情况）；相斥（存在至少有1个学生同时选修2门课程的情况）。因此，用O表示相容，则2门课程同时安排在同一考场的条件完全满足；而用1表示相斥，则2门课程同时安排在同一考场会引起课程冲突。 将上述邻接矩阵B进行简化，得到考试课程关系矩阵 矩阵M中元素取值如下：

依据课程关系矩阵M，可以得到如下2类数据：

（1）课程关联系数 ，其中k代表课程数。课程关联系数的值越大，代表课程之间的相容性越差，即与其他课程组合能力越弱。

（2）与第i门课程相容的课程候选集，由满足 条件的所有课程组成。

由关系矩阵M得出的2类数据可见，本文提出的排考算法为了使整个排考结果得以合理优化，首先必须保证“考试课程之间在资源分配上无冲突”，满足安排考试场次最少，尽可能使连考的学生数量少。

根据上述定义，将三元组t₁：<学生，课程，班级>看作事件，三元组t₂：<时间，考场，教师>看作资源，排考问题就转化为事件t₁分配合理的资源t₂，也就是解决时间、考场及教师之间的冲突问题。

3 相关算法的构建

3.1 考场时间安排算法

考场时间安排是排考过程一项重要的任务，科学、合理的考场安排方法不仅可以提高考试安排工作的效率，而且可以解决人工排考过程中出现的问题。因此，在安排考场时，首先需解决的问题是如何将选修同一门课程的学生安排在同一考场同一时段进行考试且同一时间段内1个学生只能参加1门课程考试。

时间安排从算法实现上来讲可分为2个过程：从排考问题中抽象出图论的模型，将时间安排算法转化为蚁群算法，得出多组可用解；再从可用解中选取相对较好的解作为最终结果。

在使用蚁群算法求解考试时间安排优化问题时，蚂蚁需要具备以下行为特征：

（l）蚂蚁通过利用第2小节构建的简单无向图G={V，E，C}来寻找最优解X^*。

（2）蚂蚁具有记忆能力。与现实中的蚂蚁不同，本文所采用的蚁群算法的人工蚂蚁具有记忆能力，每个蚂蚁对应一个禁忌表M'，禁忌表M'中主要是用于：①帮助蚂蚁记住该蚂蚁在此次循环中，图中哪些考试科目已经分配过时间，哪些考试科目还没有分配，从而避免再次选择已经选择过的考试科目。②蚂蚁从图G的某一个顶点选取下一个顶点的概率是与该2点之间的权值有关的启发信息η和边上存有的信息素量的函数。这个概率直接反映的是考试科目之间的期望关联程度。通过禁忌表蚂蚁记住当前选择的顶点，帮助确定2点之间的权值，计算启发信息η，从而决定蚂蚁选择下一个顶点的概率。这样蚂蚁们可以知道哪个考试科目安排在当前的时间点相对较合适。③蚂蚁完成一次循环以后，通过禁忌表构建出一个可行解，计算出目标函数值，并且可以同其他蚂蚁循环后的目标函数值进行比较，找出最小目标函数值所对应的可行解。此后，禁忌表被清空，蚂蚁可以进行下一次的循环。

（3）蚂蚁按照概率选择策略进行移动。概率选择策略增加了路径随机选择的可能性，避免算法过早收敛于局部的解。概率选择策略是一个关于局部可用的信息素和启发信息（即蚂蚁所在的图G中当前位置的邻域上与顶点连接有关的信息素和启发信息）的函数。

（4）一旦蚂蚁建立了一个可行解，它可以按照原路返回并在返回的过程中对连接顶点的边上的信息素进行更新。

算法伪代码如下：

procedure AS

for each edge

set initial pheromone value to

end of

while not stop

for each ant m

randomly choose an initial vertex

for i-l to k

choose next vertex with probability

end for

end for

compute the length Lk of the path constructed by the mth ant

for each edge

update the preromone value

end for

end while

print result

end procedure

蚁群算法对排考过程中的考试时间安排，提供了台理的考试时间安排表，解决了时间和教室冲突问题。

3.2 考场安排算法

学校的教室一般座位数固定不变，依据功能分为多媒体教室、普通教室、实验室等，根据各门课程考试要求，例如英语课程考试要求教室具有听力设备，安排相应合理的教室进行考试。同时，还要依据选修课程的学生数安排具有相近数量座位的教室进行考试。

考场安排算法大致步骤如下：

（l）判断课程有无特殊要求，为其安排合理的教室。

（2）依据选修课程的学生人数，教室的座位数量（教室的座位数量>选修课程学生人数）为其安排考场。

（3）若学生人数大于最大教室的座位数量，则应该依据考生人数安排相应数量的教室。

3.3 监考教师安排算法

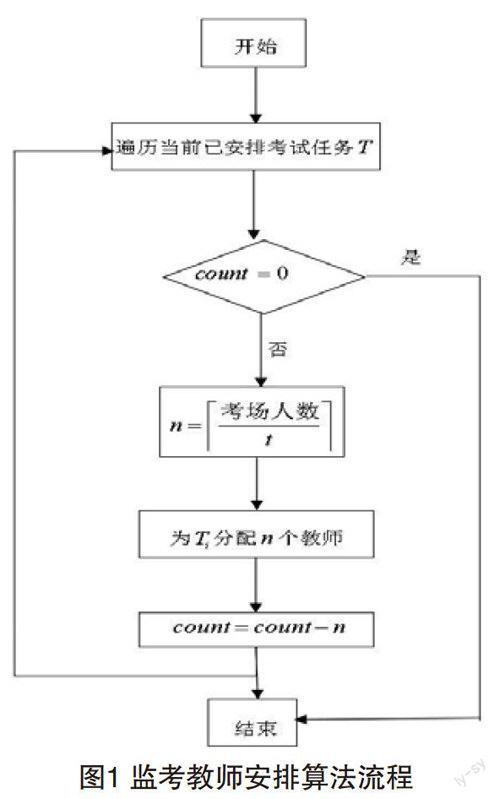
根据3.1考试时间安排算法以及3.2考场安排算法，在监考教师安排算法的设计过程中构造一个循环队列R，存储教师的信息，且用count存放队列R中元素的个数。给已经分配考试时间以及考试地点的考试任务分配监考教师，判断考场的考试人数，读取预先设定参数t（多少学生分配一个监考老师）分配监考老师，本文设t=15。如果需要监考老师n人，就从循环队列中读取n个教师分配给这个考试任务以尽量增大监考的间隔。

按照监考编排算法的描述过程，算法流程如图l所示。

该算法完成对考试任务进行监考教师的安排。

4 结语

本文针对高校教务管理中的排考资源冲突问题进行优化，采用蚁群算法对考试时间进行安排；根据考试时间安排和考场安排算法得出已经分配考试时间以及考试地点的考试任务，又利用监考安排算法对考试任务进行监考教师的安排，从而完成排考过程。解决了排考在时间、监考教师及考场资源之间的冲突问题，为高校的教学工作得顺利进行提供了便捷。