超厚滑坡稳定性数值分析

王秀丽,陈美合,于光明

(1.兰州理工大学 土木工程学院,甘肃 兰州　730050;

2.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州　730050)



超厚滑坡稳定性数值分析

王秀丽1,2,陈美合1,2,于光明1,2

(1.兰州理工大学 土木工程学院,甘肃 兰州730050;

2.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州730050)

摘要以锁儿头滑坡工程为背景,探讨其稳定性,并研究滑带土的摩擦角及内聚力对超厚滑坡安全系数的影响。结果表明:采用强度折减法计算安全系数与采用不平衡推力法的计算结果基本一致,二者误差不超过5%,说明所建立H0-2-2滑坡数值分析模型是可靠的;滑坡后壁局部滑塌,与实际勘测结果一致;滑坡属于推移式滑动,发生剪切破坏的潜在位置在滑坡体中段及后端;安全系数随着摩擦角及内聚力的增大而增大,摩擦角增大70%时,安全系数增大5.4%,内聚力增大70%时,安全系数增大10.7%,且后者对安全系数的影响比前者大。

关键词超厚滑坡;稳定性;安全系数;摩擦角;内聚力

边坡稳定性分析是岩土工程中的一个热点问题,正确分析边坡稳定性对确保人民生命财产安全具有重要意义。国内外的学者对边坡稳定性问题作了大量的研究工作。张晓咏等[1]应用ABAQUS程序进行渗流作用下边坡稳定分析;许江波等[2]应用FLAC3D分析弹性模量、时间间隔、局部阻尼系数的选取对土质及软岩边坡地震稳定性影响,提出一种全新的动力边坡稳定性判断方法;武科等[3]应用FLAC3D对坝体灌浆前后稳定性进行数值模拟分析;刘玉丽等[4]应用FLAC强度折减法分析边坡安全系数的影响因素;胡浩等[5]探讨了基于强度折减法的分层边坡安全系数影响因素;巨能攀等[6]用3DEC探讨岩质边坡块体失稳动态过程,分析块体之间的相互关系,确定关键块体,利用块体理论评价其稳定性,为治理设计提供依据;李忠等[7]对滑坡地带多级路堑边坡阶梯开挖三维数值模拟进行分析,但以上的研究是对浅层或中层边坡进行稳定性分析,而对超厚非均质边坡研究较少。现在前人研究的基础上,以锁儿头H0-2-2滑坡为背景,探讨超厚滑坡的稳定性,分析滑带土参数摩擦角及内聚力分别对超厚滑坡安全系数的影响,以期为研究超厚滑坡及更加准确地评价超厚滑坡的稳定性提供借鉴。

1基本原理

强度折减法中边坡稳定的安全系数定义为:使边坡刚好达到临界破坏状态时,对岩、土体的抗剪强度进行折减的程度,即定义安全系数为岩土体的实际抗剪强度与临界破坏时的折减后剪切强度的比值,其公式为

cF=c/Ftrial,

(1)

φF=tan-1((tanφ)/Ftrial),

(2)

其中:c为粘接力,单位(Pa);φ为摩擦角,单位(°);cF为折减后的粘接力,单位(Pa);φF为折减后的摩擦角,单位(°);Ftrial为折减系数。

利用式(1)、式(2)来调整岩土的强度指标φ和c,然后对边坡稳定性进行数值分析,通过不断增加折减系数,反复计算,直至达到临界破坏,此时得到的折减系数即为安全系数Fs[8]。

强度折减法的关键问题是临界破坏状态的确定,即如何定义失稳判据。现行强度折减法判断失稳破坏的标准有[9]:①迭代求解过程不收敛。该判据认为非线性有限元计算时,在给定求解迭代次数及收敛标准内未收敛则认为边坡失稳;②塑性区的连通状态。边坡变形过程总伴随着一些物理量出现和发展,当这些物理量达到一定值时则认为边坡失稳;③以特征部位位移突变性来认定边坡的稳定性。目前,位移失稳判据一般方法是建立每次有限元计算的某个部位位移或者最大位移与折减系数关系曲线,以曲线上的轨点作为边坡处于临界破坏状态的判据。

2工程概况

锁儿头滑坡属多层、多级巨型断层破碎带滑坡,长期处于缓慢蠕滑状态,稳定性差,具有多期次及分级性,由于规模大,各段地形及地层岩性差异较大,导致各段变形破坏模式及变形机理存在差异。锁儿头滑坡全长3 300 m,滑坡宽80~700 m,总面积约126×104m2,主滑方向133°,堆积体厚度20~100 m,体积7 286×104m3,其外围共发育大小滑坡10个,崩塌2个,主要研究滑坡前缘东侧H0-2-2滑坡,滑体最大厚度90 m,平均厚度60 m左右,属于超厚滑坡,该滑坡只有一个老的深滑面,埋深60~70 m,滑带为炭质板岩碎屑,滑体物质为碎石土,下层为炭质板岩碎屑,滑床为冲洪积碎石土,下伏炭质板岩基岩。基岩面埋深大、滑面埋深大、滑面坡降大、滑面以下的碎石土厚度也大。

现场的勘探及定性定量分析结果表明锁儿头滑坡在现状条件下局部处于蠕滑变形阶段,H0-2-2滑坡后壁局部滑塌,前缘公路挡土墙变形严重,新修公路挤压破坏,坡面出现断续纵向裂缝,房屋出现裂缝,泉水出露,有大量的张拉裂缝,判定为稳定性差。前缘受江水侧蚀,滑塌变形剧烈,以牵引式滑塌为主。

3数值分析模型的建立

根据锁儿头滑坡地质平面图及滑坡主剖面(见图1),建立FLAC3D计算模型,见图2。对滑坡的地形做了相应简化,将滑坡体定义为由三种材料(基岩、滑带土及滑体)共同组成,长为1 120 m(X轴),宽为35 m(Y轴),最大高度为272 m(海拔1 514 m),划分单元2 735个,节点1 968个。计算时采用Mohr-Coulomb模型,仅考虑自重的作用,不考虑构造应力场。因此,模型的底面为固定约束,除坡面外,模型四周边界设置为单向约束边界。

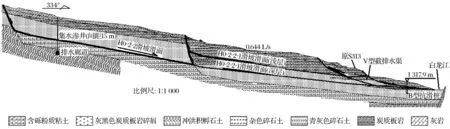
图1　H0-2-2滑坡计算剖面简图Fig.1　Sketch of landslide rated section by H0-2-2

FLAC3D计算模型中各岩土体物理力学参数取值见表1。

4计算结果及分析

4.1计算结果

由强度折减法所计算出来的H0-2-2滑坡安全系数为1.164,与勘察设计采用不平衡推力法即传递系数法计算出来的1.111误差不超过5%,可充分说明图2建立的H0-2-2滑坡数值分析模型是可靠的。H0-2-2滑坡在天然状态下应力分布如图3所示,其特点与天然斜坡应力基本相符,最大主应力自地表向坡体内部岩层深处逐步增大。越靠近表层最大主应力越小,与坡面越接近平行,最大主应力随坡面起伏而变化,受滑坡坡度及岩性影响。坡体最小主应力如图4所示,其分布规律和最大主应力分布有所相似。

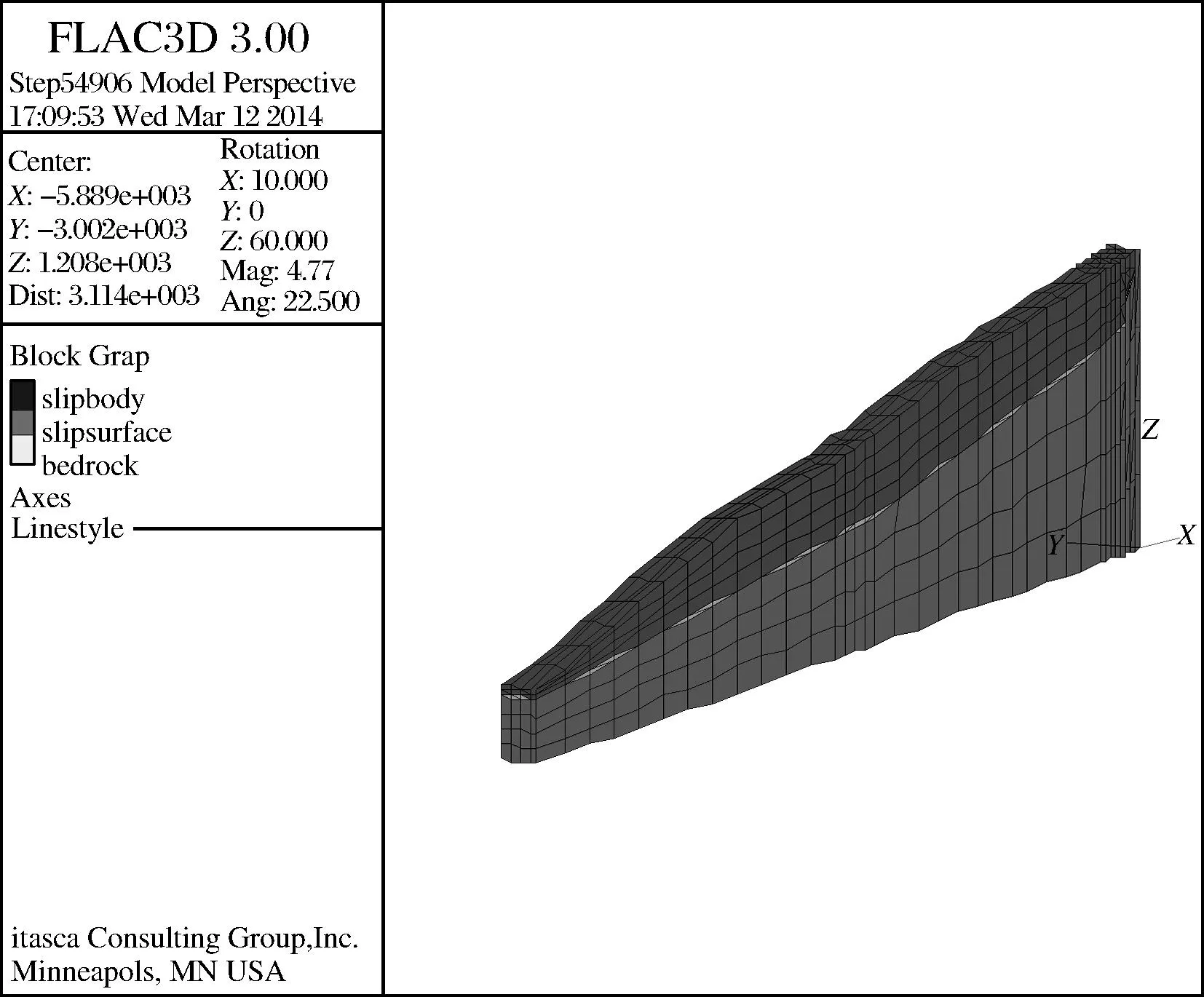
图2　H0-2-2计算模型Fig.2　H0-2-2 calculation model

岩性项目重度γ/(MN·m-3)变形模量E/(kN·m-2)泊松比υ内聚力c/kPa摩擦角φ/(°)基岩0.0223.2E90.2015039滑体0.0203.7E60.292820滑面0.01853.7E60.3510.215

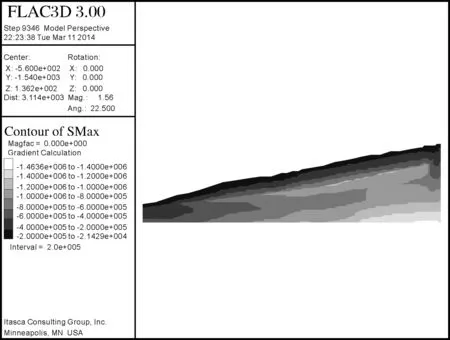
图3　坡体最大主应力分布云图Fig.3　Distribution nephogram of slopemaximum principal stress

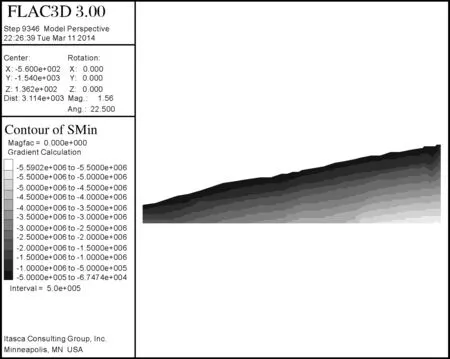
图4　坡体最小主应力分布云图Fig.4　Distribution nephogram of slopeminimum principal stress

剪应力增量如图5所示。主要集中在滑坡体中段及后端,没有贯穿整个滑面,呈现出中部向前段延伸的趋势。说明H0-2-2滑坡发生剪切破坏的潜在位置在滑坡体中段及后端,从中部向前段不断延伸。对H0-2-2滑坡进行治理时可以优先选择对滑坡中段及后端进行加固,而不是滑坡的前缘(见图6)。

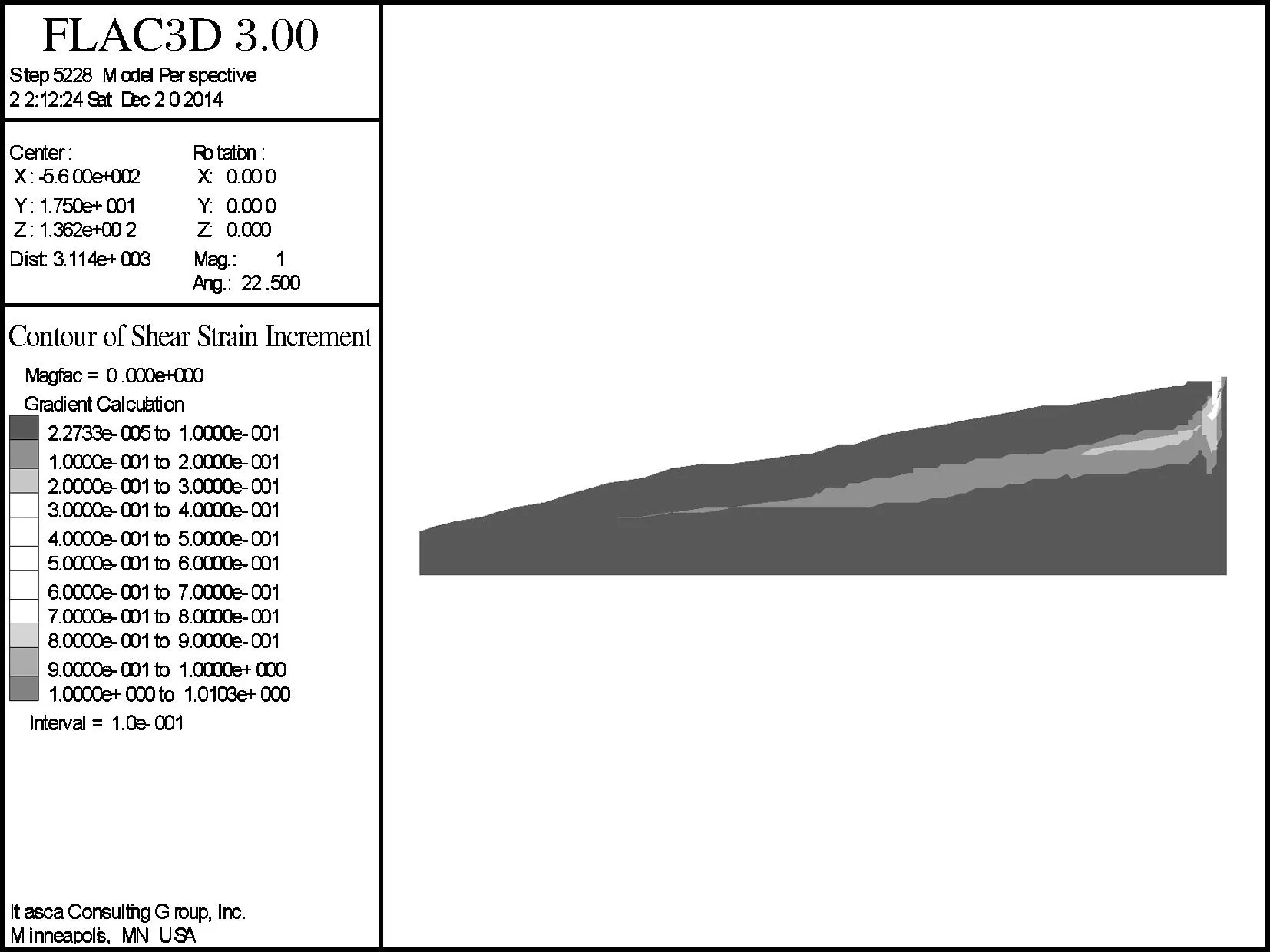
图5　剪应力增量Fig.5　Increment graph of shearing strength

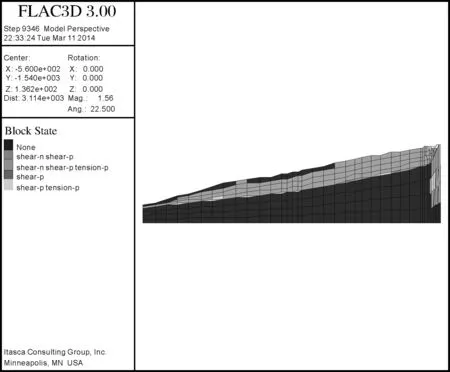
图6塑性区分布Fig.6　Distribution of plastic zone

滑坡后缘的位移量最大达到1.00~1.88 m(见图7),变形由后缘向下段不断递减,说明滑坡主要是推移式滑动,与现场勘测结果一致。

4.2敏感因素分析

定量评价滑坡稳定性时,滑带土的抗剪强度参数是必须的重要参数[10]。然而,有时摩擦角相差1°～2°,推力会成倍增加,其主要原因是土介质的多样性,成分、成因和结构的复杂性与不均匀性以及外界的多变性,使得用仪器的试验方法很难准确确定滑带土的实际受力状态。

图7　位移分布特征Fig.7　Diagram of displacement distribution features

锁儿头滑坡规模巨大,滑坡区山大沟深,地形破碎,岩土体结构变化大,分布不均匀,物理力学性质差异极大,能否准确分析滑坡稳定性,滑带土内聚力c及摩擦角φ的取值是关键因素。为此,根据实际情况对锁儿头滑坡对滑带土内聚力c及摩擦角φ进行单因素分析,改变其中一个参数时,其他参数不变。

滑带土体内聚力、摩擦角与安全系数的关系见图8。图8中横坐标为相应参数在原计算参数上增长的比例。由图8可知,边坡安全系数随着抗剪强度参数的增大而增大,内聚力的斜率明显比摩擦角的大,当摩擦角增大70%时,安全系数从1.164增大到1.227,增加了5.4%,内聚力增大70%时,安全系数从1.164增大到1.289,增加了10.7%,且内聚力对安全系数的影响比摩擦角大。

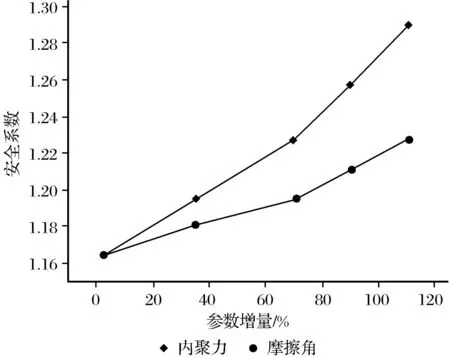
图8　内聚力、摩擦角与安全系数关系Fig.8　Relational graph of cohesion, fractionangle and safety factor

因此,在进行滑带土内聚力c及摩擦角φ取值时,需要弄清楚滑坡地质条件、类型、机理、滑带土的成因、结构、状态、影响的强度因素及变化趋势、变化的规律,以及滑坡运动状态之后,综合选取比较符合的取值,否则计算出来的安全系数和实际情况会有较大差异。

5结论

(1)由强度折减法所计算出来的滑坡安全系数为1.164,与勘察设计采用不平衡推力法即传递系数法计算出来的1.111误差不超过5%,充分说明已建立H0-2-2滑坡的数值分析模型是可靠的。

(2)剪应力增量主要集中在滑坡体中段及后端,没有贯穿整个滑面,呈现出中部向前段延伸的趋势。说明H0-2-2滑坡发生剪切破坏的潜在位置在滑坡体中段及后端,从中部向前段不断延伸。对H0-2-2滑坡进行治理时可以优先选择对滑坡中段及后端进行加固,而不是滑坡的前缘。

(3)滑坡在滑动过程中发生剪切拉张破坏位置与实际勘察结果基本一致,滑坡后缘的位移量最大,达到1.00~1.88 m,变形由后缘向下段不断递减,说明滑坡主要是推移式滑动,与现场勘测结果一致。

(4)边坡安全系数随着滑带土抗剪强度参数的增大而增大,当摩擦角增大70%时,安全系数从1.164增大到1.227,增加了5.4%,当内聚力增大70%时,安全系数从1.164增大到1.289,增加了10.7%,且内聚力对安全系数的影响比摩擦角大。

参考文献:

[1]张晓咏,戴自航.应用ABAQUS程序进行渗流作用下边坡稳定分析[J].岩石力学与工程学报,2010,29(S1):2 927-2 934.

[2]许江波,郑颖人,叶海林.土质及软岩边坡地震稳定性影响因素分析[J].地下空间与工程学报,2011,7(6):1 233-1 240.

[3]武科,马秀媛,赵青.FLAC~(3D)在土坝劈裂灌浆防渗稳定性分析中的应用[J].岩土力学,2005,26(3):484-487.

[4]刘玉丽,刘海波,林大超,等.FLAC强度折减法确定边坡安全系数的影响因素分析[J].河南大学学报:自然科学版,2011,41(3):323-326.

[5]胡浩,刘正才.基于强度折减法的边坡安全系数影响因素分析[J].长沙大学学报,2012,26(2):21-23.

[6]巨能攀,赵建军,黄润秋,等.基于3DEC的边坡块体稳定性分析[J].辽宁工程技术大学学报:自然科学版,2009,28(6):925-928.

[7]李忠,杨俊,曹永春.滑坡地带多级路堑边坡阶梯开挖三维数值模拟[J].甘肃科学学报,2014,26(6):116-120.

[8]陈育民,徐鼎平.FLAC及FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2009.

[9]吕擎峰.土坡稳定分析方法研究[D].南京:河海大学,2005.

[10]戴自航,张晓咏.滑带土抗剪强度指标反算的有限元方法[J].铁道科学与工程学报,2009,31(2):28-33.

Numerical Analysis of Stability of Super-thick Landslide

Wang Xiuli1,2,Chen Meihe1,2,Yu Guangming1,2

(1.CollegeofCivilEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China;2.WesternCenterofDisasterMitigationinCivilEngineeringofMinistryofEducation,Lanzhou730050,China)

AbstractAgainst the background of Suoertou landslide project,this paper discussed its stability,and studied the impact of friction angle and cohesion of slide zone soil on the safety factor of super-thick landslide.Research results showed that:the safety factors that respectively calculated with strength reduction method and imbalance thrust force method are basically consistent,with an error less than 5%,indicating that the established H0-2-2 landslide numerical analysis model is reliable;the back scarp locally slumps,and this is consistent with the actual survey results;the landslide belongs to push-type sliding,so the potential area of shear failure is in the middle and rear part of the landslide mass;the safety factor increases with the increasing of friction angle and cohesion,with 70% increase of friction angle leading to a 5.4% increase of safety factor,and a 70% increase of cohesion leading to a 10.7% increase of safety factor,and the latter has a large impact on safety factor than the former.

Key wordsSuper-thick landslide;Stability;Safety factor;Fraction angle;Cohesion

中图分类号:TU44

文献标志码:A

文章编号:1004-0366(2016)01-0083-05

作者简介:王秀丽(1963-),女,辽宁沈阳人,教授,博导,研究方向为大跨度空间结构及滑坡泥石流防治.E-mail:chenmeihe.1988@163.com.

基金项目:“十二五”国家科技支撑计划项目(2011BAK12B07).

收稿日期:2014-12-11;修回日期:2015-02-23.

doi:10.16468/j.cnki.issn1004-0366.2016.01.019.

引用格式:Wang Xiuli,Chen Meihe,Yu Guangming.Numerical Analysis of Stability of Super-thick Landslide[J].Journal of Gansu Sciences,2016,28(1):83-87.[王秀丽,陈美合,于光明.超厚滑坡稳定性数值分析[J].甘肃科学学报,2016,28(1):83-87.]