多盘转子系统动力学研究

胡四辈,梁　瑞,郑运虎

(1.兰州理工大学 石油化工学院,甘肃 兰州　730050;

2.兰州石化石油化工厂 ,甘肃 兰州　730060)



多盘转子系统动力学研究

胡四辈1,2,梁瑞1,郑运虎1

(1.兰州理工大学 石油化工学院,甘肃 兰州730050;

2.兰州石化石油化工厂 ,甘肃 兰州730060)

摘要航空汽轮机、水泵、风机、压缩机、膨胀机、电机等高速旋转机械,在运行时通常要考虑转子系统的一阶临界转速问题,有的甚至要考虑二阶、三阶以上的临界转速,以防止共振破坏的发生。转子动力学作为一门独立的学科,其发展和应用始终受到科研和生产单位的重视。为研究转子系统动力学特性,以多盘转子为例,介绍了转子动力学的相关内容,通过采用Workbench软件计算出了转子模态与对应临界转速、米塞斯等效应力和相应振型,并根据计算结果分析了转子的强度,对多盘转子系统动力学的研究、转子结构的优化设计和实际工程应用起到一定的指导作用。

关键词转子;动力学;振型;临界转速;应力

转子的临界转速是设计人员和实际操作人员必须考虑的关键问题,如果转子的转速接近临界转速会导致剧烈的振动或共振现象的发生。在转子剧烈振动的情况下,如果振幅过大会导致应力集中,造成过大的二次应力,使结构发生破坏。国内外专家学者对此做过大量研究工作。李朝峰等[1]采用有限元法建立双转子轴承系统动力学模型,并计算分析了轴承刚度与内外转子的转速比对临界转速的影响;邓四二等[2]建立了含轴承的动力学方程,分析了轴承结构参数对转子动力学的关系;翟黎明等[3]采用SAMCEF ROTOR程序建立发电机转子-轴承三维有限元模型,研究系统在不平横拉力刚度系数作用下临界转速和振型;罗火贵等[4]通过简非线性轴承刚度的模型,研究反向旋转机构的振动特性;Gupta等[5]采用矩阵算法计算转子的振型、临界转速和外界激励载荷;Nelson等[6]考虑了陀螺效应对转子动力学的影响,并采取了有限元法进行了数值模拟;Ferraris等[7]建立了刚度不对称的反向旋转结构的有限元模型,并分析了转子的模态和临界转速问题。Rao等[8]采用有限元法分析了三转子结构的动力学行为,得出结构前六阶固有频率下的不同振型和临界转速。我们采用Workbench对多盘转子的动力学进行了数值模拟,提前了前六阶固有频率,并对前六阶固有频率对应的振型、临界转速和共振发生时分别对应的等效应力值进行了计算和分析,研究结构发生破坏时最大形变和应力情况。

1动力学理论基础

模态分析[9]是动力学分析的基础,常用的模态分析方法有:子空间迭代法、变换技术求解非对称法、阻尼法、缩减法或凝聚法、QR阻尼法和分块兰索斯法,通常默认的为分块兰索斯法。

由经典力学理论可知,物体的动力学通用方程为[9-11]

,

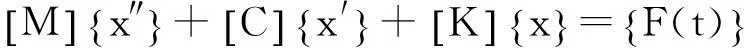
(1)

其中:[M]是质量矩阵;[C]是阻尼矩阵;[K]是刚度矩阵;{x}是位移;{F(t)}是力矢量;{x′}是速度矢量;{x″}是加速度矢量。无阻尼模态分析是经典的特征值问题,但是这里旋转机械具有特殊性:计算时需要考虑旋转软化和陀螺效应的影响,因此式(1)中的阻尼矩阵和刚度矩阵必须考虑为转速的函数。最后总临界转速归结为复合特征值的形式:

-(ω2M+iωB(x)+K(x))q=0,

(2)

其中:ω为系统临界频率;i为矩阵特征值。

2有限元计算

2.1模型及参数

主轴公称直径90 mm,总长1 500 mm,材料为高强度合金钢,弹性模量为2.12E11 Pa,密度为7 850 kg/m3,屈服强度为780 MPa,抗拉强度为960 MPa;轴承1距左端面50 mm,轴承2距左端580 mm,轴承3距离右端50 mm;盘1直径为300 mm,厚30 mm,距轴左端面200 mm;盘2直径为550 mm,厚30 mm,距离主轴左端面680 mm;盘3直径为200 mm,厚20 mm,距主轴右端面315 mm,模型见图1。转子材料为结构钢,弹性模量为2.11E11 Pa,泊松比为0.32;密度为7 850 kg/m3;采用ICEMCFD划分六面体网格,网格划分结果为142 346个节点,34 169个单元。网格划分情况见图2。在图1中的轴承位置分别设置各轴承的刚度和阻尼,轴承1、轴承2和轴承3的刚度与阻尼参数见表1。将转子的轴线位移设为0,径向和切线位移设为自由约束。设定转子的转速为6 000 rad/s,取数据点数为6,在每个数据点设置对应的转速,为便于计算收敛,转速应从小到大按顺序设定。在后处理中设定需要输出的形变、应力和坎贝尔图等选项。设置完成开设求解。

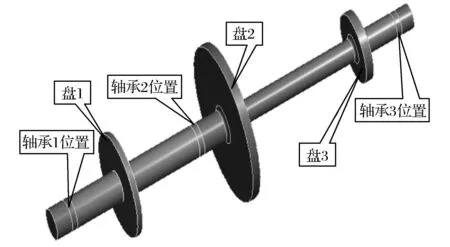
图1　转子模型Fig.1　Rotor model

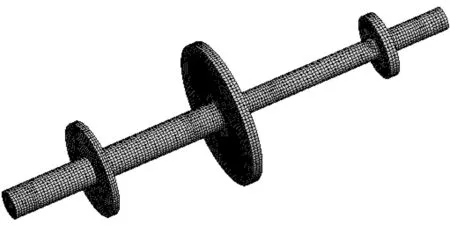
图2　网格划分结果Fig.2　Result of grid division

轴承Kx/(N·mm-1)Ky/(N·mm-1)Cx/(N·S·m-1)Cy/(N·S·m-1)11e81e810010021.3e81.3e812012031.6e81.6e8150150

2.2计算结果与分析

在后处理模块中插入软件的Deformation和Mises equivalent stress求解模块后分别得到图3~图8的前六阶固有频率对应的振型云图和图9~图14前六阶振型下的应力云图。

图3与图4分别是XY平面内X、Y两向对应的第一、二阶振型云图,可以看出第一、二两阶的振型以弯振为主,最大振幅都集中在第二转盘和第三转盘的轴段上,并且最大位移值相等,第盘和第三第二转盘轴段振幅较小,弯曲程度较第二和第三转盘之间的要弱;第三阶振型以轴径向的胀缩为主,最大振幅集中在第三转盘的径向上,转盘外环面最大形变为13.735 mm,其次为第三转盘的外盘面的轴段上。第四阶和第五阶振型仍然以弯振为主,最大振幅靠近第三转盘,最大形变为5.9 mm。第六阶振型以径向的胀缩为主,最大形变位于第一转盘的外环面上,其次为第一转盘外盘面的轴段上。

图3　第一阶振型云图Fig.3　Shape counter for first model

图4　第二阶振型云图Fig.4　Shape counter for secomd model

图5　第三阶振型云图Fig.5　Shape counter for third model

图6　第四阶振型云图Fig.6　Shape comter for fourth model

图7　第五阶振型云图Fig.7　Shape counter for fifth　model

图8　第六阶振型云图Fig.8　Shape counter for sixth model

图9　第一阶振型下应力云图Fig.9　Stress counter for first model

图10　第二阶振型下应力云图Fig.10　Stress counter for second model

图11　第三阶振型下应力云图Fig.11　Stress counter for third model

图12　第四阶振型下应力云图Fig.12　Stress counter for fourth model

图13　第五阶振型下应力云图Fig.13　Stress counter for fifth model

图14　第六阶振型下应力云图 Fig.14　Stress counter for sixth model

一阶振型下最大应力位于轴承2的内圈与轴接触的位置,应力值达到了718 MPa,接近材料的屈服强度。如果外界激励载荷频率达到结构的一阶固有频率时,结构应力值会增大,接近轴的屈服强度。二阶振型下对应的最大应力为593 MPa,最大应力集中与第二转盘和第三转盘之间的轴段上。图11为第三阶振型下的应力云图,最大应力值为1 553 MPa,最大应力位于转盘2外盘面与轴接触的位置,超过了结构的屈服强度和抗拉强度,即当外界激励载荷频率阶级三阶固有频率时,结构会发生共振,结构可能会发生断裂。第四阶振型下结构对应的最大应力为2 231 MPa,集中在转盘2外盘面与轴装配的位置,该应力远远超出了结构的抗拉强度,若外界载荷频率接近四阶固有频率,那么结构将发生断裂破坏。同样,第五阶振型下的最大应力值也集中在第二转盘外盘面与轴配合的位置,当外界激励载荷接近五阶固有频率时,结构会发生断裂破坏。第六阶振型下的最大应力位移转盘2的内盘面与轴配合的位置上,应力值达到了1 716 MPa,同样超出了许多应力值,当外界激励载荷接近六阶固有频率时,结构将发生断裂破坏。

2.3坎贝尔图

坎贝尔图是一种判断转子工作时是否出现共振的频率阶次、共振转速的工程解法。横坐标表示共振转速、纵坐标表示固有频率。坎贝尔图的临界转速针对的是旋转机械,可以帮助工程人员优化设计,提高设计效率并指导工程的实际操作,有效避免共振的问题。图15即为多盘转子的坎贝尔图,该图为ANSYS后处理计算结果的截图,图15中的黑色三角区表示前六阶固有频率所对应的临界转速值。在Workbench的后处理输出数据中可以得到各固有频率依次对应的临界转速为1 087.5 rad/s、1 684.1 rad/s、2 465.8 rad/s、2 337.7 rad/s、0和2 996 rad/s。这里需要解释第五阶固有频率下对应的临界转速为0的问题,从图15可以看出临界转速与第五阶固有频率没有交线,而其他固有频率都有临界转速交点,因此这里的0表示的是第五阶固有频率在0~6 000 rad/s的转速范围内,临界转速不存在。

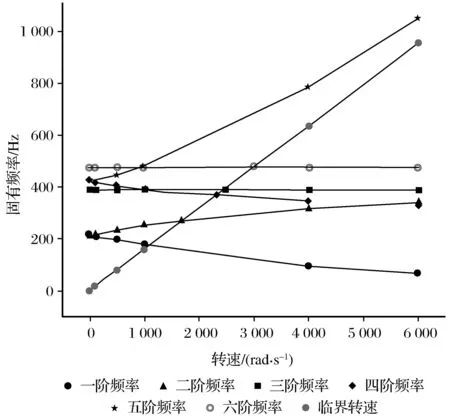
图15　转子临界转速坎贝尔图 Fig.15　Campbell chart of critical revolving speed of rotor

3结论

(1) 通过对多盘转子结构动力学的数值模拟,为转子结构的优化设计和转子临界转速的计算提供了一种软件计算方法。

(2) 根据有限元软件计算结果,对实际工况的控制起到一定的指导作用,坎贝尔图的计算结果对避免旋转结构因临界转速而发生共振破坏起到一定的参考作用。

(3)模态分析结果表明轴承的刚度和阻尼等参数对系统的共振现象有很大影响,提高轴承刚度和结构刚度在一定意义上都可以避免低频共振的现象。

(4) 各振型对应条件下的应力数值表明,固有频率的大小与结构共振时的应力值之间不存在线性关系,即低频率共振时的最大应力可能大于高频共振时的最大应力。

(5) 振型和应力分析结果表明旋转轴的各轴段直径过渡不能太大,防止共振时振幅过大和应力过于集中导致结构破坏。

参考文献:

[1]李朝峰,刘广超,周世华,等.双转子多盘转子系统的动态特性[J].东北大学学报:自然科学版,2013,59(7):994-998,1 004.

[2]邓四二,贺凤祥,杨海生,等.航空发动机双转子-滚动轴承耦合系统的动力特性分析[J].航空动力学报,2010,25(10):2 386-2 395.

[3]翟黎明,姚泽,黄青松,等.蓄能机组转子系统三维动力特性研究[J].农业机械学报,2014,58(9):107-111,137.

[4]罗贵火,胡绚,杨喜关.反向旋转双转子系统非线性分析[J].振动工程学报,2009,23(3):268-273.

[5]Gupta K,Gupta D Athre K.Unbalance Response of Dual Rotor System Theory and Experiment[J].Journal of Vibration and Acoustics,1993,115(4):427-435.

[6]Nelson H D.A Finite Rotating Shaft Element Using Timoshenko Beam Theory[J].Journal of Sound and Vibration,1980,102(4):793-803.

[7]Ferraris G,Maisonneuve V,Lalanne M. Prediction of the Dynamic Behavior of Nonsymmetriccoaxial Shape Counter Rotating Rotos[J].Journal of Sound and Vibration,1996,195(4):649-666.

[8]Rao J S,Sreenivas R.Dynamic of a Three Level Rotor System Using Solid Elements[C]//ASME Conference Proceedings.Atlanta,2003:601-606.

[9]赵万勇,王磊,白双宝.大型离心泵转子动力学分析[J].甘肃科学学报,2013,25(1):81-84.

[10]张洪才.ANSYS14.0理论机械与工程应用实例[M].北京:机械工业版社,2012.

[11]贾锐,石秀华,徐宇明,等.基于ANSYS的圆柱薄壳结构模态分析[J].弹箭与制导学报,2008,29(6):314-316.

[12]曹银萍,石秀华.基于ANSYS的鱼雷有限元建模与模态分析[J].弹箭与制导学报,2009,30(3):289-292.

Study on Dynamics of Multi-disc Rotor System

Hu Sibei1,2,Liang Rui1,Zheng Yunhu1

(1.CollegeofPetrochemicalEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China;2.LanzhouPetrochemicalandSinopecPlant,Lanzhou730060,China)

AbstractFirst-order critical revolving speed,or even second-order,third-order and above critical revolving speed of the rotor system shall be taken into account during rotating the machinery at high speed,such as aircraft gas turbine,water pump,the fan,the compressor,the expander,the motor,etc.In order to avoid occurrence of damage as a result of resonance. The research and development institution and the production unit always pay attention to development and application of the Rotor Dynamics as an independent subject. Moreover,the article,taking the multi-disc rotor as example,introduced relevant content of Rotor Dynamics and analyzed the strength of the rotor according to calculation result while calculating the rotor modal and corresponding critical revolving speed,as well as Mises stress and corresponding mode of vibration in order to research the dynamic characteristics of the rotor system. Furthermore,the above-mentioned research provides guidance for dynamic study of multi-disc rotor system,optimization of design of the rotor structure and application in the actual engineering.

Key wordsRotor;Dynamics;Mode of vibration;Critical revolving speed;Stress

中图分类号:TH311

文献标志码:A

文章编号:1004-0366(2016)01-0110-05

作者简介:胡四辈(1978-),男,甘肃兰州人,硕士,工程师,研究方向为石油化工安全管理.E-mail:921238461@qq.com.

基金项目:国家质检公益项目(201210026，201310152);甘肃省高等学校基本科研业务费(1205ZTC067).

收稿日期:2014-12-18;修回日期:2015-03-28.

doi:10.16468/j.cnki.issn1004-0366.2016.01.024.

引用格式:Hu Sibei,Liang Rui,Zheng Yunhu.Study on Dynamics of Multi-disc Rotor System[J].Journal of Gansu Sciences,2016,28(1):110-114.[胡四辈,梁瑞,郑运虎.多盘转子系统动力学研究[J].甘肃科学学报,2016,28(1):110-114.]