考虑投资努力的总承包工程建设利润分配模型

白振宇

（中油管道物资装备总公司，河北 廊坊 065000，E-mail：bazen868@163.com）



考虑投资努力的总承包工程建设利润分配模型

白振宇

（中油管道物资装备总公司，河北 廊坊 065000，E-mail：bazen868@163.com）

摘 要：以总承包工程建设中的总承包商和采办服务商为研究对象，考虑他们为获得更多的工程项目收益各自采取措施改善自身管理绩效实现节余项目预算资金。假设节余预算的比例为双方努力水平连续递增的凹函数，以收益共享理论和Stackelberg博弈思想为基础，建立总承包商和采办服务商的收益分配模型，分别研究了联合体情况下和分散决策情况下各自的最优决策问题，其中分散决策时分析得出项目预算节余资金在总承包商与采办服务商之间的最优分配比例，同时导出相关推论。通过算例分析了模型中各主要参数的变化对最优策略的影响来验证分析结果。

关键词：收益分配；投资努力程度；最优决策；节余预算分配比例

在工程总承包模式下，业主与总承包商签订承包合同，由总承包商负责管理和控制工程项目的进度、费用、质量、安全等，最终达到业主要求的项目目标。对总承包商来说，选择合适的项目管理模式，与各分包商建立长期的战略联盟伙伴关系，提高项目建设的总体协调能力、项目运作能力是总承包企业核心竞争力的体现。在当前项目建设招投标竞争日益激烈的情况下，总承包商必须设计合理的激励协调机制，充分调动工程总承包体制内分包商参与工程建设优化的积极性，为项目创造更多的收益，从而使总承包商和分包商获得更多收益。

国内外许多学者对工程建设中各参与方之间的激励协调问题进行了广泛的研究。一些学者认为可以通过设立激励契约对工程各参与方的决策行为进行诱导，来增强工程建设各参与方的积极性。国外学者Rose等[1]从业主角度，通过对澳大利亚4个工程项目业主与承包商之间激励因素选择的研究，得出业主对承包商增进关系激励的重要性高于对资金方面的激励。Peter等[2]根据对澳大利亚8个基础设施工程项目的29个工程参与者的调查内容，研究得出基础工程项目各参与者组成一个工程联合体时，风险或收益共享契约是工程成功的关键。Fani等[3]根据对42位专家的问卷调查结果指出参与者可以根据专家对高速公路项目选择标准的经验判断来确定具体的激励合同类型。国内学者主要就工程项目约定合同对项目参与者之间的收益协调进行研究。王安宇等[4]分别从一次性合作和重复合作两种情况研究了关系契约框架下研发联盟收益分配问题。管百海等[5]以合约理论和博弈思想为基础，研究了联合体工程总承包商的收益分配问题，得出了项目总承包收益在设计单位与施工企业之间的最优分配比例。尹红莲等[6]利用委托—代理理论，研究了总包与分包商一次性合作和长期合作下收益分配模型。张云等[7]通过构建总承包商和分包商供应链利润分配模型，得出为获得额外激励奖金二者的最大努力水平，以及之间的最优分配比例，并考虑他们之间能力差异对利润分配产生的影响。

工程项目的进度、成本、质量等工程目标伴随着工程建设的整个生命周期，而各工程目标之间相互联系又相互制约，对承包商各工程目标之间的均衡优化的研究以及承包商之间就某一个或多个工程目标如何激励协调的研究，是当前工程项目研究领域中的热点问题。Shr等[8]考虑工程周期与建设成本之间的关系，分别建立线性与非线性两种激励合同类型下的高速公路建设承包商决策模型，并通过实例验证模型的有效性。Afshar等[9]对于业主要求的工期、成本、质量多目标工程合同问题，建立了多目标优化均衡模型。伊长生等[10]根据可信性理论，建立了多模式工期、成本、质量均衡优化的模糊期望值模型。Zheng等[11]研究了工程项目工期—时间控制目标不同均衡状态下，业主与承包商的最优决策问题，分析认为项目业主和承包商的工程目标可由最低成本向缩短工期以及增加收益转变。

本文考虑总承包商与采办服务商分别投资加强自身项目管理以共同控制项目预算目标，基于收益共享和博弈论思想，分别从合作情形下及非合作情形下建立总承包商与采办服务商收益分配模型，并分别求出两种情形下的最优决策。

1 模型建立

1.1 问题描述

在工程建设总承包模式下，总承包企业集团内部往往成立施工、设计、采办专业化公司，并以企业集团或多企业联合形式参与某工程项目的投标工作，中标后把工程项目建设工作再分配给内部企业。这些专业化公司都是独立法人企业，都以盈利为目的，在集团内部相互之间是合作关系，但同时相互之间又是工程项目利润的争夺者。对工程项目目标，如工期、投资预算和工程质量、项目收益等进行控制是总承包内部企业之间协调决策的重点方面，因此研究总承包企业参与方的合作竞争关系具有重要的理论和现实意义。

为研究方便，把采办服务商从总承包企业内部分离出来，考虑采办服务商、总承包商共同投资努力控制预算，从最大化双方项目收益的角度，研究双方之间的合作竞争关系。实际工程项目建设中，采办服务商的收益一般包括采办服务费和采办预算节余分配资金，采办服务费费率往往由集团公司统一规定。项目开始时，总承包商会根据项目情况与采办服务商协商预算节余分配比例；采办服务商只要所获得的预算节余分配资金高于付出的投资努力成本，就会选择尽量提高投资努力水平改善采购管理来控制预算。

1.2 模型假设与建立

本文以总承包工程建设中的总承包商和采办服务商为研究对象，二者均为风险中性，联合投标某工程建设项目，假设投标总价由两部分组成：H=Q+P，其中Q为投资总预算，P为预期收益。

总承包商为控制项目预算获取更多的项目收益，一方面通过自身加强项目管理，比如努力优化施工路线、改善施工技术等，尽量降低工程预算；另一方面对采办服务商进行预算控制奖励，激励采办服务通过控制采购预算来努力控制项目总预算。采办服务商为获取更多的项目收益，只要总承包商提供的预算节余分配比例合适，就会努力减少采购预算，投资加强自身采办流程管理，提高采办人员素质，加强供应商管理，提高采办效率等。二者共同投资来努力降低项目预算资金，假设总承包商的投资努力程度为ξ1，采办服务商的投资努力程度为ξ2，通过投资努力总预算减少的比例为f(ξ1，ξ2)，为分别关于ξ1，ξ2的连续递增的凹函数，即f'(ξi)＞ 0，f ''(ξi)＜ 0；假设f( ξ1,ξ2)= 1 - e- αξ1- βξ2，其中α为总承包商的投资效率系数，β为采办服务商的投资效率系数。那么实际建设投资为Q0= [1 - f ( ξ1, ξ2)] Q，项目投资节余为f( ξ1, ξ2) Q。

项目建设前，采办服务商与总承包商约定采办服务费，作为采办服务商的收入，为采购物资总金额的某一比例，设采办服务费率为λ1，则采办服务费为λ1[1- f ( ξ1, ξ2)] Q 。在实际工程项目中，采办服务费率一般由集团公司、主管单位制定或根据国家法律制定（招标代理服务费管理暂行办法[计价格2002]）；工程项目的物资采购，往往分批分包进行采购，并分别与供货厂商签订合同，采办服务商对每个采购合同收取采办服务费，根据项目采办统计，工程总体的实际采办服务费率为1.5%左右。项目完成后，项目节余资金由总承包商与采办服务商进行分配，假设总承包商提供给采办服务商的分配比例为λ2，则总承包商的分配比例为1-λ2。一般的，采办服务费率远小于项目节余资金的分配比例，因为项目节余资金相对于工程总预算来说很少，实际项目节余资金的分配比例为40%左右。

为减少项目预算获取更多的项目收益，总承包商与采办服务商所进行的各种努力可以等价于货币成本即投资，随着努力程度的增加，相应的货币成本的增长速度会加快，则可假设总承包商或采办服务商的投资努力成本函数[7]表示为：

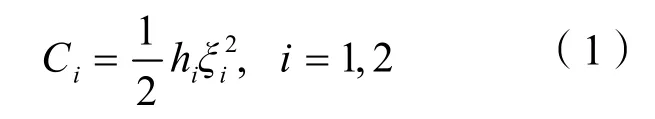
式中，h1，h2分别为总承包商、采办服务商的投资成本系数。

假设总承包商、采办服务商正常完成该工程项目所需成本为C01、C02为固定值。总承包商、采办服务商若看成统一的联合体，共同努力使联合体项目收益最大，假设I0为联合体情形下的总利润，则：分散决策下，总承包商与采办服务商各方单独进行投资，在考虑对方投资努力决策下，制定本方的最优决策。假设I1为总承包商的利润，I2为采办服务商的利润，Id为分散决策下二者总利润，则：

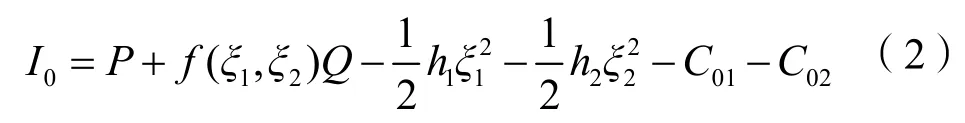
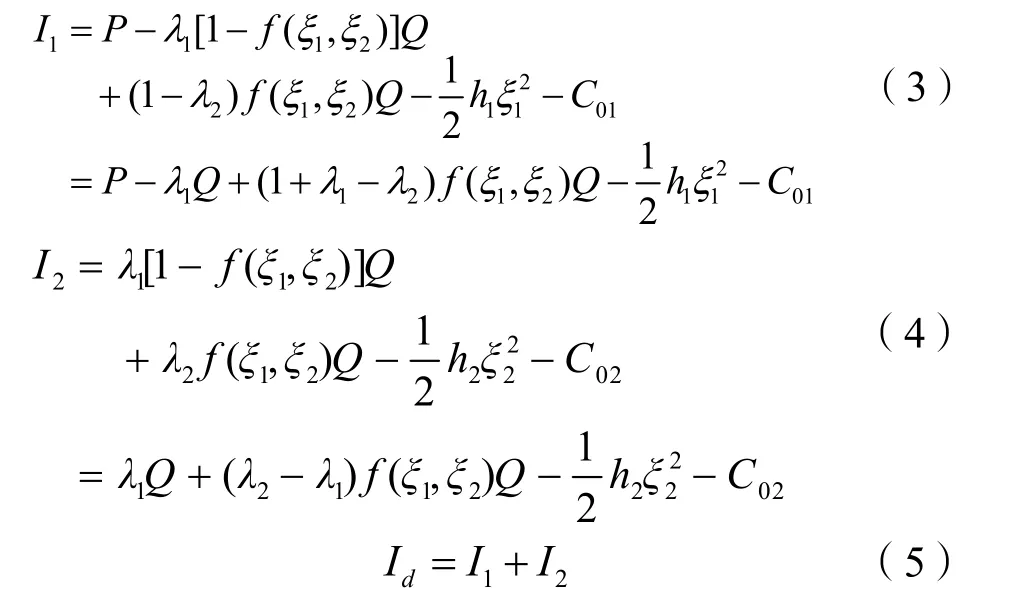
2 模型求解

2.1 联合体情形下

联合体情形下，把总承包商与采办服务商看成统一的整体，在信息完全共享的基础上考虑项目整体收益最大。即以联合体整体收益最大化为条件，确定总承包商与采办服务商的最优投资努力程度。

推论1：在联合体情形下，总承包商与采办服务商存在最优的投资努力水平使联合体总承包收益最大，且有。

证明：由式（2）可得联合体总利润关于ξ1，ξ2的二阶导数分别为：

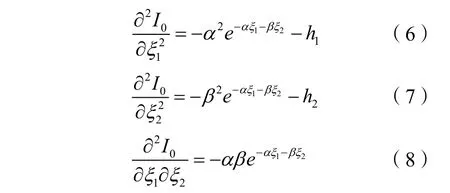
则Hessian阵：

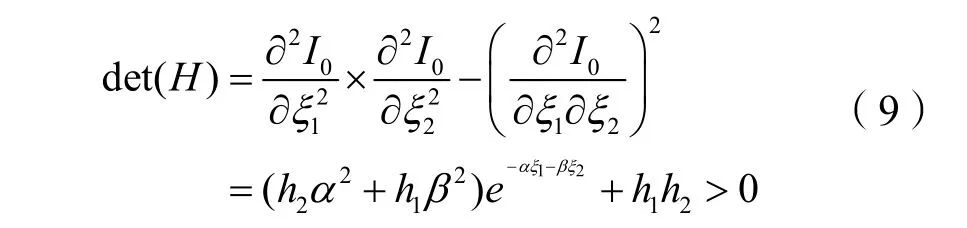
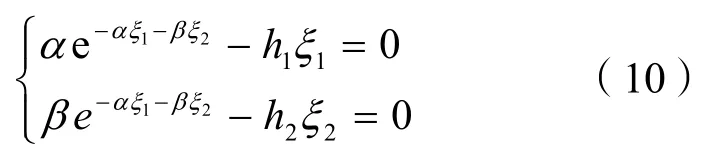
2.2 分散情形下

在分散情形下，总承包商、采办服务商独立决策，都以自身收益最大化为目标选择自身合适的投资努力水平。假设总承包商与采办服务商在项目开始前就已经协商好项目预算节余的分配比例，那么在工程建设过程中总承包商和采办服务商都会根据对方的决策来决定本方的行动，以使自身收益最大，即总承包商和采办服务商之间存在博弈关系。

推论2：在预算节余分配比例λ2确定的条件下，对于采办服务商任意给定的投资努力水平ξ2，总承包商存在最优的使其利润最大；反之，对于总承包商任意给定的投资努力水平ξ2，采办服务商存在最优的使其利润最大；均衡时、满足。

证明：总承包商的利润函数关于ξ1的一阶、二阶偏导数为：

采办服务商的利润函数关于ξ2的一阶、二阶偏导数为：

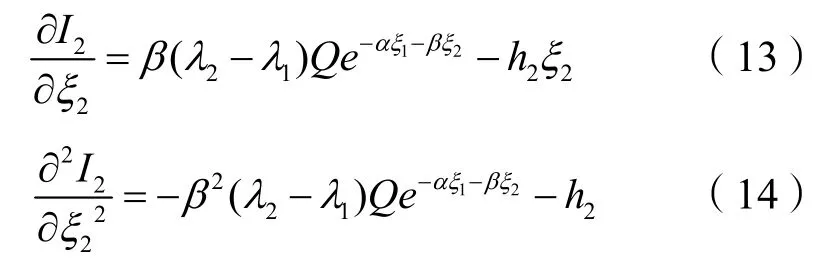
易知式（12）、式（14）均小于0，则在λ2确定的条件下，总承包商与采办服务商会根据对方的决策可以选择自身的行动使自身收益最大。

分散情形下，总承包商、采办服务商会根据对方行动选择自身行动，双方存在博弈关系，均衡点为双方利润函数一阶导数等于零处。

令∂I1/∂ξ1= 0，可求得总承包商从本方利润最大化的角度出发确定投资努力水平，即：

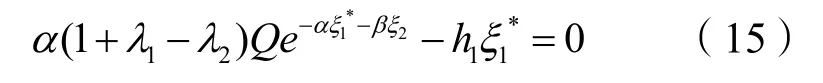
令∂I2/∂ ξ2= 0，可求得总承包商从本方利润最大化的角度出发确定投资努力水平，即：

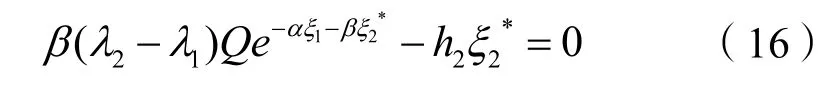
由式（15）、式（16）可得承包商和采办服务商利润最大点处的预算剩余分配比例为：

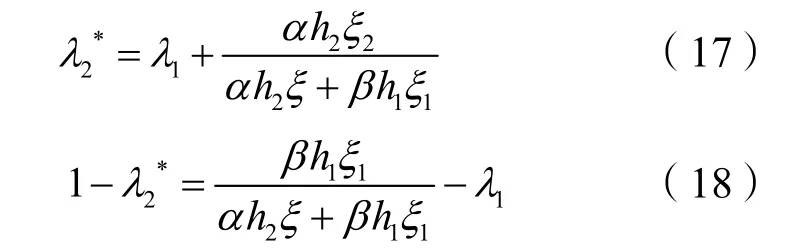
推论3：总承包商和采办服务商达到均衡时，各方的预算剩余分配比例与各方的投资效率系数成反比，与各方的投资努力水平及投资成本系数成正比。

3 算例分析

假设总承包商中标某工程项目，合同总金额为21200万元，其中投资总预算为20000万元，期望收益为1200万元，总承包商、采办服务商正常完成该项目的管理费用分别为300万元、100万元，采办服务商收取的采办服务费率为λ1=0.018，其他相关参数赋值借鉴张云等[7]数值算例的赋值情况，并根据模型求解特点调整得出：α=0.0015，β=0.0018，h1=0.8，h2=0.5。则计算可得：联合体情形下，总承包商最优投资努力程度、采办服务商最优投资努力程度和联合体最优总利润分别为=32.00，= 61.44，= 2379.79；分散决策下，总承包商和采办服务商各自最优投资努力程度及最优利润、最优采办资金节余分配比例、总利润分别为= 22.08，= 24.27，= 0.38，= 1285.39，= 651.02，=1285.39。可知，联合体情形下总承包商和采办服务商各自最优投资努力程度高于分散决策下各自的最优投资努力程度，联合体情形下总利润高于分散决策下的总利润。

（1）总承包商不同投资效率系数α对最优策略的影响，如表1所示。

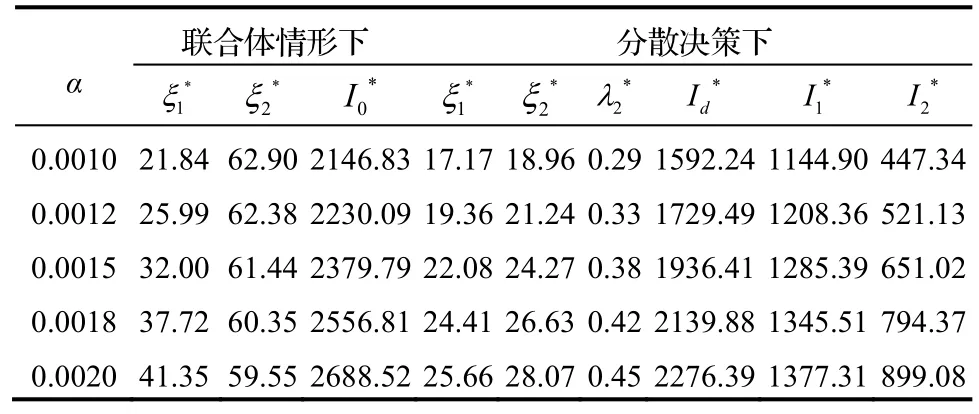
表1 不同投资效率系数α对最优策略的影响

由表1可知，联合体情形下，随着总承包商投资效率系数α增加，总承包商最优投资努力程度会随着增加，而采办服务商的最优投资努力程度会随着减小；意味着工程联合体从投资边际成本角度考虑，在一方投资效率增加进而增加投资努力程度的同时，另一方需减小投资成本以期整体利润提高。分散决策下，随着α的增加，总承包商和采办服务商各自的最优投资努力程度都会随着增加，表明总承包商为提高自身利润增加投资努力程度，会减少采购总额；而采办服务商同时为了提高自身利润增加投资努力程度换取增加节余资金分配比例。

（2）采办服务商不同投资效率系数β对最优策略的影响，如表2所示。

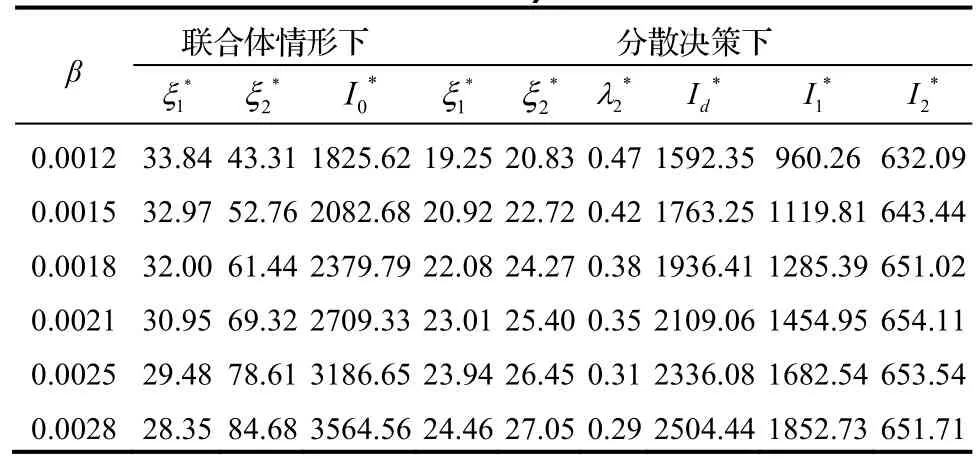
表2 不同投资效率系数β对最优策略的影响

由表2可知，联合体情形下，随着β的增加，总承包商最优投资努力程度会随着减小，采办服务商的最优投资努力程度会随着增加，联合体最优总利润也会随着增加。分散决策下，随着采办服务商投资效率系数的增加，总承包商和采办服务商各自的最优投资努力程度都会随着增加，而采办服务商最优节余资金分配比例会随着减小，采办服务商最优利润先增加后减少。表明分散决策下的总承包商处于主导地位，控制节余资金分配比例以使自身获利最大。

（3）总承包商不同投资成本系数h1对最优策略的影响，如表3所示。

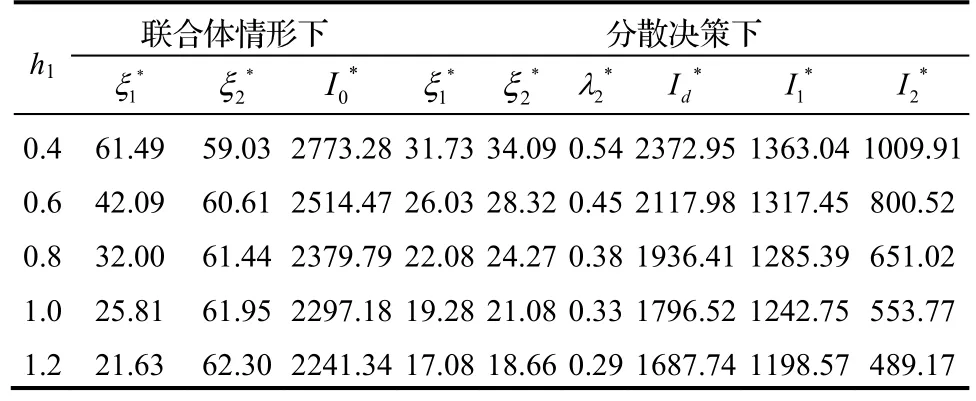
表3 不同投资成本系数h1对最优策略的影响

由表3可知，联合体情形下，当总承包商的投资成本系数h1增加时，总承包商的最优投资努力程度会随着减小，而采购服务商的最优投资努力程度会随着增加；总承包商的投资成本系数的增加，表明采购服务商的相对投资成本系数减小，为维护联合体总利润，采购服务商应增加投资。分散决策下，随着h1的增加，总承包商和采办服务商各自的最优投资努力程度都会随着减少，而最优节余资金分配比例也会随着减小，说明总承包商相对投资成本的增加，为维护其利润，控制采办服务商的节余资金分配比例。

（4）采办服务商不同投资成本系数h2对最优策略的影响，如表4所示。

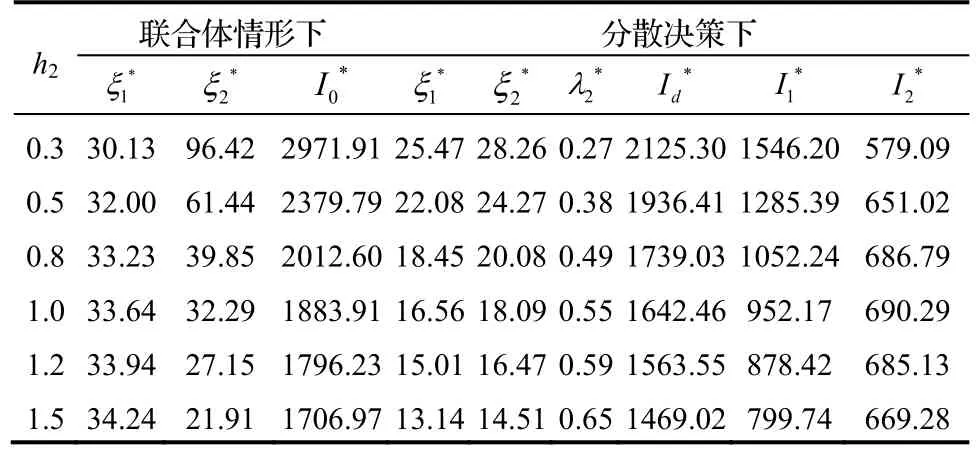
表4 不同投资成本系数h2对最优策略的影响

由表4可以看出，联合体情形下，当h2增加时，总承包商的最优投资努力程度会随着增加，采购服务商的最优投资努力程度会随着减小，原理与总承包商的投资成本系数h1增加类似。分散决策下，随着h2的增加，总承包商和采办服务商各自的最优投资努力程度都会随着减少，而最优节余资金分配比例会随着增加；意味着当采办服务商的相对投资成本增加时，会要求增加节余资金分配比例来维护自身利润。

4 结语

本文以总承包工程建设中的总承包商和采办服务商为研究对象，建立了总承包商与采办服务商的收益分配模型，分别研究了联合体情况下和分散决策情况下各自的最优决策问题，并通过数值算例给出了主要参数的灵敏度分析。

参考文献：

[1] Rose T，Manley K．Motivation toward financial incentive goals on construction projects[J]．Journal of Business Research，2011，64（7）：765-773．

[2] Peter E D L，Peter R D，Robert C．et al．Risk/Reward Compensation Model for Civil Engineering Infrastructure Alliance Projects[J]．Journal of construction engineering and management，2011，137（2）：127-136．

[3] Fani A，Georgios N A，Dimitrios K．et al．Selection Criteria Used for the Choice of Contract Type for Major Highway Construction Projects[J]．Procedia-Social and Behavioral Sciences，2012，48：3508-3517．

[4] 王安宇，司春林．基于关系契约的研发联盟收益分配问题[J]．东南大学学报（自然科学版），2007，4（37）：700-705．

[5] 管百海，胡 培．联合体工程总承包商的收益分配机制[J]．系统工程，2008，11（26）：94-98．

[6] 尹红莲，王卓甫，陈治义．工程总分包动态联盟收益分配研究[J]．人民长江，2009，5（40）：87-94．

[7] 张 云， 吕 萍，宋吟秋．总承包工程建设供应链利润分配模型研究[J]．中国管理科学，2011，4（19）：98-104．

[8] Shr J F，Chen W T．A method to determine minimum contract bids for incentive highway projects[J]．International Journal of Project Management，2003，21 （8）：601-615．

[9] Afshar A，Kaveh A，Shoghli O．Multi-objective optimization of time-costquality using multi-colony ant algorithm[J]．Asian Journal of Civil Engineering（Build and Housing）2007，8（2）：113-124．

[10] 伊长生，高建炳．基于模糊规划的工程项目工期—成本—质量均衡优化研究[J]．工程管理学报，2015，29 （1）：129-133．

[11] Zheng，D X，Ng S T and Kumaraswamy M M．Applying a Genetic Algorithm-Based Multi-objective Approach for Time-Cost Optimization[J]．Journal of Construction Engineering and Management，2004，130（2）：168-176．

白振宇（1986-），男，硕士，工程师，研究方向：工程项目管理，项目采购管理。

Profit Distribution Model of General Contracting Construction Considering Investment Degree

BAI Zhen-yu
（The China Petroleum Pipeline Material & Equipment Corporation，Langfang 065000，China，E-mail：bazen868@163.com）

Abstract：This paper sets up a profit distribution model between the general contractor and the procurement service provider assuming that they can reduce project cost to obtain profits by effective investment. By applying revenue sharing and Stackelberg game，the paper studies the optimal decision under the centralized situation and the decentralized situation respectively assuming that the reduced cost is one concave function with their investment degrees. And the best distribution ratio is deduced between the general contractor and the procurement service provider under the decentralized situation. Finally，a numerical example and sensitivity analysis are presented to illustrate the model，and some managerial implications are also provided.

Keywords：profit distribution；investment degree；optimal decision；capital distribution ratio

作者简介：

收稿日期：2015-10-21．

中图分类号：F284

文献标识码：A

文章编号：1674-8859（2016）01-120-05

DOI:10.13991/j.cnki.jem.2016.01.022