小生境粒子群支持向量机的网络故障诊断*

张亚梅，张正本

（河南机电高等专科学校，河南　新乡　453003）



小生境粒子群支持向量机的网络故障诊断*

张亚梅，张正本

（河南机电高等专科学校，河南新乡453003）

摘要：针对支持向量机（SVM）在网络故障诊断中应用存在的参数设置和诊断模型复杂的问题，提出一种基于小生境粒子群优化的SVM解决方案。算法在进行参数寻优的同时考虑支持向量个数，实现对诊断模型复杂度的优化，并采用小生境粒子群算法进行求解，提高算法跳出局部最优的能力。在DARPA数据集上的实验表明本文提出的方法能够有效提高诊断模型的泛化性和诊断速度。

关键词：网络故障诊断，支持向量机，小生境粒子群，支持向量数目

0　引言

网络故障诊断［1］实质上是一个模式识别问题，以核技术和结构风险最小化原则为核心的机器学习方法-支持向量机（Support Vector Machine，SVM），在解决小样本、非线性及高维问题中的优势，已被初步应用于网络故障诊断［2-4］。然而，网络开放互联的组织形式使得独立的网元具备了相关性，同一个网络故障事件可能引起多个网络监控设备的告警；此外网络作为一个分层管理系统，故障事件的影响从底层的接口、网络协议等到高层更加抽象的应用服务，由于高层网络实体对低层网络实体的依赖性，低层次的事件必定引起高层次的告警。这些特点使得对于同一事件，往往会引起数目巨大的告警信息，以百兆网络为例，仅IDS系统一小时就可产生上百万条的告警记录，给网络故障诊断系统带来非常大的压力。这就要求网络故障诊断模型尽可能地简单，而采用SVM方法建立的诊断模型复杂程度是由支持向量的个数决定的，支持向量个数越少，模型越简单。但是，当训练样本集规模较大时，获得的支持向量集往往比较大，模型比较复杂。在进行SVM训练时，当前的研究一般只关注诊断的精度，忽视了模型的复杂程度。为了解决这一问题，在建立诊断模型的时候既注重诊断模型精度的同时考虑模型的复杂程度。通过智能搜索的方法找出最佳训练参数，以达到在保证诊断精度的情况下降低模型的复杂度。粒子群算法相较其他智能搜索算法具有实现简单、收敛速度快等优点，因此，被大量应用于SVM的参数选择上，但是它也容易陷入局部最优［5-6］。Brits等人将小生境这一概念引入到粒子群算法中，提出了小生境粒子群算法（niche particle swarm optimization，NPSO）［7］，有效地解决了传统粒子群算法易陷入局部最优的问题。

基于以上分析，本文提出一种基于小生境粒子群SVM的网络故障诊断方法。在NPSO对SVM训练参数进行寻优同时考虑所建立模型的复杂度，实现对所构建模型的简化，提高诊断模型泛化性。

1　基本理论

1.1 SVM原理及分析

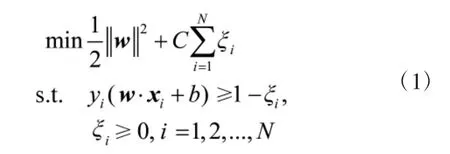
则，式（1）的对偶问题如式（2）所示

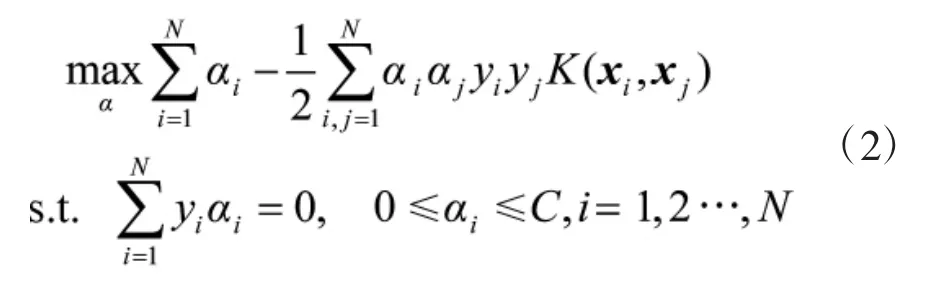
式中K（xi，xj）=φ（xi），φ（xj）为核函数，求解该二次规划问题得到问题的最优判决函数为：

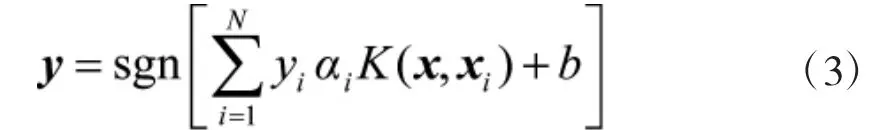
SVM是一个二分类问题，它的分类模型经验风险和实际风险之间满足下面的关系：

R≤Remp+Φ（l/h）（4）

Φ为置信范围，l为样本个数，h为分类模型的VC维。从式（4）可以看出置信范围越小，经验风险最小化的最优解就会接近实际的最优解。而置信范围Φ是（l/h）的单调递减函数，对于一个特定的问题，其样本数l是固定的，此时学习机器的VC维越高（复杂度越高），则置信范围越大，导致真实风险与经验风险之间可能的差就越大。这就是为什么在一般情况下选用过于复杂的分类器或神经网络往往得不到好的效果的原因。因此，机器学习过程中不但要使经验风险尽可能小，还要使VC维尽可能小，以缩小置信范围，才能使实际风险最小，从而对未来的样本有较好的推广性，而SVM中VC维与支持向量的个数有关，支持向量个数越多VC维越高。

下面，进一步分析SVM参数与分类精度的关系。本文中使用径向基（RBF）核函数，SVM的分类精度与惩罚因子C和核参数g有关。图1给出了Wine数据集的C、g与SVM分类精度的对应关系：

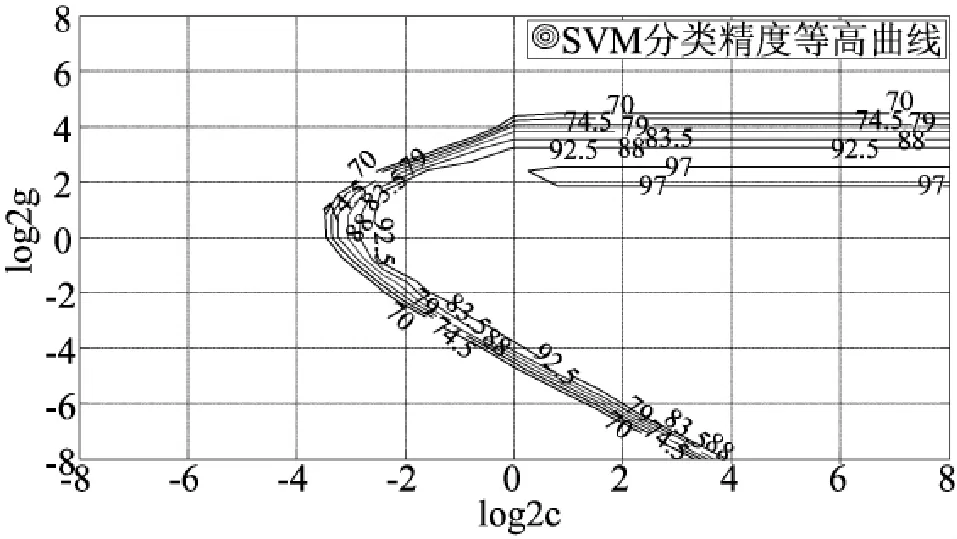
图1 Wine数据集SVM参数与精度关系曲线

从图1中可以看出SVM的寻优曲线是比较长的，以分类精度为92.5%的等高线为例，可以发现g的范围大概从2-8~ 23，而C的范围大概是2-3~ 28，也就是在这个等高线上的所有点分类精度均为92.5%。但是不同参数值对应的分类模型是不同的，它们的支持向量个数也是不同的，同样分类精度为92.5%，有的模型支持向量个数非常多，VC维比较高，模型就很复杂，而有的支持向量就比较少，对应的模型也就相较简单，泛化性更好一些。我们的目标是在相同的分类精度条件下找出支持向量个数最少的模型。

1.2小生境粒子群算法

粒子群算法是Kennedy和Eberhart模仿鸟类群体行为的智能优化算法，可解决连续函数的优化问题［5］。在算法中，群体中的每个粒子都是一个潜在的解，通过学习历史中自身的最优位置pb和群体最优位置pg来更新位置和速度，并根据粒子的位置计算适应度函数来判断解的优劣，不断迭代找到最优解。

若粒子群的搜索空间为D维，粒子的位置和速度分别为Pi=（pi1，pi2，…，piM）和Vi=（vi1，vi2，…，viM），则其迭代公式为：

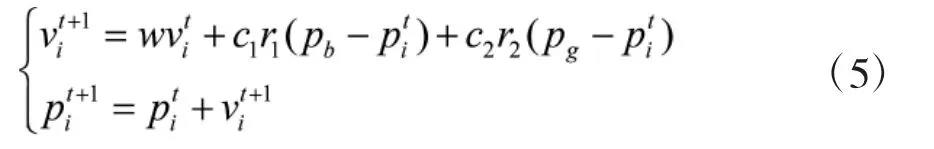
其中，w为惯性常数，t为迭代次数，c1和c2为学习因子，r1和r2为［0，1］之间的随机数。相较遗传算法，PSO的搜索过程具有方向性，因此，收敛速度更快，但同时也容易陷入局部最优解。小生境是来自生物学的一个概念，是指特定环境下的一种生态环境，若干物种在一定区域内形成小生境，小生境之间的基因由于自然隔离缺乏交流使得物种之间的差异得以保留。将这种概念运用到优化上来说就是将每一代的个体划分为若干个类，依据某种规则从每个类中选择出适应度较大的个体作为类的代表，在类内和类间进行杂交、变异产生新一代个体。这样就有助于算法跳出局部最优，而从SVM的分类介绍可以看出它参数选择问题的局部最优解非常多，因此，这里才有NPSO方法进行寻优，它与PSO最大的不同是在搜索过程中选出若干个适应值变化较小的粒子，以这些粒子为中心，据此粒子最近的粒子之间距离为半径构造圆形小生境，定义小生境半径为：

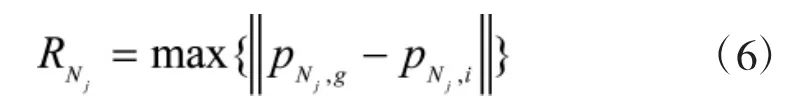
其中，pNj，g，pNj，i分别为子粒子群中最优粒子和任意非优粒子，通过小生境的构造来保证粒子的差异，也就更容易达到全局最优。

2　 NPSO-SVM算法

2.1算法描述

NPSO-SVM算法通过NPSO对SVM的参数进行寻优，与其他方法不同的是本文的目标函数中考虑了得到分类模型的复杂度。前面提到，分类模型的复杂度与支持向量的个数有关，这里设计目标函数为：

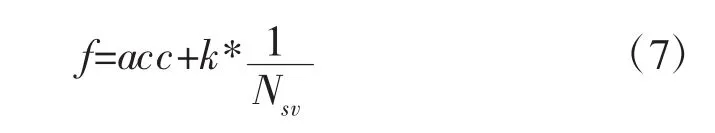
其中，acc为分类模型的精度，这里采用交叉验证的方式获得，Nsv为支持向量个数，k为常数，这里取0.5。

NPSO-SVM算法的具体步骤如下：

STEP1：设置算法参数，初始化主粒子群；

STEP2：使用PSO对主粒子群进行搜索，选出若干个适应值变化较小的粒子，以这些粒子为中心，据依据式（6）构造圆形小生境；

STEP3：对每个子粒子群进行如下操作：

①使用PSO更新粒子：

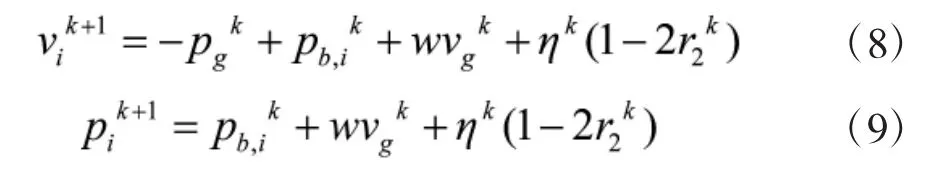
其中η为搜索范围最大值；

②计算每个子粒子群的适应值；

③更新子粒子群小生境半径；

④若两个子群Nj和Nk范围相交，即，则合并两个子群；

⑤若粒子pi进入子群Nj范围，即，则该粒子将被此小生境粒子群吸收；

STEP4：重复步骤STEP3直到达到最大迭代次数或结果满足要求，算法结束。

2.2算法验证

为了验证所提算法的有效性，用人工数据集进行分类实验，人工数据集包括正负类样本各100个，可以完全分开。这里分别采用不考虑分类模型复杂程度的PSO-SVM［6］以及本文的方法进行实验，观察分类面和支持向量个数。实验环境为Pentium（R）Dual-Core2.7 G CPU，4 G内存，Windows XP系统，Matlab 8.2。实验结果如图2所示。

图2人工数据集实验结果

从实验结果可以看到无论是否考虑模型复杂度的PSO-SVM［］还是本文的NPSO-SVM，训练得到的分类面均可以将两类样本完全分开，这是由于SVM作为一种先进的机器学习方法，本身具有较强的泛化性。再观察支持向量个数，可以发现PSO-SVM的支持向量个数为14个，而本文方法仅为两个，这主要是因为传统的PSO-SVM方法仅考虑分类精度，这样算法马上收敛于一个分类精度达到100%的点，没有进一步地考虑模型的复杂度和分类模型的泛化性，而本文方法同时考虑了模型的复杂度，对得到的分类模型进一步优化。从最终分类面也可以明显看出本文方法获得的最优分类面泛化性优于传统的方法。

以下分析算法的收敛性，这里分别采用粒子群算法（PSO）和本文的小生境粒子群算法（NPSO）对参数进行搜索寻优，以Benchmarks中的Splice数据集为例，正类样本个数600个，负类样本400个，优化目标函数均为式（7），仿真结果如图3所示。

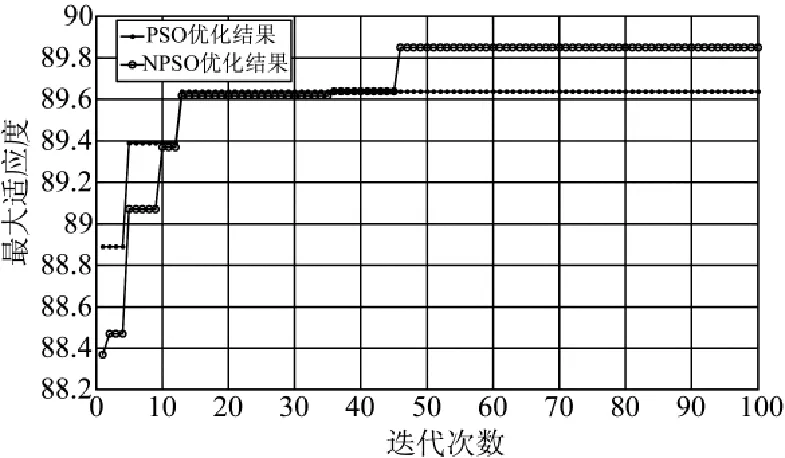
图3参数寻优结果比较

从图3可以看出，PSO-SVM快速收敛于0.8964，而NPSO-SVM收敛速度虽然慢于PSO-SVM，但是它能达到更好的收敛结果，达到了0.898 6，这说明PSO-SVM最终收敛于局部最优解，而NPSO-SVM由于加入了小生境思想，使得优化过程更容易跳出局部最优。从收敛过程也可以看出，虽然NPSO-SVM在36代时也达到了局部最优0.896 4，但是它很快于45代时跳出这一局部最优解，直观地体现了本文方法的优势。

为了充分说明本文提出方法的有效性，对Benchmarks的其他样本集分别做分类实验。分别比较不考虑模型复杂度的PSO-SVM和本文方法的分类精度和支持向量个数，获得的实验结果如表1所示。

从实验结果可以看出本文方法在分类精度上没有任何下降，在Diabetis、Image和Thyoid数据集上还有一些提高，从这里可以看出NPSO算法相较PSO算法的寻优能力更强，更容易达到最优解。除此之外，本文方法在支持向量（SV）个数上均有明显减少，降低了分类模型的复杂性，提高了模型的泛化性。

表1 Benchmarks实验结果

3　基于NPSO-SVM的网络故障诊断

由于目前网络中各种攻击事件和病毒越来越多，导致网络中产生大量的“软故障”。本文选择了DARPA99入侵数据集，以攻击下的网络状态模拟网络故障。该数据集包含4类网络攻击，分别是DOS、Probe、R2L和U2R，用一套标准格式的数据来记录各种网络状态下的特征，每条记录均有41个特征值。为了确保数据的普适性，从原始数据集中以等间隔采集法选取训练集样本和测试样本，具体的样本选择情况如表2所示。

表2实验样本集

分别采用PSO-SVM，NPSO-SVM进行特征选择，粒子群算法种群规模均为20，最大迭代次数100，比较两种算法的诊断精度和支持向量个数以及诊断时间，实验结果如表3所示。

从实验结果可以看出相较传统的仅以诊断精度为优化目标的PSO-SVM算法，本文提出的NPSO-SVM在诊断精度和诊断时间上均有提高，说明本文提出的诊断算法能够在保证诊断精度的同时简化得到的诊断模型，有效解决参数寻优和模型复杂的问题。

表3故障诊断结果

4　结论

SVM作为一种优秀的分类方法被引入到网络故障诊断问题中，但是SVM的参数寻优以及诊断模

型复杂问题影响它的应用效果。本文采用NPSO算法对SVM参数进行寻优，解决寻优过程中容易陷入局部最优的问题，同时用支持向量个数表示模型的复杂度，加入寻优过程中，提高获得的诊断模型的泛化性。在DARPA数据集上的网络故障诊断实验表明本文提出的方法能够快速达到在保证诊断精度的同时降低模型的复杂度，提高诊断速度，为SVM在网络故障诊断提供一种新的思路。

参考文献：

［1］GR尴NB覸K J，SCHWEFEL H P，CECCARELLI A，et al. Improving robustness of network fault diagnosis to uncertainty in observations［C］// IEEE International Symposium on Network Computing and Applications，2010.

［2］温祥西，孟相如，马志强.基于双重支持向量机的网络故障诊断［J］.控制与决策.2013，28（4）：506-510.

［3］朱长成.支持向量机在网络故障诊断中的应用［J］.计算机仿真，2011，28（10）：03-107.

［4］GUO J W，WU X P，YE Q. Network fault diagnosis based on rough set-support vector machine［C］// ICCASM 2010，2010.

［5］向昌盛，张林峰. PSO-SVM在网络入侵检测中的应用［J］.计算机工程与设计，2013，31（4）：1222-1225.

［6］左磊，侯立刚，张旺，等.基于粒子群-支持向量机的模拟电路故障诊断［J］.系统工程与电子技术，2010，32（7）：1553-1556.

［7］BRITS R，ENGELBRCHTA P，BERGH Fn. A niching particle swarm optimizer［C］// Proceedings Conf. on Simulated Evolution and Learning，Singapore，2002.

［8］VAPNIK V. Statistical learning theory［M］. New York：Wiley，1998.

Network Fault Diagnosis Based on Niche Particle Swarm Optimization SVM

ZHANG Ya-mei，ZHANG Zheng-ben
（Henan Mechanical and Electrical Engineering College，Xinxiang 453003，China）

Abstract：The parameters setting and diagnosis model complexity caused by dataset’s huge size affect the SVM’s application in network fault diagnosis. A new method based on niche particle swarm optimization SVM is proposed to solve these problems. The algorithm optimizes SVM training parameters，and the support vectors number is proposed to simplify the diagnosis model complexity as well. The niche particle swarm optimization method was introduced to this optimization problem while it’s excellent ability of escape locally optimal solution. The experiments on DARPA dataset shows that the method can improve the diagnosis model’s generalization and can get faster diagnosis speed.

Key words：network fault diagnosis，SVM，niche particle swarm optimization，support vector number

作者简介：张亚梅（1963-），女，河北唐山人，副教授。研究方向：计算机网络、软件应用。

*基金项目：河南省教育厅自然科学研究计划基金资助项目（2011B520013）

收稿日期：2014-12-22

文章编号：1002-0640（2016）02-0158-04

中图分类号：TP393

文献标识码：A

修回日期：2015-02-23