武器装备体系能力矩阵评估方法*

曹　强，荆　涛，周少平

（海军装备研究院，北京　100161）



武器装备体系能力矩阵评估方法*

曹强，荆涛，周少平

（海军装备研究院，北京100161）

摘要：针对武器装备体系能力难以客观、定量评估的问题，引入复杂网络理论，提出了基于矩阵运算的武器装备体系能力评估方法。分析了武器装备体系能力的概念，建立了武器装备体系的复杂层次网络模型，描述了装备网络的组成、运行过程，定义了装备网络的矩阵描述方法和矩阵运算规则，提出了装备网络作战能力描述参数，给出了装备网络能力的矩阵计算方法，进行了影响因素分析，最后通过实例验证了方法可行性、有效性和灵活性。

关键词：武器装备体系，复杂网络，能力评估，矩阵，敏感性

0　引言

传统的武器装备体系能力评估方法通常采用先自顶向下对体系进行分解，再自底向上逐层聚合各种战技术指标的方式，这种评价方式体现了装备性能对体系能力的影响，但忽略了装备间的关联依赖关系以及运行方式对体系整体能力的影响。

在电子信息技术的推动下，武器装备体系日益网络化、一体化。近年来复杂网络理论的繁荣与发展，也为武器装备体系能力的评估提供了有益的借鉴。

1　武器装备体系能力

能力（capability）是做事的本领，是“能胜任某项任务的主观条件”。作战能力，《军语》释义是［1］，“亦称战斗力。武装力量遂行作战任务的能力。由人员和武器装备的数量，编制体制的科学化程度，组织指挥和管理的水平，各种保障勤务的能力等因素综合决定”。美军认为［2］“能力是武装力量在规定的条件下和标准下，使用作战要素执行一组任务并达成作战目标效果的本领”。目前国内对能力的认识与美军接近，即认为能力是一种达到所期望效果的本领，即在特定标准和条件下通过使用各种方法、手段和信息完成一组任务后得到期望效果的本领［3］。

能力通过作战加以反映，称为作战能力。武器装备体系能力、作战部队能力、武器系统能力等都是作战能力在某个方面的具体形式。

武器装备体系的能力可用最小、最大及平均能力3个值来描述。最大能力是设计者赋予武器装备体系的理想能力，表现为系统的功能和性能指标。武器装备体系的能力通过任务的执行过程释放，实际能力常比最大能力小，制约能力发挥的环节和因素越多，实际能力与理想能力的差距越大。

作为武器装备体系的设计者、论证者，应更注重通过体系能力的评估，探寻并消除影响体系最大能力发挥的环节和因素。

2　武器装备体系网络建模

2.1节点与边

一个网络图G定义为集合（V，E），记为G=（V，E）［4］。其中V是节点集合，E是边的集合，而一条边是两个节点的有序或者无序对，即V×V或者VΔV。如果任意点对（i，j）与（j，i）对应同一条边，则该网络为无向网络，否则为有向网络。

武器装备体系可以抽象成复杂网络，即由许多的具有自主特性的装备节点以及表示装备间复杂关联依赖关系的边组成，简称装备网络。

装备网络中的节点按照功能可分为3类：

①传感器：主要由侦察、探测、监视类装备组成，提供目标信息和战场态势信息。

②决策中心：主要由一体化的C4I系统组成，又可以分为通信节点、决策节点和指控节点等。

③战斗单元：主要由软、硬杀伤武器组成，接收决策中心的指令实施作战行动，毁伤或使目标失去作战能力。

装备网络中的边，按照信息能否双向流动地分为单向边与双向边，按照边是否存在实际的通信链路连接分为虚拟边与实连边。目标到传感器是单向的、虚拟的边，传感器与决策中心、决策中心与战斗单元都是双向、实际连接的，战斗单元与目标之间也是单向、虚拟的边。决策中心内部通信节点、决策节点、指控节点之间的边都是基于通信链路的双向实连边。

2.2层次与运行过程

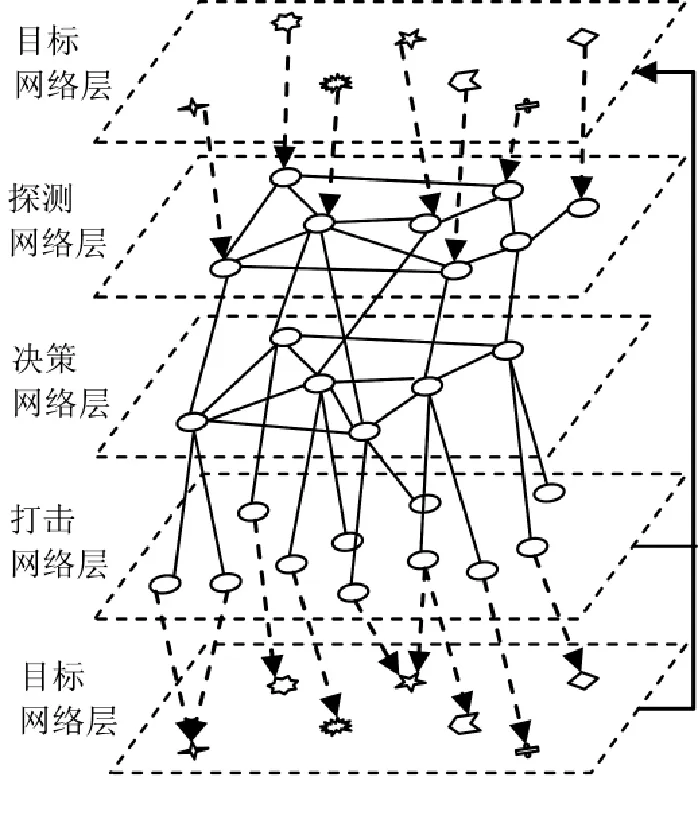
图1武器装备体系的层次网络模型

网络层次化有利于分析网络的运行过程和节点间复杂的关联关系。依据网络节点和边的不同，将装备网络划分为探测网络层、决策网络层、打击网络层、目标网络层4层，如图1所示。目标网络层的构成比较复杂，既包括敌方武器装备网络和自身发射出的网络化、智能化的武器，又包括传感器探测到的自身网络中的其他节点和边。

装备网络的作战运行过程：决策中心依据传感器获取的目标信息和战场态势，结合作战任务作出行动决策，战斗单元实施作战行动后，传感器获得打击效果及新的战场态势，重复上述过程。这一过程与现代作战理论中的观察（Observe）、判断（Orient）、决策（Decide）、行动（Act）——OODA环是一致的。

2.3矩阵描述与运算

2.3.1单层（single-layer）网络矩阵描述

装备网络中的各层网络由同质的节点组成，除非特别说明了信息的流向，认为节点间是双向的。按照复杂网络理论，这样的网络可以用邻接矩阵A描述。

单层网络是一个n阶无向图，关联依赖矩阵是一个n×n的对称方阵。矩阵元的定义是：

式中，wij＞0，为节点i与节点j邻接边的权，wii=1节点与自身的关联为1。

目标网络层和打击网络层中节点间如果没有边连接，用单位阵I表示；其余网络层中边的权值用信息传输成功概率、传输时延等装备理论设计指标或实际使用中的统计均值描述。

2.3.2层间（inter-layer）网络矩阵描述

不同层网络之间的关联依赖用转移矩阵T表示。m阶网络层与n阶网络层之间的关联依赖是一个m×n的转移矩阵。转移矩阵元的定义是：

式中，ωij为节点i与节点j邻接边的权，值的确定方式与单层网络矩阵阵元类似。

对于单向边规定：起始节点指向末端节点时取正值，反之取负值。

2.3.3运算规则

装备网络矩阵除了满足一般矩阵的运算规则外，还有以下特殊运算规则。

①拼接与分块

用水平和垂直的虚线将Am×n矩阵中的元素阵列分成小块（子阵）的操作，称为矩阵的分块。例如：

拼接是上述操作的逆运算，即将子矩阵（网络）合成行列数更多的矩阵（大网络）的过程。

装备网络中的分层实际上就是对整个网络的分块，将子阵当作普通矩阵的元素进行运算。

②链路及数量

图论中，链和路是不同的概念，无向图中的链即为有向图中的路。装备网络是有向图与无向图并存的复杂网络，将链和路作为一个概念，定义为从任意一层网络节点到其他层节点所经过的边和节点的集合。为提高网络效率，设同一层内的链路传播不超过2个节点。

将各单层网络矩阵和层间网络矩阵中的边权都置为1，并按照装备网络运行的过程作矩阵乘法运算，称为链路数量求取运算。有图2所示的两层网络，可用单层网络矩阵A1、A3和层间网络矩阵A2描述。

图2链路长度计算示例网络

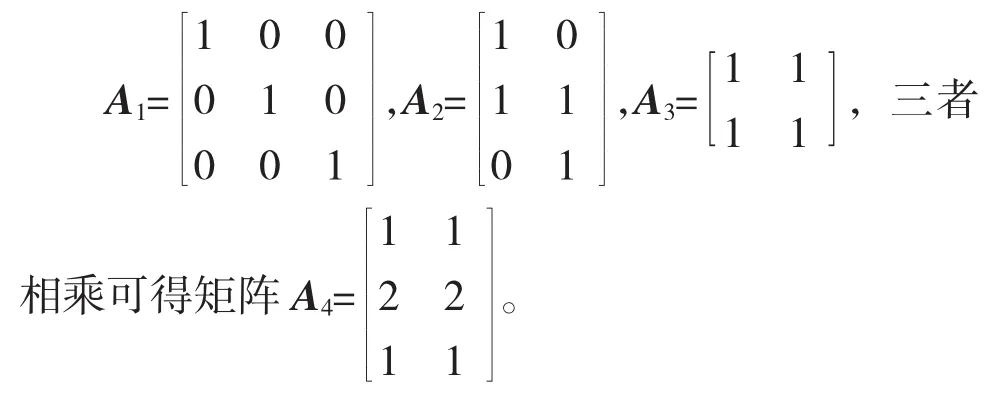
A4中矩阵元表示起点与终点之间的链路数量，不难看出，上层节点2至下层节点4和5的链路数量为2。

示例中网络的平均链路数为1.333 3条。

③融合与分配

融合是指多传感器对目标数据的融合，分配指的是不同武器对目标的火力分配与打击。两者分别用m×1的联合目标探测概率列向量JD和1×n的联合目标毁伤概率行向量JK表示，向量中的元素定义如式（4）、式（5）所示。

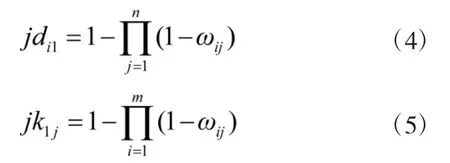
多传感器融合与有效火力分配可以大大增加武器装备体系获取目标、打击目标的概率，有效发挥体系的作战能力。如两个传感器对某一目标的探测概率分别是0.8和0.7，则融合后体系对目标的联合探测概率为0.94。

2.4参数描述

2.4.1网络性能参数

装备网络是典型的复杂网络。对复杂网络性能的分析通常采用网络统计特性描述，其定义和计算方法参阅相关文献，这里仅给出它们在装备网络中的物理含义。

①节点与链路数量

节点的数量反映了装备的规模，边的数量反映装备互联互通的复杂程度。平均链路数量则反映了网络运行的平均开销和性能；介数是网络节点重要性的度量。

②流量与度分布

流量是网络边负载的描述，装备网络中反映边的重要性。度及其分布描述网络的连接模式，能够一定程度反映网络的适应性和抗毁性。

③距离与效率

距离反映实现两个节点连通所需花费的大小，效率表示网络平均交通的难易程度。特征路径长度（CPL）是网络中节点到所有其他节点的平均距离的中值（顺序排列的数值的中间值）。小的特征路径长度意味着通过网络进行信息扩散是不必经过很多节点。有人将其定义为平均路径长度，即为网络中任意两个节点间的距离的平均值。最短路径则是装备网络中效率最高的路径，是网络最佳能力的测度。

④鲁棒性与脆弱性

鲁棒性用来衡量网络避免灾难性失败的能力；脆弱性用来描述网络对节点的依赖程度，网络的脆弱性用最脆弱节点的脆弱性表示。

2.4.2作战能力参数

除传统的网络参数外，针对武器装备体系遂行作战任务的过程、特点提出以下装备网络能力描述参数：

①目标探测能力

装备网络的探测能力实际上就是传感器网络的探测能力，可用网络对目标的联合探测概率JDm×1和探测距离描述。

需注意，目标的类型、距离与发现概率之间的制约关系，目标的类型与传感器不匹配，发现概率为0，目标的距离超出探测器最大发现距离，发现概率为0。

②网络决策能力

装备网络的决策能力是目标传输（包括网内传输、网间传输）能力、目标处理能力和目标分发能力三者的综合。

目标传输能力可用信息传输的精准度（误码率和成功率）和信息通道（网络边）的容量（capacity）衡量。

目标处理能力用处理目标信息的数量和所需的时间描述。

目标分发能力是指控系统通过目标打击指令（方案）控制战斗单元的能力，包括指控的精度（成功概率）和数量（火力通道数）。

整个网络的决策能力可以用目标信息从传感器成功传输至战斗单元的概率和传输过程的时延描述。

③目标打击能力

装备网络的打击能力实际上就是战斗单元对各个目标的软硬杀伤能力，常用战斗单元对目标的联合毁伤概率JK1×n和打击距离描述。

目标的类型、距离与毁伤概率之间存在制约关系，目标的类型与战斗单元不匹配，毁伤概率为0，目标的距离超出战斗单元最大打击距离，毁伤概率也为0。

④综合作战能力

装备网络的综合作战能力是武器装备体系完成作战任务，达到期望效果的本领。在作战过程中，无论是“保存自己”还是“消灭敌人”，都需要在特定的标准和条件下，通过打击/抗击各种敌方目标来实现。因此，可以用装备网络有效运行的条件下，对各目标的毁伤能力表示综合作战能力。

装备网络的运行状态和反应能力分别用平均链路数量和特征路径的长度描述，毁伤能力通常用平均毁伤概率表示。平均链路数量越大说明可用信息通道越多，网络的抗毁性越好，也会造成平均传输延时的增加，网络运行效率的下降。

3　装备网络能力评估

3.1模型假设

设某装备网络中有传感节点M个，通信节点N个，决策节点O个，指控节点P个，打击节点Q个；各个节点之间的连接关系已知，并且可以更改。

设有R类目标，每类目标有S个；其中，第m个传感器以概率pmr发现r类目标的最大距离为ddmr；第q个武器在最大距离为dkqt处毁伤t目标的概率为kqt。

设传感器网络对各目标的发现概率用矩阵DM×R表示，武器单元对各目标的毁伤概率用矩阵KQ×R表示；传感节点、通信节点、决策节点、指控节点、打击节点之间的关联依赖关系分别用层间网络矩阵TM×N、TM×O、TO×P以及TP×Q表示；传感节点、通信节点、决策节点、指控节点、打击节点内部的关联依赖关系分别用单层网络矩阵AM×M、AN×N、AO×O、AP×P以及AQ×Q表示。

3.2能力评估计算

3.2.1平均（综合）作战能力

用平均链路数量表示的上述装备网络的综合作战能力CLsos由式（6）决定：

其中，TM→Q为传感节点与战斗单元之间的可用链路数矩阵，由下式计算。

TM→Q=AM×M·TM×N·AN×N·TN×O·AO×O·TO×P·AP×P·TP×Q·AQ×Q（7）

如果式（7）中各矩阵中元素为信息传输的概率，则用平均毁伤概率表示的上述装备网络的综合作战能力CPsos由式（8）决定：

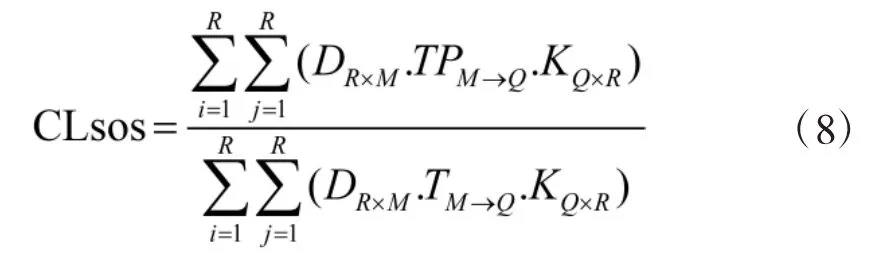
其中，TPM→Q为传感节点与战斗单元之间的可用链路的概率累加值矩阵，计算方法同式（7），仅将各子矩阵中的元素用边权替代即可。

若装备网络具备联合探测、联合火力打击能力，则式（8）变为：

式（9）实际上是将装备网络看成一个整体，将其对目标的联合探测概率、联合毁伤概率以及自身对目标信息传输的平均损失概率相乘得到装备网络的平均毁伤概率。

采用矩阵方法计算装备网络的综合作战能力，对网络结构的变化具有较强的适应性。增加、删除节点，只需要增加、删除对应矩阵中行和列的元素，增加、删除网络层，只需要增加、删除相应的子矩阵即可。进行上述操作时，需要注意矩阵之间行列数量运算的匹配性。

3.2.2最大作战能力

装备网络的最大作战能力是最大目标容量、最小网络延迟时间和最大毁伤概率的函数。

最大目标容量由传感器和指控系统战技术指标决定；对于己方已有系统最大目标处理数量一般可知，对于设计中的系统可以假设一个水平值。

最小网络延迟是装备网络从发现目标到实施打击的各个环节中耗时最少的环节，可通过求取边权为时间的装备网络最短路径获得。

最大毁伤概率是装备网络从发现目标到毁伤目标的各个环节概率积的最大值，装备网络的最大毁伤概率为各目标最大毁伤概率的平均，计算式如下：

CPsosmax=maxDR×M·maxTPM→Q·maxKQ×R（10）

式中max运算表示取矩阵中元素的最大值。当存在联合探测和联合火力打击时需要用JDR×1和JK1×R代替式（10）中的DR×M和KQ×R进行计算。

3.2.3最小作战能力

装备网络的最小作战能力仅是最大延迟时间和最低毁伤概率的连续函数，目标容量为0，装备体系的作战能力为0。

最大延迟时间是装备网络从发现目标到实施打击的各个环节中耗时最多的环节，一般通过求取边权为时间的装备网络最长路径获得。

最小毁伤概率是装备网络从发现目标到毁伤目标的各个环节概率积的最小值，装备网络的最小毁伤概率为各目标最小毁伤概率的平均，计算式如下：

CPsosmin=maxDR×M·maxTPM→Q·maxKQ×R（11）

式中min运算表示取矩阵中元素的最小值。存在联合探测和联合火力打击时，用JDR×1和JK1×R代替式（11）中的DR×M和KQ×R进行计算。

3.3影响因素分析

影响装备网络能力发挥的主要因素有节点状态、连接方式和作战环节。

装备网络的敏感影响因素分析采用理想4层（含目标层）最大连通网络，每层网络拥有N个节点，每个节点都与层内和层间的节点有一条边相连，边的权（信息传输概率）为1。一般情况下目标层中各节点之间仅存在较少的连接，为计算简便，假设目标层中各节点独立。由式（6）～式（9）可计算得到该装备网络用平均链路数量表示的作战能力为N4，毁伤目标的概率为1。若网络的层次扩展至F层（含目标层），平均链路数量增至NF。

在上述网络的基础上，N、F不变，均匀删除一定比例（如x）的单层连接，则用平均链路数量表示的作战能力降为（1-x）-（F - 1）.NF，表现出网络层越多能力呈指数下降越明显的特点。

在F层最大连通网络的基础上，其余不变，仅网间连接的边权重均变为ω，则装备网络的平均毁伤概率降为ωF，当F为4，ω等于0.99时，整个网络的毁伤概率值降为0.97，同样呈现出指数下降的特点。

若既删除x比例的单层连接，又将网间连接的边权重均变为ω，则整个网络的平均毁伤概率为（1-x）-（F - 1）.ωF.NF，作战能力出现了指数叠加下降的效应。

4　实例

设某武器装备体系由3个传感节点，2个通信节点，1个指控节点，2个打击节点组成，其各节点之间的连接关系以及各边的权重（概率）如下页图3所示。

示例中，传感器对目标的探测概率、火力单元对目标的毁伤概率分别由矩阵D3×3和K2×3中的值决定。

图3实例网络结构

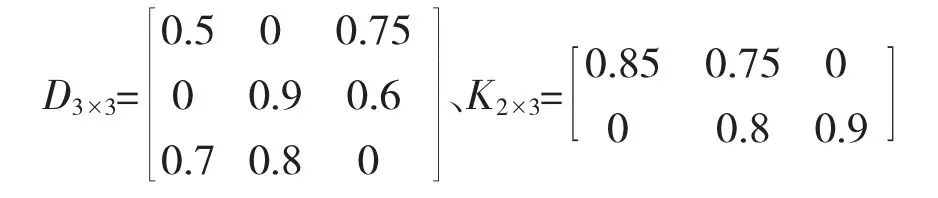
融合后体系对目标的联合探测概率JD3×1为［0.875 0.96 0.94］T，联合毁伤概率JK1×3为［0.85 0.95 0.9］；若探测、通信、指控、打击网络内部与之间的通信绝对可靠，由式（6）～式（8）可求得，装备体系的平均链路数量为4、平均毁伤概率为0.833 9，最大（对目标2）、最小（对目标1）毁伤概率分别为0.912、0.743 8。

若按图3中的标注的各边权值计算，装备体系的平均链路数量不变，平均毁伤概率降为0.749 3，最大、最小毁伤概率分别降为0.823 7、0.664 8。

对上述网络进行重新设计和能力计算：

实验1：删除通信层，探测网络直接与指控节点相连，边权保留原探测层至通信层的值。则装备体系的平均链路数量不变，平均毁伤概率提升为0.760 5，最大、最小毁伤概率分别提升为0.840 5、0.681 9。

实验2：增加含3节点互联的决策层，决策层插入通信层与指控层之间，决策层节点与通信层节点两两相连，且边权为1，决策层与指控层也是两两相连，边权为原通信层与指控层相连的值0.99。这时，装备体系的平均链路数量增至12，平均毁伤概率不变仍为0.749 3，最大、最小毁伤概率仍为0.823 7、0.664 8。

实验3：改变连接关系，让传感器之间不互联，体系对目标的探测概率为各类传感器发现目标的最大概率。按图3中的标注的各边权值计算，装备体系的平均链路数量为4/3，平均毁伤概率下降为0.574 7，最大、最小毁伤概率分别降为0.780 3、0.375 9。

实验4：面对同一目标群，将探测网络至打击网络的节点按照每一层从左到右，各层从上到下的顺序给每个节点编1号~8号，然后让每个节点依次失效，每次仅失效一个节点，计算上述过程中装备网络能力的变化。结果如图4、图5所示，可知节点6（图3中着红色标识）对于支撑该网络运行最为重要，节点4次之。

图4节点失效导致装备网络运行能力的变化

图5节点失效导致装备网络作战能力的变化

上述实验说明：武器装备的互联、互通能够大大提高武器装备体系的能力；作战环节和网络层级的减少也会提高武器装备体系的运行效率和作战能力；增加可靠的通信节点和链路不会降低作战能力，但会提高体系的连通能力；网络的连接形式对装备网络能力的影响很大，在设计武器装备体系时需要重点研究；基于矩阵的装备网络能力计算方法能够有效反映网络结构变化所引起的体系能力变化，可用于武器装备体系脆弱性的分析。

5　结论

采用矩阵对装备网络进行描述和计算，具有便于计算机实现且形式更为规范和简洁的特点。文中提出的武器装备体系能力的矩阵评估方法，能够计算有权装备网络中任意两个节点之间的平均链路数，信息获取、传递效果，火力运用效果等作战能

力，能够计算任意节点或边的变化导致的网络结构变化后作战能力的变化，为分析装备网络的脆弱性、设计武器装备体系、评估体系的效能等后续应用提供了有力的方法支撑和借鉴。对于武器装备体系的设计者、论证者来说，在考虑网络能力提升的同时，还需要进一步权衡能力提升带来的系统运行效率的可能下降和构建维护费用的提升等问题。

参考文献：

［1］全军军事学术管理委员会.中国人民解放军军语［M］.北京：军事科学出版社，2011.

［2］DoD. DoD architecture framework version 2.0［M］. Washington DC：Department of Defense，2009.

［3］胡晓峰，杨镜宇，司光亚，等.战争复杂系统仿真分析与实验［M］.北京：国防大学出版社，2008.

［4］何大韧，刘宗华，汪秉宏.复杂系统与复杂网络［M］.北京：高等教育出版社，2009.

［5］胡晓峰.战争复杂性与复杂体系仿真问题［J］.军事运筹与系统工程，2010，24（9）：27-34.

［6］HAN E P，DELAURENTIS D. A network theory-based approach for modeling a system-of-systems［C］//11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference，2006.

［7］MUHARREM M，DELAURENTIS D A. Network-level metric measuring delay propagation in networks of interdependent systems［C］// 5th International Conference on System of Systems Engineering，2010.

［8］张维明，刘忠，阳东升，等.体系工程理论与方法［M］.北京：科学出版社，2010.

［9］张春华，张小可，邓宏钟.一种基于作战环的作战体系效能评估方法［J］.电子设计工程，2012，20（21）：62-64.

［10］赵青松，鲁延京，李善飞.面向使命任务的武器装备体系能力关联分析［J］.火力与指挥控制，2011，36（3）：24-27.

Matrix Methodology Based Capability Evaluation of Weapon System of Systems

CAO Qiang，JING Tao，ZHOU Shao-ping
（Navy Academy of Armament，Beijing 100161，China）

Abstract：In order to evaluate capability of weapon system of systems more objectively and quantitively，complex networks theory is introduced，and a new matrix capability evaluation methodology is put forward. The capability definitions of weapon system of systems are analyzed，a layered complex network model of weapon system of systems is built，the components and operation process of the weapon network model are also described. Then matrix expression methods of weapon network and its special calculate rules are defined，tailor-made operation capability indexes of weapon network are brought out. The algorithm of using single-layer-matrixes and inter-layer-matrixes to compute whole weapon network’s capability is present; the influence factors of the algorithm are detailly analyzed. By the case study of a nominal operation network，the feasibility，validity and flexibility of proposed methodology are proved.

Key words：weapon system of systems，complex network，capability evaluation，matrix，sensibility

作者简介：曹强（1981-），男，江苏扬州人，博士后。研究方向：武器装备体系结构评估与优化、武器装备体系建模与仿真。

*基金项目：中国博士后科学基金（2012M521895），海军重点基金资助项目（NAA-201202-JN1-ZH009）

收稿日期：2015-01-06

文章编号：1002-0640（2016）02-0142-06

中图分类号：TP391.9，N945

文献标识码：A

修回日期：2015-03-07