基于费效分析的装备延伸保修购买决策*
2016-03-24杨志远程中华邓立杰
杨志远,程中华,邓立杰
(军械工程学院,石家庄 050003)
基于费效分析的装备延伸保修购买决策*
杨志远,程中华,邓立杰
(军械工程学院,石家庄050003)
摘要:保修机制是部队引入承制方装备维修力量的重要途径,延伸保修对装备的寿命周期费用以及承制方保修费用有很大影响。针对军方延伸保修购买决策问题,在对维修策略分析的基础上,综合考虑装备维修费用和可用度,建立了延伸保修购买决策相关模型,结合装备承制方保修成本及军方装备维修费用——效能分析,得到了在不同价格区间内延伸保修购买决策,并给出了特定条件下存在的双赢延伸保修价格区间,最后通过实例验证了模型的有效性。
关键词:延伸保修,费效分析,购买决策
0 引言
目前承制单位保障力量已经成为部队装备维修保障力量的重要组成部分,保修机制是引入承制单位保障力量的重要途径,也是常用方法。保修可以分为初始保修和延伸保修,其在装备寿命周期内的实施阶段如图1所示,初始保修期即质保期一般包含在装备的购买合同中。

图1装备寿命周期图
延伸保修对于装备的寿命周期费用及可用度具有重要影响。对于军方来说,科学地选择延伸保修可以减少维修费用,提高装备保障效益;对于承制方来说,只有当延伸保修价格大于成本时,才会提供延伸保修服务。所以延伸保修价格会直接影响双方的决策,而对于部队和装备承制方这种特殊的买卖关系,延伸保修服务的价格通常可以在合理的区间内进行协商。
国内外很多学者就延伸保修的成本费用问题进行了建模研究[1-3]。但这些研究均未考虑可用度对延伸保修决策的影响,而对于军用装备可用度又是一项十分重要的指标。鉴于此,本文在综合考虑装备维修成本和可用度的基础上,通过费用-效益分析决策是否购买延伸保修以及相应延伸保修服务价格区间。
1 延伸保修购买决策费用-效能分析过程
本文选择装备寿命周期内的平均可用度作为效能指标且只考虑装备维修费用及故障停机费用。延伸保修购买决策费用-效能分析过程如图2所示。

图2费用-效能分析过程
简单来说,就是在具体维修策略下,分别建立军方在购买和不购买延伸保修下的费效模型,结合承制方提供延伸保修服务的成本,通过对比分析装备效费比变化得出在不同价格区间下的装备延伸保修购买决策。
2 最小维修-不完全预防性维修策略
假设装备在寿命周期内的故障率是递增型,本文在装备寿命周期内所采用的最小维修-不完全预防性维修策略是指在保修期和延伸保修期内,由于装备在承制方保证下,且故障率相对较低,所以此时装备故障由生产商免费采取最小维修,维修后装备故障率不变;当装备使用超过保修期,由于此时装备工龄较长,所以故障率也随之增高,且故障损失均由军方承担,为降低故障率,预防装备在使用过程中发生故障,提高装备可用度,军方制定相应地预防性维修计划定期对装备进行不完全预防性维修,维修后装备故障率下降,介于“恢复如新”和“恢复如旧”之间。Kim(2004)[4]证明了此种维修策略存在的合理性,预防性维修可一定程度上降低后期装备的维修费用,从而降低装备的全寿命周期费用。对在预防性维修间隔期内发生的故障采用最小维修策略,这部分费用也由军方承担。
3 延伸保修购买决策模型
3.1模型假设与符号说明
对生命周期长度为L的装备进行分析,其包含长度为W的初始保修期,部队采购装备时,可以选择以CW的价格购买长度为We延伸保修服务,装备维修采取最小维修-不完全预防性维修组合策略。装备的初始故障率为r0(t),单次最小维修成本为Cr;当维修水平为m时,不完全预防性维修费用为Cm,T为不完全预防性维修间隔期。以往研究中通常不考虑维修时间影响,由于本文需要考虑装备可用度,所以相应维修时间不能忽略,令Tp为预防性维修时间,Tf为最小维修时间,假设由于维修所造成的单位时间平均损失为c。那么,部队每次进行最小维修的总费用为:Cf=C0+cTf;预防性维修总费用为:Cp=Cm+cTp。
假设装备的寿命周期内,在时间序列τ1,τ2,τ3,…,τj上进行预防性维修,假设预防性维修工作起始时间τ0=0。文中装备预防性维修工作采取不完全维修策略。本文在Kijima(1989)[5]提出的虚拟工龄法基础上,结合Sahin(1996)[6]对装备保修期过后维修策略的研究来处理不完全预防性维修策略建模问题。Kim(2004)[4]提出不完全维修后虚拟工龄的降低与维修水平m直接相关。假设维修工作的记忆性为1,即本阶段维修效果只与前一阶段状态相关,令vj表示第j次不完全预防性维修后装备的虚拟工龄,其中j≥1。那么,对于给定的维修水平m,第j次预防性维修后装备的虚拟工龄为:
vj=vj-1+λ(m)(τj-τj-1),其中v0=0(1)
其中,λ(m)表示不完全预防性维修改善因子,它是取值范围为[0,1]的关于m的减函数,因此,当维修水平m提高时,λ(m)减小,虚拟工龄减少程度就越大,即维修效果越好。令M为维修水平的最大值,此时λ(M)=0,即“修复如新”状态;当λ(0)=1时,即“修复如旧”状态。由于本文中采取不完全预防性维修策略,所以维修水平m的取值范围应为(0,M)。
在对虚拟工龄方法分析的基础上,假设在装备寿命周期内预防性维修水平均相同,即m为定值。由此,装备在t时刻的虚拟工龄v(t)可表示为:
v(t)=vj-1+t-τj-1,其中τj-1≤t<τj,j≥1(2)由于文中假设维修时间忽略不计,所以,在不完全预防性维修下,装备的故障率函数可表示为:
r[v(t)]=r(vj-1+t-τj-1),其中τj-1≤t<τj,j≥1(3)
为方便管理和实施,在实际应用中预防性维修间隔期通常是确定的,文中假设预防性维修间隔期为T。在上文分析基础上,可以得到在无延伸保修服务情况下,装备寿命周期内的预防性维修时间τj及预防性维修次数n1:
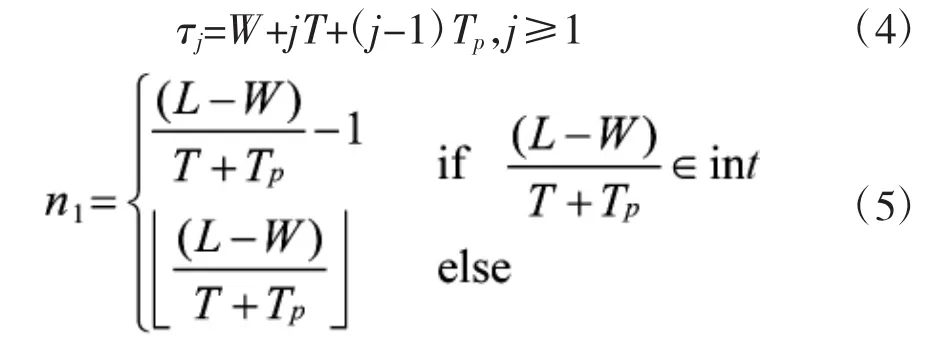
考虑到预防维修开始时刻是在保修期W结束后,在文献[4]的基础上,得到在无延伸保修服务情况下不完全预防性维修策略的装备故障率函数:

与此类似,可以得到有延伸保修服务情况下各函数的表达式。τj和n2可表示为:

不完全预防性维修策略下购买延伸保修服务装备的故障率函数:
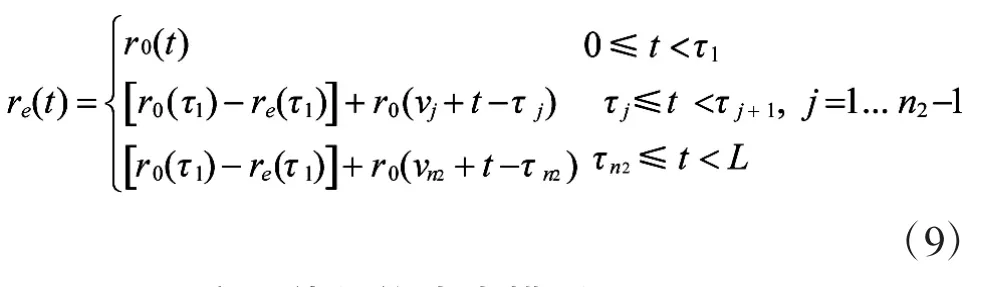
3.2承制方延伸保修成本模型
承制方提供延伸保修服务利润CP的值即为延伸保修价格以及延伸保修成本(EWC)的差值,即:
CP=Cw-EWC(10)
对生产者而言,只有CP≥0时,生产商才会提供延伸保修服务。所以,承制方所能接受的延伸保修服务的最低价格为:
Cw=EWC(11)
最小维修的特性是一个非齐次泊松过程,由此可得:

3.3军方延伸保修费用-效益模型
对军方而言,在决策是否购买延伸保修时,不仅要考虑成本问题,还需要考虑装备在寿命周期内的可用度问题。只有综合权衡寿命周期内费用和可用度,才能科学决策以提高装备保障利益。为此,我们采用寿命周期内的单位时间费效比V值作为是否购买延伸保修服务的依据,所谓寿命周期内单位时间费效比是指寿命周期内单位时间所需的维修保养费用与装备可用度的比值,它从定量角度对装备寿命周期内的维修费用和可用度进行了综合考虑。单位时间费效比函数表达式如下:

其中,A表示装备可用度,C表示与维修活动相关的费用,L表示寿命周期长度,为方便分析,这里假设装备寿命周期L为固定值。
在考虑消费者利益的情况下,消费者购买延伸保修服务后的效用应大于不购买的效用,即:
U(V1)≤U(V2)(14)
其中,U(x)为消费者的效用函数,V1为不购买延伸保修服务装备费效比,V2为购买延伸保修服务装备费效比。在本文中,当x表示费效比时,U(x)应为减函数,所以式(14)的条件可化为:V1≥V2(15)寿命周期内装备期望可用度可表示为:

式(16)中,D表示装备在寿命周期内的停机时间,它由最小维修时间和预防性维修时间构成。
在无延伸保修情况下,消费者在装备寿命周期内与维修相关的期望费用包括预防性维修费用、保修期内故障停机费用以及保修期之后的最小维修费用,可表示为:

期望停机时间包括预防性维修停机时间以及最小维修停机时间,可表示为:

由式(16)和式(18)可得装备在无延伸保修情况下的期望可用度A1为:

根据式(17)和式(19),可得装备在无延伸保修情况下对于消费者的费效比V1:

同理可得,在延伸保修服务情况下,消费者在装备寿命周期内与维修相关的期望费用为:
C2=Cnp+Cw(21)
其中,Cnp为装备寿命周期内消费者的维修费用与停机费用,其与式(17)有相同形式,可表示为:

期望停机时间为:
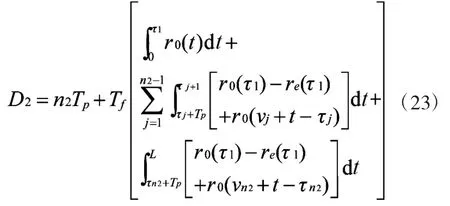
由式(16)和式(23)可得装备在延伸保修服务情况下的期望可用度A2为:

根据式(22)和式(24),可得装备在延伸保修情况下对于消费者的费效比V2:

根据式(15),可得消费者决策购买延伸保修必须具备的条件为:由此可得消费者可接受的延伸保修服务价格为:

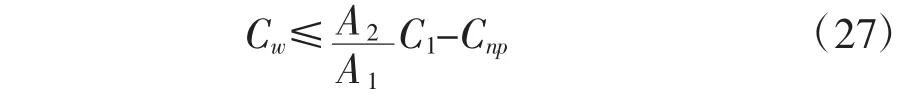
将相关函数带入(27)即可得EWPmax为:

在考虑可用度情况下,消费者购买延伸保修的综合收益CB可表示为:
CB=EWPmax-Cw(29)
在以上模型的基础上,有以下几种情况:
(1)当EWPmax≤EWC时,提供或购买延伸保修对于双方均是无效益的。
(2)当EWC<EWPmax时,有以下3种情况:
①当Cw≤EWC时,承制方不会提供延伸保修服务,此时装备需由军方自主维修;
②当EWC≤Cw≤EWPmax时,购买延伸保修既可优化装备相关维修费用和可用度,提高消费者在装备寿命周期内的效用水平,又能满足生产商的利益需求;
③当EWPmax≤Cw时,延伸保修不会提升装备维修保障效益,此时不购买延伸保修,装备由军方自主维修。
综上所述,只有当Cw∈[EWC,EWPmax]时,双方才能达成购买延伸保修服务协定,且对双方都有利。
4 示例分析
假设某装备的故障服从威布尔分布,故障率函数形式如下:

其中,β为形状参数,η为尺度参数。
对于表明不完全预防性维修效果的改善因子λ(m),本文采用kim在文献[4]中提出的形式:
λ(m)=(1+m)e-m,m=1,2,3,…
表1给出了5种不同维修水平(即m值)下,改善因子λ(m)的取值以及相应的维修费用。

表1不同维修水平m下相应改善因子及维修费用
在装备故障率函数中,令β=2,η=2,即装备的首次故障时间期望值是1.77年。装备寿命周期L=7年,保修期W=2年,延伸保修期限We=4年;不完全预防性维修间隔期T=0.33年,即每年进行3次预防性维修;为方便分析,假设每次预防性维修时间Tp=2天;故障维修时间Tf=5天,维修费用Cr=200元,每天的停机损失费用为c=40元;文中假设每年为360天。
运用文中建立的数学模型及以上的参数设置,经过计算可以得到在最小维修-不完全预防性维修组合策略下延伸保修购买决策所对应的价格区间,在不同预防性维修水平m下购买延伸保修的价格区间以及装备单位时间费效比变化如表2所示,除表中所给出的延伸保修价格区间外,在初始保修结束后,装备均由部队自主保障。

表2不同维修水平下费效比及购买决策区间
由于不完全预防性维修是在装备保修期结束后进行的,其对承制方保修成本没有影响,所以在不同维修水平下EWC的值不变。随着维修水平m的上升,单位时间内装备的费效比呈先减少后增长的趋势且Cnp/A2≤V1,因此,军方才有可能购买延伸保修服务。当延伸保修价格在表中所列的区间内时,军方和承制方才能同时获益,如当m=3时,Cw的取值范围为[600,808.06],如图3所示,理论上最合理的延伸保修价格应该是两个端点的平均值即704.03,这时,生产商利润CP= 104.03,在考虑可用度情况下军方的综合收益也为CB=104.03。

图3 m=3时的延伸保修购买决策价格区间图
当故障率函数尺度参数值以及最小维修费用Cr变化时,固定m=3,形状参数β=2和其他参数值,运用文中所提出的数学模型计算出不同数值所对应的购买延伸保修所对应的价格区间,具体结果见表3所示。

表3不同维修费用及故障率下延伸保修购买决策价格区间
当η=1时,表示首次故障时间期望为0.88年;η=2时,表示首次故障时间期望值为1.77年;η=3时表示首次故障时间期望值为2.66年。可以看出随着η的值提高,装备的可靠性是逐渐提高的。由表中的数据结果可以看出,当装备故障率过高时,EWC>EWPmax,承制方一般不会提供延伸保修服务;当Cr固定时,随着装备可靠性的增加,承制方提供延伸保修服务的最低价格即延伸保修成本(EWC)降低,而军方可接受的延伸保修最高价格EWPmax升高。所以,在初始保修结束后,是否提供延伸保修在一定程度上也可以作为判断装备可靠性的参考。可以看出,如果承制商提供的装备可靠性高,提供延伸保修可以为承制方带来巨大的利润。如在Cr=150的情况下,如果延伸保修定价为EWC和EWPmax的平均值,当η=2时,生产商利润CP=169.65;当η=3时,CP=633.4。
5 结论
延伸保修作为初始保修结束后的一种契约式的服务合同,对于军方和承制方都具有重要意义。本文在对延伸保修服务分析的基础上,提出了关于延伸保修购买决策问题的数学模型,通过示例验证了模型的有效性并给出了不同延伸保修服务价格下军方和承制方的决策以及可能存在的双方共赢
的延伸保修价格区间。为军方科学决策是否购买延伸保修以及双方合理确定延伸保修价格提供了参考方法。本文只考虑了在装备寿命周期固定时,采用最小维修-不完全预防性维修策略下的延伸保修定价问题,存在一定的局限性,在未来工作中可以针对这些问题进行深入研究。
参考文献:
[1]YEH L,PEGGO L,WAI K. An extended warranty policy with options open to consumers[J]. European Journal of Operational Research,2001(131):514-529.
[2]JACK N,MURTHY D N P. A flexible extended warranty and related optimal strategies[J]. The Journal of the Operational Research Society,2007,58(12):1612-1620.
[3]WU S M,LONGHURST P. Optimising age-replacement and extended non-renewing warranty policies in life cycle costing [J]. International Journalof Economics,2011(130):262-267.
[4]KIM C S,DJAMALUDIN I,MURTHY D N P. Warranty and discrete preventive maintenance[J]. Reliability Engineering and System Safety,2004(84):301–309.
[5]KIJIMA M. Some results for repairable systems with general repair[J]. Appl Probab,1989(26):89–102.
[6]SAHIN I,POLATOGLU H. Maintenance strategies following the expiration of warranty[J]. IEEE Trans Reliab,1996(45)220-228.
Research on Equipment Extended Warranty Purchase Decision- Making Based on Cost- Effectiveness Analysis
YANG Zhi-yuan,CHENG Zhong-hua,DENG Li-jie
(Ordnance Engineering College,Shijiazhuang 050003,China)
Abstract:Warranty is an important way to introduce manufacture’s maintenance resource into the army,and the extended warranty has significant effect on manufacturer’s warranty cost and equipment’s Life Cycle Cost(LCC). In order to make a decision for the problem whether purchasing the extended warranty,in this paper a mathematical decision model to obtain the extended warranty purchase decision-making strategy under different price interval based on the analysis of extended warranty policy by balanced the benefit of manufacturer and military is developed. The model also allows looking if there is zone of compromise yielding a win-win relationship with respect to the cost and availability of the product. At last,the model proved to be practical by the case study.
Key words:extended warranty,cost-effectiveness analysis,purchase decision-making
作者简介:杨志远(1990-),男,河北石家庄人,硕士研究生。研究方向:装备保障理论与应用。
*基金项目:国家自然科学基金资助项目(70971135)
收稿日期:2015-01-21
文章编号:1002-0640(2016)02-0018-05
中图分类号:F270
文献标识码:A
修回日期:2015-03-06
