某型多管火箭炮射击间隔优化研究

王惠方，任　杰，代　波，仲健林

（1.西北机电工程研究所，陕西　咸阳　712099；2.南京理工大学机械工程学院，南京　210094）



某型多管火箭炮射击间隔优化研究

王惠方1，任杰2，代波1，仲健林2

（1.西北机电工程研究所，陕西咸阳712099；2.南京理工大学机械工程学院，南京210094）

摘要：为提高某型多管火箭炮火力密度，对其射击间隔进行优化研究。首先，建立某型多管火箭炮刚柔耦合模型，获得定向器管口动态响应，计算火箭弹起始扰动；然后，求解火箭炮外弹道方程，采用数理统计方法得到多管火箭炮密集度估计值；其次，基于Lanczos法对多管火箭炮进行模态分析，结合火箭炮管口动态响应确定新的射击间隔；最后，将新射击间隔输入动力学模型计算，结果表明在不影响射击密集度的基础上，新的射击间隔缩短发射时间21.4%，有效地提高了多管火箭炮火力密度。

关键词：多管火箭炮，火力密度，射击间隔，动力学仿真，模态分析

0　引言

多管火箭炮火力密度是指单位时间内火箭炮发射弹丸的数量，强大的火力密度是火箭武器重要的战术技术指标［1］，合理地安排射击间隔是提高多管火箭炮火力密度的重要途径之一。文献［2-6］基于多体系统传递矩阵法和发射动力学理论，研究了射击顺序和射击间隔对多管武器系统性能的影响，文献［7-9］建立某多管火箭刚柔耦合多体系统动力学模型，提出了两管齐射的方案缩短发射时间，有效地提高了射击密集度和火力密度。本研究中某型多管火箭炮发射箱尺寸较小，两管齐射易造成弹在空中碰撞，发射掉弹或早炸的危险，因此，在不影响射击密集度的基础上，本文通过合理缩短发射间隔的方法提高火箭炮火力密度。

文中以某型多管火箭炮为研究对象，建立其动力学仿真模型，计算火箭炮发射的起始扰动；运用蒙特卡罗模拟技术和随机数生成算法产生n组随机因素的值，将n组值及起始扰动代入多管火箭炮外弹道方程，计算得到n组落点位置，数理统计获得火箭炮密集度仿真值；利用Lanczos法获得多管火箭炮模态频率特性，结合火箭炮管口动态响应确定新射击间隔，将新的射击间隔输入模型进行仿真计算，火箭炮密集度符合设计指标要求，发射时间缩短，火力密度得到增强。

1　动力学模型与起始扰动

1.1多管火箭炮动力学模型

起始扰动是指发射系统作用于火箭弹的扰动，建立多管火箭炮动力学模型，获得火箭炮定向器的振动响应，为火箭弹起始扰动计算提供参数。动力学模型包括：运发箱、摇架、上架、高低机、回转机构、轮胎、驾驶室等部件。结合梁单元和壳单元，参照多管火箭炮几何结构建立武器系统的有限元模型，轮胎及液压支腿采用非线性连接单元进行模拟，驾驶室为显示体，施以相应的质量点进行配重。为减小计算量，以非满管（8发）代替满管进行计算［10］，初始射击间隔为0.7 s，火箭炮动力学模型如图1所示。

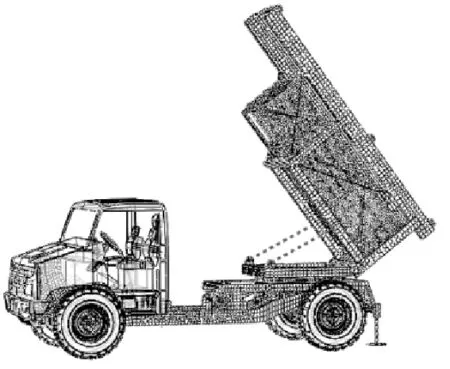
图1多管火箭炮动力学模型

利用Abaqus/explicit模块进行仿真计算，获得8枚定向器管口处弹轴坐标系下俯仰和偏航角速度、线速度、角位移响应。限于篇幅，给出第8枚定向器的角速度、线速度、角位移响应如图2~图7所示。

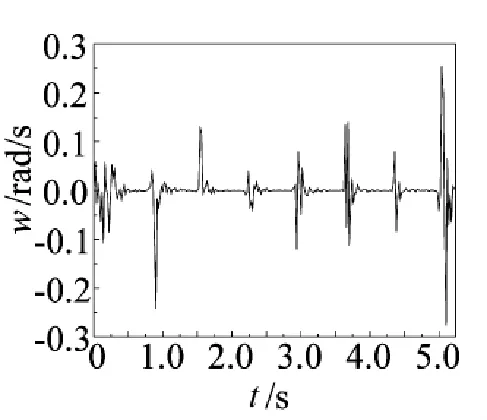
图2定向器俯仰角速度曲线

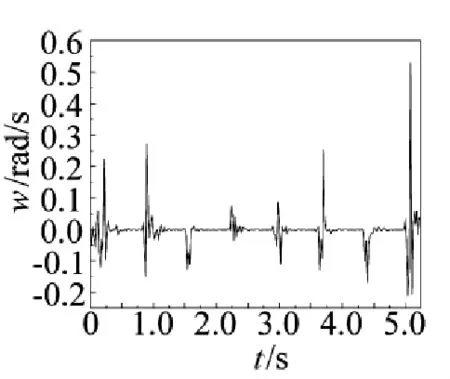
图3定向器偏航角速度曲线

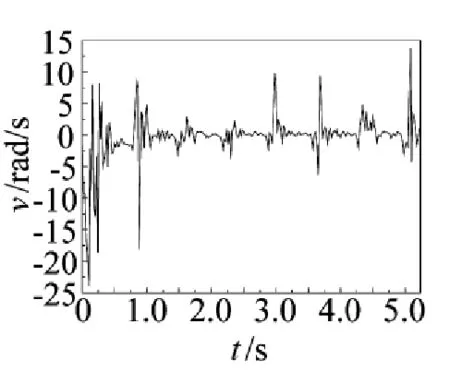
图4定向器俯仰线速度曲线

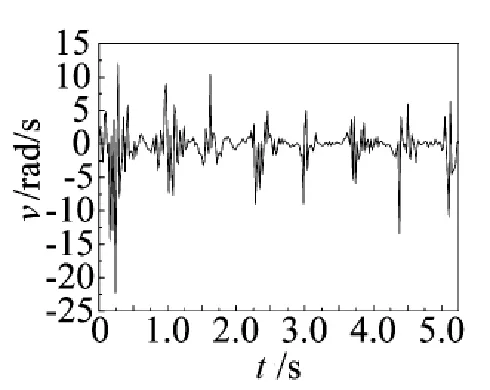
图5定向器偏航线速度曲线

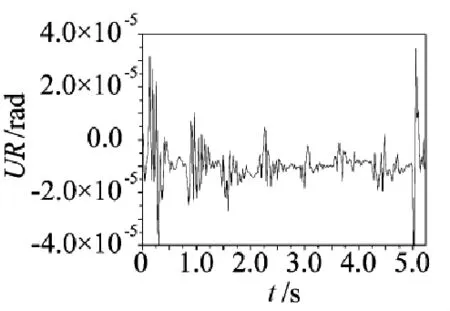
图6定向器俯仰角位移曲线

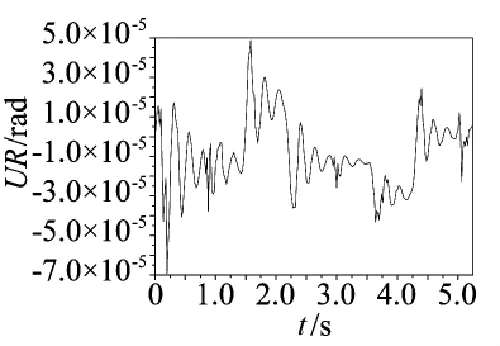
图7定向器偏航角位移曲线

1.2起始扰动计算

计算火箭弹射击密集度需要考虑的是火箭弹的起始扰动，因此需要将发射动力学模型仿真获得的火箭炮定向器的角速度、线速度、角位移转化为火箭弹的起始扰动。假设火箭弹为刚体，不考虑弹炮间隙和定向器微弯曲的影响，火箭弹半约束期运动模型如图8所示。

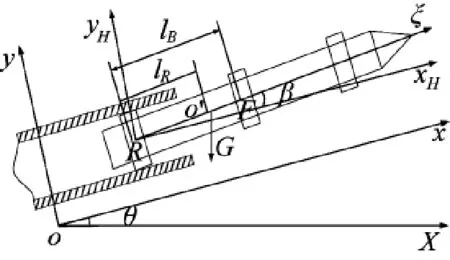
图8半约束期运动模型

火箭炮振动引起的起始扰动角速度为：

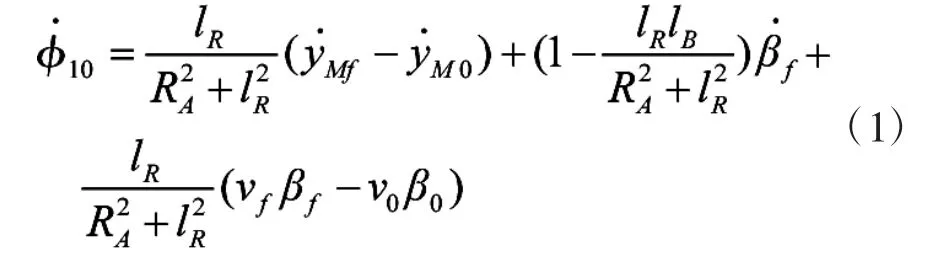
将动力学模型仿真获得定向器管口角速度、线速度、角位移代入式（1）进行计算，得到8枚火箭弹起始扰动如表1所示。

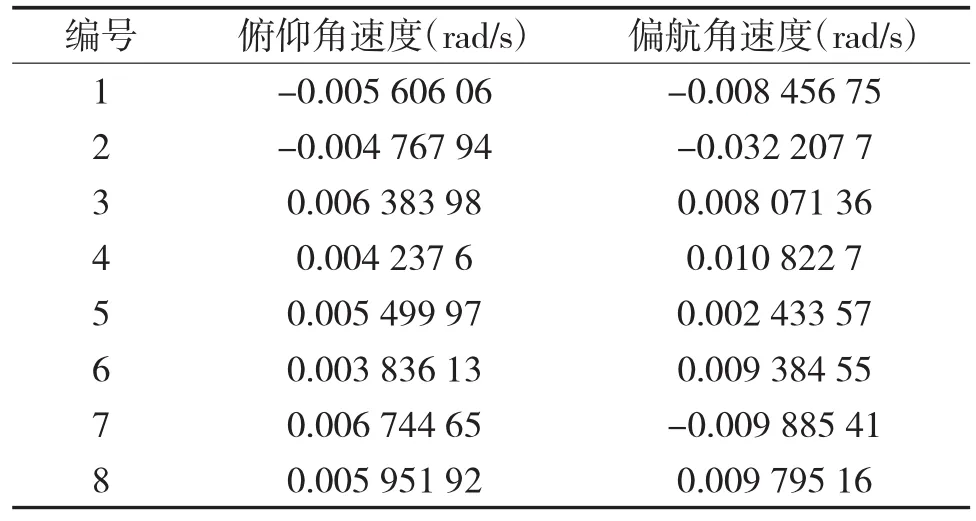
表1起始扰动计算结果

2　射击密集度仿真

射击密集度包括：立靶密集度、空炸密集度和地面密集度。本文研究多管火箭炮的地面密集度，密集度计算的总体思路为：①基于文献［11］中火箭炮外弹道方程，结合蒙特卡罗法，根据随机因素的统计特性，产生伪随机数序列；②将产生的伪随机数序列和起始扰动代入外弹道方程，求解得到火箭弹落点坐标；③重复①、②n次，直至满足蒙特卡洛法精度要求。

基于以上思路，采用Matlab建立密集度仿真系统，使用龙格-库塔法对外弹道方程进行求解，通过计算，获得了n组炸点坐标（x1，z1），（x2，z2），Λ，（xn，zn）。利用数理统计的方法，得到密集度估计值：

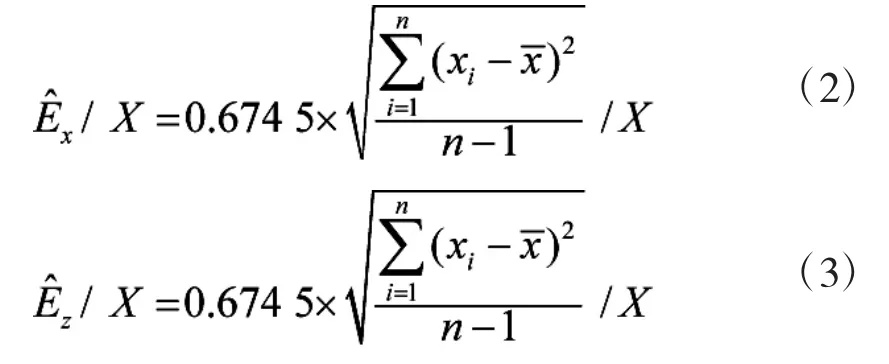
密集度仿真计算结果与设计指标对比如表2所示。密集度仿真估计值与设计指标符合较好，仿真方法的正确性得到验证。

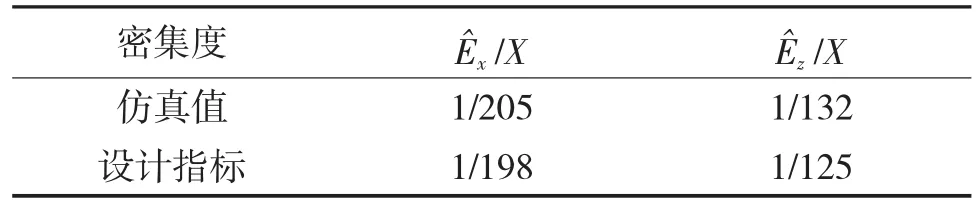
表2集度仿真与设计指标对比

3　射击间隔优化

射击频率和多管火箭炮的固有频率相近会引起共振现象，因此，建立多管火箭炮模态分析模型，基于Lanczos模态分析法获得多管火箭炮前5阶模态响应。

Lanczos法的基本步骤是选择初始向量，通过多次反迭代、正交化处理，形成m个Lanczos向量，正交和规范化系数形成一个三对角矩阵，在此基础上求得原广义特征问题前若干阶特征解。

设广义特征值问题：

KX-w2MX=0（4）

对于无刚体运动的约束系统，刚度矩阵K是实对称正定的，将K进行Cholesky分解。式（4）可改写为：

AY=μY（5）

其中：K=LLT（L为下三角阵），μ=1/ω2，A=L-1ML-T，Y=LTX。

式（5）的特征解经转换即为式（4）的解。选择初始Lanczos向量Vi，初始向量的选择应满足VTiVi=I，（I为单位阵），通过下式可将A矩阵转换为三对角矩阵：

VTAVQ=μVTVQ（6）

其中：VQ=Y

VT=V-1（7）

VTAV=T是一个三对角矩阵，则有：

VTAVQ=TQ=

由式（7）、式（8）可得：

AV=VT（9）

向量Vi+1与前两个向量Vi、Vi-1正交，式（9）表示为：

AV=βi-1Vi-1+αiVi+βiVi+1（10）

完成上述迭代，形成m个Lanczos向量Vi（i= 1，2，…，m），m为待求特征解数的2倍。

运用基于Sturm定理的二分法解式（8）得到要求阶数的特征值。式（8）不能得到全部n阶数2倍。特征值问题可表示为：

TmZ=μiZ（12）

式中：μi是由截断三对角矩阵得到的特征值。用二分法解得特征值μi后，进行反迭代可得特征向量Z，再由Y=VZ得到Y。再由X=L-TY，得到原特征问题的特征向量X，特征值=1/μi（i=1，2，…，m）。基于上述方法，得到多管火箭炮前5阶频率周期如表3所示。

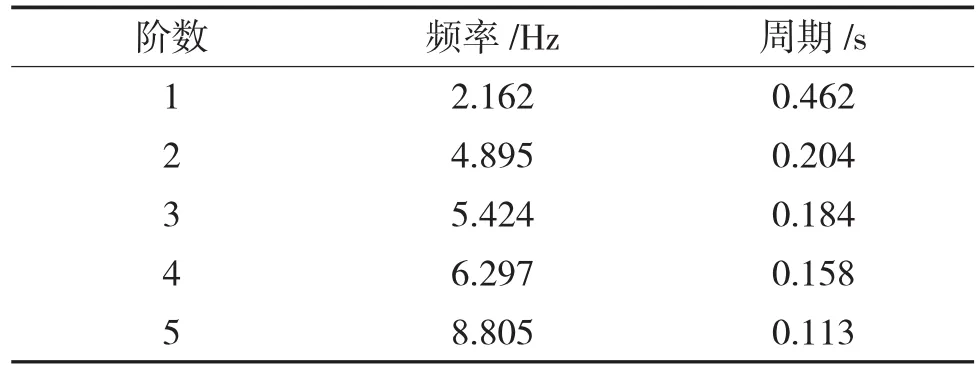
表3前5阶频率周期表

多管火箭炮初始射击间隔为0.7 s，火箭弹出筒时间约为0.2 s，由图2～图5中定向器管口动态响应可知在火箭弹出筒后0.2 s多管火箭炮已趋于平稳，可以发射下一枚火箭弹，综合考虑多管火箭炮模态特性和动态响应，将射击间隔缩短至0.55 s。

4　新射击间隔密集度仿真

将新射击间隔输入多管火箭炮动力学模型，参照第2节中研究方法进行仿真计算，仅给出第8枚定向器的俯仰、偏航角速度响应对比如图9～图10所示，给出8枚弹道起始扰动如表4所示，计算得到新射击间隔下多管火箭炮射击密集度如表5所示，可见新的射击间隔缩短发射时间21.4%，有效增强其火力密度，且密集度仍在设计指标要求范围内。

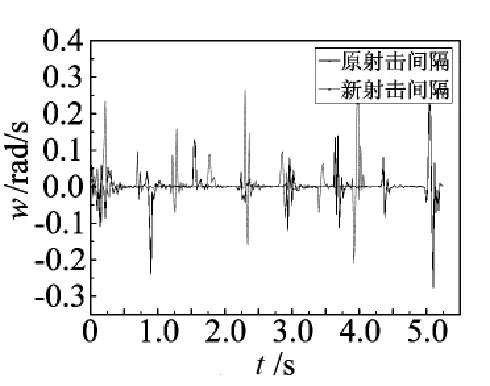
图9定向器俯仰角速度对比曲线

图10定向器偏航角速度对比曲线

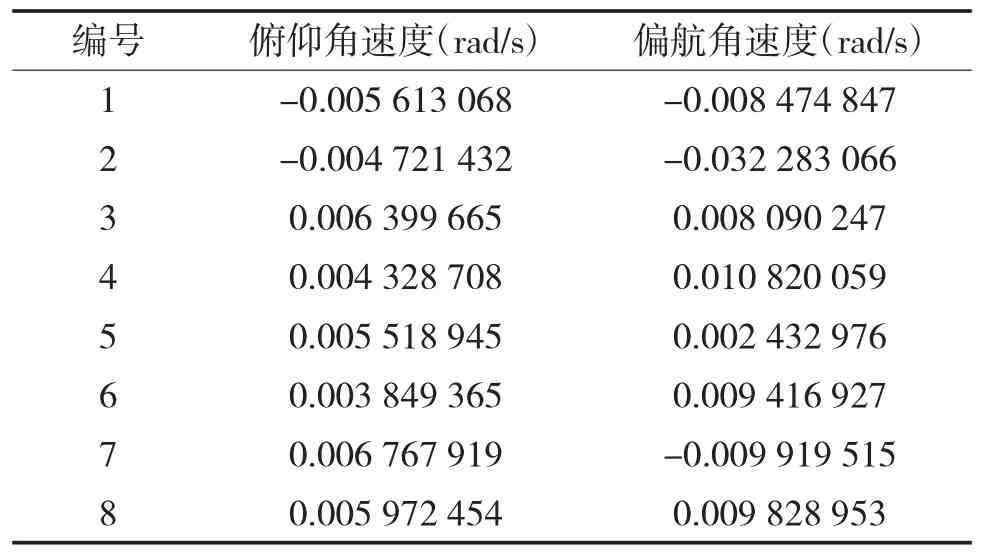
表4新射击间隔起始扰动计算结果

5　结论

本文利用有限元方法建立了某型多管火箭炮发射动力学模型，仿真分析得到定向器管口动态响应，基于火箭炮半约束期运动模型求得其起始扰动，进而计算得到原始射击间隔下的射击密集度估计值，综合考虑火箭炮模态特性和动态响应确定新的射击间隔，仿真计算新的射击间隔下的射击密集度，表明在不影响射击密集度基础上，射击时间缩短21.4%，火力密度得到提高，研究方法能够指导多管火箭炮的设计与研制。

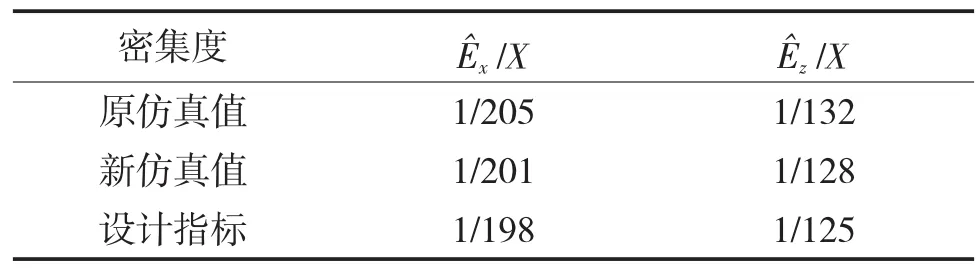
表5密集度仿真与设计指标对比

参考文献：

［1］娆昌仁.火箭导弹发射动力学［M］.北京：北京理工大学出版社，1996.

［2］芮筱亭，王国平，陆毓琪，等.提高多管火箭射击密集度新技术［J］.兵工学报，2006，27（2）：301-305.

［3］王国平，芮筱亭，陈卫东，等.应用最大熵法的多管火箭密集度仿真［J］.弹道学报，2007，19（2）：13-15.

［4］王国平，芮筱亭.遗传算法在优化多管火箭射序中的应用［J］.弹箭与制导学报，2006，26（3）：146-147，150.

［5］贺军义，芮筱亭，王国平，等.提高多管火箭射击密集度设计技术研究［J］.振动工程学报，2011，24（6）：676-681.

［6］王国平，芮筱亭，陆毓琪，等.射序对多管火箭武器性能影响［J］.南京理工大学学报（自然科学版），2004，28（4）：364-368.

［7］于存贵，乐贵高，马大为，等.提高船载火箭炮射击密集度研究［J］.兵工学报，2007，28（6）：646-650.

［8］王雷，马大为，于存贵，等.提高多管火箭炮发射火力密度研究［J］.火力与指挥控制，2012，37（4）：18-20.

［9］朱忠领，马大为，李自勇，等.2枚火箭同时发射时火箭炮动态特性分析［J］.弹道学报，2006，18（3）：65-67.

［10］王国平，芮筱亭，陈卫东，等.减少多管火箭武器试验用弹量仿真技术［J］.兵工学报，2004（6）：786-789.

［11］宋否极.枪炮与火箭外弹道学［M］.北京：兵器工业出版社，1993.

Optimization Research of Firing Interval for MLRS

WANG Hui-fang1，REN Jie2，DAI Bo1，ZHONG Jian-lin2
（1. Northwest Institute of Mechanical Engineering，Xianyang 712099，China；2. School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

Abstract：To improve firing density level of MLRS，optimization research of firing interval is applied. Firstly，the rigid-flexible-coupling model of MLRS is built to obtain the dynamic response of the launch guider muzzle and the rocket initial disturbance is calculated. Secondly，the equation of exterior ballistic is solved and the estimate of dispersion is obtained with mathematical statistic method. Thirdly，modal analysis for MLRS is carried out based on Lanczos algorithm and the new firing interval is proposed combined with the dynamic response obtained above. Finally，substitute the new firing interval into the model of MLRS，the results show that the new firing interval shorten the firing time by 21.4% and improve the firing density effectively without affecting the dispersion of the MLRS.

Key words：MLRS，firing density，firing interval，dynamics simulation，modal analysis

作者简介：王惠方（1972-），男，河南清丰人，研究员级高工。研究方向：火箭炮武器系统。

收稿日期：2014-12-27

文章编号：1002-0640（2016）02-0104-04

中图分类号：TJ714

文献标识码：A

修回日期：2015-03-01