战斗机“滚筒”机动的末端规避效果*

谢新辉，张学斌，李　飞，汪　洋

（1.空军工程大学航空航天工程学院，西安　710038；2.解放军93286部队，沈阳　114141）



战斗机“滚筒”机动的末端规避效果*

谢新辉1，张学斌2，李飞1，汪洋1

（1.空军工程大学航空航天工程学院，西安710038；2.解放军93286部队，沈阳114141）

摘要：针对在线实时计算末端规避策略飞行员操纵难度大、规避效果差的现状，研究了战斗机HGB机动的末端规避效果。首先分析了HGB机动末端规避的原理；其次建立了HGB机动末端规避的数学模型；最后基于典型作战场景，研究了比例导引系数、导弹最大可用过载、制导回路延迟时间和弹目接近速度对HGB机动效果的影响，仿真得到导弹的脱靶量随HGB的机动角速度均呈先增大后减小的趋势。研究结果为飞行员选择合适的角速度范围做HGB机动末端规避时具有参考价值。

关键词：滚筒机动，脱靶量，末端规避，角速度

0　引言

末端规避是飞机防御导弹攻击的重要手段，对提高战斗机生存概率具有重要意义，末端规避问题同时也越来越受到广泛关注。早在1975年，G.Carpenter和M.Falco建立了飞机最优机动规避模型［1］；1996年，Shaw将SQP算法引入到末端规避中，并对影响导弹脱靶量的因素进行了分析［2］。Li于2006年得到了垂直面内的飞机末端规避问题的全局最优解［3］。

目前，战斗机末端机动规避策略大多是在线实时计算的，在战斗机采用自动驾驶的情况下或对于无人机来讲，实时计算的规避策略将具有较高的实用价值，但在飞行员操纵飞机规避时，考虑到飞行员的反应特性，这种实时的在线计算规避策略的效果将大大降低。

对此，Imado［4］对“滚筒”（High-g Barrel Roll，HGB）机动的规避效果进行了研究，本文在文献［5-8］的基础上，分别对不同导引参数、不同导弹最大过载、不同延迟特性和不同接近速度下导弹脱靶量与角频率的关系进行了研究分析，以得到HGB末端规避的最佳实施参数。

1　战斗机HGB末端规避原理分析

1.1末端规避的基本原理

末端规避是战斗机在导弹攻击的末端，通过载机的机动使得导弹因为超出限制条件而无法实现理想的弹道，继而无法命中目标。其本质是基于闭环控制系统存在动态误差的原理，通过不同的机动时机、方法和过载，使其动态误差不断增大，增大导弹的脱靶量，降低其命中概率。

导弹攻击目标的过程可以用图1的反馈闭环控制系统来描述，导弹能够命中目标的条件就是该闭环过程能够在误差允许范围内运行，这就为系统中每个环节提出了限定条件，若其中一个环节超出了限定范围，即有可能使得导弹无法命中目标。战斗机末端规避导弹攻击任务的实现即是战斗机针对该闭环系统中各个环节的弱点，综合利用各种手段使得其在运行过程中超出其限定范围，从而阻止导弹的命中目标。

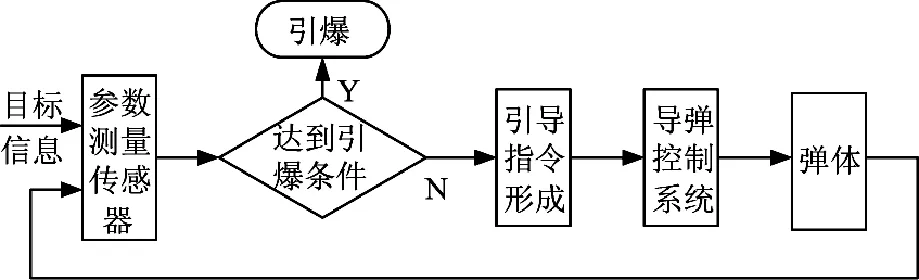
图1导弹攻击目标反馈闭环

1.2战斗机HGB末端规避原理

目前，空空导弹的导引律大多为比例导引及其变化形式，其基本机理是：导引头通过测算导弹-目标的视线角速度，控制导弹的俯仰和偏航角速度成比例地增大，从而构成对目标的前置跟踪。由此，当目标在导弹达到跟踪时，突然做方向机动时，则视线也将向反方向偏转，视线角速度变为负值，导弹原来构成的前置角由此变成了“后置角”。此时，导弹为构成新的前置角，必须回转，以消除“后置角”。若设导弹的前置角为10°，那么当目标做±5°的机动时，导弹就须有来回修正30°，才能构成新的前置跟踪。

因此，战斗机的HGB机动将使导弹的制导控制系统周期性地改变跟踪指令，当指令的变化频率超出系统的带宽时，则会导致其跟踪结果的发散，从而无法及时跟踪目标。尤其是导弹在执行这种周期性跟踪指令时，需要操纵舵面做高效的周期性偏转，这对于导弹弹体的结构强度和操纵效能具有较高的要求。即使导弹修正前置角所需的过载指令在其可用过载限制范围之内时，但要求其舵面在短时间内修正较大的过载，也是很困难的。由此可见，战斗机用HGB变载机动造成导弹跟踪的困难，并不是迫使导弹超载，而是造成导弹不能按理想弹道跟踪，从而增大遭遇时的脱靶量。

2　 HGB末端规避的数学模型

2.1坐标系的选取

为描述战斗机、导弹以及相对位置和运动学、动力学特性，建立数学模型，就必须选取适当的坐标系。为此，本文选取地理坐标系（OXYZ）为基准坐标系。其坐标原点选取在导弹的质心上，Xe轴沿该点的经线的切线方向指向北方，Ye轴沿该点的纬线的切线方向指向西方，Ze轴根据右手定则确定指向天，简称北-西-天坐标系。

2.2 HGB的数学模型

HGB是一种同时在垂直和水平面内作S形运动的一种机动。该机动具有周期性的特点，其机动指令操作简单，飞行员只需通过周期性的拉杆和压杆即可实现该机动。该机动表现为：战斗机在垂直平面内做圆周运动，在X方向上作匀速运动。如图2所示，其机动模型可用下式描述：

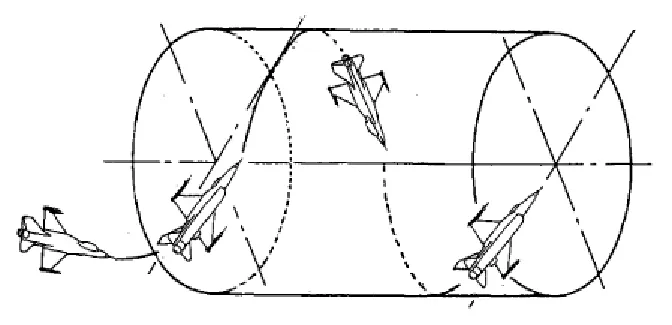
图2 HGB机动

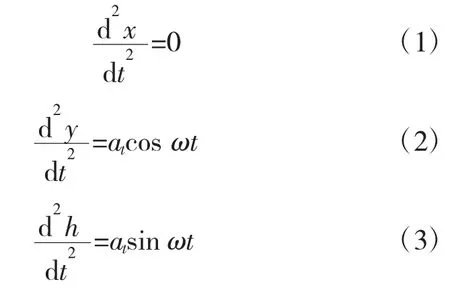
式中，at为战斗机的横侧向过载，ω为圆周运动的角速度。

由式（1）~式（3）可得战斗机做HGB机动时在速度表达式为：

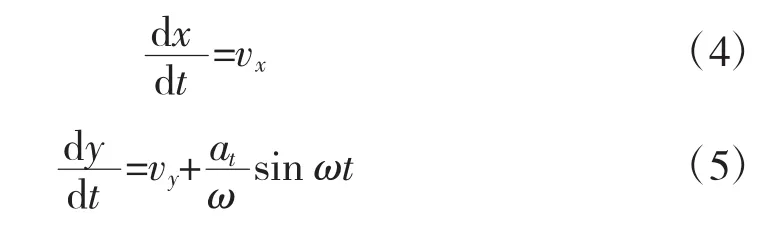
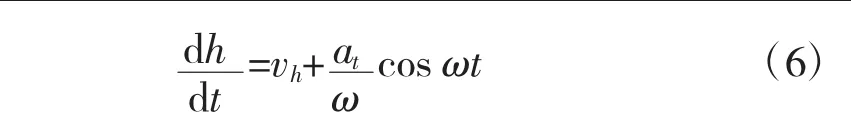
则其机动轨迹可以描述为：

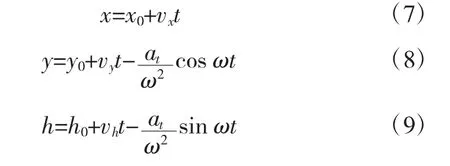
式中，（x0，y0，h0）为机动开始时的初始位置，vx，vy，vh为机动开始时的战斗机在3个坐标轴上的初始速度。

2.3导弹运动模型

忽略地球扁率和自转和风的影响，将导弹看成质点，建立导弹运动的三自由度模型。

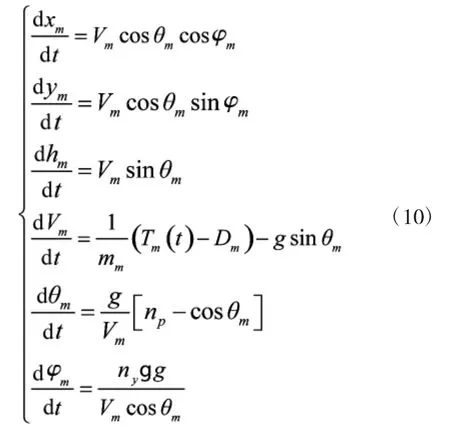
式中，xm，ym，hm，Vm，θm，φm，np，ny分别为导弹的三维坐标、速度、航迹倾角、航迹偏航角、导弹俯仰和偏航过载，Tm为导弹发动机推力，Dm为导弹受到的空气阻力。

考虑到机载导弹告警系统内的脉冲多普勒雷达的探测范围和导弹发动机的工作时间，可以认为，在对来袭导弹进行跟踪时，导弹的发动机已经停止工作，即：

Tm（t）=0（11）

导弹的阻力Dm可按下式求取：

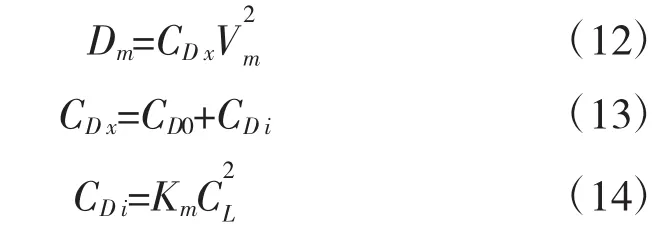
式中，CD0为导弹零升阻力系数，CD i为诱导阻力系数，Km为升阻比，CL为升力系数。

同时将导弹的制导控制系统等效为一个二阶阻尼系统和一个惯性系统，其控制系统传递函数模型如式（15）所示：

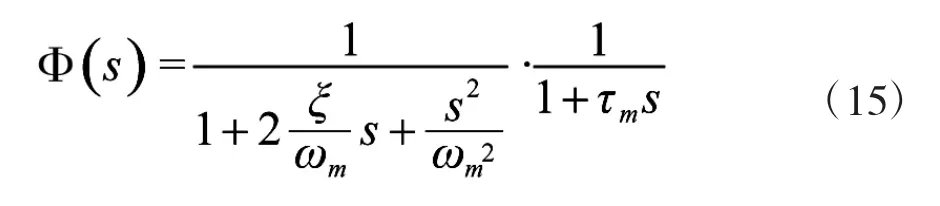
式中，ξ为阻尼比，ωm为自然频率，τm为制导控制系统的延迟时间。

由于控制制导系统的延时特性，导弹实际俯仰、偏航过载与俯仰、偏航过载指令关系如下：

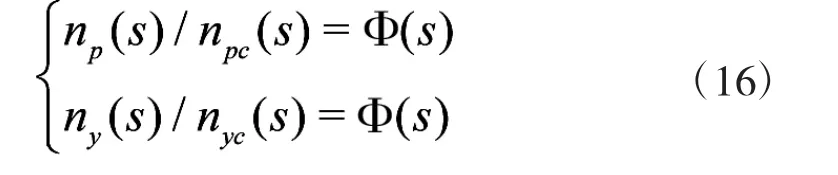
式中，npc，nyc为导弹的俯仰和偏航过载指令，

2.4导弹导引模型

比例导引法是要求导弹速度矢量的转动角速度与视线的转动角速度成比例。在目前的空空导弹中，常常采用比例导引法对其进行导引控制。

设apc表示俯仰方向的加速度指令，ayc表示偏航方向的加速度指令，则

eap、eay分别为俯仰轴和偏航轴的单位矢量，其定义如下：

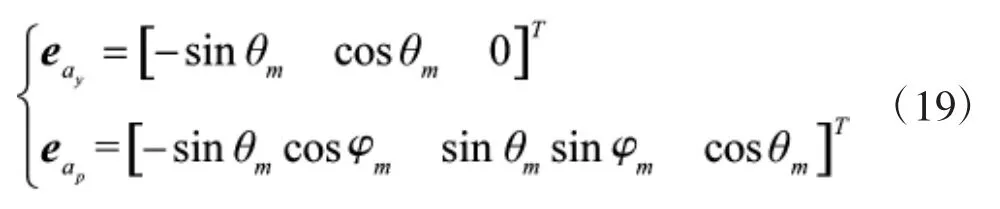
npc和nyc可由下式求解：

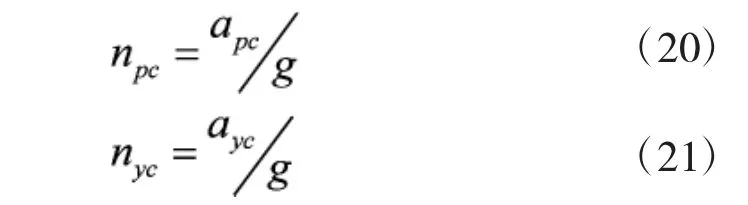
同时，由于受到结构和材料强度的限制，导弹由最大可用过载的限制，npc和nyc可由下式求解：

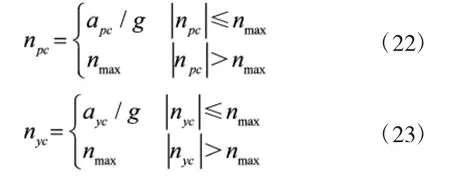
3　 HGB末端规避效果仿真分析

为了分析影响HGB机动规避效果的各种因素，分别对不同导引参数、不同导弹最大过载、不同延迟特性和不同接近速度下导弹脱靶量与角频率的关系进行了仿真。导弹与载机的初始状态参数如下页表1所示。

导弹的气动参数设为：CD0=0.5，Km=0.05，CL=3；阻尼比取0.7，自然频率取为18rad/s，延迟时间为0.3 s。

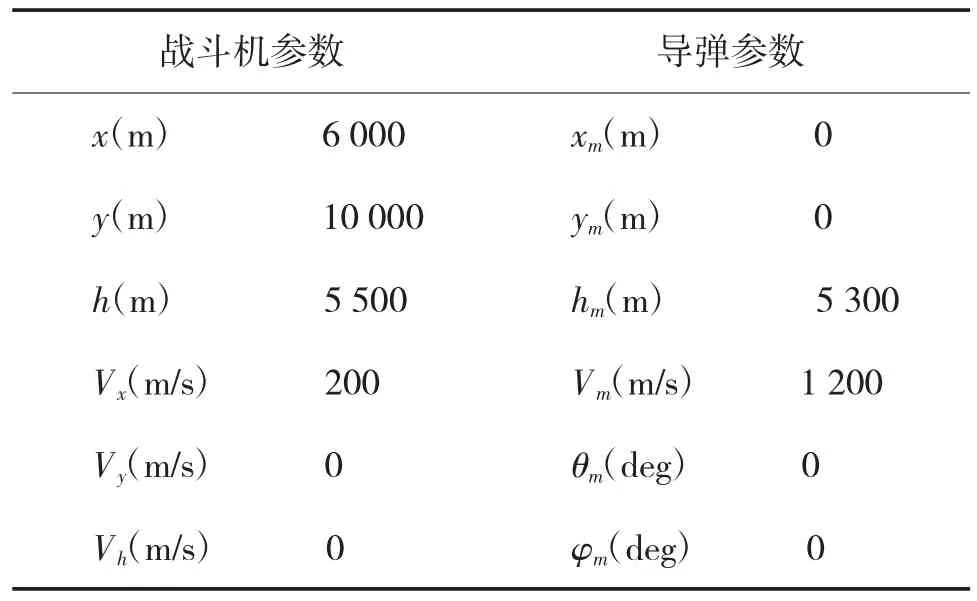
表1初始参数

①不同比例导引系数下HGB规避效果仿真

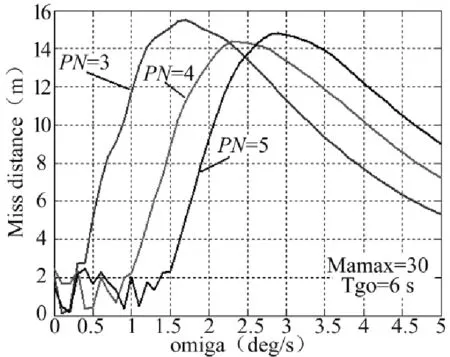
图3不同比例导引系数下ω-MD曲线

从图3可以看出，在机动角速度一定的情况下，导弹的脱靶量随着比例导引系数的增大呈现先减小后增大的趋势；也就是说，在脱靶量一定的情况下，HGB机动角速度随着比例导引系数的增大而增大；其最优的机动角速度在［1.3，3.6］之间。

②不同最大可用过载下HGB规避效果仿真

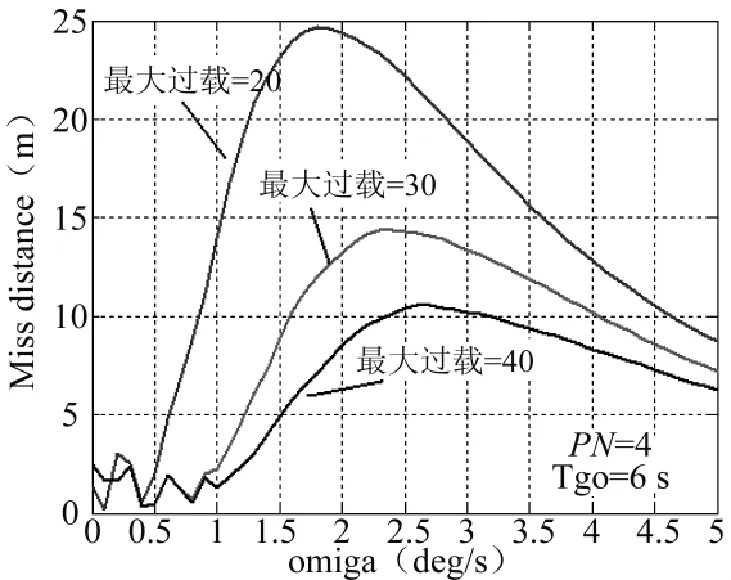
图4不同最大可用过载下ω-MD曲线

从图4可以看出，随着导弹可用过载的增大，HGB机动角速度也呈增大的趋势，但导弹的最大可用过载对于导弹的脱靶量有很大影响，可用过载越大，导弹的脱靶量越小，因此，HGB机动在规避具有高机动能力的导弹时，效果较差；其最优的机动角速度在［1.3，3.7］之间。

③不同制导回路延迟时间下HGB规避效果仿真

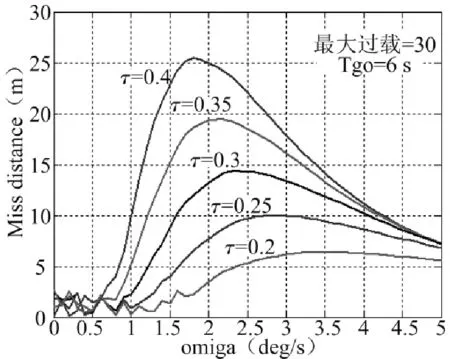
图5不同制导回路延迟时间下ω-MD曲线

从图5可以看出，导弹制导控制回路的延迟时间对于HGB的规避效果也有很大影响，延迟时间越小，HGB的规避效果越差，其最优的机动规避角速度随着延迟时间的减小而增大；其最优的机动角速度在［1.5，3］之间。

④不同接近速度下HGB规避效果仿真

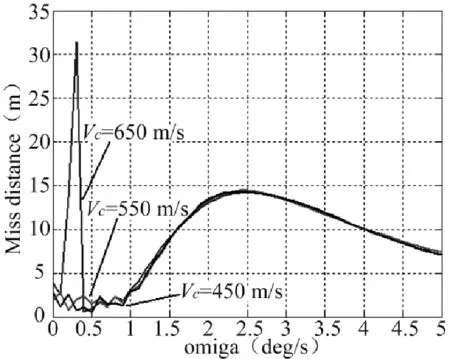
图6不同接近速度下ω-MD曲线

从图6可以看出，初始的弹目接近速度对于HGB的规避效果的影响不大，其最优的机动角速度在［2，3.5］之间。综上所述，在不同参数下仿真得到角速度和脱靶量的关系，为使脱靶量达到理想值，最优的机动角速度应取在［2，3］之间。

4　结论

本文旨在研究战斗机HGB机动策略的末端规避效果，对HGB机动末端规避导弹攻击的机理进行分析，通过仿真研究影响HGB机动规避效果的各种因素，由此确定HGB机动末端规避的理想参数；仿真结果表明，在不同的参数下导弹的脱靶量随HGB机动角速度呈先增大后减小的趋势，最佳的HGB机动角速度应在［2，3］（rad/s）范围内。

参考文献：

［1］CARPENTER G，FALCO M.Analysis of aircraft evasion strategies in air-to-air missile effectiveness models［R］.

Grumman Aerospace Corporation，1975.

［2］ONG S Y，PIERSON B L. Optimal planar evasive aircraft maneuvers against proportional navigation missiles［J］. Journal of Guidance Controland Dynamics，1996，19（6）：1210-1215.

［3］LI J，WU J H，KANG S G. Learning evasive maneuvers using genetic-annealing algorithms［C］// Proceedings of the 6th World Congress on Intelligent Control and Automation，Dalian，China，2006.

［4］IMADO F，KURODA A. Engagement tactics for two missiles against an optimally maneuvering aircraft［J］. Journal of Guidance Control and Dynamics. 2011，34（2）：574-582.

［5］JUNG B，KIM K S，KIM Y. Guidance law for evasive aircraft maneuvers using artificial intelligence［C］// AIAA Guidance，Navigation，and Control Conference and Exhibit，2003.

［6］IMADO F，MIWA S. Missile guidance algorithm against high-g barrel roll maneuvers［J］. Journal of Guidance Control and Dynamics，1994，17（1）：41-43.

［7］TAKANO H. Optimal flight trajectory and aerobatic maneuvers against missiles［C］// 2004 5th Asian Control Conference，2004.

［8］AKDAG R，ALTIAR D T. A comparative study on practical evasive maneuvers against proportional navigation missile［C］//AIAA Guidance Navigation and Control Conference and Exhibit，San Francisco，2005.

Research on Effects of Fighter HGB Maneuvering Terminal Evasion

XIE Xin-hui1，ZHANG Xue-bin2，LI Fei1，WANG Yang1
（1. School of Aeronautics and Astronautics Engineering College，Air Force Engineering University，Xi’an 710038，China；2. Unit 93286 of PLA，Shenyang 114141，China）

Abstract：In view of the current situation that terminal evasion strategy of online real -time calculation control big difficulty and poor effect，and the effect of fighter HGB maneuvering terminal evasion is researched. Firstly，the principle of HGB maneuvering terminal evasion is analyzed. Secondly，the mathematic model of HGB maneuvering terminal evasion is set up. Finally，the influence of proportional navigation coefficient，most available overload，guidance loop delay time，missile-target approach speed to the effect of HGB maneuvering terminal evasion based on a typical combat scene. The simulation shows that the missile distance becomes bigger firstly and then becomes smaller as the change of angle rate on the various parameters. The results provide pilots reference when select suitable the range of angle rate to make HGB maneuvering terminal evasion.

Key words：HGB maneuvering，miss distance，terminal evasion，angle rate

作者简介：谢新辉（1992-），男，江西抚州人，硕士生。研究方向：航空火力指挥控制与战术引导。

*基金项目：国家自然科学基金资助项目（61472441）

收稿日期：2014-12-27

文章编号：1002-0640（2016）02-0097-04

中图分类号：TJ85，TP391

文献标识码：A

修回日期：2015-03-01