基于ADAMS的垂直摇臂式喷头多体动力学建模与优化

汤　跃,赵　进,陈　超

(江苏大学 流体机械工程技术研究中心，江苏 镇江　212013)



基于ADAMS的垂直摇臂式喷头多体动力学建模与优化

汤跃,赵进,陈超

(江苏大学 流体机械工程技术研究中心，江苏 镇江212013)

摘要：以Nelson SR100型垂直摇臂式喷头为对象，针对现有垂直摇臂式喷头动力学性能的研究存在忽略摩擦因素、过于简化模型等问题，基于虚拟样机软件ADAMS建立了垂直摇臂式喷头的动力学仿真模型，综合考虑摇臂与转轴、喷管与水管密封等部位实际的摩擦情况，以试验数据确定各部件之间的实际摩擦因数。针对垂直摇臂式喷头的垂直上下摆动、水平左右步进旋转这两个主要动作，运用STEP函数构建一个完整周期非自由与自由运动时间段内喷头导流器所受水平与垂直力的模拟函数进行动力学仿真。最后通过换向仿真，模拟实际摇臂在换向过程中，摆动杆对限位板的接触碰撞力的大小。以接触碰撞力最大值最小为目标函数，对上述接触碰撞力最大值进行优化，将影响换向顺利程度的换向杆长度等因素作为约束条件，优化后的最大碰撞力较优化前减少了55.9%。其动力学仿真结果可以为垂直摇臂式喷头的结构强度分析与疲劳寿命优化等相关动力特性的进一步分析及喷头动力学特性的设计提供基础。

关键词：垂直摇臂式喷头；摩擦因数；动力学仿真；参数化建模；碰撞力优化

0引言

摇臂式喷头是广泛应用于农业防旱灌溉及工业降尘的重要技术装备[1]。垂直摇臂式喷头和水平摇臂式喷头相比，其主要优点在于摇臂不直接撞击喷管，运行稳定可靠及喷水均匀度高等，因而在国内外工农业领域获得了非常广泛的应用[2]。B.M.列别捷夫[3]等分析研究了摇臂的运动学特征。陈雷[4]等从动力学角度研究了摇臂式喷头的力学性能，并用计算机进行了数值求解。王祺铭[5]等利用ANSYS/LS-DYNA软件对摇臂式喷头摇臂碰撞过程进行了数值模拟。李红[6]等运用ANSYS软件对垂直摇臂式喷头进行了有限元分析，并对摇臂的疲劳寿命可靠性进行了分析。汤攀[7-8]等运用高速摄影的方法对摇臂式喷头的运动规律进行了详细的试验研究，总结了喷头关键部件对水量分布均匀性的影响权重。但是，有限元分析研究手段中存在忽略考虑相对旋转运动摩擦因素的缺陷[9-10]，以及实际碰撞受力的计算存在困难等问题。本文探讨采用虚拟样机技术，基于多体动力学分析软件MSC.ADAMS对Nelson SR100型垂直摇臂式喷头进行动力学分析，并在此基础上对关键零部件特性进行优化仿真。

1工作原理与受力分析

1.1　工作原理

垂直摇臂式喷头的工作原理：高压水从喷嘴喷出冲击到导流器的一侧，导流器上弯曲叶片结构将射流的冲击力转变成摇臂向下的竖直力和沿着喷头根部轴承旋转的水平力；此时摇臂克服配重和摩擦阻力向下旋转运动，同时整个喷头向一侧产生一定角度的旋转运动；摇臂向下运动时，其平衡配重升高，重力势能增加，然后在其与摇臂轴平衡配重重力矩的联合作用下，摇臂返回，重力势能转变为转动动能，再次切入射流，重复以上过程。当换向杆与限位器接触时，换向机构反转传动杆，驱动摇臂转换固定的角度，此时水流冲击导流器对称的另一侧，水平力方向相反，喷头开始朝另一侧运动；循环往复，实现自动换向喷洒的功能。

1.2　导流器受力

如图1所示：从喷嘴喷出的高压水流冲击导流器斜面，产生的冲击力可以分解成水平方向的力Fh和垂直导流器弯曲叶片部分的力Fd，Fd可以分解成使摇臂上下摆动的力Fv和沿着直线段方向的推力Fr。Fv提供摇臂上下翻转摇摆的驱动力，Fh成为克服喷头与水管密封摩擦促使喷头旋转一个小角度的驱动力。根据动量定理可以求出[2]

Fv=2p(d0-nb)h2sinα2

(1)

其中，p为喷嘴压力(Pa)；d0为射流直径(m);n为射流淹没的叶片数，n=4;b为叶片厚度(m);h2为导流器弯曲段叶片宽度(m);α2为叶片出水角(°)。

图1　导流器受力示意图

1.3　步进角度

整个喷头在水平力Fh的作用下会绕旋转轴步进一个角度θ，其大小根据文献[7]试验结果建立步进角度的公式为

(2)

其中，p为喷头的工作压力(kPa)；p0为大气压力(kPa)；b1为导流器叶片弯曲段宽度(mm)；D为喷嘴直径(mm)。

1.4　摇臂周期

摇臂的运动时间分为在与水接触的非自由运动时间和与射流分离的自动摇摆运动时间[7]，其计算公式为

T=t+T1=

(3)

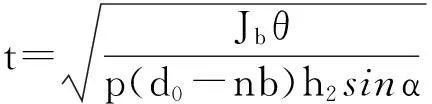
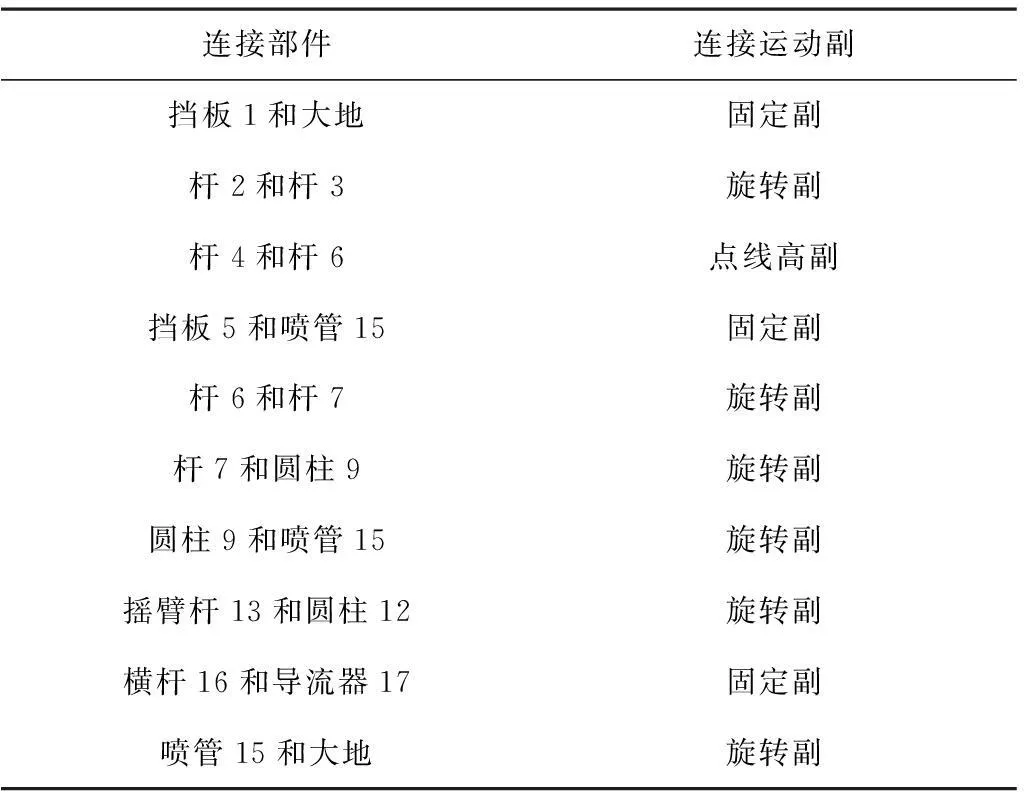
李红、刘振超[6]、汤攀[7]等针对垂直摇臂式喷头的非自由、自由运动时间、频率、摆动角等规律采用高速摄影和应力传感器贴片的方式，测得了Nelson SR100型垂直摇臂式喷头的运动规律参数。仿真采用的喷头的参数为：喷嘴口径大小15.2mm，配重位置为8.5mm，工作压力0.3MPa，喷头仰角43°。实际喷头受一次作用力的水平步进角度为3.9°。在此种工况下喷洒试验驱动力和摇臂运动时间情况测试结果如表1所示。

表1　驱动力和周期实验表

2多体动力学原理与建模

2.1　多体动力学分析原理

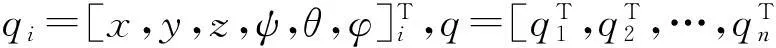
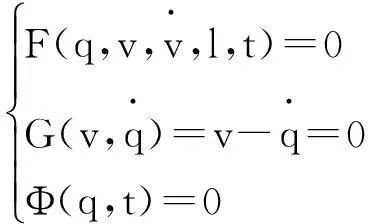
(4)

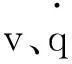
2.2　样机建模

由于ADAMS软件本身自带的实体建模功能较弱，因而最常见的做法是在三维软件中建好三维实体模型，再导入到ADAMS中去，但是导入的实体模型将不能够进行参数化分析。因而，本文的建模采用ADAMS参数化建模和三维软件混合建模的方式[15]，利用参数点作为基础构建样机的摇臂和弹簧等部件，不需要参数化的喷腔部分采用SolidWorks软件建模。虚拟样机建模完成之后的图样如图2所示。运动部件间的间接关系如表2所示。

2.3　载荷和摩擦的确定

在定义好相关运动部件之间的连接关系之后，需要定义有相对运动的部件之间的摩擦力，以及可能发生碰撞的部件之间的碰撞参数。其中，导流器受冲击力的数据采用以上试验测得的水平和竖直方向力，进行多次仿真，根据摇臂单次摆动周期来调节摇臂杆和圆柱之间摩擦因数的大小，直至符合实际的摇臂运动周期。考虑到求解函数的连续性，Fv与Fh的添加采用STEP函数，在非自由运动时间下持续对导流器的水平和垂直方向作用。在摇臂自由摇摆时间内，力则失效。单个周期下，Fv的构造函数为

(5)

Fv的构造函数为

(6)

垂直作用力的函数曲线如图3所示。

1.限位挡板　2.转向杆　3.支撑轴　4.与弹簧连接的转动杆

连接部件连接运动副挡板1和大地固定副杆2和杆3旋转副杆4和杆6点线高副挡板5和喷管15固定副杆6和杆7旋转副杆7和圆柱9旋转副圆柱9和喷管15旋转副摇臂杆13和圆柱12旋转副横杆16和导流器17固定副喷管15和大地旋转副

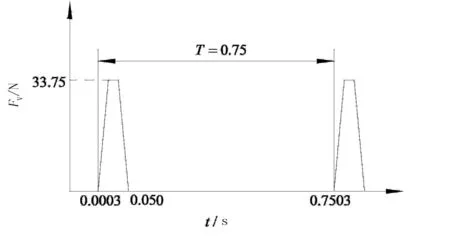
图3　垂直作用力函数图

接触采用IMPACT函数，对于一般的碰撞过程，相关参数采用默认值。设置测量，测量的内容有摇臂杆和圆柱之间的旋转角，转动杆和挡板之间接触碰撞力的大小。设置传感器来测试一次摇摆过程的时间，具体的测试方法为检测摇臂和圆柱之间的旋转角；当其旋转角再次为0时，记录整个运动的时间，此时间长即为摇臂单个运动周期。

3仿真计算

3.1　摆动仿真

设置仿真求解时间为5s，步长为500步，求解器选择Gill积分求解器，通过反复修正摇臂和圆柱之间旋转副的摩擦因数定义，使摇臂运动周期接近实际试验测试得到的摇臂周期。此时可以认为：摩擦因数的定义符合实际情况，静摩擦因数为0.02，动摩擦因数为0.01，实际单个周期垂直方向上摇摆运动的曲线图如图4所示；单个摇摆周期时间为0.753 3s，与实际测得的0.75s，误差在1%以内。

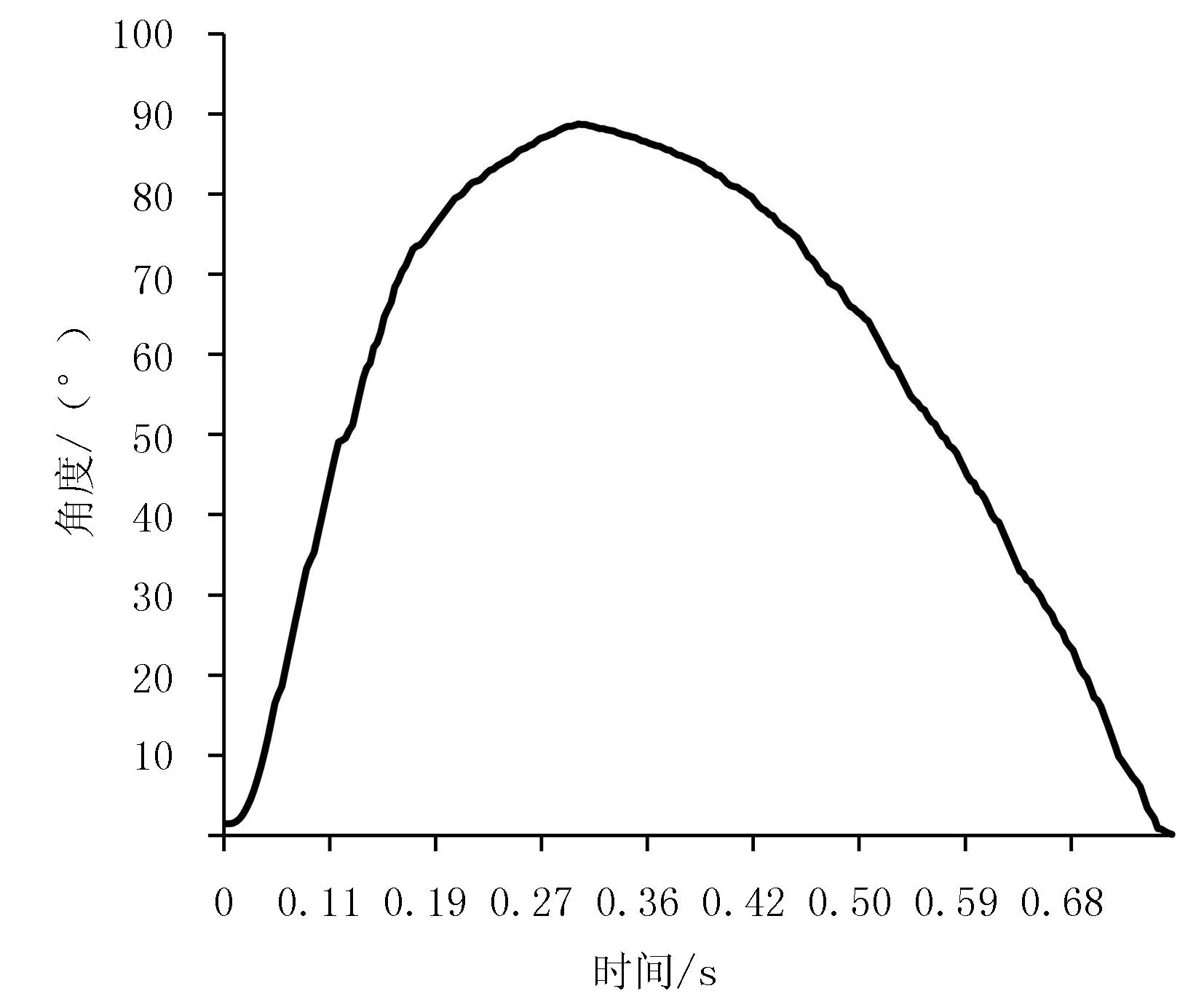
图4　单周期垂直方向摇臂旋转角度曲线图

根据试验测试结果，来调节喷枪和大地之间旋转副的摩擦因数，使其单次步进角度接近试验测试结果，控制误差在5%以内，得到喷枪和大地之间旋转副的静摩擦因数为0.1，动摩擦因数为0.05。实际的单次水平步进角度3.7°，与试验结果3.9°误差为5.1%，仿真如图5所示。

图5　单次水平步进角度图

3.2　接触碰撞仿真

当摇臂旋转了一定人为设定的喷洒角之后，杆和挡板接触，此时在水平冲击作用力Fh作用下，弹簧翻转，导流器所受水平力方向反转，此时喷头向相反方向运动。测得弹簧的刚度为0.3N/mm，在偏向一边时候的常态位置，其初始位移为3mm。通过反转碰撞仿真，可以由ADAMS测得杆件和挡板之间的碰撞力的大小数值曲线，图6所示最大碰撞力为76.54N。

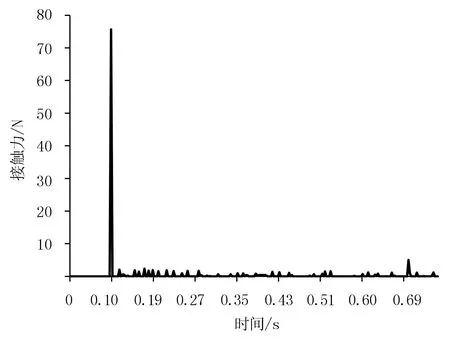
图6　碰撞力仿真数值曲线

4碰撞力的优化

4.1　参数化建模

转动杆和挡板之间碰撞力的大小可以用来衡量摇臂换向顺利程度。在长期交替碰撞的作用力下，换向结构疲劳寿命是影响整个摇臂式喷头使用寿命的关键因素。影响碰撞力大小的因素主要有弹簧刚度、导流器17水平方向受力大小及杆4、6、7的长度等。因而，对碰撞力的大小进行优化，使其在一定工况下的碰撞力最小，同时又能够顺利换向。如表3所示，将弹簧刚度K、杆长l3、l4、l5作为设计变量，其初始值以及变量变化范围根据实际情况初步制定于表中。

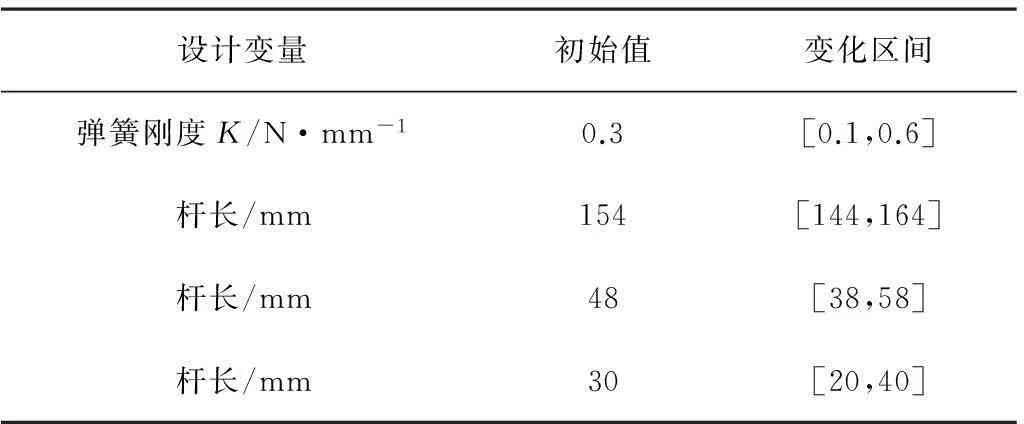
表3　设计变量表

4.2　优化分析

设定目标函数为求转动杆和挡板之间的换向碰撞力的最大值为最小，对各设计变量设置4个水平的分段点，进行优化设计研究。5次主要的碰撞受力优化迭代，如图7所示。

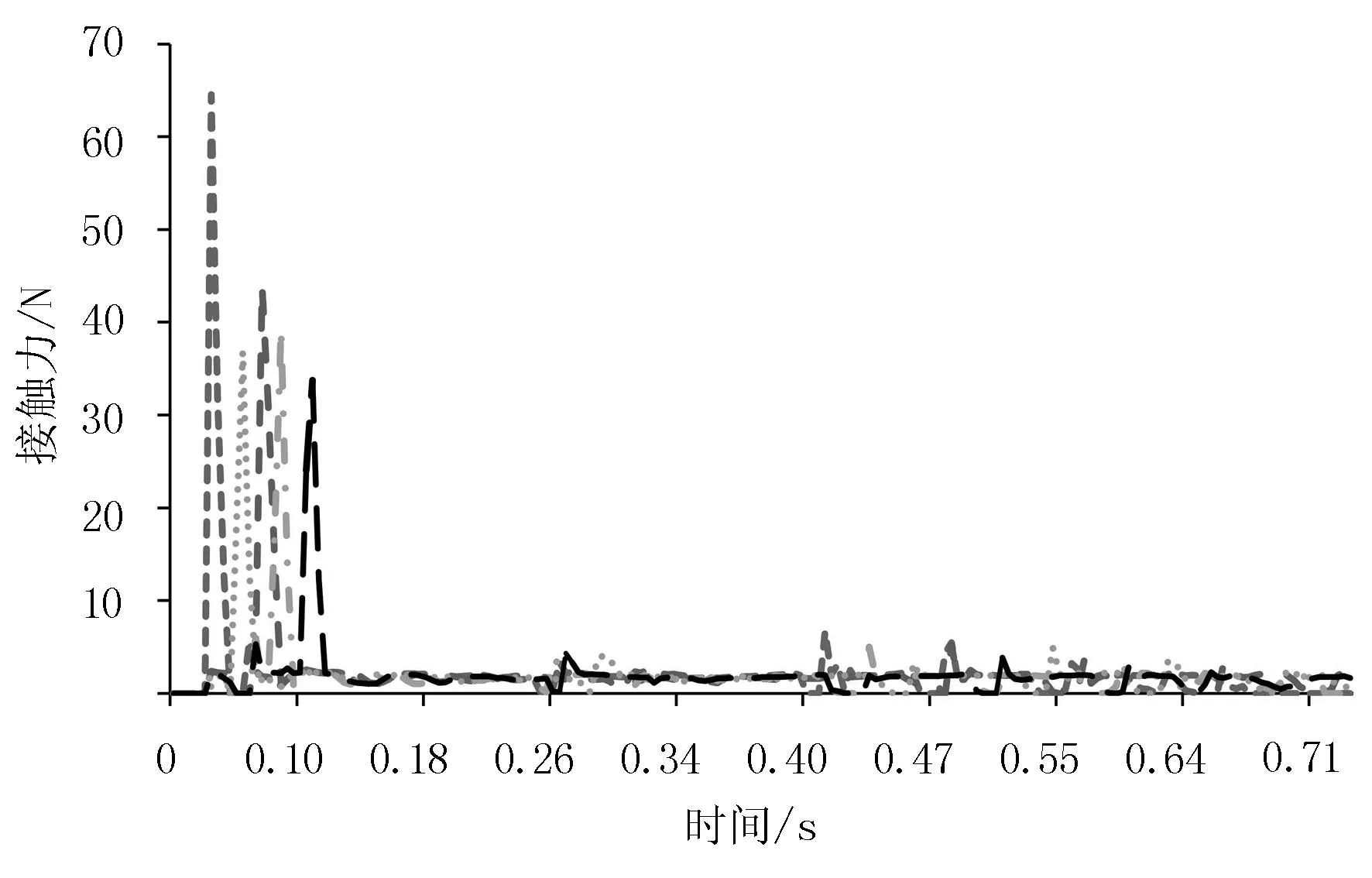
图7　碰撞力优化仿真图

优化后的碰撞力最大值变为33.75N，降低了55.9%；优化后的弹簧刚度为0.36，l3=150.2mm，l4=53.6mm，l5=33.5mm；优化取得了显著的效果。

5结论

1)构建了垂直摇臂式喷头的原理简化图，利用虚拟样机软件对其进行了参数化建模，得到了其动力学仿真模型。综合考虑了摇臂与转轴、喷管与水管密封等部位实际的摩擦，并通过试验数据进行了校验，得到了与真实受力运动状态下喷头特性符合较好的运动学和动力学参数。弥补了现有有限元分析等方法对实际的情况过于简化的不足。搭建的虚拟样机模型可以为今后静力分析，动力学疲劳等分析提供数据基础。

2)采用ADAMS参数化与三维软件混合建模的方式，基于构建的参数点，设置了弹簧刚度、影响换向顺利程度的杆长等参数为设计变量。对喷头换向机构的碰撞特性进行了优化，优化后的换向杆碰撞力减小了近55.9%，对改善喷头的动力学特性进行了初步探索。优化取得了显著的效果。

参考文献：

[1]袁寿其,李红,王新坤,等.中国节水灌溉装备发展现状、问题、趋势与建议[J].排灌机械工程学报,2015,33(1):78-92.

[2]李世英．喷灌喷头理论与设计[M]． 北京:兵器工业出版社，1995．

[3]列别捷夫．喷灌机械理论和构造[M].北京：中国机械出版社，1981.

[4]陈雷．垂直摇臂式喷头运动原理的研究[D]．北京: 华北水利水电学院北京研究生部，1985．

[5]王祺铭，严海军，剧锦三，等．PY140 型摇臂式喷头摇臂碰撞过程数值模拟[J]． 农业机械学报，2010，41(1) :86-91．

[6]李红，刘振超，汤攀，等．SR100 垂直摇臂式喷头摇臂有限元分析[J]． 排灌机械工程学报，2014，32(5) : 429-434．

[7]汤攀，李红，陈超，等.考虑配重的垂直摇臂式喷头摇臂运动规律及水力性能[J].农业工程学报，2015，31(2)：37-44.

[8]汤攀，李红，陈超，等． 垂直摇臂式喷头导流器的流固耦合分析[J]． 排灌机械工程学报，2015，33(3) :267-272．

[10]Li Hong, Yuan Shouqi, Xiang Qingjiang, et al. Theoretical and experimental study on water offset flow in fluidic component of fluidic sprinklers [J].Journal of Irrigation and Drainage Engineering, 2011, 137(4): 234-243.

[11]Yan Haijun, Ou Yangjun, Kazuhiro Nakano, et al. Numerical and experimental investigations on internal flow characteristic in the impact sprinkler [J].Irrigation and Drainage systems, 2009, 23(1): 11-23.

[12]李增刚. ADAMS入门详解与实例[M].北京:国防工业出版社,2007.

Dynamic Simulation and Optimization of Vertical Impact Drive Sprinkler by Considering Friction Coefficient

Tang Yue，Zhao Jin，Chen Chao

(Research Center of Fluid Machinery Engineering and Technology, Jiangsu University, Jiangsu 212013, China)

Abstract：As to the problems of over-simplification to the friction coefficient and impact between parts of vertical impact drive sprinkler. Taking Nelson SR100 vertical impact drive sprinkler as research object, the actual friction conditions between swing arm and spindle or effuse and pipe seal were comprehensively considered. A dynamics simulation model of vertical impact drive sprinkler was established based on virtual prototype software ADAMS. The coefficient of friction between different parts is defined by the test data acquired. The horizontal and vertical force simulation functions of deflector were constructed by STEP function in a complete cycle including free and non-free moving period. Two major actions: vertical hunting and horizontal stepping of the sprinkler were simulated. The last reversing simulation was conducted to test the magnitude of impact force. Taking the magnitude of impact force as target function and the reverse rod length or other factors as constraints, the magnitude of impact force was optimized based on the parametric modeling and optimization function of the software. The maximum of impact force optimized was reduced by 55.9%. The results of the optimization can be used to analyze the structural strength or the fatigue life of the sprinkler.

Key words：vertical impact drive sprinkler； friction coefficient； dynamics simulation； parametric modeling； impact force optimization

中图分类号：S277.9+4

文献标识码：A

文章编号：1003-188X(2016)09-0028-05

作者简介：汤跃(1955-)，男，江苏镇江人，研究员，(E-mail)tomt@ujs.edu.cn。

基金项目：江苏省基础研究计划青年基金项目(BK20140565)；江苏省农业科技支撑计划项目(BE2012385)

收稿日期：2015-08-25