基于MATLAB函数的节理网络模拟及其应用研究

闫 骁，侯明勋，李春光((.上海交通大学船舶海洋与建筑工程学院，上海 0040；.中国科学院武汉岩土力学研究所，武汉 43007))

岩体变形和强度数值模拟研究是岩体力学与工程领域里十分重要的研究课题之一。处于地壳表层的岩体由于受到地应力、温度变化、长期风化和剥蚀作用、构造运动等多种地质因素的影响，其内部会形成各种不同规模和数量的不连续面。岩体除了受到较大尺寸的断层或层理切割外，更多地是受到尺寸较小的随机节理的切割，从而使岩体中形成了随机节理网络体系[1]。所谓节理是对岩体中发育最为广泛的一类沿断裂面没有位移或仅有微量位移的断裂的统称[2]，它们往往对岩体的变形和破坏起着控制作用。对于节理岩体力学性质的研究，由于节理分布的随机性问题往往很难定量求解，即使采用大尺寸的现场岩体力学试验也很难获得具有代表性的岩体力学性质参数。从20世纪70年代以后，开始出现岩体节理网络计算机模拟技术[3]，从系统地研究节理参数的统计分析方法开始[4-7]，逐步发展到节理网络模拟技术[8,9]。由于采用计算机技术重现岩体力学中节理、裂隙等软弱结构面扩展破裂的力学过程具有直观、简明等特点，目前利用数值模拟方法来分析节理岩体的力学特性已成为研究岩体变形和强度性质的重要手段。

天然岩体中的随机节理网络计算机模拟主要是根据节理的走向、倾角和迹长等几何参数的宏观统计规律[8]，基于Monte Carlo方法自动生成随机节理网络模型[10]，然后在节理网络上进行有限元网格剖分[11,12]，并进一步通过建立适当的数值模型来计算岩体力学参数[13,14]。针对节理岩体的数值模拟方法，对于含有较少节理的岩体主要采用节理单元法[15]，而对于含有节理数量众多的岩体则主要采用等效连续模型[16]、离散元法[17]、非连续变形分析法[10]等，为节理岩体的力学分析提供了十分有效的工具。

本文基于MATLAB函数编制了节理网络模拟程序，并运用distmesh2d程序[18,19]实现了节理网络上的有限元网格自动剖分，最后通过算例分析了节理岩体力学参数的尺寸效应，验证了程序的可行性和有效性，为进一步研究节理岩体的变形和强度特性以及本构关系提供了基础。

1 基于MATLAB函数的随机节理网络自动生成

1.1 岩体二维随机节理网络生成方法

大量现场数据的统计结果表明，随机分布的节理是可以用某种概率统计规律表示的。在已知随机节理几何参数的统计规律后，可以根据其概率分布函数建立节理的数学模型，用Monte Carlo法生产一系列代替倾角、迹长、间距、倾向等节理几何参数的随机数，从而利用计算机模拟技术来生成节理岩体的随机网络图。二维节理岩体网络主要生成步骤可以概括为[10,13]：

(1)在选取的计算区域内，估算该区域内每组节理的条数N：

N=S/(dl)

(1)

式中：S为计算区域的面积；d为节理间距的平均值；l为节理迹长的平均值。

(2)根据节理中心点的分布规律，利用随机数生成函数得到N条节理的中心点坐标；然后再由节理方位和迹长参数确定相应节理的终点坐标。

(3)根据N条节理的起点和终点坐标，得到N条随机节理。

(4)检查每条节理是否超出了计算区域的边界，利用布尔运算截掉超出计算区域边界的部分，并更新节理的起点和终点坐标。

(5)利用布尔运算把区域外的随机节理除去。

(6)对每组节理重复步骤(1)～(5)。

1.2 随机节理网络模拟的MATLAB实现方法

基于1.1节给出的随机节理网络生成方法，利用MATLAB函数实现的具体过程可以简要描述为：

(1)首先确定计算域内的节理组数M。

(2)根据每组节理的几何参数统计分布规律，按式(1)确定计算域内各组节理的条数N，利用随机函数random( )[20]分别生成各组节理的中心点、方向角和迹长。

(3)根据几何关系确定所有节理的起点和终点坐标，并将其存放入节理数组Joins( )。

(4)自定义函数Isintersect( )判断计算域中的节理是否相交。若节理相交，则将两相交节理在交点处断开并生成新的节理，如图1所示，节理①、②和③为按照节理几何参数统计规律自动生成的节理，而1～7为相交节理进行处理后重新编号的节理。循环计算域内所有节理，重新获得计算域内的所有节理集合。

(5)用函数plot2d[20]绘制计算域内的节理网络图。

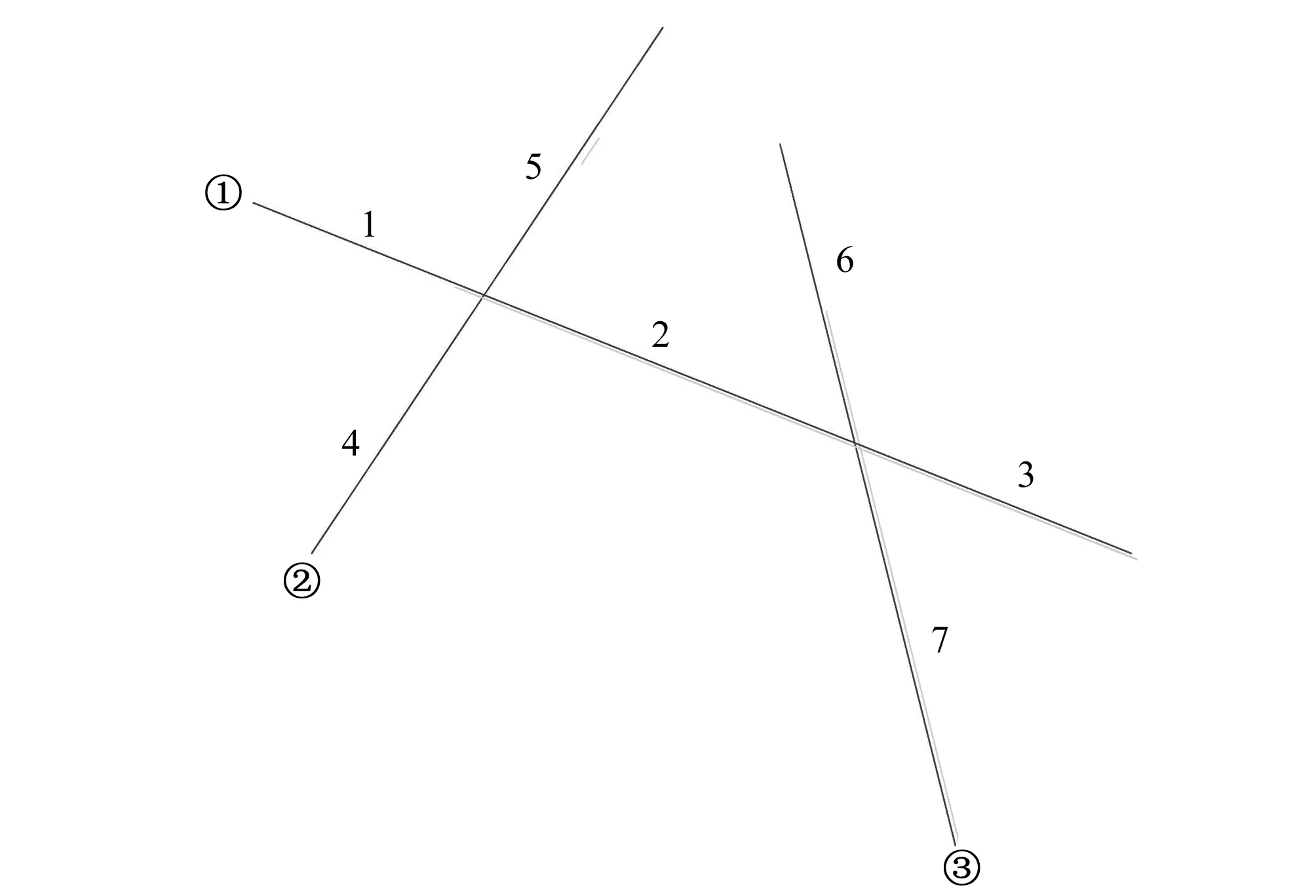
图1 相交节理示意图Fig.1 Sketch of intersected joints 注：戴圈数字代表原节理号；数字代表相交处理后的节理号。

1.3 节理网络有限元网格自动剖分

采用有限元法研究节理岩体的变形和强度特征时，就必需在已生成的随机节理网络图上进行有限元网格剖分。一般来说，当计算分析域内的节理数量较少时，往往可以采用人工方法处理岩体中的节理单元。但当计算域内的节理数目较多时，再由人工方法来准备数据就显得费事、效率低下，这种情况下如能借助于自动网格生成器就会大大提高计算效率。目前有限元网格自动生成方法有很多，其中应用比较广泛的方法是行波法(Advancing Front Method)和Delaunay三角分解法(Delaunay Triangulation)[11-13, 21,22]。为了采用有限元方法分析节理岩体的力学性质，在1.2节自动生成随机节理网络图的基础上，尝试采用distmesh2d[18,19]程序来实现节理网络图上的有限元网格自动生成。

首先，基于1.2节生成的计算域内的节理网络图，根据预先设置的单元网格尺寸，利用MATLAB中的linspace函数将节理和边界离散成散点数据；然后运用unique函数判断计算域内代表节理的所有线段的端点、离散点是否有重复，若有，则进行删除；最后由distmesh2d函数对计算域进行有限元网格剖分。该函数的调用格式为：function [p, t]=distmesh2d(fd,fh,h0,bbox,pfix,varargin)，其中，输出参数p为网格点坐标，t为输出网格任意三角形的3个顶点。输入参数的具体说明可参见文献[18]。

1.4 随机节理网络模拟实例

基于上述随机节理网络模拟过程，编制了MATLAB程序。图2给出了节理网络生成及有限元网格自动剖分的程序流程图。为了检验节理网络的实际模拟效果，本文分别选取1组节理和2组节理进行了节理网络模拟，节理几何参数如表1所示[10]，生成的节理网络如图3所示，相应的有限元网格如图4所示，算例的模型尺寸为14 m×14 m。

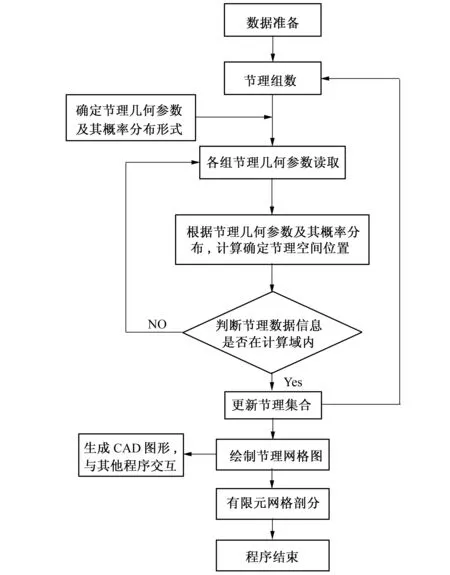
图2 节理网络模拟及有限元网格剖分流程图Fig.2 Flowchart of Random joint network simulation and FEM mesh generation

图3 随机节理网络图Fig.3 Random joint network

图4 随机节理岩体有限元网格图Fig.4 FEM mesh for random jointed rock mass

2 节理岩体力学参数REV估算

节理岩体的变形和强度参数往往会受到节理分布特征的影响，由于在实际工程中也很难直接通过物理试验方法获得节理岩体力学参数，目前采用数值分析方法来研究节理岩体的力学特性已成为一种行之有效的手段之一。这里根据给出的节理几何参数和网格剖分方法建立了某节理岩体的有限元数值分析模型，详细研究了节理岩体弹性模量尺寸效应问题。根据表2中给出的节理几何参数，建立了模型尺寸从2 m×2 m到14 m×14 m变化的节理网络图，共计有7组数值试验的试件。为使计算结果具有一定的代表性，每组数值试件至少选取12个样本进行计算。计算时所选取的完整岩石和节理的力学性质参数如表2所示。图5和图6分别给出了含有1组节理的数值试件在单轴加载条件下获得的应力应变曲线。对比图5和图6不难看出，随着模型尺寸的增大，应力应变曲线逐渐由相对分散趋于一致，这与文献[23]的结果相吻合。

根据有限元计算获得的数值试件的应力～应变曲线特征，通过线性拟合方法计算了不同尺寸条件下的弹性模量值。图7给出了分别含有1组节理和2组节理情况下的弹性模量随模型尺寸的变化关系。从图7中可以看出，含单组节理的情况下，弹性模量REV接近14 m×14 m，约为平均迹长的2.4倍，这与REV为典型节理迹长的3倍的结论接近[13, 24]；含2组节理的情况下，从图7不难看出其弹性模量REV要大于含单组节理的情况。

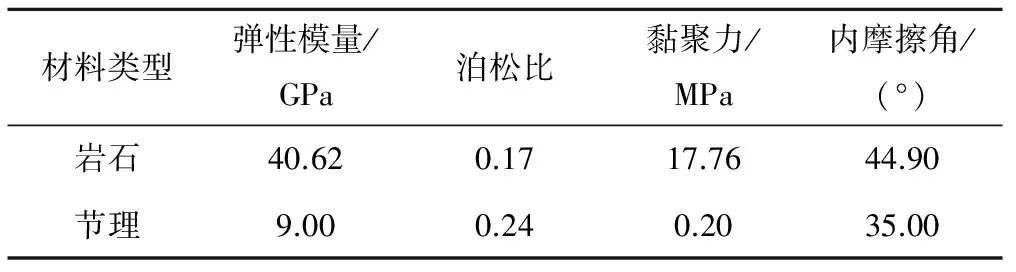
表2 岩石和节理材料参数Tab.2 The parameters of rock and joints

图5 节理岩体模型尺寸为4 m×4 m的应力应变曲线Fig.5 Curve of stresses vs. strains for jointed rock mass with size of 4 m×4 m

图6 节理岩体模型尺寸为14 m×14 m的应力应变曲线Fig.6 Curve of stresses vs. strains for jointed rock mass with size of 14 m×14 m

图7 岩体弹性模量随尺寸的变化曲线Fig.7 Curve of elastic modulus vs. model size for jointed rock mass

3 结 语

本文根据随机节理的分布特征，采用MATLAB函数实现了随机节理网络模拟，编制了相应的计算机程序。同时，结合distmesh2d函数在节理网络图上实现了有限元网格自动剖分，为采用有限元方法分析节理岩体的力学性质参数奠定了基础。按照节理概率分布形式，通过选取弹塑性有限元分析模型，获得了节理岩体不同尺寸上的弹性模量值，据此估算了节理岩体弹性模量REV。本文的工作是初步的，关于岩体力学参数，特别是强度参数与尺度之间的关系还有待进一步深入分析和研究。

□

[1] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002.

[2] 王 宏, 陶振宇. 边坡稳定分析的节理网络模拟原理及工程应用[J]. 水利学报, 1993,(10):20-27.

[3] 陶振宇, 王 宏. 岩体节理网络模拟技术研究[J]. 长江科学院院报, 1990,(4):18-26.

[4] Priest S D, Hudson J A. Estimation of discontinuity spacing trace length using scanline[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1981,19(2):183-197.

[5] Hudson J A, Priest S D. Discontinuity frequency in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1983,20(1):73-89.

[6] Einstein H H, Veneziano D, Baecher G B, et al. The effect of discontinuity persistence on rock slope stability[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1983,20(5):227-236.

[7] Sen Z, Kazi A. Discontinuity spacing and RQD estimates from finite length scanlines[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984,21(4):203-212.

[8] 徐光黎, 潘别桐, 唐辉明，等. 体结构模型与应用[M]. 武汉: 中国地质大学出版社, 1993.

[9] 陈剑平, 肖树芳, 王 清. 随机不连续面三维网络计算机模拟原理[M]. 长春: 东北师范大学出版社, 1995.

[10] 焦玉勇, 张秀丽, 李廷春. 模拟节理岩体破坏全过程的DDARF方法[M]. 北京: 科学出版社, 2010.

[11] 庞作会, 邓建辉, 葛修润. 在节理网络图上全自动生成有限元网格[J]. 岩石力学与工程学报, 1999,18(2):197-200.

[12] 朱冬林, 向 彤, 葛修润. 基于约束Delaunay三角划分法在节理图上实现网格自动剖分[J]. 岩石力学与工程学报, 2004,23(11):1 841-1 846.

[13] 庞作会.基于节理网络模型的岩体REV数值估算与无网格伽辽金法(EFGM)[D]. 武汉: 中国科学院武汉岩土力学研究所, 1998.

[14] Jian-Ping Yang, Wei-Zhong Chen, Yong-hao Dai, et al. Numerical determination of elastic compliance tensor of fractured rock masses by finite element modeling[J]. International Journal of Rock Mechanics & Mining Sciences, 2014,70:474-482.

[15] Goodman R E, Taylor R L, Brekke T L. A model for the mechanics of jointed rock[J]. Journal of the Soil Mechanics and Foundations Division, 1968,94(3):637-660.

[16] 朱维申, 王 平. 节理岩体的等效连续模型与工程应用[J]. 岩土工程学报, 1992,14(2):1-11.

[17] 贾 超, 王志鹏, 朱维申. 节理网络模拟的程序实现及其在地下洞室中的动态响应分析[J]. 岩土力学, 2011,32(9):2 867-2 872, 2 879.

[18] Persson P O, Strang G. A Simple Mesh Generator in MATLAB[J]. SIAM Review, 2004,46(2):329-345.

[19] Persson P O. Mesh generation for implicit geometries[D]. Massachusetts: Massachusetts Institute of Technology(MIT), 2004.

[20] 丁 伟. 精通MATLAB R2014a[M]. 北京: 清华大学出版社, 2015.

[21] Sullivan J M, Charron G, Paulsen K D. A three-dimensional mesh generator for arbitrary multiple material domains[J]. Finite Element in Analysis and Design, 1997,25(3-4):219-241

[22] Gdias N A, Dutton R W. Delaunay triangulation and 3D adaptive mesh generation[J]. Finite Element in Analysis and Design, 1997,25(3-4):331-341.

[23] 张红亮. 节理岩体变形与强度的尺度效应及REV问题研究[D]. 武汉:中国科学院武汉岩土力学研究所, 2007.

[24] Masanobu O. An equivalent continuum model for coupled stress and fluid flow analysis in jointed rock masses[J]. 1986,22(13):1 845-1 856.