东江干流与支流河涌洪水遭遇风险研究
2016-03-23黄锋华黄本胜广东省水利水电科学研究院广州510610广东省水动力学应用研究重点实验室广州510610河口水利技术国家地方联合工程实验室广州510610
黄锋华, 黄本胜,郭 磊,谭 超,胡 培(1.广东省水利水电科学研究院,广州 510610;2.广东省水动力学应用研究重点实验室,广州 510610;3.河口水利技术国家地方联合工程实验室,广州 510610)
对于某一特定流域来说,流域防洪排涝设计不仅与流域集雨范围内降雨形成洪水有关,还与外江洪水相遭遇的外江洪水位息息相关;也就是说,某一流域设计洪水和与之相组合的外江设计洪水(流量或水位)是分析该流域排涝方案和排涝设施规模的依据。因此,为合理确定流域防洪排涝设计规模,必须知道流域暴雨洪水与外江洪水遭遇的概率风险规律,从而选定的流域设计洪水与外江洪水组合对防洪排涝计算才真正的具有重现期意义。
对于洪水的遭遇分析,常用的方法是根据研究区域历年同步洪水资料进行水文学分析法或简单统计[1-3],这些方法只能对已发生的洪水进行简单的统计,对于洪水发生概率分布、洪水遭遇重现期的风险内容难以做到定量分析计算。近年,多变量联合分布在多变量极端洪水要素(洪峰、洪量、峰现时间)统计分析中成为研究热点,郭生练[4,5]等总结了Copula函数在水文分析计算的应用和研究进展,提出了Archimedean Copula 函数中几种常用于水文分析计算的函数及其适用性,其中Frank Copula函数能够描述正/负相关的随机变量,且对相关性的程度没有限制,适用性广。Copula函数因其结构简单、拟合效果优良等特点在多变量水文分析计算中得到了广泛的应用[6-9],刘曾美等[10-12]将Copula函数成功应用于洪水遭遇分析中。考虑到望江沥作为无资料小流域地区,洪水历时一般在1天内且降雨与洪水是同频的,本文采用望江沥(惠阳站为代表站)年最大24 h降雨作为年最大洪水作为望江沥暴雨洪水计算依据,采用Von Mises分布拟合博罗站年最大洪水和惠阳站年最大24 h降雨出现时间分布规律,通过Copula函数构建东江干流与支流望江沥年最大洪水发生时间及其量级联合分布,探讨东江干支流洪水遭遇风险特征,为望江沥流域防洪排涝设计和风险管理提供的理论支撑。
1 研究区域概况
东江是珠江流域在广东境内的三大水系之一,干流全长562 km,流域总面积35 340 km2,其中广东省境内31 840 km2;博罗水文站是国家基本水文站、东江流域下游干流关键控制站,控制流域面积25 325 km2,占全流域面积的72%,是东江干流汇入珠江三角洲河网的控制性站点,是东江流域的代表性水文站。惠阳站是东江流域重要水位雨量站,其位于望江沥河涌汇入东江干流交汇口的下游3 km(见图1),可作为望江沥流域(集雨面积不足20 km2的小流域)代表性雨量站。望江沥位于东江下游广东惠州市惠城区惠州大堤(北堤)的保护范围内,为东江河谷平原区,集雨面积为17.12 km2,河道平面干流河长8.3 km。望江沥流域所在区域位于惠城区,是惠州市的政府所在地和中心区,是惠州乃至整个东江流域政治、经济、文化和交通的中心,素有“粤东重镇”、“岭南名郡”的美誉。近年来,随着望江沥其周边城市迅速发展,流域内人口密集、经济总量大,对流域内防洪排涝设计提出了更高的要求,特别是惠州市成为第二批全国水生态文明城市建设试点后,提出了以“河清、湖美、惠民城”为创建理念和目标,将重点完成惠州城区内望江沥等河涌综合整治工程,对河涌防洪排涝设计工作提出更为严格的要求。惠州市中心城区有大小河涌10余条,均汇入东江干流,根据惠州市水生态文明实施方案,惠州市每年启动1~2条河涌综合整治项目,河涌与东江干流洪水遭遇风险分析,可为河涌综合整治防洪排涝方案设计提供依据。
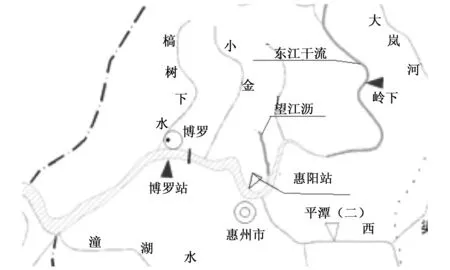
图1 东江干流、望江沥及相关站点位置示意图
2 研究方法
2.1 Copula函数
Sklar定理:设X、Y为连续的随机变量,其边缘分布函数分别为F(x)和F(y),F(x,y)为变量X和Y的联合分布函数,那么存在唯一的Copula函数C使得:
F(x,y)=P(X≤x,Y≤y)=Cθ[FX(x),FY(y)],∀x,y
(1)
式中:Cθ[FX(x),FY(y)]为Copula函数;θ为Copula 函数的参数。
在水文分析计算中最常用的几种函数有Gumbel Copula、Clayton Copula、AMH Copula和Frank Copula。本文选用适用性较强的Frank Copula进行量变量联合分布构建,其表达式如下:
(2)
式中:u、v均为单变量边缘分布;θ为Copula函数参数。
采用相关指标法[4]进行参数估计,即根据Kendall秩相关系数τ与参数θ之间的关系间接求出,表达式如下:
(3)
2.2 年最大洪水发生时间分布
方彬等[13]首次采用Von Mises分布拟合年最大洪水发生时间,研究表明Von Mises分布能较好地拟合年最大洪水发生时间。设洪水发生时间随机变量X服从Von Mises分布,则其密度函为:
(4)
0≤x≤2π, 0≤μ≤2π,k>0
式中:μ为位置参数(平均角);k为尺度参数;I0(k)为第一类0阶修正的Bessel函数。
对于双峰混合Von Mises分布则是由两个单一的Von Mises分布按一定比例p相加而得,其密度函数为:
f(x,μ1,μ2,k1,k2,p)=
p·f1(x,u1,k1)+(1-p)·f2(x,u2,k2)
(5)
式中:f1(x,u1,k1)、f2(x,u2,k2)表示两个单一的Von Mises分布;p表示两个单一Von Mises分布在混合分布中的比例。关于Von Mises分布函数参数可采用最小二乘法获取。
2.3 年最大洪水量级分布
根据《水利水电工程设计洪水计算规范(SL44-2006)》,采用皮尔逊Ⅲ型分布计算设计洪水,即年最大洪峰流量X和年最大24 h降雨Y服从皮尔逊Ⅲ型分布,其概率密度函数为:
(6)
α>0,β>0,δ≤y<+∞
式中:α、β和δ分别为皮尔逊Ⅲ型分布的形状、尺度和位置参数;Γ(*)为伽马函数。皮尔逊Ⅲ型分布参数估算可采用极大似然估计方法(MLE)[14]。
2.4 联合概率分布与重现期
根据Copula函数,两变量联合分布为:
F(x,y)=P(X≤x,Y≤y)=C[FX(x),FY(y)]
(7)
设FX(x)为博罗站年最大洪峰流量X边缘分布函数,FY(y)为惠阳站年最大24 h降雨量Y的分布函数。
则X和Y的联合重现期T0:
(8)
X和Y的同现重现期Tα:
(9)
边缘分布的重现期:
(10)
则有:
T0(x,y)≤min[T(x),T(y)]≤max[T(x),T(y)]≤Tα(x,y)
(11)
2.5 条件概率分布
F(x,y)=P(X≤x,Y≤y)的物理意义为博罗站年最大洪峰流量小于x, 同时惠阳站年最大24 h降雨量小于y的概率,其重现期为年。
给定X>x,Y的条件分布函数为:
(12)
给定Y>y,X的条件分布函数为:
(13)
3 东江干支流洪水遭遇风险分析
本文研究以1953-2013年(系列长度N1=61)博罗水文站年最大洪峰流量及其出现时间和惠阳站1974-2013年(系列长度N2=40)年最大24 h降雨及其出现时间序列为基础,假定年最大洪水均发生在汛期,并按广东汛期选取4月15日至10月15日(总天数L=184 d)的流量资料分别选取两站年最大洪水和年最大24 h降雨出现日期作为样本。本文所采用的水文气象数据来源于广东省水文局整编资料,数据可靠。
3.1 东江干支流洪水发生时间的遭遇分析
经样本分析,博罗站年最大洪水出现时间系列属于单峰过程,惠阳站年最大24 h降雨出现时间系列属于双峰过程。采用最小二乘法进行参数寻优,得到博罗站年最大洪水出现时间和惠阳站年最大24 h降雨出现时间Von Mises分布参数估算结果,两站拟合的均方根误差RMSE均较小,如表1所示。
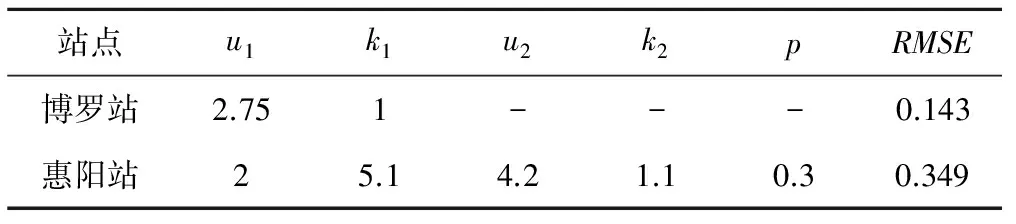
表1 Von Mises分布参数估算结果
以时间弧度(即4月15日对应弧度为0,10月15日对应弧度为2π)为横坐标,图2给出了博罗站年最大洪水出现时间概率密度分布fb和惠阳站年最大24 h降雨出现时间概率密度分布fh拟合情况,由图2可知,Von Mises分布能较好拟合博罗站和惠阳站极端水文事件出现时间分布。博罗站年最大洪水出现时间概率密度曲线为单峰过程,在7月4日出现概率最大,约为34.1%;惠阳站年最大24h降雨出现时间概率密度曲线为双峰过程,分别在6月14日和8月16日出现概率较大,分别为30.7%和25.2%。

图2 博罗站年最大洪水和惠阳站年最大24 h降雨出现时间概率密度拟合图
根据博罗站和惠阳站同步观测数据分析,fb和fh两同步序列Kendall系数 为0.112,呈现弱的正相关。根据Copula函数选取原则,选取Frank Copula函数构建两站的极端水文事件出现时间联合分布,参数估算采取相关性指标法,Copula函数系数 为1.02,均方误差RMSE为0.189,采用Gringorten公式[15]计算联合观测值的经验频率,并将博罗站年最大洪峰流量出现时间X和惠阳站年最大24 h降雨Y的经验频率和理论频率P-P绘于图3,从图中可知散点均落在45°直线对角线附近,表明所选Frank Copula函数拟合效果较好。在5%的显著水平下,Frank Copula联合分布χ2=0.29<χ20.995(31)=15.46,通过了χ2检验。
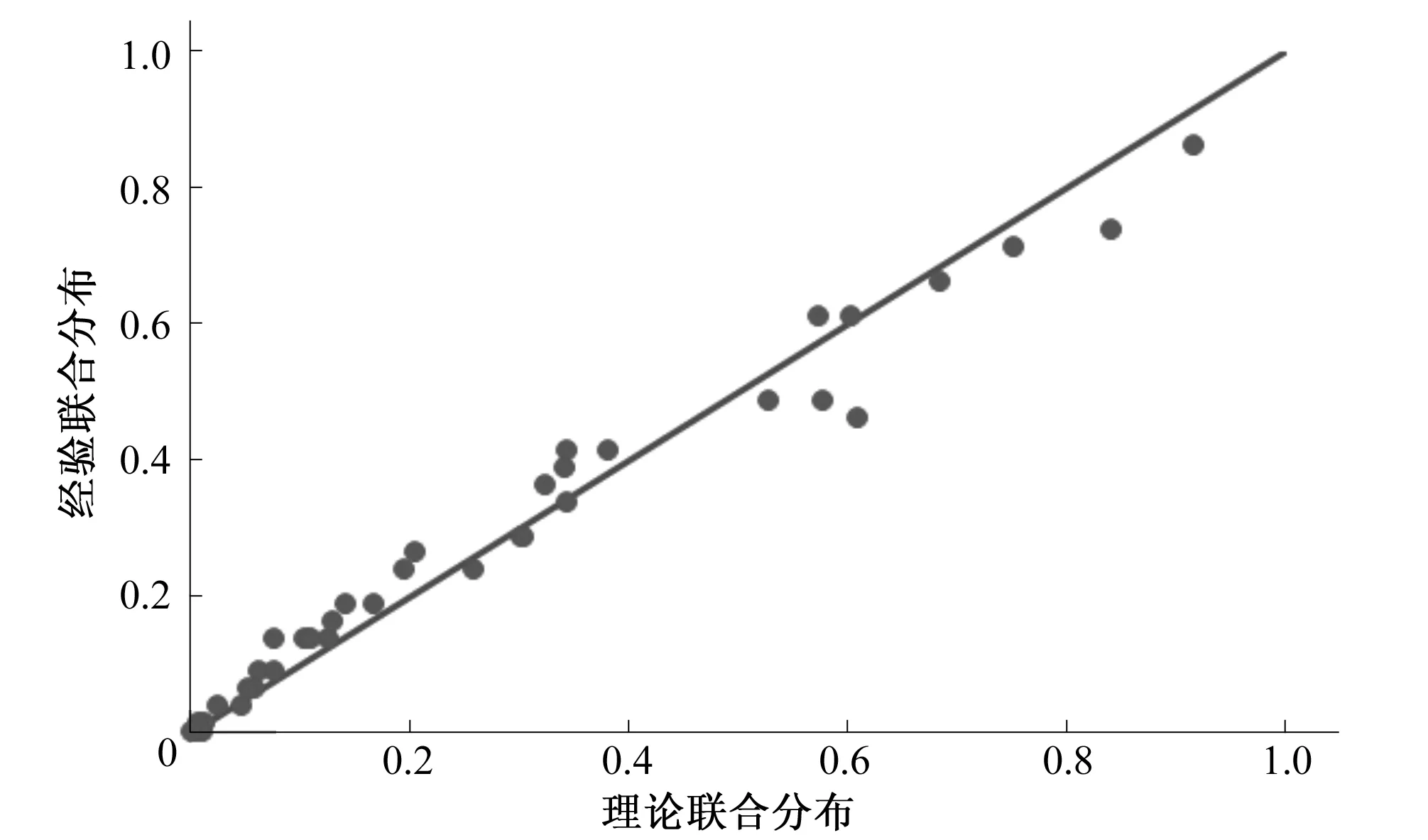
图3 年最大洪水和年最大24 h降雨出现时间经验值与理论值P-P图
根据Copula函数定义,望江沥洪峰与东江干流洪峰遭遇是指在不考虑洪峰量级情况下,两者洪峰在同一天出现,由此可以定义东江干流(博罗站)与望江沥年最大洪水发生时间在第i天遭遇的风险为:
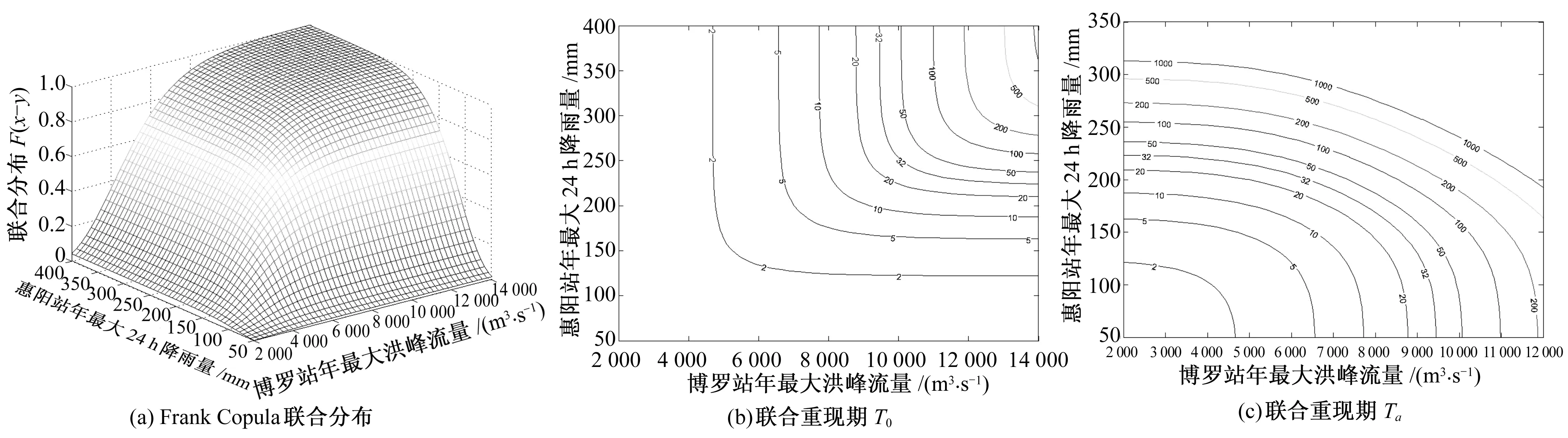
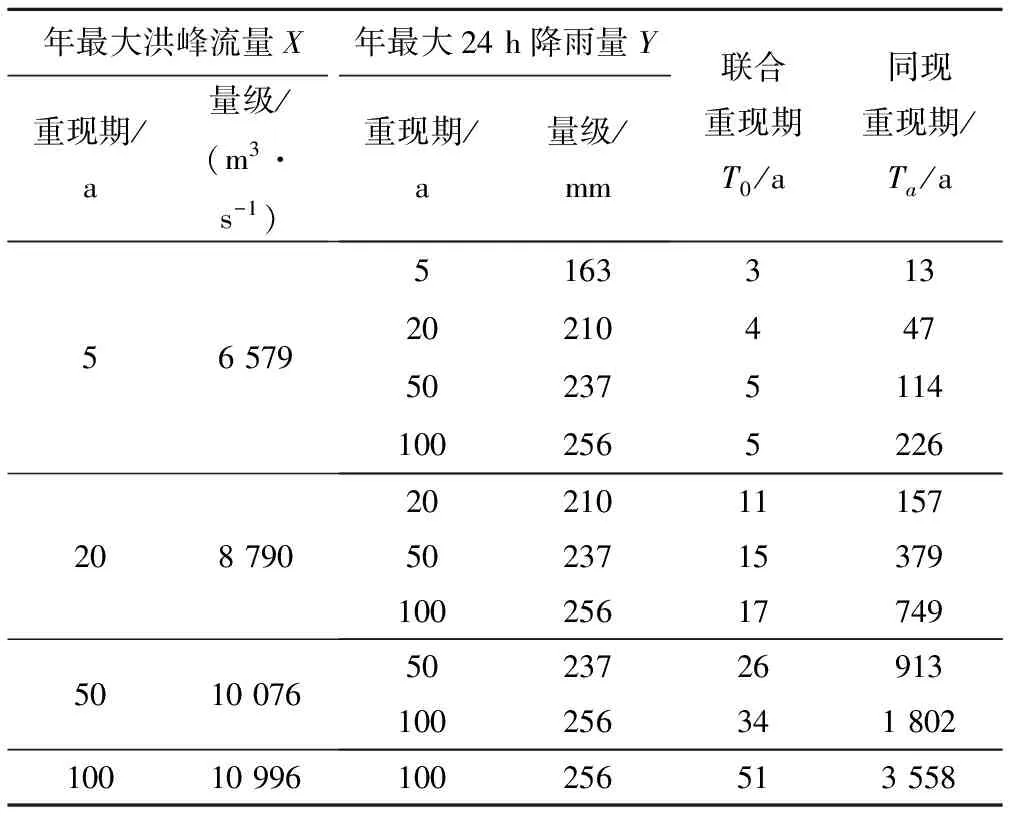
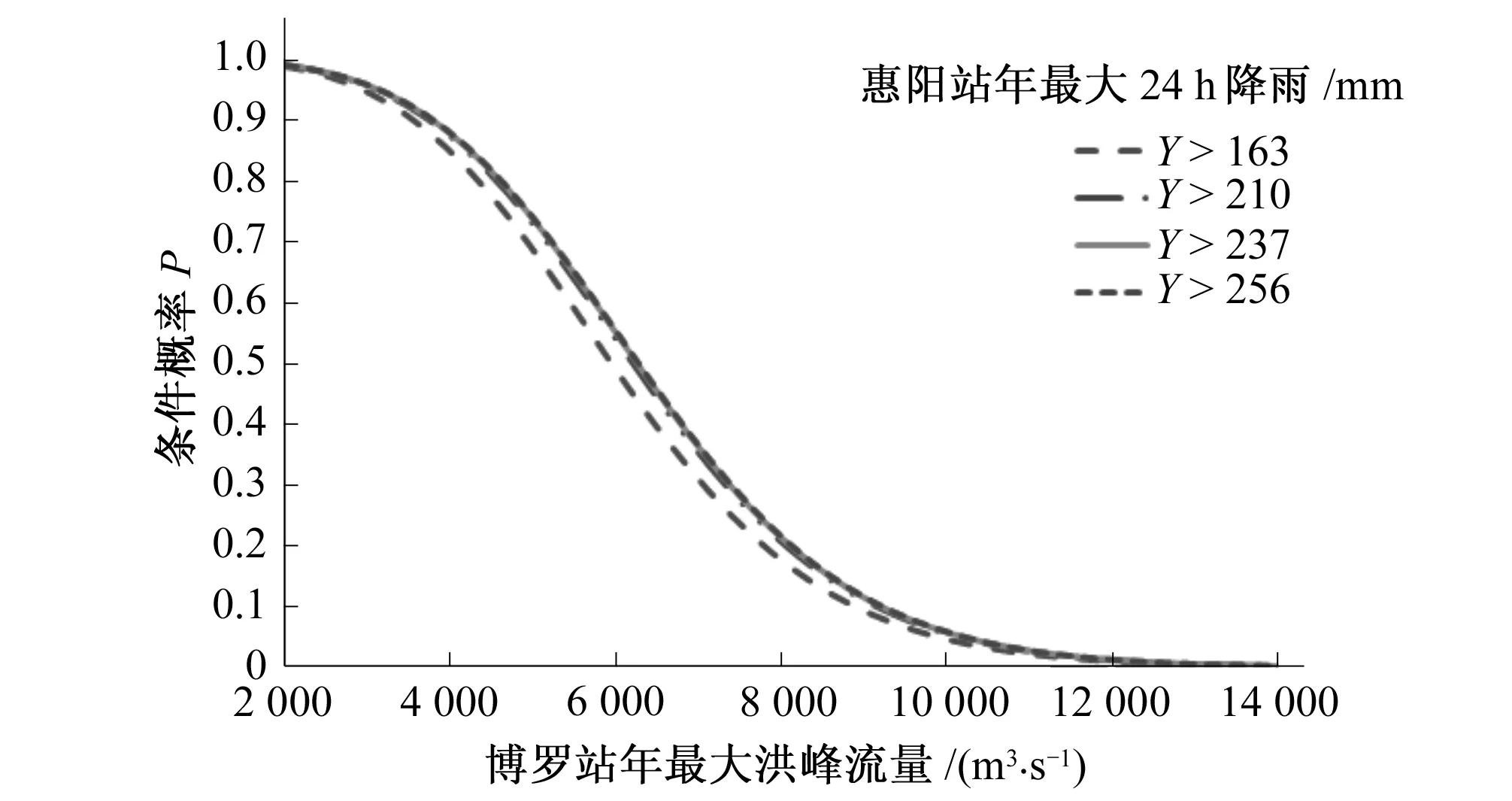
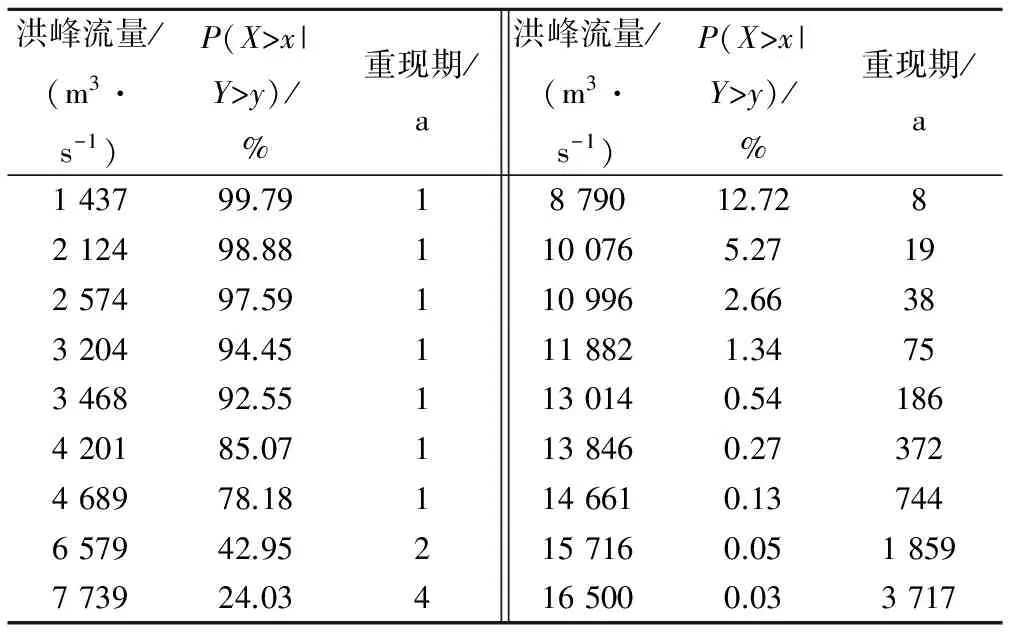
pi=P(ti≤X F(ti,ti)+F(ti+1,ti+1)-F(ti,ti+1)-F(ti+1,ti) (14) 式中:pi为东江干流(博罗站)与其支流望江沥年最大洪水发生时间在第i天遭遇的概率;F(ti,tj)为东江干流(博罗站)和其支流望江沥洪水分布发生在第i天和第j天前的联合概率。 图4给出了东江干流(博罗站)与其支流望江沥洪峰日遭遇的概率分布曲线。从图中可以看出,东江干流与其支流望江沥遭遇最大可能发生在6月17日,遭遇风险约为0.011%,6月2日至7月9日是东江干支流出现洪峰遭遇的集中时期,7月10日至8月10有一个相对平稳的遭遇风险,约为0.006%,东江干支流在5月9日之前和10月6日之后发生遭遇的概率很小,几乎为0。 图4 东江干流与其支流望江沥洪峰日遭遇的风险分布 博罗站年最大洪水和惠阳站年最大24 h降雨边缘分布及联合分布参数估算成果见表2,由表2可知,两站皮尔逊Ⅲ型曲线对经验样本拟合的均方根误差RMSE较小。统计表明,东江干流博罗站年最大洪峰流量和惠阳站年最大24 h降雨量成弱的正相关,Frank Copula函数构建了两者的联合概率分布,其参数θ依据Kendall系数求得为2.69,均方误差RMSE为0.296,在5%的显著水平下,Frank Copula联合分布χ2=0.28<χ20.995(32)=15.13,通过了χ2检验,其经验值和理论值的P-P图集中分布在45°直线对角线附近,为省去篇幅不再列出图。 表2 博罗站年最大洪水和惠阳站年最大24 h降雨边缘分布及联合分布参数估算表 根据Copula函数定义,东江博罗站出现年最大洪峰流量大于某一量级洪水,遭遇东江支流望江沥(惠阳站)发生年最大24 h降雨量大于某一量级暴雨的风险或重现期,可由式(9)表示。图5给出了博罗站年最大洪峰流量X和惠阳站年最大24 h降雨量Y联合分布三维图、联合重现期和同现重现期的等值线图,从图5中可以更加清楚地了解联合分布函数。从表3可知,东江干流(博罗站)发生年最大洪峰流量超过6 579 m3/s的重现期为5年,东江支流望江沥(惠阳站)发生年最大24 h降雨量超过210 mm的重现期为20年,则其联合重现期T0为4年,即东江干流博罗站发生超5年一遇洪水或者东江支流望江沥(惠阳站)发生超20年一遇暴雨洪水的重现期为4年;而东江支流望江沥(惠阳站)发生超20年一遇暴雨同时遭遇东江干流博罗站发生超5年一遇洪水的重现期为47年,即同现重现期Ta为47年。 图5 年最大洪水和年最大24 h降雨联合分布三维图、联合重现期和同现重现期等值线图 表3 博罗站年最大洪水和惠阳站年最大24 h降雨联合重现期和同现重现期 当东江支流望江沥(惠阳站)发生某一量级以上的暴雨洪水的条件下,东江干流(博罗站)的概率分布,对研究望江沥设计洪水与东江干流洪水遭遇具有重要意义。图6给出了东江干流(博罗站)发生特定量级以上洪水条件下,望江沥(惠阳站)发生某一量级以上暴雨洪水的概率分布曲线;图7给出了望江沥(惠阳站)发生特定量级以上暴雨洪水条件下,东江干流(博罗站)发生某一量级以上洪水的概率分布曲线。表4给出了望江沥(惠阳站)发生P=5%暴雨洪水条件下,东江干流(博罗站)年最大洪水洪峰量级的概率分布。例如,望江沥(惠阳站)发生20年一遇暴雨洪水的条件下,东江干流(博罗站)发生洪峰量级超过6 579 m3/s(5年一遇,见表3)洪水重现期为4年,发生洪峰量级超过10 996 m3/s(100年一遇,见表3)洪水重现期仅为38年;表明望江沥发生暴雨洪水的情况下,东江干流发生某一量级洪水的可能性提高。 图6 Y的条件频率P(X>y|X 图7 X的条件频率P(X>x|Y>y)曲线 表4 惠阳站发生大于P=5%暴雨条件下博罗站洪水量级概率分布 以东江下游博罗站年最大洪水和望江沥临近的惠阳站年最大24 h降雨资料为研究基础,采用Von Mises分布拟合暴雨洪水发生时间的概率分布,采用皮尔逊Ⅲ型分布拟合年最大洪水量级的概率分布,采用Frank Copula 函数构建了东江干流与支流望江沥洪水遭遇的联合分布,各分布函数的拟合效果较好,在0.5%显著水平下均通过了χ2检验。本文从暴雨洪水出现时间和量级分析了东江干流与支流望江沥联合概率分布特征以及遭遇分析分析,研究表明:东江干流(博罗站)和望江沥暴雨洪水出现时间和量级之间存在弱的正相关;东江干流(博罗站)与望江沥暴雨洪水在同一天遭遇最大可能发生在6月17日,遭遇风险约为0.011%,在5月9日之前和10月6日之后发生遭遇的可能性极小,几乎不会发生;望江沥发生超20年一遇暴雨同时遭遇东江干流超5年一遇洪水的重现期为47年;条件概率分布上看,在望江沥发生暴雨洪水条件下,东江干流(博罗站)某一量级的洪水发生的可能性相对提高。本研究较好地揭示了东江支流望江沥河涌与外江洪水遭遇的概率风险规律,可为望江沥河涌排涝布置方案和排涝设施规模设计提供参考。 □ [1] 肖天国. 金沙江、岷江洪水遭遇分析[J]. 人民长江,2001,32(1):30-32. [2] 李孝兵. 连江中上游干支流洪水遭遇问题分析[J]. 广东水利水电,2008,(5):42-48. [3] 戴明龙, 沈燕舟.长江上游与洞庭湖洪水遭遇规律研究[J]. 水资源与水工程学报,2010,21(6):117-120. [4] 郭生练,闫宝伟,肖 义,等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文,2008,28(3):1-7. [5] 闫宝伟,郭生练,郭 靖,等. 多变量水文分析计算方法的比较[J]. 武汉大学学报(工学版),2009,42(1):10-15. [6] 闫宝伟,郭生练,陈 璐,等.Copula函数在水文计算中的适用性分析[J]. 数学的实践与认识,2012,42(3):85-93. [7] 陆桂华,闫桂霞,吴志勇,等.基于Copula函数的区域干旱分析方法[J]..水科学进展,2010,21(2):188-93. [8] 陈子燊, 刘曾美,剑飞洪. 广东西江北江洪水联合概率分布研究[J].中山大学学报(自然科学版),2011,50(2):110-115. [9] 肖 义, 郭生练, 刘 攀,等. 基于两变量分布的峰量联合分析[J].长江科学院院报, 2007,24(2):13-16. [10] 刘曾美, 陈子燊. 区间暴雨和外江洪水位遭遇组合的风险[J].水科学进展,2009,20(5):619-625. [11] 闫宝伟, 郭生练,陈 璐,等. 长江和清江洪水遭遇风险分析[J].水利学报,2010,41(5):553-559. [12] 闫宝伟, 郭生练,余 维. 长江和清江洪水过程遭遇风险分析[J].水力发电学报,2013,32(1):50-53. [13] 方 彬,郭生练,肖 义,等.年最大洪水两变量联合分布研究[J].水科学进展,2008,19(4):505-511. [14] 程银才,范世香,李明华.一种新的水文频率计算方法[J].水文,2008,28(1):59-69. [15] GUO S L.A discussion on unbiased plotting positions for the general extreme value distributeon[J].Journal of Hydrology,1990,121(1-4):33-44.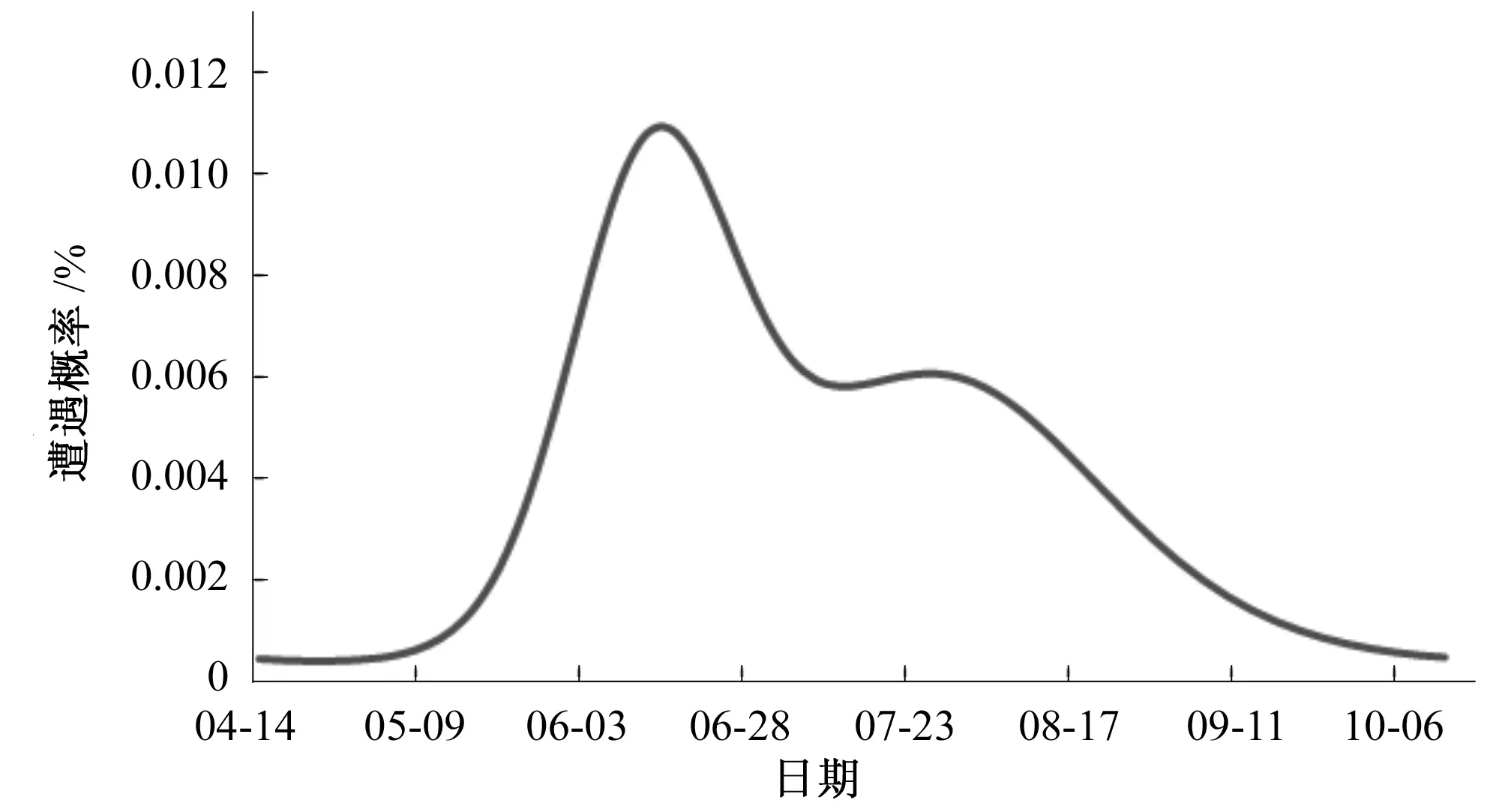
3.2 东江干支流洪水量级的遭遇分析

3.3 东江干支流洪水条件分布

4 结 论
