2种改进的TOPSIS模型在地下水水质评价中的应用研究

2016-03-23顾学志肖长来姜兴明梁秀娟王岳航

节水灌溉 2016年5期

顾学志，肖长来，姜兴明，梁秀娟，王岳航，娄洋

(1.吉林大学环境与资源学院，长春 130021；2.吉林大学地下水资源与环境教育部重点实验室，长春 130021)

地下水水环境质量评价是随着社会经济发展所造成的地下水环境问题日益突出而产生和发展起来的。目前，地下水资源问题在很大程度上是水质问题，尤其是各种人类活动改变了地下水水环境状态，使地下水资源因为水质变化而难以利用，从而严重制约了社会经济的发展[1]。地下水质量评价以地下水水质调查分析资料或水质监测资料为基础，虽然地下水水质评价方法有很多，如内梅罗指数法、聚类分析法、模糊数学法等，但这些方法模型往往存在局限性，如评价方法中涉及评价因子的选取，一般采取专家评判法，容易发生重点不突出等问题。灰色聚类法及模糊评判法，需要构造函数，存在一定的人为性，并且由于计算时丢失信息而导致评价结果与实际不符[2]。为了对水质进行更好的评价，笔者采用2种改进的TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)模型及采用熵权法确定客观因子权重，采用层次分析法确定主观因子的权重对吉林市进行地下水水质评价，以期达到更好的评价效果。

1 数据来源

采用在吉林市平原区8眼监测井2006年的水质监测数据，通过对水质数据的阴阳离子进行平衡分析，被选取数据的准确性得到很好的验证。以《地下水质量标准》(GB/T 14848-93)[3]为水质标准，选取总硬度、总锰、总铁、硝酸根、亚硝酸跟、硫酸根、及氟化物7项实测水质指标作为水质影响因子，对8眼监测井的水质进行评价。

2 研究方法

2.1 传统的TOPSIS方法

TOPSIS是理想值逼近排序法，是一种适用于以多属性指标为依据，对多个评价对象进行比较、排序的分析方法。通过构造了n维属性向量空间，确定正、负理想解，并求解各评价对象与正、负理想解之间的欧式距离，测度该评价对象在靠近正理想解的同时远离负理想解的叠加状态，并将此叠加状态作为衡量评价对象的综合指标[4]。但传统的TOPSIS法有一定的局限性，当2个评价对象位于正、负理想解之间的中垂线上时，对于正理想解的欧式距离可能与对于负理想解的欧式距离相等[5]，因此可能无法合理比较出这2个评价对象的优劣程度。

2.2 改进的TOPSIS方法

2.2.1基于“垂面距离”的TOPSIS方法----正交投影法[6-9]

以三维空间为例，3个坐标轴分别代表3个评价指标，A、B分别为评价方案中的正、负理想解。X、Y分别代表2个评价方案，这2个参评方案的垂面距离可概括为：以过正、负理想解A、B连线的直线为法向量，分别做经过X点与经过Y点的平面，如图1所示，即2个平面X1X2X3X4与Y1Y2Y3Y4，此2个平面之间的距离，也就是X、Y在直线AB上的正交投影点P和Q之间的欧氏距离。设A、B、X、Y所对应的向量分别为a、b、x、y，则X与Y的垂面距离为：

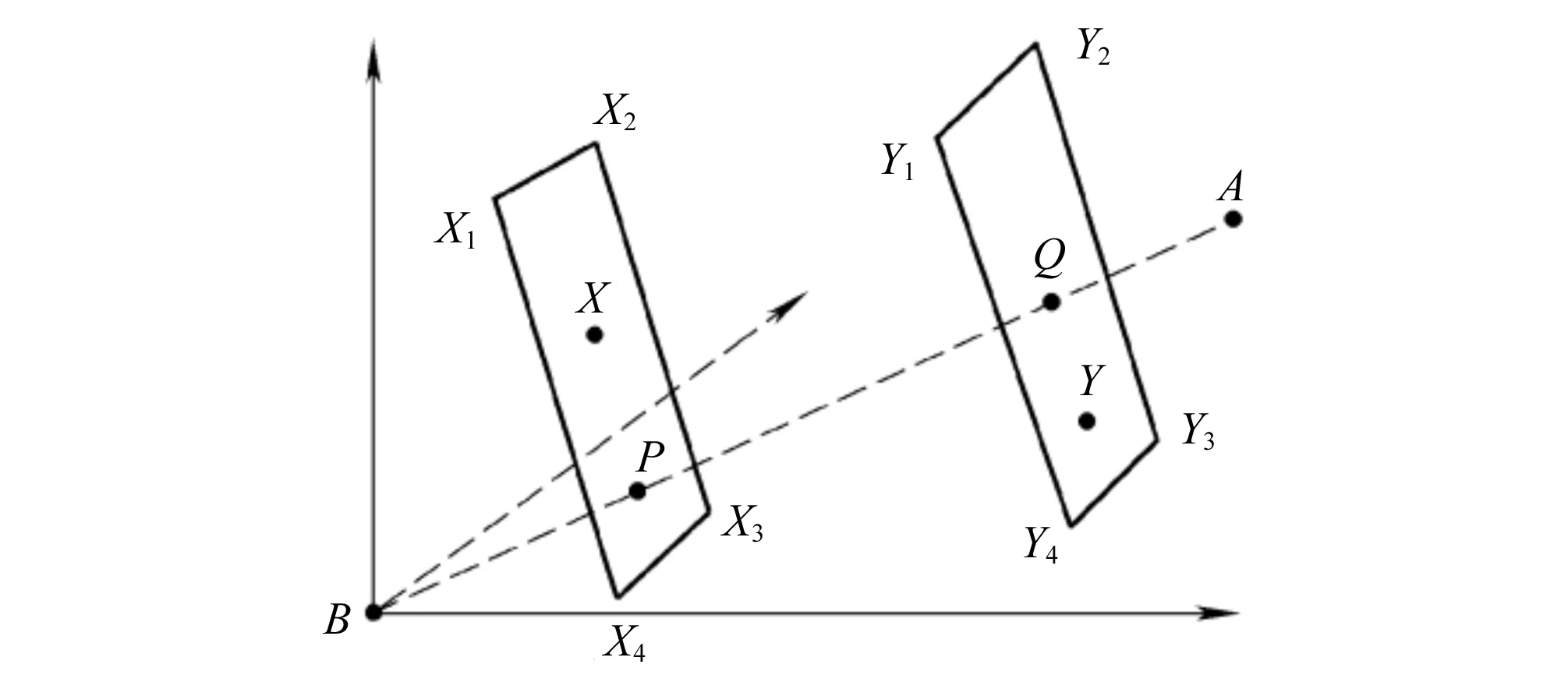
图1 垂面距离示意图Fig.1 Schematic diagram of vertical distance

正交投影法是以与理想解的“垂面距离”大小作为衡量评价指标优劣的标准，正交投影法在地下水水质评价中的具体计算步骤如下。

(1)建立评价集。设各水质监测点的集合为M=(M1，M2，…，Mm),评价指标集N=(N1，N2，…，Nn),Mi对指标Nj的值为aij，形成矩阵A=(aij)m×n：

(2)建立规范化矩阵以消除评价指标具有不同的量纲对评价结果产生影响，因此需要建立规范化矩阵，对各组评价方案进行无量纲化处理。即：

(1)

(3)将无量纲化矩阵与指标权重向量相乘，得到加权标准化矩阵R=(rij)m×n：

rij=wjviji=1,2,…,m;j=1,2,…,n

(2)

(4)确定计算正理想解和负理想解。j个指标的正理想解x+j及负理想解x-j,在地下水水质评价中：

(3)

(5)为了简化计算，将坐标原点平移到正理想点，平移后矩阵T=(tij)m×n：

tij=rij-x+ji=1,2,…,m;j=1,2,…,n

(4)

经过平移后，正理想解变为{0,0,…，0},负理想解变为：

(5)

(6)计算各待评价方案与理想解的“垂面距离”D。经过平移，此距离计算公式可简化为：

(6)

Di越小，水质等级越低，水质越好。

2.2.2基于Kullback-Leibler距离的TOPSIS方法----相对熵排序法[10]

文献[10]通过实例分析证明了基于Kullback-Leibler距离的相对熵排序法有效地解决了中垂线上点的排序问题，并且证明了此方法的正确性及稳定性。基于KL距离的TOPSIS法在地下水水质评价中的前4步与上述正交投影法的(1)、(2)、(3)、(4)相同，各监测点各个指标与正、负理想解之间的距离D+i、D-i采用KL距离来计算：

(7)

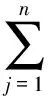
(8)

各监测点数值与理想解的相对贴进度:

(9)

根据Ci的大小对监测数据进行分级排序，Ci越大，水质越好。

3 权重的确定

权重的确定主要2种方法：一是主观赋权法，如层次分析法，此方法虽然能充分反映专家的知识和经验，因为将复杂的问题层次化，将定性问题定量化，所以评价结果有较强的主观性；二是客观赋值法，如熵权法，权重由原始数据所包含的信息量大小来确定[11]。为了使评价结果更符合实际，根据主、客观法的优点及缺点，本文结合层次分析法确定主观权重和权熵法确定客观权重相结合的方法确定指标权重[12]。

3.1 层次分析法确定主观权重

层次分析法是采用1～9级及其倒数的评定标度来描述各要素相对重要性的一种方法[13]。判断矩阵主要由专家判定，记此判断矩阵为M，并计算判断矩阵特征值λ以及特征向量ω。在对特征向量ω进行归一化处理之前，首先要对判断矩阵M进行一致性检验，当其排序结果具有满意一致性的时候再进行归一化计算，从而得到权重向量W1。

3.2 权熵法确定客观权重[14]

首先对判断矩阵归一化处理后得到判断矩阵V=(vij)。确定评价指标的熵值Hi：

(11)

最后对熵值进行归一化处理得到客观权重W2：

(12)

3.3 确定组合权重W

组合权重计算公式：

(13)

W=(WZ1,WZ2,…,WZm)

(14)

4 实例分析

本文选择的研究对象为位于吉林市平原区的8眼监测井的水质实测资料。吉林市位于吉林省中部偏东，地处长白山区向松嫩平原过渡地带，地貌类型较为复杂。研究区内水系发育，由松花江、拉林河及牡丹江3个水系的部分河段及支流组成，水利资源蕴藏量较为丰富。气候属温带大陆性季风气候，四季分明，夏季温热多雨，冬季寒冷干燥。

4.1 权重的确定

专家对地下水水质因子权重的评估结果见表1。

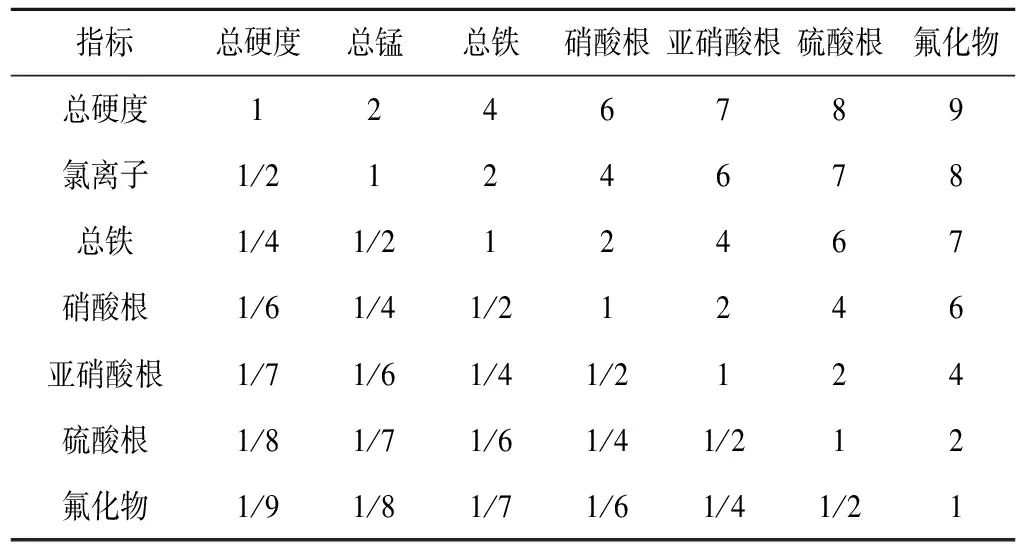
表1 地下水水质因子权重评估结果Tab.1 Weights assessment results of groundwater quality

根据表1建立判断矩阵，采用Matlab计算判断矩阵的最大特征值，特征向量λmax=(0.780 9，0.498 4，0.303 6，0.180 2，0.105 3，0.064 2，0.044 4)。一致性比率CR=0.04<0.08，说明排序结果满意一致性较好。因此可以进行归一化处理，处理结果W1=(0.395 0，0.252 1，0.153 6，0.091 15，0.053 26，0.032 47，0.022 46)。采用熵权法确定客观权重，根据公式(7)计算结果熵值权重向量W2=(0.088 3，0.223 4，0.164 8，0.141 6，0.132 4，0.135 6，0.113 9)。最后根据公式(10)计算组合权重，结果为W=(0.208 0，0.264 5，0.177 2，0.126 6，0.093 5，0.073 9，0.056 3)。

4.2 基于“垂面距离”的TOPSIS方法----正交投影法

吉林市各监测井水质数据及地下水质量分级标准见表2、表3。

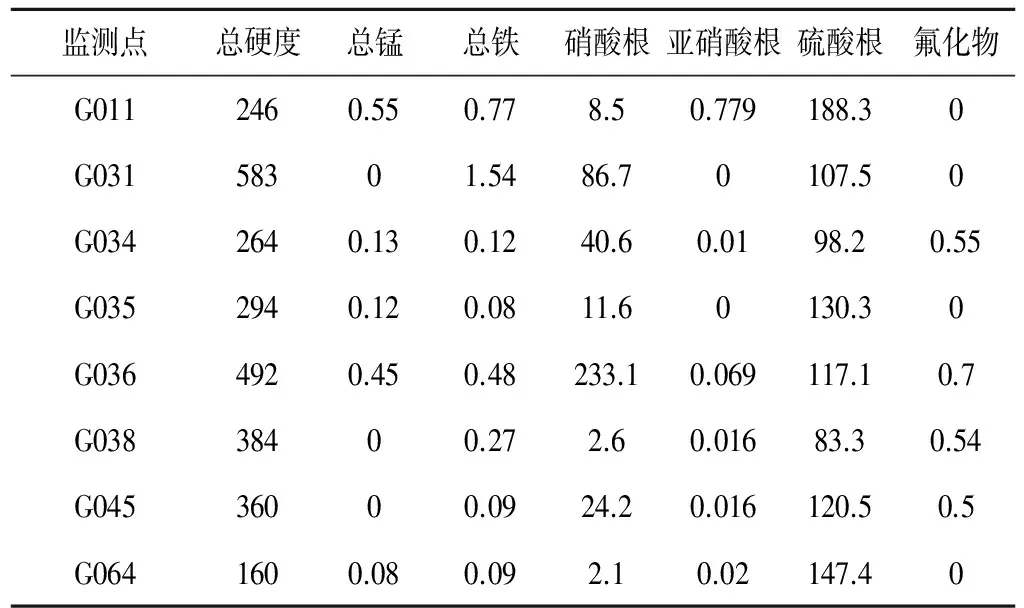
表2 吉林市各监测井水质监测结果 mg/L

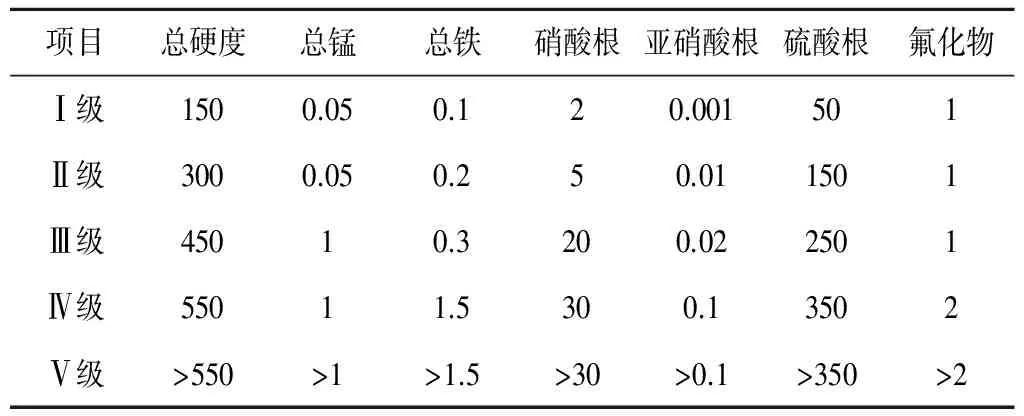
表3 地下水水质分级标准 mg/L

将5个评价指标的限值作为增广矩阵参与本次运算，并建立评价矩阵A，根据式(1)、(2)构建加权标准化矩阵Rij。

为了方便运算，根据文献[9]，将标准化矩阵每行、每列乘以相同的倍数P，正交投影法的评估结果将扩大P2，不影响排序，评价结果不变。将Rij每行、每列同乘以100，得到矩阵Mij，根据(3)得到正理想解,将Mij平移至正理想解处，根据式(4)、(5)、(6),可计算出各监测点和各指标分级标准限值与正理想解的“垂面距离”，结果见表4、表5。

表4 各监测点水质实测值与正理想解的“垂面距离” Tab.4 “Vertical distance” between each water quality measure data and positive ideal solution

表5 各分级标准与正理想解的“垂面距离” Tab.5 “Vertical distance” between each classification standard limits and positive ideal solution

将各监测点水质实测值及水质等级限值的垂面距离进行排序，由此可以得出基于“垂面距离”的TOPSIS方法----正交投影法的水质评价结果，见表6。

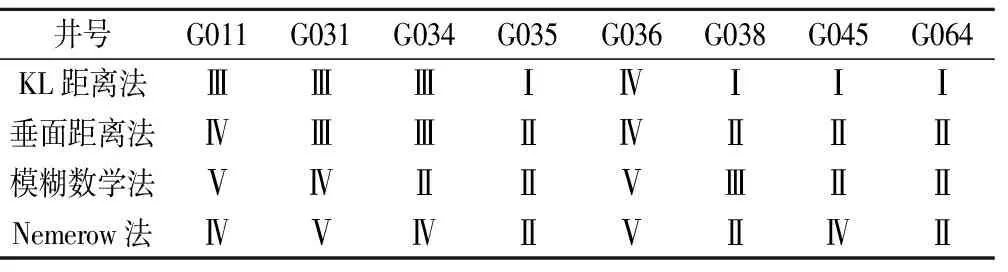
表6 几种水质评价方法评价水质的评价结果对比Tab.6 Comparison of the evaluation results of several water quality evaluation method

4.3 基于Kullback-Leibler距离的TOPSIS方法----相对熵排序法

基于Kullback-Leibler距离的TOPSIS方法评价地下水水质的计算过程中的前2步：构建增广矩阵、加权标准化增广矩阵，与上述正交投影法评价地下水水质的计算过程中前2步相同。根据公式(7)、(8)，可计算得各监测点的各个指标实测值及各级评价指标的限值与正、负理想解之间的距离，根据公式(9)可得出各个指标实测值及各级评价指标的限值与理想解的相对贴近度，见表7、8。

表7 各分级标准限值与理想解的相对贴近度Tab.7 Relative closeness between each classification standard limits and ideal solution

表8 各检测点水质实测值与理想解的相对贴近度Tab.7 Relative Closeness between each water quality measure data and Positive ideal solution

将各监测点水质实测值及水质等级限值与理想解的相对贴近度进行对比排序，由此可得出基于Kullback-Leibler距离的TOPSIS方法----相对熵排序法的水质评价结果，见表6、图2。

图2 几种水质评价方法评价水质的评价结果对比Fig.2Comparison chart of the evaluation results of several water quality evaluation method

4.4 综合分析

为了验证2种改进的TOPSIS法在地下水水质评价中的评价结果的准确性，本文引入Nemerow法及模糊数学法，将此4种方法的评价结果对比分析，见表6及图2，同时把水质级别Ⅰ、Ⅱ、Ⅲ、Ⅳ以及Ⅴ转化为数字1、2、3、4以及5，以便做折线图，使对比结果更直观。由图2可知，从总体上来说，基于“垂面距离”的TOPSIS方法----正交投影法与Nemerow法及模糊数学法的评价结果较为接近，大部分评价结果差异控制在一个等级之内，水样G031及G045的Nemerow法评价结果稍高，原因是Nemerow指数没有考虑每个因子的权重。虽然有些评价结果的差异在2个等级，但是可以综合Nemerow法、模糊数学法及基于“垂面距离”的TOPSIS方法，来对水质数据更加客观地评价分析。然而基于Kullback-Leibler距离的TOPSIS方法----相对熵排序法与上述3种方法在大部分监测点的评价结果相差较大，主要表现为评价结果等级普遍偏低，水质普遍偏优，说明此方法存在其自身的弊端，有一定的适用范围，并不能适用于所有水质评价。

5 结论

通过实例证实，采用主客观相结合的赋权法对评价对象进行赋权，并且以“垂面距离”替代传统的欧式距离对地下水水环境状况进行评价，并与Nemerow法及模糊数学法的评价结果作对比分析，此3种方法的评价结果较为接近，可以在地下水水质评价中相互对比分析。基于“垂面距离”的TOPSIS方法----正交投影法为地下水水质评价提供一种新方法。但是以Kullback-Leibler距离来替代传统的欧式距离对地下水水环境状况进行评价，得到的评价结果等级普遍偏低，有一定的适用范围，没有普适性，其适用条件还需作进一步研究分析。

[1] 肖长来，梁秀娟. 水环境监测与评价[M]. 北京：清华大学出版社，2008.

[2] 厉艳君，杨木壮. 地下水水质评价方法综述[J]. 地下水，2007，29(5)：19-24.

[3] GB/T 14848-93，地下水质量评价标准[S].

[4] 王先甲，汪磊. 基于马氏距离的改进型TOPSIS在供应商选择中的应用[J]. 控制与决策，2012，27(10)：1 566-1 570.

[5] 王玲玲，卢晓宁. 改进TOPSIS方法在大气环境质量评价中的应用[J]. 环境工程，2014,(9)：142-146.

[6] 黄强，屈吉鸿. 熵权和正交投影改进的TOPSIS 法优选水库特征水位研究[J]. 水利发电学报，2009，28(2)：35-40.

[7] 屈吉鸿，陈南祥. 改进的逼近理想解在地下水资源承载力评价中的应用[J]. 水利学报，2008，39(12)：1 309-1 315.

[8] 王晓峰. 涪江古城水库规划设计方案优选研究[D].西安：西安理工大学，2009.

[9] 华小义，谭景信. 基于“垂直”距离的TOPSIS法----正交投影法[J]. 系统工程理论与实践，2004(1)：114-119.

[10] 赵萌，邱菀华.基于相对熵的多属性决策排序方法[J]. 控制与决策，2010，25(7)：1 098-1 104.

[11] 张军，梁川. 基于灰色关联系数矩阵的TOPSIS模型在水环境质量评价中的应用[J]. 四川大学学报(工程科学版)，2009，41(7)：97-101.

[12] 乔雨，梁秀娟，王宇博，等.组合权重模糊数学法在水质评价中的应用[J]. 人民黄河，2015，37(5)：77-79.