动生感应中的“收尾加速度”问题分析

重庆 张大洪

动生感应中的“收尾加速度”问题分析

重庆 张大洪

抓变因、析过程，由“变”到“定”看分明。

在动生感应中导体棒切割磁感线运动产生感应电流，同时受到安培力的作用，由于导体棒的速度变化导致安培力变化，因而导体棒运动过程中的加速度均将发生相应变化。当在一定条件下导体棒最终将做匀变速直线运动时，我们将其不变的加速度称作“收尾加速度”。下面我们从实例来分类讨论这个“收尾加速度”。

一、由电容器的充电来维持的匀加速收尾过程

【例1】如图1所示，U形光滑导线框架宽L＝1m与水平面成θ＝30°角倾斜放置在竖直向上的匀强磁场中，磁感应强度B＝0.2T；在框架上垂直框边放一根质量m＝0.8kg，电阻r＝0.08Ω的导体棒ab；图中一个C＝5F的电容器连接在框架上，导体框架的电阻不计。现将ab棒从静止释放让它沿框架无摩擦下滑，设框架足够长且取g＝10m/s2。求：

图1

（1）棒从静止释放后将做什么运动，最终的加速度是多少？

（2）棒从静止释放沿框面下滑9.854m时的速度及所经历的时间。

【分析】棒ab释放后，在重力作用下加速沿框面下滑而切割磁感线，产生感应电动势E并对电容器充电，从而形成从b向a的充电电流；根据左手定则可以确定出棒所受到的安培力的方向及导体棒的受力如图2所示。

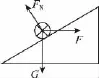
图2

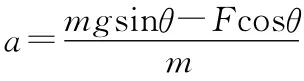
（2）棒从静止以a＝4.11m/s2做匀加速直线运动，经过9.854m的速度为，经历的时间

二、由电阻的相应变化来维持的匀加速收尾过程

【例2】图3中AB、CD是两根特制的完全相同的电阻丝，竖直固定在地面上，上端用电阻不计的导线连接，两电阻丝间距为L，有一根质量为m，电阻不计的金属棒ab跨在AC两点间的x轴原点处，并与电阻丝接触良好且无摩擦，空间有垂直纸面向里的匀强磁场B，金属棒释放后将向下滑动。求

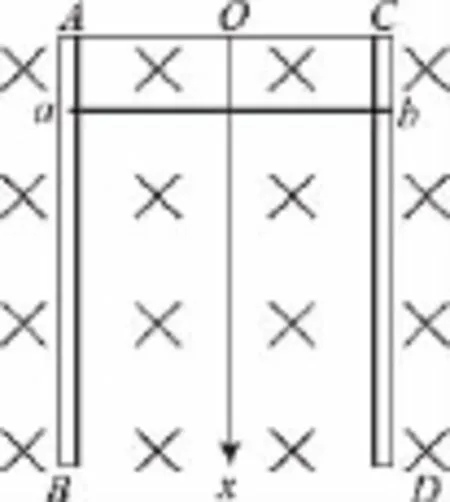
图3

（1）若电阻丝的阻值跟位移x的平方根成正比，即，试用假设法证明棒的下滑是匀变速直线运动；

（2）在棒做匀加速直线运动时，若L＝1m，B＝1T，，求：

（a）棒的加速度的大小；

（b）棒下落1m位移过程中流过的电量q；

（c）棒下落1m位移过程中电阻上的电功。

解得棒的加速度为a＝1.855m/s2；

（c）棒下落过程中电路的电阻相应增大，因而其消耗的电能应当从能量的转化与守恒定律得出

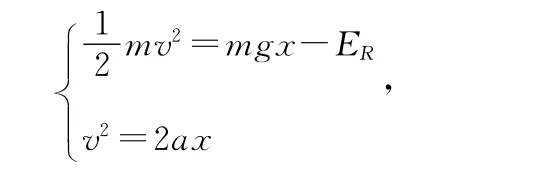
即max＝mgx-ER，则ER＝mx（g-a），

故此过程中电阻上的电功为

ER＝［1×1×（10-1.855）］J＝8.145J。

三、由两个导体棒间的相互制约而维持的匀加速收尾过程

【例3】如图4所示两根平行的金属导轨固定在同一水平面上，磁感应强度B＝0.5T的匀强磁场与导轨平面垂直，导轨电阻不计，导轨间距L＝0.2m；两根质量均为m＝0.1kg、电阻均为0.2Ω的平行金属杆甲、乙可在导轨上垂直于导轨滑动，与导轨间的动摩擦因数均为μ＝0.5。现有一与导轨平行、大小为F＝2N的水平恒力作用于甲杆使金属杆在导轨上滑动。求：

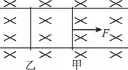
图4

（1）分析甲、乙两杆的运动的情况；

（2）杆运动很长时间后开始，则再经过5s两杆间的距离变化了多少？

四、由外力的变化维持的匀变速收尾过程

【例4】图5中两条相互平行的光滑金属导轨位于水平面内，间距L＝0.2m，在导轨的一端接有阻值为R＝0.5Ω的电阻；在x≥0区域有一与水平面垂直的均匀磁场B＝0.5T。一质量为m＝0.1kg的金属杆垂直放置在导轨上并以v0＝2m/s的初速度进入磁场中，在安培力及垂直于杆的水平外力F共同作用下做匀变速直线运动，加速度大小为a＝2m/s2，方向与初速度方向相反。设导轨及金属杆的电阻均不计且接触良好。求：

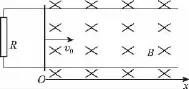
图5

（1）电流为0时金属杆所处的位置；

（2）电流为最大值的一半时施加在金属杆上外力F的大小及方向；

（3）保持其他条件不变而初速度v0取不同值，则开始时外力F的方向与初速度v0取值的关系。

【分析】由题意知杆必向右做匀减速直线运动到速度为0后再向左做匀加速直线运动直到离开磁场区域，故电流为0时表示杆的速度为0。

（2）杆的运动速度变化时，电路中的电动势变化，故电流相应变化，由电动势E＝BLv知杆运动的速度最大，则电路中感应电动势最大、电流最大，即最大电流必为；当电流为最大值的一半时，即

①若此时杆向右运动，则外力方向不定，我们假设外力F水平向右，由牛顿定律有F安-F＝ma，即F＝F安-ma＝ILB-ma＝-0.18N，故杆向右运动中外力F大小为0.18N，方向水平向左；

②若此时杆向左运动，则外力F方向必水平向左且有F-F安＝ma，即F-ILB＝ma，代入数据得F＝0.22N。

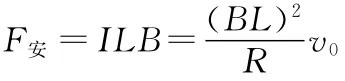
（作者单位：重庆市潼南第二中学校）