考查气体实验定律的六种模型例析

河南 王春旺

考查气体实验定律的六种模型例析

河南 王春旺

六种模型，考查重点。

气体实验定律（包括玻意耳定律、查理定律、盖-吕萨克定律、理想气体状态方程）是热学的重点内容，也是高考考查的重点。通过对近年高考试题分析，可归纳出高考对气体实验定律的考查主要有六种模型。

一、气缸类模型

【例1】（2016·海南卷）如图1所示，密闭气缸两侧与一U形管的两端相连，气缸壁导热；U形管内盛有密度为ρ＝7.5×102kg/m3的液体。一活塞将气缸分成左、右两个气室，开始时，左气室的体积是右气室的体积的一半，气体的压强均为p0＝4.5×103Pa。外界温度保持不变。缓慢向右拉活塞使U形管两侧液面的高度差h＝40cm，求此时左、右两气室的体积之比。取重力加速度大小g＝10m/s2，U形管中气体的体积和活塞拉杆的体积忽略不计。

图1

【解析】设初始状态时气缸左气室的体积为V01，右气室的体积为V02；当活塞至气缸中某位置时，左、右气室的压强分别为p1、p2，体积分别为V1、V2，由玻意耳定律得

联立①②③④式，并代入题给数据得

【点评】气缸类问题，一般涉及气缸、活塞、气体等，活塞为力学研究对象，气体为热学研究对象。对于导热气缸，一般可认为气体的温度不变（与外界温度相同）；对于绝热气缸，可认为与外界没有热交换，即Q＝0）。

二、液柱类模型

【例2】（2016·全国卷Ⅲ）一U形玻璃管竖直放置，左端开口，右端封闭，左端上部有一光滑的轻活塞。初始时，管内汞柱及空气柱长度如图2所示。用力向下缓慢推活塞，直至管内两边汞柱高度相等时为止。求此时右侧管内气体的压强和活塞向下移动的距离。已知玻璃管的横截面积处处相同；在活塞向下移动的过程中，没有发生气体泄漏；大气压强p0＝75.0cmHg。环境温度不变。

图2

【解析】设初始时，右管中空气柱的压强为p1，长度为l1；左管中空气柱的压强为p2＝p0，长度为l2。活塞被下推h后，右管中空气柱的压强为p′1，长度为l′1；左管中空气柱的压强为p′2，长度为l′2。

以cmHg为压强单位，由题给条件得

根据玻意耳定律p1l1＝p′1l′1，

联立解得p′1＝144cmHg。

根据题意可得

根据玻意耳定律可得p2l2＝p′2l′2，

解得h＝9.42cm。

【点评】对于液柱类问题，一般通过两侧液柱的高度差确定气体的压强。两侧气体通过液柱关联，可通过液柱得出两侧气体压强之间关系。

三、关联类问题

【例3】如图3所示，两个可导热的气缸竖直放置，它们的底部都由一细管连通（忽略细管的容积）。两气缸各有一个活塞，质量分别为m1和m2，活塞与气缸无摩擦。活塞的下方为理想气体，上方为真空。当气体处于平衡状态时，两活塞位于同一高度h（已知m1＝3m，m2＝2m）。

图3

（1）在两活塞上同时各放一质量为m的物块，求气体再次达到平衡后两活塞的高度差（假定环境温度始终保持为T0）。

（2）在达到上一问的终态后，环境温度由T0缓慢上升到T，试问在这个过程中，气体对活塞做了多少功？气体是吸收还是放出了热量（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）？

【解析】（1）设左、右活塞的面积分别为A′和A，由于气体处于平衡状态，故两活塞对气体的压强相等，

在两个活塞上各加一质量为m的物块后，右活塞降至气缸底部，所有气体都在左气缸中

由热力学第一定律：ΔU＝W＋Q，W＜0，ΔU＞0，

所以Q＞0，在此过程中气体吸收热量。

【点评】关联气体是指两部分或多部分气体通过活塞或液柱关联。解答时需要分别研究各部分气体，找出它们压强、体积、温度之间的关系，对每一部分气体，分别运用气体定律列方程联立解答。

四、变质量模型

【例4】（2016·全国卷Ⅱ）一氧气瓶的容积为0.08m3，开始时瓶中氧气的压强为20个大气压。某实验室每天消耗1个大气压的氧气0.36m3。当氧气瓶中的压强降低到2个大气压时，需重新充气。若氧气的温度保持不变，求这瓶氧气重新充气前可供该实验室使用多少天。

【解析】设氧气开始时的压强为p1，体积为V1，压强变为p2（2个大气压）时，体积为V2

根据玻意耳定律得p1V1＝p2V2

重新充气前，用去氧气在压强p2下的体积为V3＝V2-V1，

设用去的氧气在压强p0（1个大气压）下的体积为V0，则有p2V3＝p0V0

设实验室每天用去的氧气在压强p0（1个大气压）下的体积为ΔV，则氧气可用的天数为N＝V0/ΔV

联立解得N＝4（天）。

【点评】变质量模型一般有五类：充气问题、抽气问题、灌气问题、漏气问题、用气问题。分析变质量问题，可以通过巧妙地选择合适的研究对象，把变质量问题转化为定质量问题，利用气体定律解答。

五、图象信息类

【例5】（2016·山西忻州一中等四校联考）一定质量的理想气体从状态A变化到状态B再变化到状态C，其状态变化过程的p-V图象如图4所示。已知该气体在状态A时的温度为27℃。

图4

（1）求该气体在状态B、C时的温度；

（2）该气体从状态A到状态C的过程中是吸热还是放热，传递的热量是多少？

（2）因为状态A和状态C温度相等，且理想气体的内能是所有分子的动能之和，温度是分子平均动能的标志，所以在这个过程中ΔU＝0，

由热力学第一定律ΔU＝Q＋W得Q＝-W。

在整个过程中，气体在B到C过程对外做功，

故W＝-pBΔV＝-200J。

即Q＝-W＝200J，是正值，所以气体从状态A到状态C过程中是吸热，吸收的热量Q＝200J。

【点评】对于图象信息类问题，要在理解图象物理意义的基础上，从图象中提取解题需要的信息。一般来讲，p-V图象与横轴所围面积表示气体做功，与纵轴平行的直线表示等容变化，与横轴平行的直线表示等压变化。

六、与实际问题相关类

（ⅰ）求在水下10m处气泡内外的压强差；

（ⅱ）忽略水温随水深的变化，在气泡上升到十分接近水面时，求气泡的半径与其原来半径之比的近似值。

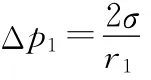
代入题给数据得Δp1＝28Pa。

（ⅱ）设气泡在水下10m处时，气泡内空气的压强为p1，气泡体积为V1；气泡到达水面附近时，气泡内空气压强为p2，内外压强差为Δp2，其体积为V2，半径为r2。

气泡上升过程中温度不变，根据玻意耳定律有

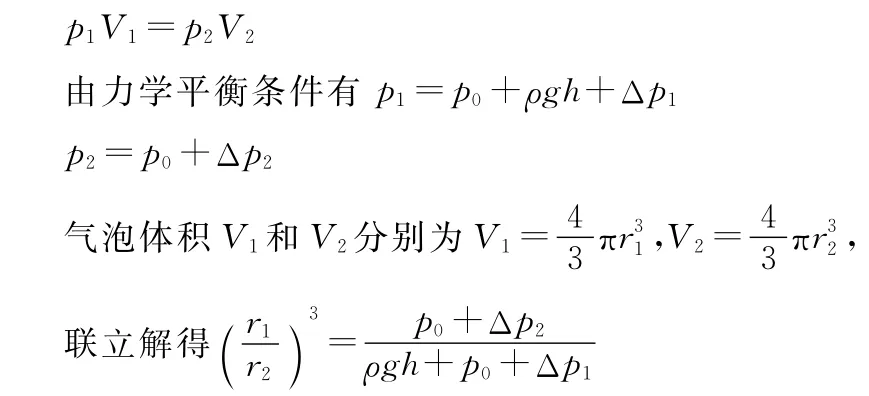
【点评】与实际相关类问题，可根据问题情景，建立恰当的模型。此题中的气泡缓慢上升，可认为是等温变化模型。根据题给条件，分别表示出初状态和末状态的压强、体积，利用玻意耳定律列方程解答。

（作者单位：河南省洛阳市第二中学）