在“翻转”中实现数学高效课堂——以人教版数学六年级上册《扇形的认识》教学为例

■武汉市经济技术开发区实验小学　叶　青



在“翻转”中实现数学高效课堂——以人教版数学六年级上册《扇形的认识》教学为例

■武汉市经济技术开发区实验小学叶青

“翻转课堂”无疑是当今教育的热门词。所谓“翻转课堂”，就是教师创建自学环境，学生提前在家或课外进行学习，回到课堂上再对教学的重难点进行交流，完成教学任务。这样的教学模式的转变凸显了以“学”为中心，旨在提高课堂效率，提升学生的自主学习能力和创新能力。这种教学模式的转变也引发了我的一些思考，如何在数学课堂中有效“翻转”而提高效率呢？

“翻转课堂”相较于传统的数学课堂，不仅仅表现在信息技术应用帮助预习这一方面，更大的变化是它所带来的新的教学理念的冲击，它完全颠覆了“教师的主体地位”，教师仅仅只是课堂的组织者和促进者。有了正确的定位，在让学生提前学习时，就要以“学生为中心”，从实际学情出发，以教材为蓝本，适度的重组教材，制定自主学习目标、导学单，帮助学生有效自学。

一、微课与导学单助力全境学习

要想真正“翻转”课堂，学生的提前学习必须是有效的，那么在制作微课和导学单时必须理清自学目标，知识的冲突点必须放在课堂上，以便于突破重难点。

在教学六年级《扇形的认识》这节课时，为了践行“生本理念”，我在导学单中清楚告知学生通过自学需要达到的自学目标：

1.认识弧、圆心角以及它们间的对应关系。

2.认识扇形，并能准确判断圆心角和扇形。

这两个目标通过微课的学习学生均能达成，而课堂中需要解决的教学目标则是理解扇形的概念（圆心角和弧的对应关系）及圆心角的大小和半径决定扇形的面积。

为了促进学生的有效自学，单单靠理清自学目标是不够的，必须有任务点的驱动，在观看完微课后完成相应练习就可以解决学生不落实自学的问题。在练习的完成过程中遇到障碍，还可以反复观看微课，真正的达到全境学习，落实“翻转课堂”的第一步。

根据该课的自学目标，我设计了以下的任务点：

练习1：

下图中哪些角是圆心角？

练习2：

下图中涂色的部分，哪些是扇形？

练习3：

以半圆为弧的扇形的圆心角是（）°

练习4：

判断：

（1）半径大的扇形面积大。（）

（2）圆心角为60°的扇形的面积比圆心角为15°的扇形面积大。（）

设计意图之一在于检测学生的掌握情况，之二在于根据学生的反馈情况制定课堂的冲突点，从而使课堂达到高效。

通过导学单的反馈发现：

1.学生对圆心角的判断掌握得非常好，没有一个学生判断错误。那是不是说明学生对圆心角的理解就到位了呢？课堂上如何检测这一结果呢？

2.扇形的判断出现了障碍，对于下面这个图形，学生的评判各占一半，那么对于扇形的概念理解问题究竟出现在哪呢？

二、深度辨析助力难点突破

在以往的教学中，常常会因为一些简单的知识的讲解浪费有限的课堂学习时间以及学生的有效注意时间，为了“照顾”一部分学生而“耽误”另外一部分学生，因此缺失了有效的“辨”和“探”。

在这节课的翻转课堂的实践中，我根据学生导学单呈现的情况进行分析梳理成课堂的辨析点：

1.学生对圆心角的判断都是正确的，那是否掌握了圆心角的概念了呢？我设计了这样的辨析问题，“这个角（图1）为什么不是圆心角？”学生开始发表自己的意见，“没有经过圆心”，这是他们通过自学对圆心角的理解。语言是思维的外衣，只有说的时候才能看出学生是否对这个知识点真正理解了。于是，我指着导学单中的另一个图继续追问“这个角（图2）经过了圆心，为什么你们也说不是圆心角呢？”看似简单的追问，其实是抓住了关键知识点在进行追问。经过这一追问，落实了学生对圆心角定义的理解，顶点在圆心的角才是圆心角。培养了学生语言表达的规范性，展示了数学学科的严谨性和逻辑性。因此，看似自学效果非常好的知识点，也要经过课堂的深度辨析才能让学生真正掌握。

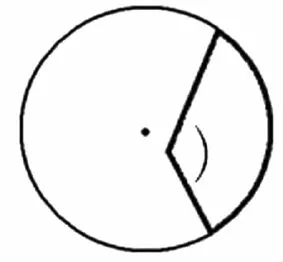
图1

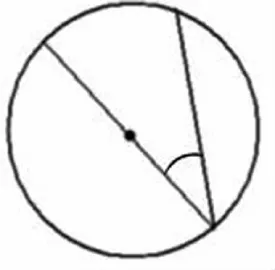
图2

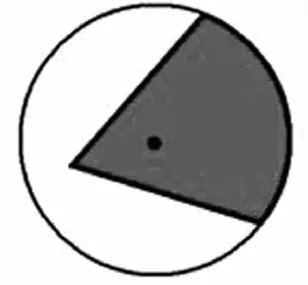
2．通过分析发现对于图3中的阴影部分是否为扇形，学生的判断各占一半。这便是课堂最好的辨析点，利用学生的兴趣点层层发问，“图4为什么不是扇形？”这个问题看似简单，其实是对学生的自学情况最好的检验。学生说：“两条边不相等。”貌似问题已经解决了，学生一语道破。再追问：“图3的两条边相等了啊，为什么有这么多同学觉得不是扇形？”“顶点不在圆心。”看来通过自学，基本达到了自学目标，但仔细观察会发现，认为这个是扇形的反而是成绩比较好的孩子，这个理由显然是不能说服他们的。于是第三轮追问：“看来这个理由似乎不能说服部分同学，你们来说一说为什么你们觉得是扇形？”“顶点只是不在这个圆的圆心，只要两边相等就肯定是另一个圆的圆心，那自然就是扇形。”一语激起千层浪，全班同学仿佛突然被点醒，纷纷附和：“是扇形，只是不是这个圆的扇形。”

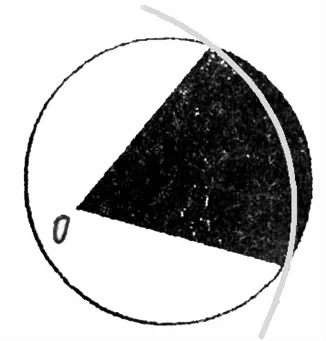
面对这种情况怎么处理呢？老师去解释？这恰恰正是让孩子“探”的机会。于是我说：“那究竟是哪个圆的扇形呢？以顶点为圆心，边长为半径你们画一画吧。”这一画就发现了问题，不是同一段弧了。（如图4）老师适时归纳，圆心角和对应的弧所围成的图形叫扇形。学生通过“探”才真正理解了圆心角和弧的对应关系，是不是扇形必须放在一个圆中才能进行判断。

在有效追问的作用下，学生的思维被充分打开，这些都有赖于前期的自主学习。教师再及时地把捕捉到的信息加以过滤与整合，充分合理的利用，使其成为课堂的深度辨析点。追问时，或正面直击，问在“难”处，突破教学难点；或旁敲侧击，问在“错”处，加深对本质认识；或顺势一抹，问在“深”处，历练数学思维；抑或拨云见日，问在“延”处，感悟数学思想。

三、灵动练习助力思维发散

概念理清之后，自然是要延伸应用的，“翻转”的目的也正在于使学生高效地获取知识并能灵活运用。于是我设计了一道“请画一个半径为2厘米，圆心角为100°的扇形”的操作题。此题灵动之处在于不同层次的孩子画扇形的方法是不一样的。大部分孩子先画半径为2厘米的圆，再去圆心角为100°的扇形，有些孩子则更为聪明，先画一个边长为2厘米的100°的角，再用圆规取边上画弧，这就简便多了。

在处理练习3中，也很好的体现了不同层次孩子的收获不同，由弧与圆周的关系延伸到圆心角与周角之间的关系，进而延伸到扇形面积与圆面积之间的关系。一路下来，学生的兴趣丝毫不减，带着意犹未尽的情绪结束了课堂。

课堂的结束并不意味着学习的结束，以上一系列的活动，层层深入，环环相扣，触发了学生参与学习的热情，激发了学生自主学习的能力。在对扇形的认识中从“模糊——清晰——深刻。深度辨析中生生互动，操作中“探”出究竟，课堂出现了真正的“翻转”与高效。

本课的有效尝试，实现了“翻转”的高效课堂。微课、导学单、深度辨析改变了传统的教学模式，使翻转课堂教学模式与学习方式深度融合，形成了有实效有高效的翻转课堂。“道不远人”，新的理念需要更多的实践行动。

责任编辑郑占怡