不定核大间隔聚类算法*

李　森，薛　晖+1.东南大学计算机科学与工程学院，南京2111892.东南大学计算机网络和信息集成教育部重点实验室，南京211189

* The National Natural Science Foundation of China under Grant No. 61375057 (国家自然科学基金); the Natural Science Foundation of Jiangsu Province under Grant No. BK20131298 (江苏省自然科学基金).

Received 2015-05,Accepted 2015-07.

CNKI网络优先出版：2015-08-11, http://www.cnki.net/kcms/detail/11.5602.TP.20150811.1521.005.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0112-10



不定核大间隔聚类算法*

李森1,2，薛晖1,2+
1.东南大学计算机科学与工程学院，南京211189
2.东南大学计算机网络和信息集成教育部重点实验室，南京211189

* The National Natural Science Foundation of China under Grant No. 61375057 (国家自然科学基金); the Natural Science Foundation of Jiangsu Province under Grant No. BK20131298 (江苏省自然科学基金).

Received 2015-05,Accepted 2015-07.

CNKI网络优先出版：2015-08-11, http://www.cnki.net/kcms/detail/11.5602.TP.20150811.1521.005.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0112-10

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

Key words: maximum margin clustering; indefinite kernel; semi-infinite program

摘要：受限于传统统计学习理论，大多数核方法都要求核矩阵半正定，但是在很多实际问题中这样的要求常常很难满足，由此产生了不定核。近年来，研究者们提出了一系列基于不定核的分类方法，取得了很好的性能，但是关于不定核聚类方法的研究相对较少，而且现有的核聚类算法基本上都是基于正定核而设计的，无法或者很难处理核矩阵不定的情况。针对此问题，以大间隔聚类（maximum margin clustering，MMC）模型为基础，提出了一种新的不定核大间隔聚类（indefinite kernel maximum margin clustering，IKMMC）算法。IKMMC算法旨在寻求一个正定核以逼近不定核，并将度量两者差异性的F-范数作为一个正则化项嵌入到MMC框架中。首先给定样本初始标记，然后迭代优化目标函数，并将每步迭代得到的样本预测错误率作为迭代终止条件。在每步迭代时，IKMMC算法进一步将目标函数转化为半无限规划（semi-infinite program，SIP）形式，并动态调整约束集进行交替优化。实验验证了IKMMC算法的有效性。

关键词：大间隔聚类；不定核；半无限规划

1　引言

核方法是机器学习领域的一种重要学习方法，其通过一个非线性映射函数将数据由低维空间映射到高维空间，以解决低维空间无法解决的分类问题。受限于传统的统计学习理论，大多数核方法要求核函数正定，并满足Mercer条件[1]，使得在再生核Hilbert空间（reproducing kernel Hilbert space，RKHS）[2]中内积与核函数之间一一对应，并导出凸优化问题，进而可获得全局最优解。然而，当为了提高方法性能而在正定核方法中嵌入先验知识时，往往会导致核函数不定。而且在很多现实问题中，使用不定核却能获得比正定核更好的性能。例如，在人脸识别中，Liu在核主成分分析（kernel principal component analysis，KPCA）方法中使用了不定的分数阶多项式核，取得了比使用正定多项式核KPCA更好的识别效果[3]。

近年来，研究者们提出了一系列不定核分类算法，大致可分为3类。第一类是对不定核矩阵做谱变换。其中包括将不定核矩阵负特征值置零的Clip变换方法[4]，对负特征值取反的Flip变换方法[5]以及将所有特征值与最小负特征值的绝对值之和作为新特征值的Shift变换方法[6]。第二类是直接使用不定核矩阵。例如，Lin等人对于非正定Sigmoid核支持向量机（support vector machine，SVM）的非凸对偶形式，提出了一种序列最小化方法以寻求稳定点[7]。 Haasdonk对不定核SVM给出了一个几何解释，并将相应的优化问题转化为伪欧氏空间中两凸包之间距离最小化问题[8]。Loosli等人将SVM拓展到Krein空间并直接对不定核矩阵进行操作，得到了比正定核更好的效果[9]。Alabdulmohsin等人将1-范式SVM拓展到不定核情况，保证了目标函数为凸，用不定核函数得到了较高准确率[10]。第三类是将不定核矩阵K0视作某个未知正定核矩阵K的加噪形式，将不定核中的优化问题替换为核矩阵的学习问题。Luss等人最早提出了这种学习框架，他们把K和K0的F-范数嵌入目标函数中，将不可微的目标函数进行二次平滑，分别采用投影梯度和中心点割平面方法[11]进行求解[12]。进一步地，Chen等人提出了用交替优化方法得到K的算法，将目标函数表达为一个半无限二次约束线性规划问题，通过迭代求解可最终收敛至一个全局最优解[13]。Chen等人视K为K0的谱修正，将K嵌入目标函数中，并把目标函数表达为二阶锥约束线性规划的形式求解[14]。Gu等人将KPCA刻画为一个核变换框架，并把不定核SVM嵌入该框架中联合求解，从而有效保持了核替代的一致性[15]。

尽管这些不定核方法效果很好，但大都用于分类，很少能解决基于不定核方法的聚类问题。大间隔聚类（maximum margin clustering，MMC）是基于核方法的经典聚类算法之一。Xu等人最先提出将SVM的最大化分类间隔准则应用到聚类问题中，并将基于这一准则的聚类算法称为大间隔聚类[16]。同SVM引入核方法解决数据在低维空间线性不可分问题相似，MMC也引入了核方法以求得到更好的聚类效果。为了实现MMC，Xu等人将其表达为一个整数规划问题，再通过放宽约束条件将其表达为一个半定规划问题，从而可以利用优化包进行优化。由于半定规划问题的求解复杂度较高，Zhang等人提出了基于交替优化的iterSVR算法[17]，其思想是先用简单的聚类算法（如k-means）给定初始类别标记，训练SVR （support vector regression）得到权向量，然后通过整数规划得到新样本标记，再将新标记作为输入，如此迭代直到算法收敛。Zhao等人进一步提出了用割平面方法和凹凸约束规划（constrained concave-convex procedure，CCCP）[18]优化MMC模型的算法[19]。该算法首先将约束集置空，用CCCP优化目标函数，然后选择最违反约束的条件加入约束集迭代优化，直到算法收敛。为了提高优化效率，Wang等人又提出了cpMMC（cutting plane MMC）算法[20]，先用CCCP将原问题分解为多个子问题，再用割平面算法优化子问题。Zhang等人提出SKMMC（sparse kernel MMC）算法[21]，将cpMMC拓展到非线性核情况。考虑到非凸问题只有局部最优解以及半定规划问题的复杂性，Li等人将样本标记松弛为其凸包，从而将非凸的整数规划问题松弛为凸问题并表达为凹凸规划的形式，通过割平面方法和多核优化方法优化该问题[22]。Wu等人进一步将该方法拓展到SVR模型[23]。不同于前述方法，Gopalan等人从样本点和间隔的关系出发，首先通过数据点在多条直线上的映射结果得到样本点间的相似度，然后通过NCut进行聚类，得到了较好的结果[24]。

虽然MMC算法的聚类效果很好，但均要求核正定。当核不定时，MMC算法无法应用。针对以上问题，本文以MMC为基础，提出了一个新的不定核大间隔聚类（indefinite kernel maximum margin clustering，IKMMC）算法，旨在寻求一个正定核以逼近不定核，并将度量两者差异性的F-范数作为一个正则化项嵌入到MMC框架中，为解决不定核聚类问题提供了一种可行思路。IKMMC算法首先给定样本初始标记，然后迭代优化目标函数，并将每次迭代时样本预测错误率作为迭代终止条件。优化目标函数时，IKMMC算法将其转化为半无限规划（semi-infinite program，SIP）形式，动态调整约束集进行交替优化。实验结果表明，该模型在核矩阵不定情况下能取得较好的聚类效果。

本文组织结构如下：第2章简单回顾MMC模型；第3章在MMC模型的基础上提出IKMMC模型，并给出该模型的具体优化算法；第4章在不同数据集上验证IKMMC算法的有效性，给出与简单谱变换不定核MMC以及基于高斯核的k-means算法的对比实验；最后对相关工作进行总结。

2　大间隔聚类

当核矩阵为对称半正定且将样本聚成两类时，给定样本X＝{x1，x2，…，xn}，MMC旨在寻找一个聚类超平面，使得聚类后不同标记的样本到该超平面的最小距离最大化，即寻找一个最大间隔。具体地，可以通过优化下式得到该超平面和样本标记：

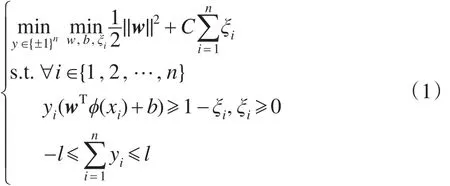
其中，ϕ是非线性映射函数，将数据由原始空间映射到高维空间：xi→ϕ(xi)，进而使样本可以在高维空间中聚类。式（1）中，w和b唯一确定该超平面，最后一个约束条件用来控制样本间的平衡，防止聚类后得到的间隔过大，影响聚类效果。

由于式（1）是关于标记y的整数规划，其相对于二次规划效率较低，故对式（1）进行变换[25]：

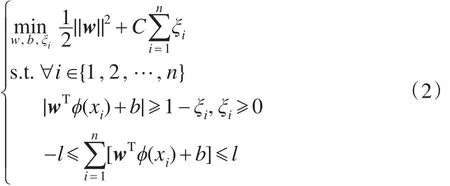
聚类后样本的标记通过yi＝sign(wTϕ(xi)＋b)得到，由此可将整数规划转化为二次规划求解。

3　不定核大间隔聚类算法

虽然MMC算法具有较好的聚类性能，但是当核矩阵不定时，无法应用MMC算法。因此，本文以MMC模型为基础，提出了一个基于不定核的大间隔聚类模型。

3.1模型构建

根据Mercer定理，当核矩阵K半正定时，样本点与其在Hilbert空间中的映射点存在如下映射：

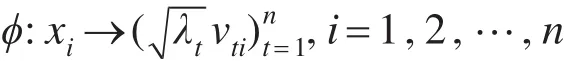
其中，λt是K的第t个特征值；vt是λt对应的特征向量。若K不定，样本点与Hilbert空间中的点不再一一对应。因此，为了在不定核情况下进行大间隔聚类，需要找到一个“最接近”原不定核的正定核。

最简单的方法是对不定核矩阵做谱变换，但是简单谱变换会丢失原不定核中有用的信息，进而影响算法的性能。因此，本文采用了正定核替换策略，将不定核矩阵K0看作某个未知正定核矩阵K的加噪形式，学习K以逼近K0，进而提出IKMMC模型：

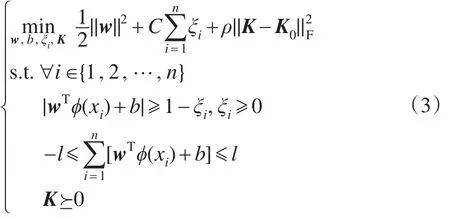
观察式（3）可知，与MMC模型不同的是，IKMMC模型的目标函数同时是K的非凸函数。样本标记由w、b以及K0的正定核逼近K共同确定，这增加了模型优化的难度。图1描述了IKMMC与其他聚类算法的关系。3.2节给出了该模型的具体优化方法。

3.2优化求解

IKMMC算法采取迭代优化方法：首先随机给样本赋初始标记，然后优化式（3），将第t步的输出标记作为第t＋1步的输入标记，并将每步迭代时样本预测的错误率（与输入标记相比）作为迭代终止条件。由此，不定核聚类问题转变为不定核分类问题的迭代过程。下式为第t＋1步的目标函数：

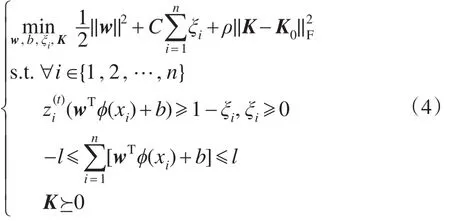
显然，式（4）相对于w、b和K均为凸函数，因此存在一个全局最优解。对(w，b，ξ)求对偶可得：

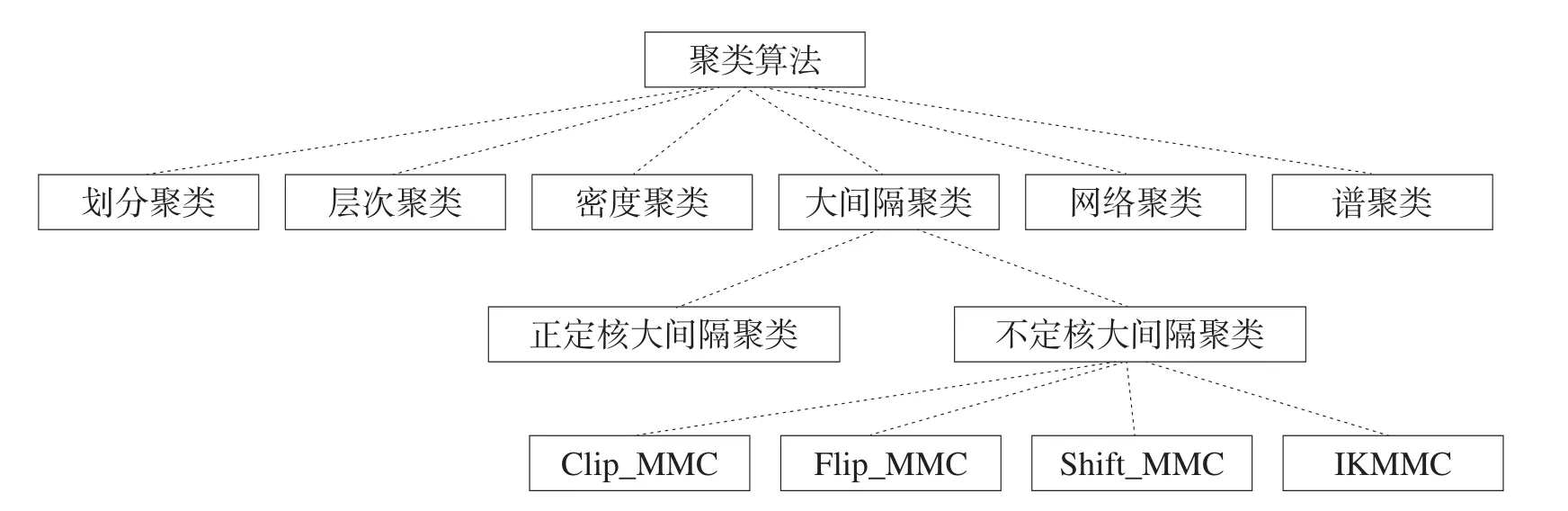
Fig.1 Relationship between IKMMC and other clustering algorithms图1　IKMMC与其他聚类算法的关系描述

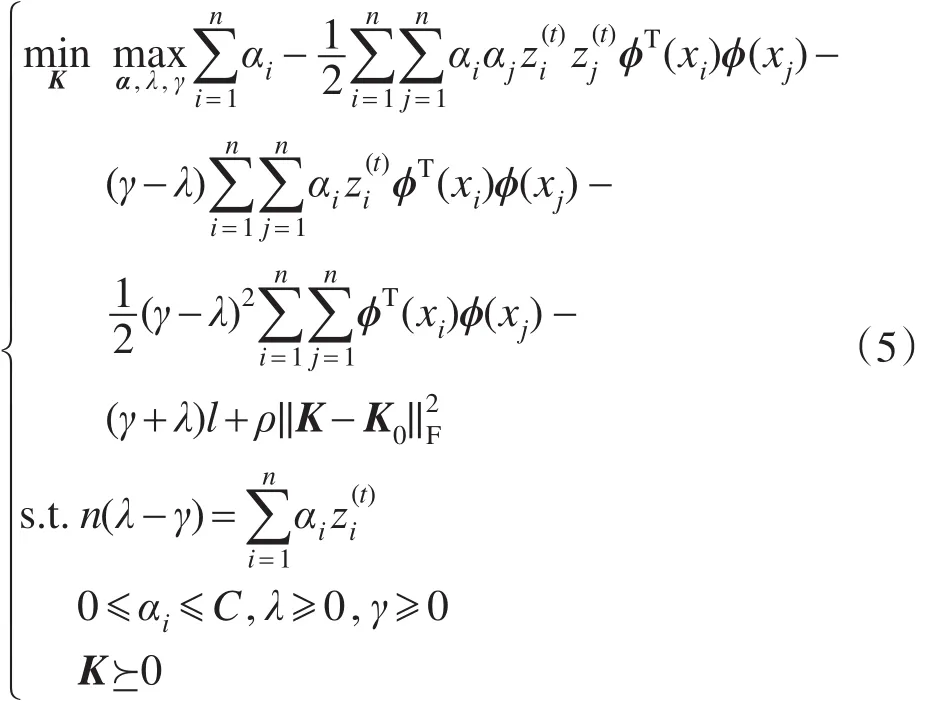
式（4）和式（5）都是凸二次规划问题且它们的对偶间隙为0，因此优化式（5）得到的解就是式（4）的最优解。令：

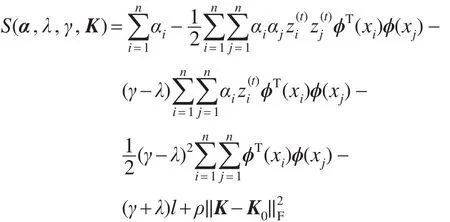
易知该最优解是由S(α，λ，γ，K)张成的超面上的一个鞍点，该点对K取极小值，对α、λ、γ取极大值。

设(α∗，λ∗，γ∗，K∗)为式（5）的最优解。对于任意满足式（5）约束条件的α、λ、γ、K有下式成立：

S(α，λ，γ，K∗)≤S(α∗，λ∗，γ∗，K∗)≤S(α∗，λ∗，γ∗，K)因为S(α，λ，γ，K)是关于K的凸函数，所以有：

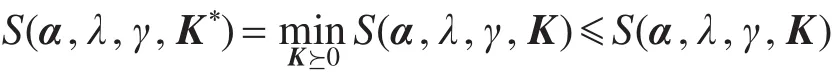
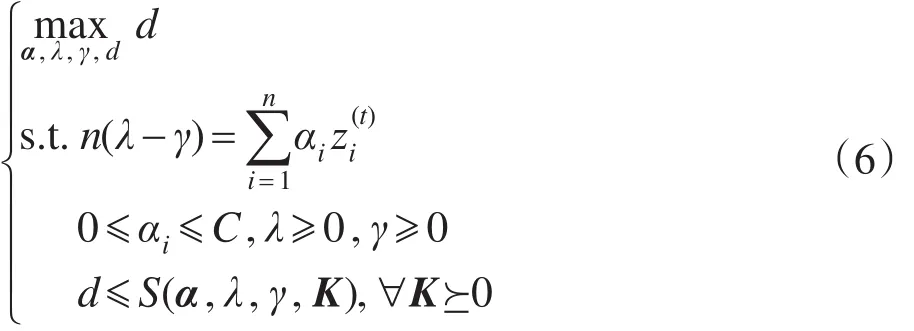
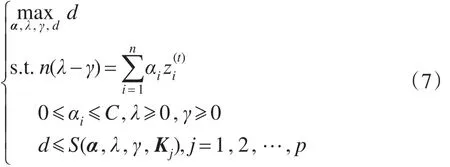
式（7）约束集是式（6）约束集的一个子集，随着式（7）中约束集合逐渐增加，式（7）的最优解逐渐逼近式（6）的最优解。通过更新约束集，优化式（7）可以逐步逼近“最优解”。SIP优化过程如图2所示。

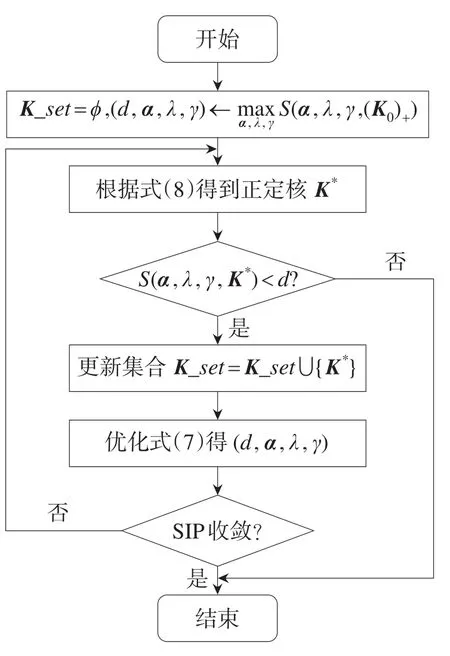
Fig.2 Flow chart of SIP图2　SIP优化流程图

SIP优化过程对应IKMMC算法步骤3～步骤13。求K∗以更新约束集时，有如下命题成立。

命题1给定(α，λ，γ)，K∗＝S(α，λ，γ，K)，则K∗可以通过如下公式得到：

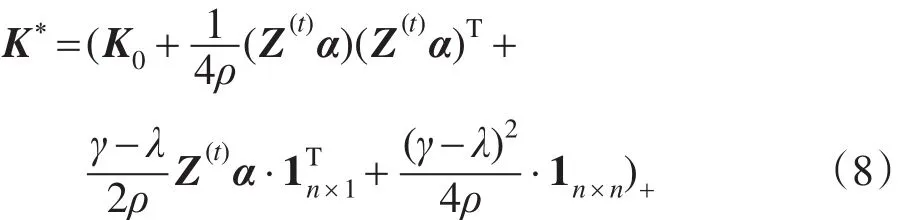
其中，Z(t)＝diag(，，…，)；1n×1表示n维全1列向量；X＋＝∑imax(0，λi)xi；λi和xi分别为X的第i个特征值和特征向量。

证明S(α，λ，γ，K)可以改写为如下形式：

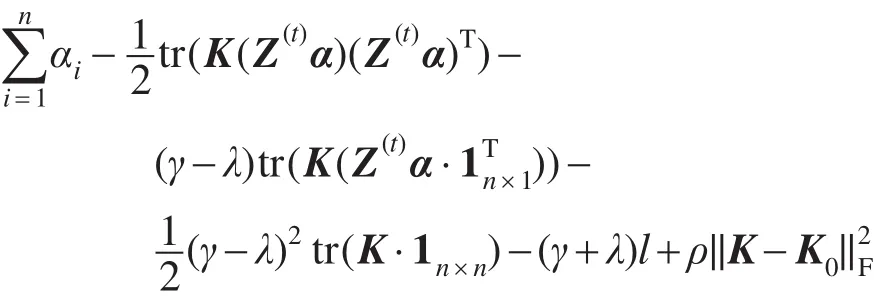
在当前(α，λ，γ)上，最优的K∗是通过优化S(α，λ，γ，K)得到的。由于(α，λ，γ，l)已知，且||K−K0＝tr((K−K0)T(K−K0))，则S(α，λ，γ，K)与下式等价：

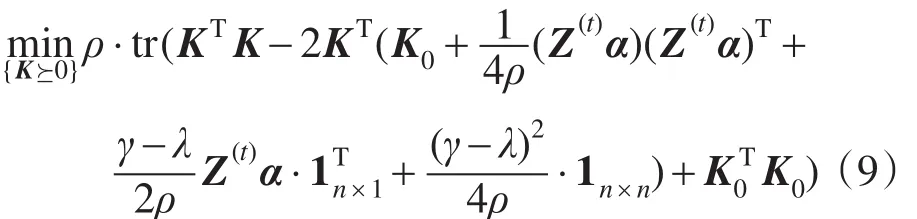
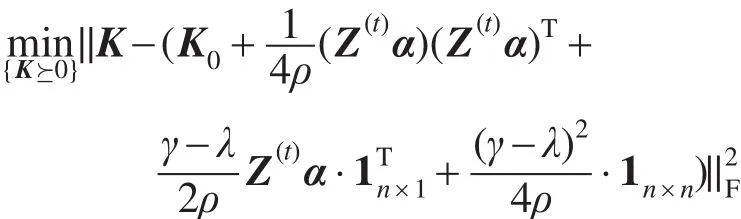
IKMMC算法的伪代码如下所示，算法的计算复杂度为O(n3)。

算法1 IKMMC算法

输入：不定核矩阵K0，惩罚因子C、ρ，类平衡参数l

输出：w，b，K

3.3算法分析

显然，式（7）的解是式（6）的一个近似解，有如下命题成立[13]：

命题2设(d∗，α∗，λ∗，γ∗)为式（6）的最优解，K∗为式（6）取最优解时的K。SIP在第i步时记＝S(αi−1，λi−1，γi−1，K)，f(i)＝S(αj−1，λj−1，γj−1，)，g(i)＝di＝S (α，λ，γ，Kj)，有不等式f(i)≤ d*≤g(i)成立，且f(i)单调递增，g(i)单调递减。

证明由于式（7）约束集是式（6）约束集的子集，故有如下关系成立：

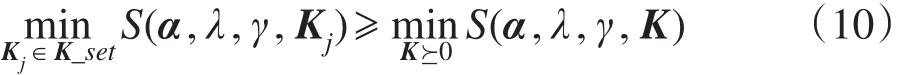
对式（10）两边关于α、λ、γ取极大值，因为式（6）的最优解是一个鞍点，所以有下式成立：

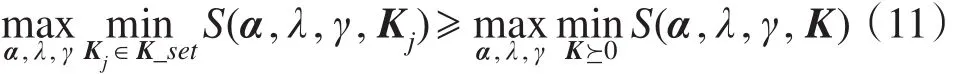
即g(i)≥d∗成立。

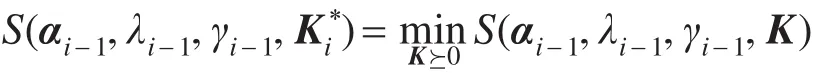
因此第i步求得的点S(αi−1，λi−1，γi−1，)位于集合Ω中，从而f(i)＝S(αj−1，λj−1，γj−1，)≤d∗。

根据式（7），SIP优化过程不停止迭代时，集合K_set都会加入，每加入一个，目标函数值减小一次，故g(i)单调递减。进一步根据f(i)的定义，可知f(i)单调递增。

由命题2可知，算法1内层迭代过程（步骤3～步骤13）中始终有f(i)≤d∗≤g(i)成立，且f(i)递增，g(i)递减，因此f(i)和g(i)间的间隙逐步缩小，即f(i)和g(i)逐步逼近d∗。当此间隙在有限步内迭代到小于某个预先给定的阀值时，步骤3～步骤13收敛。在外层循环，IKMMC将样本标记预测的错误率作为迭代终止条件，实验中算法基本在10步以内迭代至一个稳定点。

4　实验与分析

给定不定核K0，对其进行特征值分解K0＝UΛUT。将Λ负特征值置零可得Λclip，Kclip＝UΛclipUT即为Clip变换后得到的半正定核，基于该核的MMC算法记作Clip_MMC。类似地，对负特征值求绝对值可得Flip_MMC，对Λ中每个特征值加上最小特征值的绝对值得到Shift_MMC。为了检验IKMMC算法的聚类效果，本文将其与上述3种谱变换MMC算法以及基于高斯核的K-means算法（KKM）在基准数据集上进行了比较。

表1给出了实验中使用的数据集。其中，Ionosphere、Image、Diabetis、Wdbc均是来自UCI[27]的两类数据集。DNA数据集是一个生物数据集[28]，包含3类样本，实验选择其中样本数目相当的两类数据。

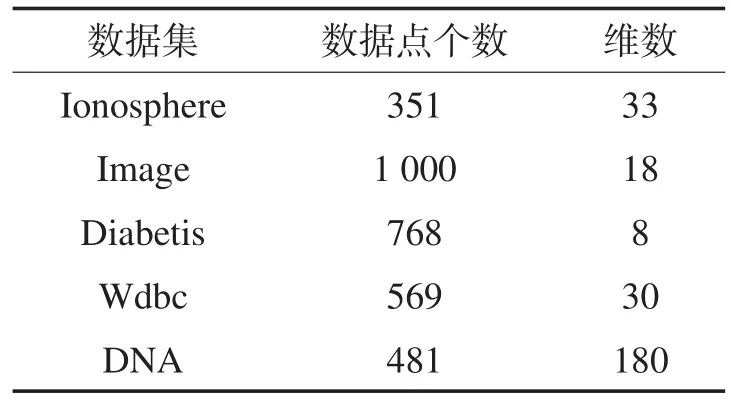
Table 1 Data characteristics of benchmark datasets表1　数据集数据特征

为了得到不定核矩阵，实验中先用高斯核生成半正定核矩阵，然后向其中加入随机扰动r∗(E＋ET)/2，其中，E是均值为0的单位协方差矩阵，r为扰动因子，r＝0.1。核函数的参数σ、惩罚因子C以及正则化因子ρ均由交叉验证确定。若数据集中正负样本数目相当，则平衡参数l取0.03n，否则取0.3n，其中n是样本个数。

实验中以聚类错误率和Rand Index（RI）作为评价聚类算法性能的准则。

错误率的计算方式如下：

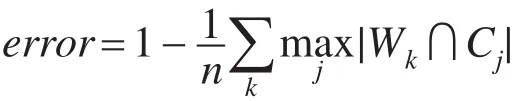
其中，Wk为通过聚类算法得到的样本子集；Cj为按照样本原始标记得到的子集。各聚类算法在不同数据集上的错误率如表2所示。

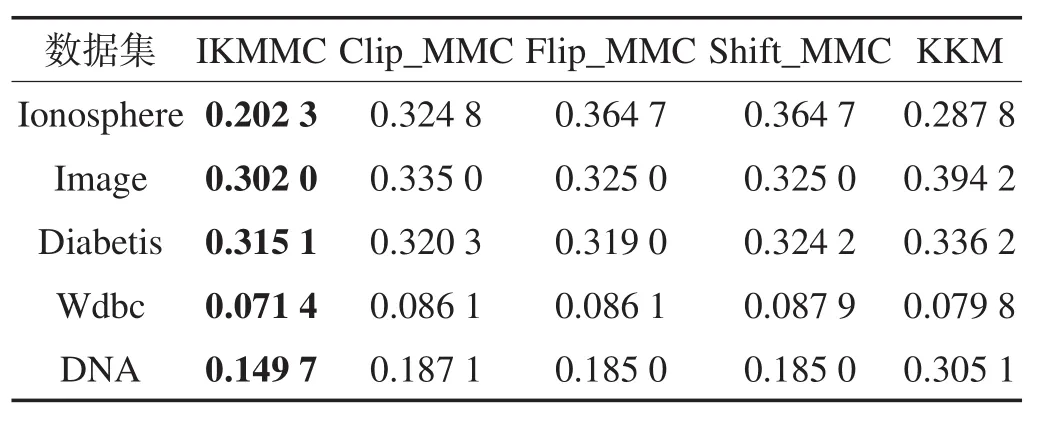
Table 2 Clustering errors on various datasets表2　聚类算法在不同数据集上的错误率

RI计算方式如下：

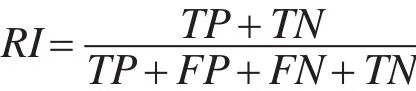
其中，TP表示标记相同被聚到同一簇的样本个数；TN表示标记不同被聚到不同簇的样本个数；FP表示标记不同被聚到同一簇的样本个数；FN表示标记相同被聚到不同簇的样本个数。各算法在不同数据集上的RI值如表3所示。

Table 3 Rand Indices on various datasets表3　聚类算法在不同数据集上的RI值

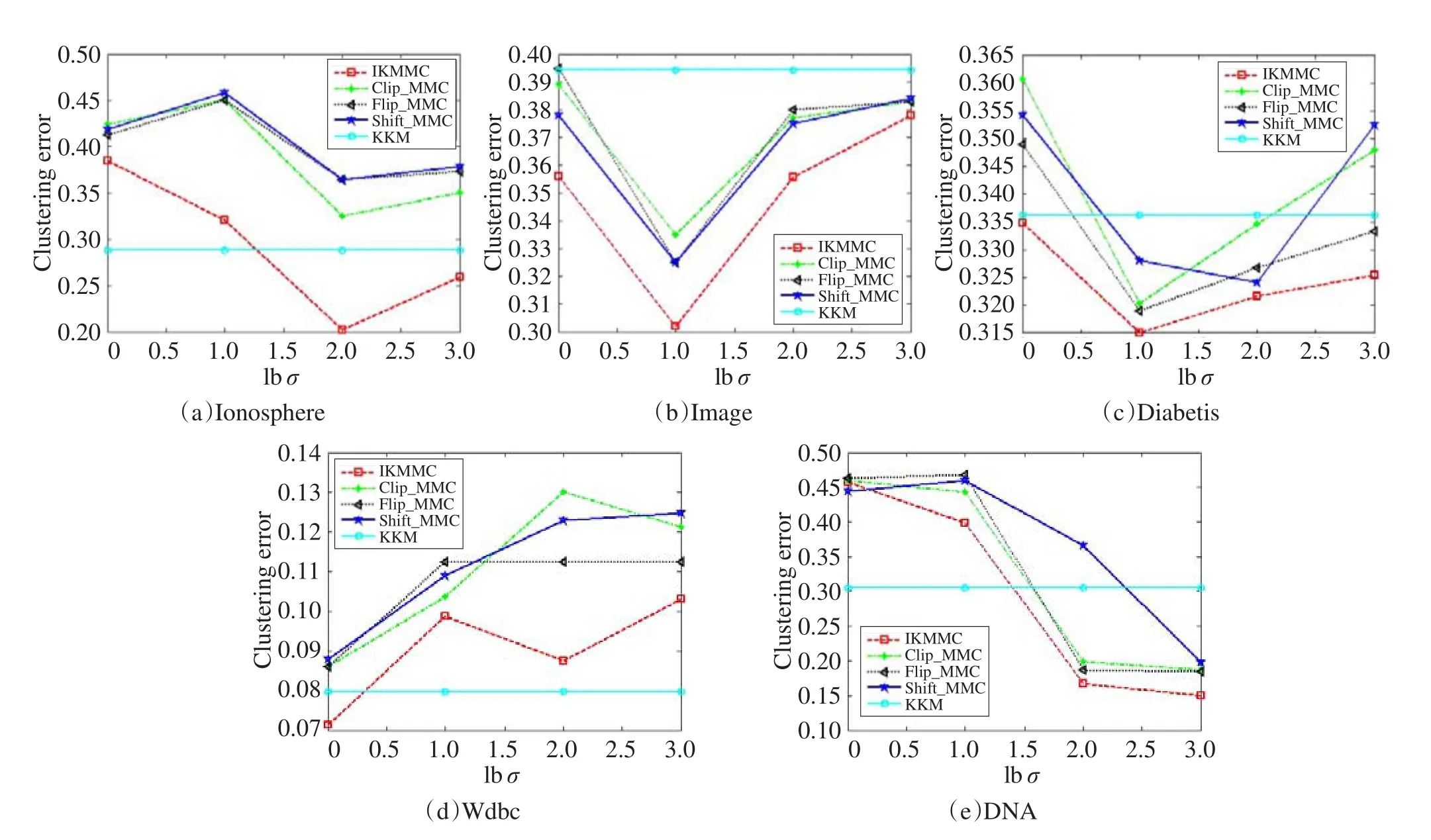
Fig.3 Clustering errors with various values for σ on various datasets图3　算法在各数据集上聚类错误率随σ的变化关系

由表2可见，IKMMC算法在所有数据集上的错误率均低于其他对比算法。特别地，在Ionosphere数据集上，IKMMC算法的错误率比谱变换得到的3种MMC算法和KKM算法低8%～16%。在DNA数据集上，4种不定核MMC算法与KKM相比，错误率低12%以上。此外，在其他3个数据集上，IKMMC比其他3种不定核MMC算法低4%左右。由表3可见，IKMMC 在RI指标上亦优于其他4种算法。这说明在复杂的实际问题中，使用不定核能得到比正定核更好的性能。

图3和图4分别给出了各算法在不同数据集上的聚类错误率随主要参数σ和C的变化关系。从图3可以看出，5种算法错误率随着σ的变化，均呈现一定程度的震荡。但是在Image和Diabetis数据集上，IKMMC算法的错误率始终低于其他算法。在其他3个数据集上，IKMMC算法均达到了最小值。由于KKM算法与参数C无关，故图4描述了IKMMC、Clip_MMC、Flip_MMC、Shift_MMC算法与C的变化关系。由图4可见，各算法在不同数据集上的错误率整体上随C的增大而增大。其中，在Ionosphere和DNA数据集上，IKMMC的错误率全面低于其他3种算法。在Diabetis、Image和Wdbc数据集上，IKMMC算法错误率也基本小于其他3种算法，且在C的变化区域达到了最小值。因此，基于正定核替换策略的IKMMC模型比谱变换得到的MMC模型有更好的聚类效果。

5　结束语

本文以MMC模型为基础，通过向其目标函数中嵌入度量正定核与不定核差异性的F-范数，寻求正定核以逼近不定核，提出了基于不定核的大间隔聚类模型IKMMC及其聚类算法。该算法首先给定样本一组初始标记，然后迭代优化IKMMC模型，并将预测错误率作为判断算法迭代终止的条件。在每步迭代时，IKMMC将目标函数转化为半无限规划形式，并动态调整约束集进行交替优化。实验验证了IKMMC算法具有较好的聚类效果。

下一步工作可以考虑将算法进一步拓展到多类情况，也可将单不定核的IKMMC拓展到多不定核情况以提高性能。

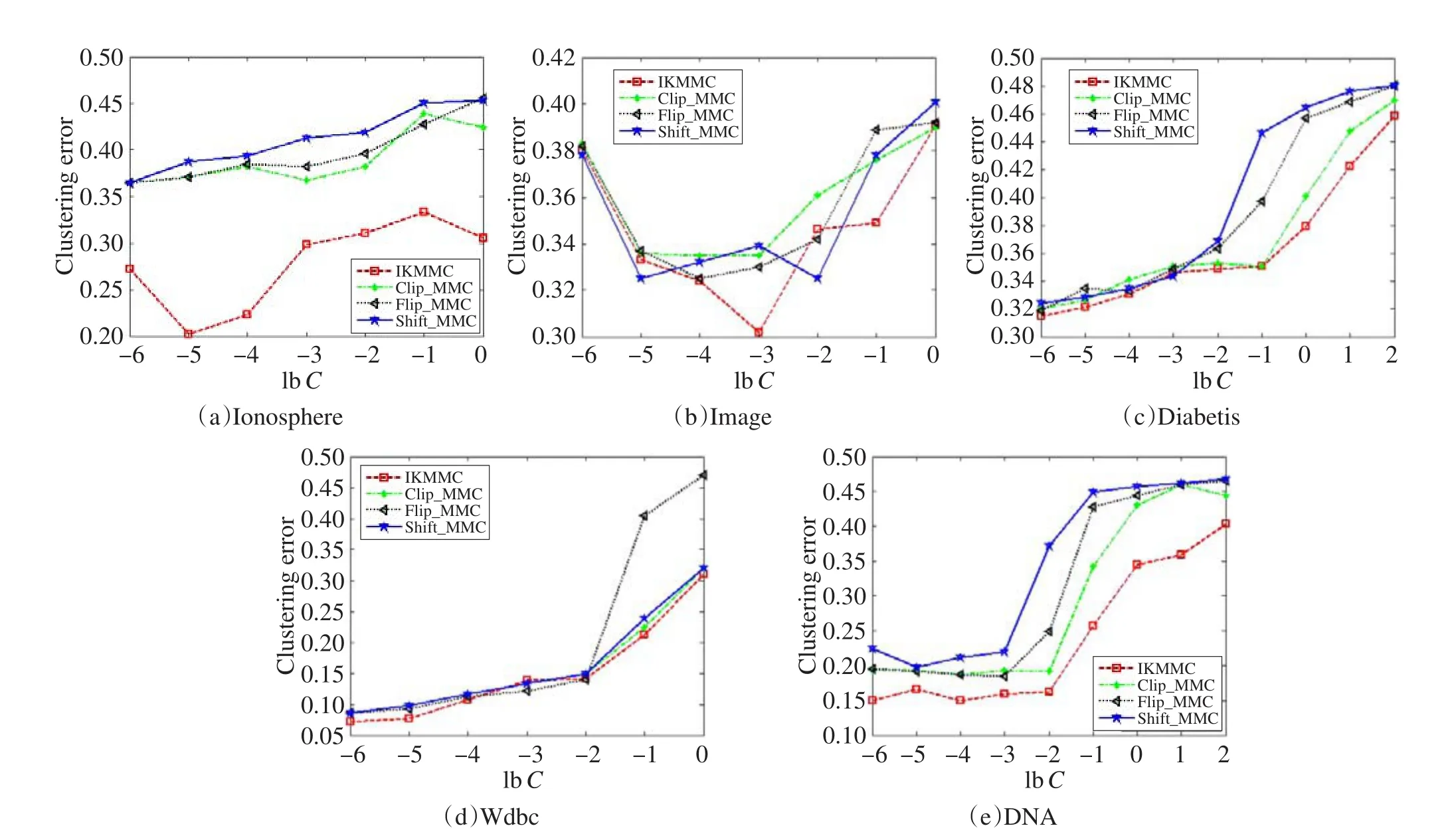
Fig.4 Clustering errors with various values for C on various datasets图4　算法在各数据集上聚类错误率随C的变化关系

致谢向对本文工作给予支持和建议的老师们表示感谢。

References:

[1] Cristianini N, Shawe-Taylor J. An introduction to support vector machines and other kernel-baesd learning methods[M]. Cambridge, UK: Cambridge University Press, 2000.

[2] Sum H. Mercer theorem for RKHS on noncompact sets[J]. Journal of Complexity, 2005, 21(3): 337-349.

[3] Liu Chengjun. Gabor-based kernel PCA with fractional power polynomial models for face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 572-581.

[4] Pekalska E, Paclik P, Duin R P W. A generalized kernel approach to dissimilarity-based classification[J]. Journal of Machine Learning Research, 2002, 2: 175-211.

[5] Kondor R I, Lafferty J D. Diffusion kernels on graphs and other discrete input structures[C]//Proceedings of the 19th International Conference on Machine Learning. San Francisco, USA: Morgan Kaufmann Publishers Inc, 2002: 315-322.

[6] Roth V, Laub J, Kawanabe M, et al. Optimal cluster preserving embedding of nonmetric proximity data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1540-1551.

[7] Lin H T. Lin C J.Astudy on sigmoid kernels for SVM and the training of non-PSD kernels by SMO-type methods[EB/OL]. (2003)[2015-03-30]. http://www.csie.ntu.edu.tw/～htlin/paper/ doc/tanh.pdf.

[8] Haasdonk B. Feature space interpretation of SVMs with indefinite kernels[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(4): 482-492.

[9] Loosli G, Ong C S, Canu S. SVM in Krein spaces[R/OL]. (2013)[2015-03-30]. https://hal.archives-ouvertes.fr/hal-00869658/document.

[10] Alabdulmohsin I, Gao Xin, Zhang Xiangliang. Support vector machines with indefinite kernels[C]//Proceedings of the 6th Asian Conference on Machine Learning, Vietnam, 2014: 32-47.

[11] Grotschel M, Wakabayashi Y. A cutting plane algorithm fora clustering problem[J]. Mathematical Programming, 1989, 45(1/3): 59-96.

[12] Luss R, d'Aspremont A. Support vector machine classification with indefinite kernels[C]//Advances in Neural Information Processing Systems 21: Proceedings of the 22nd Annual Conference on Neural Information Processing Systems, Vancouver, Canada, Dec 8-11, 2008: 953-960.

[13] Chen Jianhui, Ye Jieping. Training SVM with indefinite kernels[C]//Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 2008. New York, USA:ACM, 2008: 136-143.

[14] Chen Yihua, Gupta M R, Recht B. Learning kernels from indefinite similarities[C]//Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, Canada, 2009. New York, USA:ACM, 2009: 145-152.

[15] Gu Suicheng, Guo Yuhong. Learning SVM classifiers with indefinite kernels[C]//Proceedings of the 26th AAAI Conference on Artificial Intelligence. Menlo Park, USA: AAAI, 2012.

[16] Xu Linli, Neufeld J, Larson B, et al. Maximum margin clustering[C]//Advances in Neural Information Processing Systems 17: Proceedings of the 18th Annual Conference on Neural Information Processing Systems, Vancouver, Canada, Dec 13-18, 2004: 1537-1544.

[17] Zhang Kai, Tsang I W, Kwok J T. Maximum margin clustering made practical[J]. IEEE Transactions on Neural Networks, 2009, 20(4): 583-596.

[18] Yuille A L, Rangarajan A. The concave-convex procedure (CCCP)[J]. Neural Computation, 2003, 15(4): 915-936.

[19] Zhao Bin, Kwok J T, Zhang Changshui. Multiple kernel clustering[C]//Proceedings of the SIAM International Conference on Data Mining, Sparks, USA, Apr 30-May 2, 2009. Philadelphia, USA: SIAM, 2009: 638-649.

[20] Wang Fei, Zhao Bin, Zhang Changshui. Linear time maximum margin clustering[J]. IEEE Transactions on Neural Networks, 2010, 21(2): 319-332.

[21] Zhang Xiaolei, Wu Ji. Linearithmic time sparse and convex maximum margin clustering[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part B Cybernetics, 2012, 42(6): 1669-1692.

[22] Li Yufeng, Tsang I W, Kwok J T, et al. Tighter and convex maximum margin clustering[J]. Journal of Machine Learning Research, 2009, 5: 344-351.

[23] Wu Ji, Zhang Xiaolei. Sparse kernel maximum margin clustering[J]. Neural Network World, 2011, 21(6): 551.

[24] Gopalan R, Sankaranarayanan J. Max-margin clustering: detecting margins from projections of points on lines[C]// Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, Jun 20-25, 2011. Piscataway, USA: IEEE, 2011: 2769-2776.

[25] Zhao Bin, Wang Fei, Zhang Changshui. Efficient maximum margin clustering via cutting plane algorithm[C]//Proceedings of the SIAM International Conference on Data Mining, Atlanta, USA, Apr 24-26, 2008. Philadelphia, USA: SIAM, 2008: 751-762.

[26] Hettich R, Kortanek K O. Semi-infinite programming: theory, method,andapplications[J].SIAMReview,1993,35(3):380-429.

[27] Asuncion A, Newman D. UCI machine learning repository. 2007.

[28] Rakotomamonjy A, Bach F, Canu S, et al. SimpleMKL[J]. Journal of Machine Learning Research, 2008, 9: 2491-2521.

LI Sen was born in 1989. He is an M.S. candidate at School of Computer Science and Engineering, Southeast University. His research interests include machine learning and pattern recognition, etc.

李森（1989—），男，东南大学计算机科学与工程学院硕士研究生，主要研究领域为机器学习，模式识别等。

XUE Hui was born in 1979. She received the Ph.D. degree in computer application technology from Nanjing University of Aeronautics and Astronautics in 2008. Now she is an associate professor and M.S. supervisor at School of Computer Science and Engineering, Southeast University, and the member of CCF. Her research interests include machine learning and pattern recognition, etc.

薛晖（1979—），女，江苏南京人，2008年于南京航空航天大学计算机应用专业获得博士学位，现为东南大学计算机科学与工程学院副教授、硕士生导师，CCF会员，主要研究领域为机器学习，模式识别等。

Indefinite Kernel Maximum Margin Clustering Algorithm*

LI Sen1,2, XUE Hui1,2+
1. School of Computer Science and Engineering, Southeast University, Nanjing 211189, China
2. Key Laboratory of Computer Network and Information Integration, Ministry of Education, Southeast University, Nanjing 211189, China
+ Corresponding author: E-mail: hxue@seu.edu.cn

LI Sen, XUE Hui. Indefinite kernel maximum margin clustering algorithm. Journal of Frontiers of Computer Science and Technology, 2016, 10(1)：112-121.

Abstract:Limited to traditional statistical learning theory, most kernel methods require the kernel matrices to be positive semi-definite. But in many practical problems, such requirement is difficult to be satisfied and thus indefinite kernels appear. Recently, researchers have proposed many methods to solve indefinite kernel classification problems and achieved much better performance. However, the research about indefinite kernel clustering is relatively scarce. Furthermore, existing clustering methods are mainly designed based on positive definite kernels which are incapable in indefinite kernel scenarios. This paper proposes a novel method termed as indefinite kernel maximum margin clustering (IKMMC) based on the state-of-the-art maximum margin clustering (MMC) model. IKMMC aims to find a proxy positive definite kernel to approximate the original indefinite one and thus embeds a new F-norm regularizer measuring the diversity of the two kernels into the MMC model. Given a set of initial labels, IKMMC uses an iterative approach to optimize the objective function and takes the error rate of prediction as the loop-termination criteria. At each iteration, IKMMC transfers the objective function into semi-infinite program (SIP) form, and dynamically adjusts constraint set for optimizing alternately.The experimental results show the superiority of IKMMC algorithm.

文献标志码：A

中图分类号：TP391.4

doi:10.3778/j.issn.1673-9418.1505052