融合互近邻降噪的动态数据流分类研究*

刘三民，王忠群，刘　涛，修　宇.安徽工程大学计算机与信息学院，安徽芜湖4000.安徽工程大学管理工程学院，安徽芜湖4000



融合互近邻降噪的动态数据流分类研究*

刘三民1+，王忠群2，刘涛1，修宇1
1.安徽工程大学计算机与信息学院，安徽芜湖241000
2.安徽工程大学管理工程学院，安徽芜湖241000

* The National Natural Science Foundation of China under Grant Nos. 61300170, 71371012 (国家自然科学基金); the Key Project for Outstanding Young Talents in Higher Education Institutions of Anhui Province under Grant No. 2013SQRL034ZD (安徽省高校优秀人才重点项目); the General Project in Education Department of Anhui Province under Grant No. TSKJ2014B10 (安徽省教育厅一般项目); the Natural Science Foundation of Anhui Province under Grant No. 1608085MF147 (安徽省自然科学基金).

Received 2015-04,Accepted 2015-07.

CNKI网络优先出版：2015-08-11, http://www.cnki.net/kcms/detail/11.5602.TP.20150811.1522.006.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0036-07

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

摘要：动态数据流分类挖掘应用场景逐渐增多，如何辨识出动态数据流中概念漂移和噪声信息成为数据流分类研究中的重点。因此提出一种具备噪声检测能力的动态数据流增量式分类挖掘模型解决此类问题。当动态数据流中出现样本信息与分类模型概念不相容时，采用互近邻思想检测样本是否为噪声，在此基础上用支持向量机作为学习器，通过增量式学习解决数据流中概念漂移。在两种不相容度量标准下，结合理论分析和实验，证明了所提的分类方案是有效可行的。

关键词：互近邻；增量学习；数据流分类；不确定性；概念漂移

1　引言

物联网、云计算、Web2.0等新兴技术的快速发展和应用需求的推动，数据不断自主产生并以流的形式呈现，使得数据流分类成为亟待解决的问题[1]。由于数据产生过程出现概念漂移，导致静态数据挖掘模型无法满足动态数据流环境中的分类需求[2-3]。同时由于设备或环境的影响，数据流中不可避免存在噪声，影响分类挖掘模型的有效性，增加动态数据流分类的复杂性。

针对动态数据流分类问题，国内外学者进行了大量研究，并取得进展。在概念漂移检测方面，文献[4]把数据块映射成概念向量进行聚类，通过计算数据集与对应概念向量之间的距离来判断概念变化。文献[5]根据中心极限定理实现概念漂移检测模型，该模型不依赖于数据分布等先验信息，具有一定实践意义。为提高分类模型的准确性，朱群等人[6]提出一种双层窗口机制数据流分类方法，解决单窗口机制难以适应多种类型概念漂移问题，同时抗噪性能显著提高。文献[7]结合集成学习和增量学习方法，解决数据流分类问题，实验显示该方法具有较高的准确率。文献[8]融合水平集成和垂直集成分别解决噪声和概念漂移问题，实验结果证明方法可行，不足之处是集成规模难以控制。文献[9]针对数据流分类中出现概念漂移和类不平衡问题，提出一种在线神经网络集成方法，其难点在于众多的实验参数如何优化。文献[10]从事前和事后两种角度分析概念漂移发生特点，提出一种分类挖掘框架。文献[11]根据聚类思想，实现一种自适应集成方法解决数据流分类问题。在动态数据流分类时集成式解决方案有其优势，但仍存在某些关键问题需妥善解决，如子分类器的更新、权重计算和结果融合等。增量式学习方法能够解决概念漂移问题，但易受噪声影响，无法有效分辨数据流中的概念漂移样本和噪声信息。

针对上述问题，本文提出了一种融合噪声检测的增量式动态数据流分类处理方案。该方案未采用先概念漂移检测后更新训练学习模型的传统思路，而是针对当前不相容的样本进行噪声检测来判断样本是否适合作为增量学习样本。该方案的优势在于，避免通过数理统计推断的方法来检测概念漂移时因噪声样本的影响而降低准确性。

2　动态数据流中噪声检测

2.1基本概念

为便于描述，首先给出本文所用到的两个基本概念：

定义1（数据流）形如{…，(xi−1，yi−1)，(xi，yi)，(xi＋1，yi＋1)，…}，其中xi表示特征属性信息，yi表示对应类别信息。

基于数据流概念可以描述动态数据流中概念漂移现象。

定义2（概念漂移）是指在相邻时间段内，数据产生的联合概率分布函数不一致现象，即pt(x，y)≠pt＋1(x，y)。

由上述定义可知，一旦数据流中产生概念漂移现象，基于历史样本获得的分类模型在概念表示上将与新样本不相容，这种不相容现象表现为对新样本类别预测错误，或者是对新样本的类别信息预测具有较大的不确定性。噪声样本在外部表现上与新概念样本相似，因此在具有噪声的动态数据流分类时应该对噪声样本与新概念样本进行甄别。

2.2基于互近邻的噪声检测

根据聚类思想可知相邻样本具有较高的相似性，即两者之间概念相似的概率非常大。基于此观点本文提出了互近邻的噪声消除方法，基本思想是当样本与互近邻集合中样本概念多数不一致时，即判断为噪声。

设样本集S＝{(xi，yi)，i＝1，2，…，n}，其中xi是由特征属性构成的矢量，yi代表类别信息。在此样本集上，可以给出相应概念的描述。

定义3（k-近邻）指样本xi在集合S中距离最近的k个样本集合，本文记为Nk(xi)。

基于k-近邻思想广泛应用于分类和聚类学习中，实现过程中由于样本过分依赖于近邻信息来确定自己的类别情况，可能会出现误判断现象，即伪近邻效应，也就是样本的近邻并没有把该样本作为它的近邻。为避免伪近邻现象导致的误判断，本文引出互近邻的概念解决相应问题。互近邻概念强调信息的对称性，即真正近邻是互相承认的近邻关系。

定义4（k-互近邻）若样本xi∈Nk(xj)，且同时xj∈Nk(xi)成立，则称样本xi、xj为k-互近邻。

根据定义4可知在样本集合S中，样本x的k-互近邻集合可记为Mk(x)＝{xi∈S|xi∈Nk(x)∩x∈Nk(xi)}。结合k-近邻和k-互近邻的定义归纳出两条有用的性质，这是本文基于互近邻进行噪声检测的基础。

性质1给定样本集，样本x的k-互近邻是k-近邻的子集，即Mk(x)⊆Nk(x)。

证明根据k-互近邻的定义形式化Mk(x)＝{xi∈S| xi∈Nk(x)∩x∈Nk(xi)}可直接证明性质1是成立的。□

性质1保证通过求样本的近邻信息来获得互近邻信息是完备的。

性质2给定近邻k的参数值，样本x与其互近邻集合中的所有样本必然满足互为k-近邻的近邻关系。

证明设样本xi∈Mk(x)，由定义2可知xi∈Nk(x) 与x∈Nk(xi)是同时成立的。又由样本xi的任意性可知性质2是成立的。□

性质2保证所求近邻信息是真正近邻，提高基于互近邻进行噪声检测的可靠性。

根据上述分析，本文的噪声检测算法（noisy elimination algorithm，NEA）描述如下所示。

算法1 NEA

输入：S表示样本集，x为待测样本，k表示近邻数。

输出：待测样本是否为噪声信息。

1.求样本x的k-近邻，遍历k-近邻中每个样本求其k-近邻，凡满足{xi∈S|xi∈Nk(x)∩x∈Nk(xi)}的样本并入Mk(x)中。

2. If Mk(x)＝ϕ返回样本x是噪声。

3. else统计Mk(x)中与样本x类别相同的互近邻个数count值

4. If count＜Mk(x)/2，返回样本x是噪声。

3　具有噪声消除的动态数据流增量式分类

鉴于集成学习尚存在某些问题需要解决，本文采用增量式学习来适应数据流概念的动态变化。由于支持向量机具备出色的泛化性能而备受青睐，而且通过支持向量集进行样本数量归约，能够降低增量学习时样本复杂性，因此本文采用支持向量机算法作为增量学习器。

3.1支持向量机

支持向量机的实现本质是求解能够正确划分样本集的最优分类超平面，当在原样本空间线性不可分时，通过核映射把线性不可分问题转化至高维空间实现线性可分，而且无需掌握映射函数信息。最优超平面求解可以通过如下最优化问题求解：

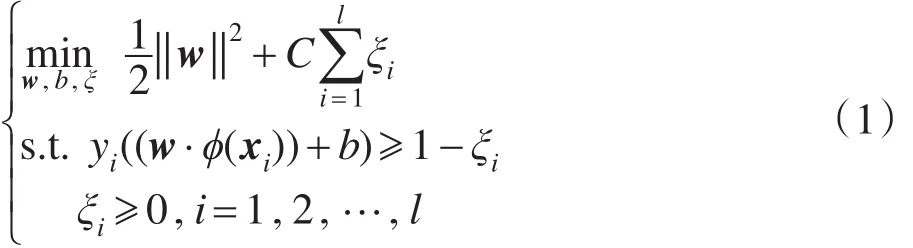
其中，C是惩罚因子，表示对错分样本的关注程度；ξi表示样本松弛变量。根据拉格郎日最优化方法，上式可转化成下式易于求解的最优化问题：

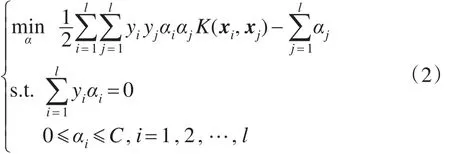
其中，K(xi，xj)为核函数。通过最优化求解可得相应的分类函数：

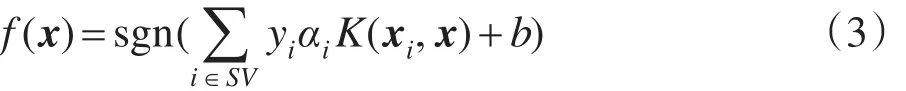
在分类函数中，αi是拉格朗日乘子。由式（3）可知，最优分类面是由乘子αi非零样本构成，这些样本称为支持向量（support vector，SV）。

3.2增量式数据流分类模型

在动态数据流分类中，增量式学习关键是从数据流中选出代表概念变化的样本进行更新学习。由前文可知，当数据流出现概念漂移时，分类器具有较高概率错分样本或者分类结果呈现较大的不确定性，即此时出现分类器知识与样本概念不相容现象。因此本文后续研究将在两种概念不相容的度量基础上进行分析。

文献[12]对样本不确定性进行详细的分析，本文将采用相同的样本不确定性概念，即样本不确定性是指基于当前分类器关于样本类别随机变量的后验概率信息熵的大小。本文仅讨论两分类问题，故样本不确定性计算公式如下：

其中，pi表示样本属于第i类的后验概率。

综上可得动态数据流增量式学习分类流程，如图1所示。

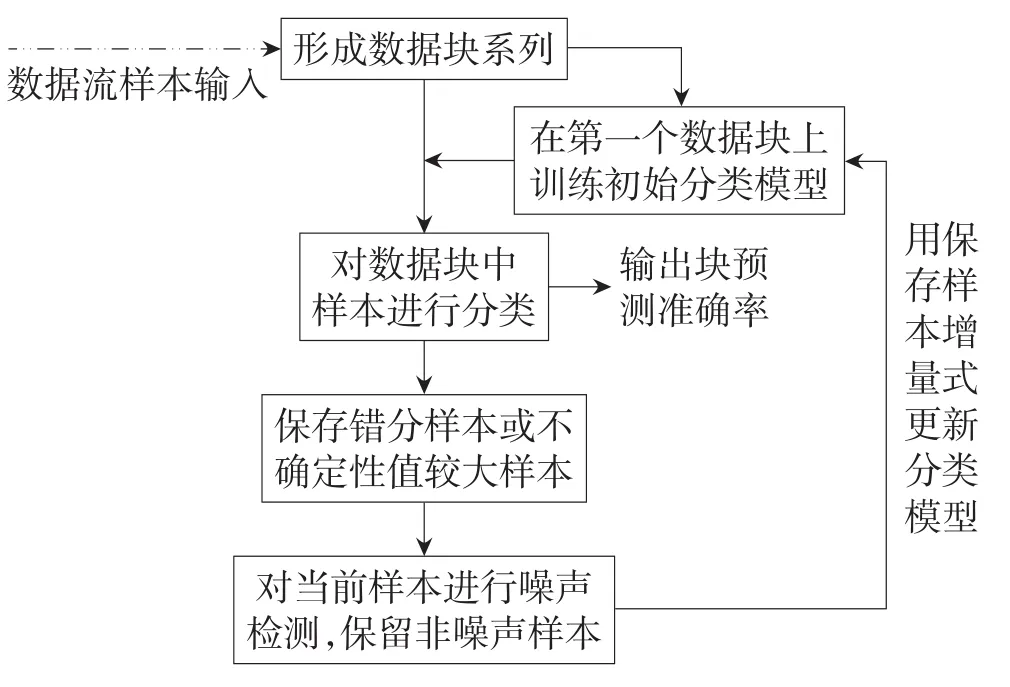
Fig.1 Flowchart of incremental learning图1　增量式学习流程

基于图1可以给出基于样本不确定性的噪声消除增量式数据流分类算法，文中记为SUNEIL（sample uncertainty based noisy elimination incremental learning algorithm）。

算法2 SUNEIL

输入：DS＝{…，DBt−1，DBt，DBt＋1，…}，其中DBt表示固定大小的数据块；支持向量机学习算法L；不确定性阈值θ；增量集IDS。

输出：分类模型φ。

1.训练初始分类模型(φ，sv)＝L(DB1)，其中sv表示支持向量

2. For i＝2 to|DS |

3.For j＝1 to|DBi|

4.用分类模型φ预测数据块中样本sj的后验概率，并根据式（4）求不确定性值u

5.If (u＞θ)成立，则调用噪声检测算法NEA (DBi，sj，k)

6.如果样本sj为非噪声，则IDS＝IDS∪sj

7. (φ，sv)＝L(IDS∪sv)

类似可得基于错误样本的增量式学习算法，文中记为ESNEIL（error sample based noisy elimination incremental learning algorithm）。

算法3 ESNEIL

输入：DS＝{…，DBt−1，DBt，DBt＋1，…}，其中DBt表示固定大小的数据块；支持向量机学习算法L；增量集IDS。

输出：分类模型φ。

1.训练初始分类模型(φ，sv)＝L(DB1)，其中sv表示支持向量

2. For i＝2 to|DS |

3.For j＝1 to|DBi|

4.用分类模型φ预测数据块中样本sj的类别，当预测错误时调用噪声检测算法NEA (DBi，sj，k)

5.如果样本sj为非噪声，则有IDS＝IDS∪sj

6.(φ，sv)＝L(IDS∪sv)

4　仿真实验及结果分析

仿真数据流源于大型在线仿真平台MOA[13]中的移动超平面数据流，在3种不同噪声比率的数据流环境进行实验，对比3种实验方案，即基于不确定性增量式数据流分类（sample uncertainty based incremental learning algorithm，SUIL）、基于不确定性的噪声消除增量式数据流分类（SUNEIL）和基于错分样本的噪声消除增量式数据流分类（ESNEIL）。

4.1移动超平面数据流

移动超平面数据流[14]仿真生成办法可以表示成m维超平面，其中特征值xi在区间（0，1）上随机生成。当满足时，由各特征值构成的样本(x1，x2，…，xm)代表正类样本，否则为负类样本，即，其中。在MOA平台上通过调节参数生成不同的实验数据集：噪声参数n用来随机改变样本类别的概率大小，表示数据集中噪声比；幅度调节参数m表示权值的变化量大小；参数s∈{−1，1}表示a方向改变情况，即按照设置的概率把s变成−s。研究目标是解决噪声环境下动态数据流分类问题，因此生成3组实验数据集(H1，H2，H3)，每个实验数据集包含20 000条样本信息，每个样本由5个特征属性构成，其中2个特征属性发生漂移，参数m取值0.1，参数s为10%。为分析基于互近邻的噪声检测性能，分别往3个数据集H1、H2、H3中加入类噪声25%、30%、35%。

4.2实验结果分析

实验环境基于Matlab7.1平台，结合LibSVM[15]软件包完成，实验时支持向量机相关参数均按缺省值设置。结合文献[12]，本文的近邻参数k值和样本不确定性阈值依据经验设置，分别为3和0.66。数据流按照固定数据块大小（400）进行批量处理，采用先测试后增量更新分类模型的方法，通过记录准确率反映各种方案在噪声环境中的动态数据流分类性能。图2～图4分别表示不同的噪声数据流中3种实验方案的变化曲线。

Fig.2 Accuracy of data block with 25% noisy图2　含25%噪声的数据块准确率

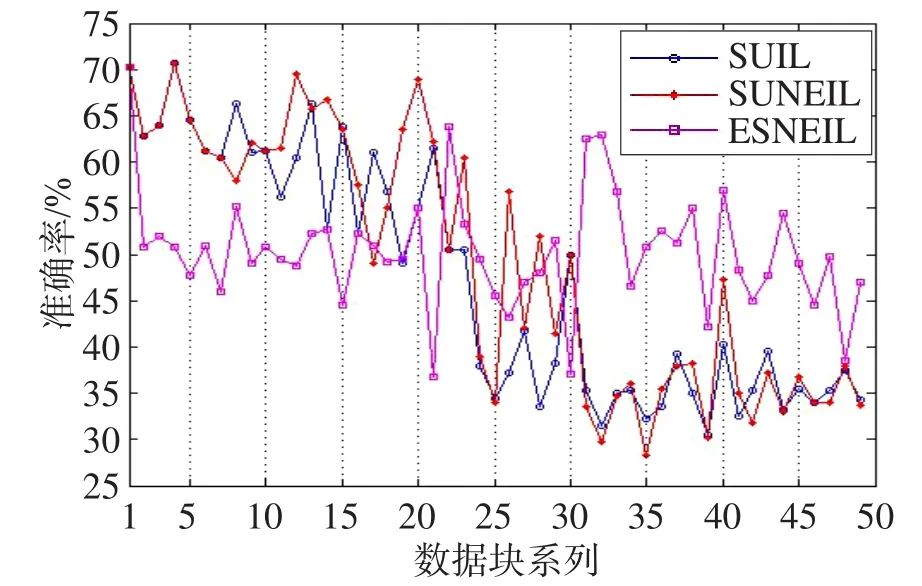
Fig.3 Accuracy of data block with 30% noisy图3　含30%噪声的数据块准确率

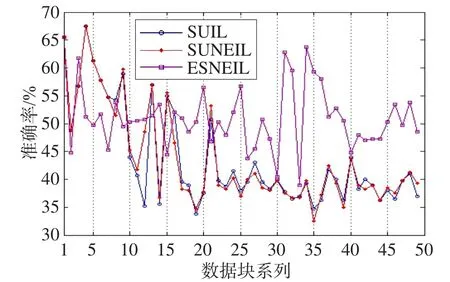
Fig.4 Accuracy of data block with 35% noisy图4　含35%噪声的数据块准确率

由图2～图4中的准确率变化曲线可知，本文的分类方案是可行的。通过互近邻办法能够发现动态数据流环境中的噪声信息，利用增量式学习解决概念漂移问题。通过对比实验曲线可知，仅依赖于样本不确性进行增量学习（SUIL）随着噪声比例增加，准确性将急剧下降。而且在3种噪声环境中，随着数据块的不断处理，准确率曲线呈下降趋势明显，这是由于噪声数据被认为是概念漂移样本加入增量学习当中，导致学习器概念无法收敛。对比融入互近邻的噪声消除增量式学习方法可知，进行噪声检测在一定程度上缓解了噪声样本的影响，准确率曲线变化相对较为平缓，且平均值也高于SUIL分类方案。通过上述3个图形准确率曲线可知，基于错分样本的噪声消除增量学习方案（ESNEIL）较好。特别是当噪声增加时，随着数据块处理ESNEIL的准确性很快就优于其他两种方案，且越来越明显。通过实验观察发现，ESNEIL在整个处理过程中，效率较高，支持样本数量明显偏少，是另外两种方案的一半左右。这说明在具备噪声的动态数据流分类过程中，在表征分类器与样本概念不相容时用错分样本较好，在此基础上再进行噪声检测是较优的处理方案。

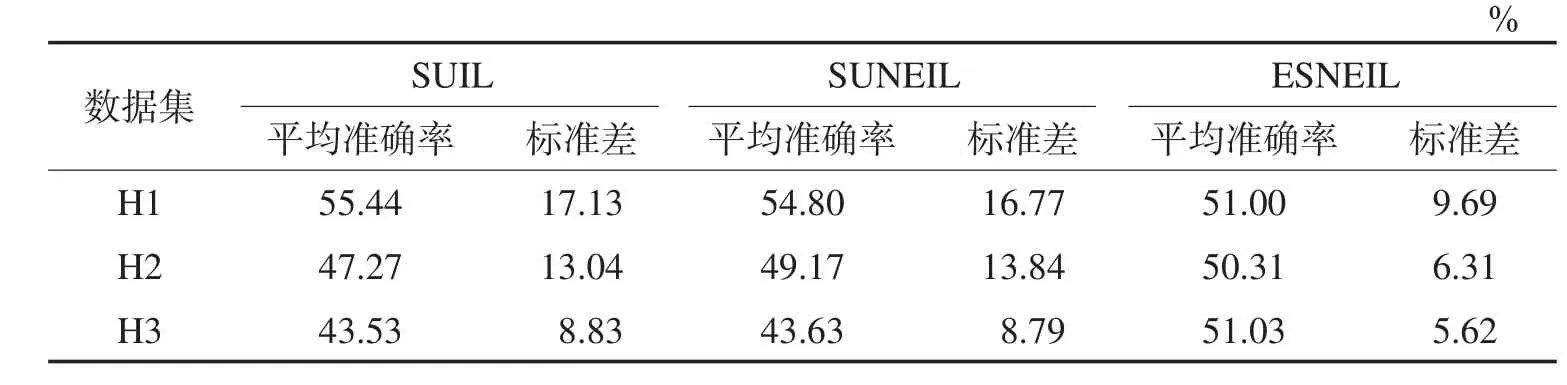
Table 1 Mean and standard deviation of accuracy表1　准确率的平均值和标准差

表4中的统计量值也再次证实了上述相关结论，在3种噪声环境下，ESNEIL的标准差是最小的，而且平均准确率相比也是最好的。采用增加了互近邻的噪声消除方法后，SUNEIL和ESNEIL准确率在相同的情况下均比SUIL要好，而且标准差值要小。这说明噪声消除能够辨识出概念变化样本和噪声样本，特别是当噪声增加时，其相关准确性和健壮性均能得到显著提升。

5　结束语

针对噪声环境中动态数据流分类问题，本文提出了一种噪声消除的增量式学习方案。通过实验数据证明了所设计的方案能够解决所提出的问题，而且通过相关性质说明了噪声消除方案是可靠的。在研究过程中发现，基于错分样本的增量式学习方案支持向量集规模增长较为平缓，而基于样本不确定性的增量式学习方案面临支持向量集规模增大的困境，影响分类效率。后续研究将在概念倾斜的框架上，通过双惩罚因子的支持向量机解决此问题。

References:

[1] Sun Dawei, Zhang Guangyan, Zheng Weimin. Big data stream computing: technologies and instances[J]. Journal of Software, 2014, 25(4): 839-862.

[2] Zliobaite I. Learning under concept drift: an overview[R]. Vilnius, Lithuania: Faculty of Mathematics and Informatics, Vilnius University, 2009.

[3] He Qing, Li Ning, Luo Wenjuan, et al. A survey of machine learning algorithms for big data[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(4): 327-336.

[4] Katakis I, Tsoumakas G, Vlahavas I. Tracking recurring contexts using ensemble classifiers: an application to email filtering[J]. Knowledge and Information Systems, 2010, 22(3): 371-391.

[5] Alippi C, Boracchi G, Roveri M. An effective just-in-time adaptive classifier for gradual concept drifts[C]//Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, USA, Jul 31-Aug 5, 2011. Piscataway, USA: IEEE, 2011: 1675-1681.

[6] Zhu Qun, Zhang Yuhong, Hu Xuegang, etal.Adouble-windowbased classification algorithm for concept drifting data streams[J].Acta Automatica Sinica, 2011, 37(9): 1078-1083.

[7] Flwell R, Polikar R. Incremental learning of concept drift in nonstationary environments[J]. IEEE Transactions on Neural Networks, 2011, 22(10): 1517-1531.

[8] Zhang Peng, Zhu Xingquan, Shi Yong, et al. Robust ensemble learning for mining noisy data streams[J]. Decision Support Systems, 2011, 50(2): 469-479.

[9] Ghazikhani A, Monsefi R, Yazdi H S. Ensemble of online neural networks for nonstationary and imbalanced data streams[J]. Neurocomputing, 2013, 122: 535-544.

[10] Hofer V, Georg K. Drift mining in data: a framework for addressing drift in classification[J]. Computational Statistics and Data Analysis, 2013, 57(1): 377-391.

[11] Dewan M F, Zhang Li, Alamgir H, et al. An adaptive ensemble classifier for mining concept drifting data streams[J]. Expert Systems with Applications, 2013, 40(15): 5895-5906.

[12] Liu Sanmin, Sun Zhixin, Liu Tao. Research of incremental data stream classification based on sample uncertainty[J]. Journal of Chinese Computer Systems, 2015, 36(2): 193-196.

[13] Holmes G, Kirkby R, Pfahringer B. MOA: massive onlineanalysis[EB/OL]. (2010)[2015-03-09]. http://sourceforge.net/ projects/moa-datastream.

[14] Hulten G, Spencer L, Domingos P. Mining time changing data streams[C]//Proceedings of the 2001 ACM International Conference on Knowledge Discovery and Data Mining, San Francisco, USA, 2001. New York, USA: ACM, 2001: 97-106.

[15] Chang C C, Lin C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 27(2): 1-27.

附中文参考文献：

[1]孙大为,张广艳,郑纬民.大数据流式计算:关键技术及系统实例[J].软件学报, 2014, 25(4): 839-862.

[3]何清,李宁,罗文娟,等.大数据下的机器学习算法综述[J].模式识别与人工智能, 2014, 27(4): 327-336.

[6]朱群,张玉红,胡学钢,等.一种基于双层窗口的概念漂移数据流分类算法[J].自动化学报, 2011, 37(9): 1077-1084.

[12]刘三民,孙知信,刘涛.基于样本不确定性的增量式数据流分类研究[J].小型微型计算机系统, 2015, 36(2): 193-196.

LIU Sanmin was born in 1978. He is an associated professor and Ph.D. at Anhui Polytechnic University. His research interests include pattern recognition, machine learning and data mining, etc.

刘三民（1978—），男，安徽安庆人，安徽工程大学副教授、博士，主要研究领域为模式识别，机器学习，数据挖掘等。

WANG Zhongqun was born in 1965. He is a professor at Anhui Polytechnic University. His research interests include software engineering, information management and information system, etc.

王忠群（1965—），男，安徽芜湖人，安徽工程大学教授，主要研究领域为软件工程，信息管理与信息系统等。

LIU Tao was born in 1973. She is an associated professor at Anhui Polytechnic University. Her research interests include network and information security, etc.

刘涛（1973—），女，安徽六安人，安徽工程大学副教授，主要研究领域为网络与信息安全等。

XIU Yu was born in 1976. He is a lecturer at Anhui Polytechnic University. His research interests include data mining and machine learning, etc.

修宇（1976—），男，山东单县人，安徽工程大学讲师，主要研究领域为数据挖掘，机器学习等。

Research on Dynamic Data Streams Classification with Noise Elimination Using Mutual Nearest Neighbor*

LIU Sanmin1+, WANG Zhongqun2, LIU Tao1, XIU Yu1
1. College of Computer and Information,Anhui Polytechnic University, Wuhu,Anhui 241000, China
2. College of Management Engineering,Anhui Polytechnic University, Wuhu,Anhui 241000, China
+ Corresponding author: E-mail: aqlsm@163.com

LIU Sanmin, WANG Zhongqun, LIU Tao, et al. Research on dynamic data streams classification with noise elimination using mutual nearest neighbor. Journal of Frontiers of Computer Science and Technology, 2016, 10(1)：36-42.

Abstract:Application scenarios of dynamic data streams classification are increasing, and it is very important to discriminate concept drift from noisy information in data streams classification. This paper proposes an incremental classification model with noisy elimination for dynamic data streams classification to solve this problem. When dynamic data streams sample is incompatible with the concept of classifier model, the mutual nearest neighbor is used to detect noisy sample. Based on it, support vector machine is used as learner, and then concept drift in data streams is solved by incremental learning. Under two different metrics about incompatibility, classification schema is effective through the theory analysis and simulation experiment.

Key words:mutual nearest neighbor; incremental learning; data streams classification; uncertainty; concept drift

文献标志码：A

中图分类号：TP311

doi:10.3778/j.issn.1673-9418.1504009