基于ILS-CS优化算法的个性化旅游线路研究*

侯　乐，杨辉华,2+，樊永显，李灵巧,2，蒋淑洁.桂林电子科技大学电子工程与自动化学院，广西桂林540042.北京邮电大学自动化学院，北京00876.桂林电子科技大学计算机科学与工程学院，广西桂林54004

* The National Natural Science Foundation of China under Grant Nos. 21365008, 61105004 , 61462018 (国家自然科学基金); the Natural Science Foundation of Guangxi under Grant No. 2012GXNSFAA053230 (广西自然科学基金); the Scientific Research Fund of Guangxi Education Department under Grant No. LX2014139 (广西教育厅科研项目); the Innovation Project of Graduate Education of Guilin University of Electronic Technology under Grant No. GDYCSZ201478 (桂林电子科技大学研究生教育创新计划资助项目).

Received 2015-03,Accepted 2015-06.

CNKI网络优先出版：2015-06-05, http://www.cnki.net/kcms/detail/11.5602.TP.20150605.1537.002.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0142-09



基于ILS-CS优化算法的个性化旅游线路研究*

侯乐1，杨辉华1,2+，樊永显3，李灵巧1,2，蒋淑洁1
1.桂林电子科技大学电子工程与自动化学院，广西桂林541004
2.北京邮电大学自动化学院，北京100876
3.桂林电子科技大学计算机科学与工程学院，广西桂林541004

* The National Natural Science Foundation of China under Grant Nos. 21365008, 61105004 , 61462018 (国家自然科学基金); the Natural Science Foundation of Guangxi under Grant No. 2012GXNSFAA053230 (广西自然科学基金); the Scientific Research Fund of Guangxi Education Department under Grant No. LX2014139 (广西教育厅科研项目); the Innovation Project of Graduate Education of Guilin University of Electronic Technology under Grant No. GDYCSZ201478 (桂林电子科技大学研究生教育创新计划资助项目).

Received 2015-03,Accepted 2015-06.

CNKI网络优先出版：2015-06-05, http://www.cnki.net/kcms/detail/11.5602.TP.20150605.1537.002.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(01)-0142-09

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

摘要：针对迭代局部搜索（iterated local search，ILS）算法求解旅游线路时间花费较长的问题，提出了一种ILS结合布谷鸟搜索（cuckoo search，CS）的优化算法，来优化旅游线路的时间花费。该算法首先根据相关目标和约束采用ILS算法求解旅游景点及初始旅游线路，然后在满足旅游景点时间窗约束及景点总数不变的情况下采用CS算法进一步最小化旅游线路的时间花费。该研究获得的线路更符合旅游习惯，并且旅游时间花费更少。通过Daminaos数据集和桂林景点数据集进行验证，结果表明该优化算法相比于仅使用ILS算法所规划出的旅游线路，平均时间花费减少8%，更符合用户旅游选择习惯。

关键词：旅游线路规划；迭代局部搜索；布谷鸟搜索；带时间窗的定向问题；带时间窗的旅行商问题

1　引言

随着经济社会的发展，旅游业竞争也越来越激烈，如何减少路线安排的盲目性和随意性，为客户提供个性化旅游线路，从而提供更多可供用户选择的旅游方案已逐步成为目前相关企业以及学科的研究热点。然而当前的旅游推荐系统通常通过运筹学方法来寻求最优线路，具有如下问题：（1）未考虑组团旅游的需求；（2）未考虑游客的个性化喜好、需求和约束[1]；（3）未考虑用户选择的开始与结束地点、预算的花费时间以及当前出发的时间。因此需要根据上述约束利用机器学习的方法提出更为合理、更符合用户旅游选择习惯的线路[2]。

最早，针对个性化旅游线路规划问题，Hagen等人[3]通过分支界定法来实现旅游线路的规划，该方法计算时间长，且线路规划不合理。Kramer等人[4]根据每个用户对同一个景点评分的差异性，提出了个性化的旅游线路规划，改善了传统旅游推荐系统通过统计学方法设定单个景点的评分问题。当前，Chao等人将定向问题（orienteering problem，OP）[5]作为个性化旅游线路规划问题的求解优化方案[6-7]。该问题为NP难问题，不能够在多项式时间内求出最优解，且未考虑各景点开放和参观时间。因此Dumas等人针对景点开放时间和参观时间问题，提出了一种带时间窗的旅行商问题（travel salesman problem with time windows，TSPTW）的旅游线路规划。该模型要求所有的景点必须被访问，因此不适用于时间有限、景点数量多的旅游线路规划[8]。近期，Vansteenwegen等人[9]采用迭代局部搜索算法来对带时间窗的定向问题进行求解，该算法能够在较短的时间内计算出一条较优的线路。Gavalas等人[10]采用聚类和迭代搜索相结合的方法解决带时间窗的定向问题。但是上述两种方法规划出来的旅游线路存在行程花费时间较长的缺点。

根据上述研究所存在的问题，本文提出了一种基于迭代局部搜索（iterated local search，ILS）结合布谷鸟搜索（cuckoo search，CS）的优化算法模型。该模型首先采用ILS求解出旅游景点及初始旅游线路，然后在满足旅游景点时间窗约束及景点总数不变的情况下，采用CS算法最小化旅游线路的时间花费。该优化算法通过Daminaos数据集和桂林市的部分景点数据集进行验证，对比于单一使用迭代局部搜索算法所规划出的旅游线路，具有更好的优化效果。

2　问题描述

给定一个完全有向图G＝(V，E)，其中V＝{1，2，…，n}是节点集，E＝{(i，j)|i，j∈V}是边集。每个节点i＝1，2，…，n对应一个得分Si、参观时间Ti和一个时间窗[Oi，Ci]。边tij表示从节点i到节点j所需的时间（包括Tj）。因此，带时间窗的定向问题即找出一条从节点1出发到节点n终止的路径，使得所经过点的总得分最大化。每个节点至多能访问一次，路径中访问相应点所用的总时间不能超过预先规定的时间预算Tmax。若节点j是节点i的下一个访问节点，则xij＝1，反之等于0，xij为决策变量。Tmax满足Tmax＝Cn−O1，带时间窗的定向问题的数学描述为[5]：

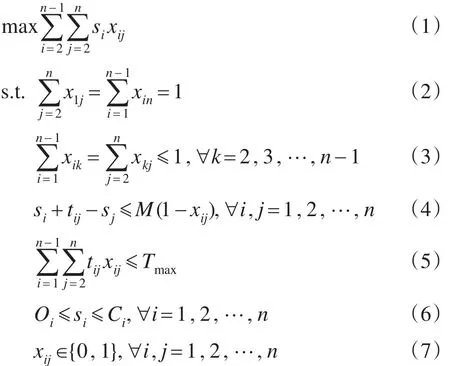
其中，si为访问节点i的开始时间；M为一个大的常量。式（1）为目标函数，表示路径上所有满足xij＝1的点的得分之和最大；式（2）中x1j＝1表示路径必须从节点1出发，xin＝1表示路径中n为最后节点；式（3）中xik和xkj表示每个节点至多被访问一次，不允许节点被重复访问；式（4）表示若节点i、j联通，则j的开始时间等于i的开始时间加上节点i、j的距离和i的参观时间，若节点i、j不联通，则j的开始时间始终大于si和tij之和，确保节点时间的连通性；式（5）表示路径中所有联通节点花费的时间总和（包括节点之间的距离、参观时间及等待时间）小于时间预算Tmax；式（6）表示节点i的访问开始时间大于i的开放时间并小于其关闭时间；式（7）表示xij为决策变量，其值为0或1。

优化算法的核心是将ILS算法规划出的初始旅游线路作为带时间窗的旅行商问题[8]，使用布谷鸟搜索算法[11]对其进行优化。TSPTW问题可描述为：对于给定的一组节点集合{1，2，…，n}，节点1和节点n分别为起始和终止节点，每个节点i有一参观时间Ti和一个时间窗[Oi，Ci]，每个节点只能在其时间窗内被访问。边tij表示从节点i到节点j所需的时间（包括Tj）。优化目标是给出一条访问所有节点的路径，使总的时间花费最少。带时间窗的旅行商问题的数学描述为：

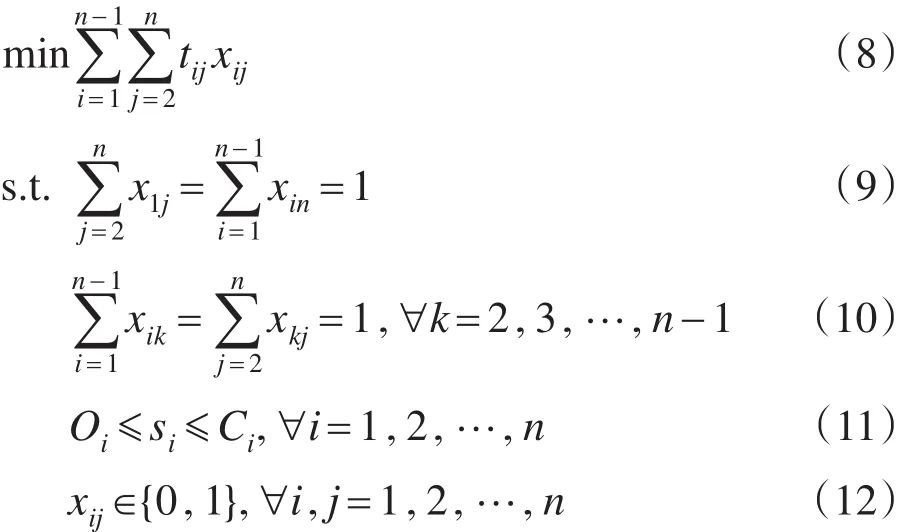
式（8）为目标函数，表示路径中所有联通节点花费时间之和（包括节点之间的距离时间、参观时间及等待时间）最小；式（9）中x1j＝1表示路径必须从节点1出发，xin＝1表示路径中n为最后节点；式（10）中xik和xkj表示每个节点必须访问一次；式（11）表示节点i的访问开始时间大于i的开放时间并小于其关闭时间；式（12）表示xij为决策变量，其值为0或1。

为求解这两个问题，本文采用迭代局部搜索算法和布谷鸟搜索算法依次求解。首先根据相关约束采用迭代局部搜索算法，最大化总收益，求解出旅游景点和初始旅游线路；然后在旅游景点不变的情况下，采用布谷鸟搜索算法进一步优化时间花费。其中，迭代局部搜索算法的基本原理和流程参见文献[9]。

3　优化模型求解

3.1编码方案

本文根据TSPTW问题的特点采用基于优先级的编码方案，每一个编码个体根据优先级的大小表示一种可行解[12]。

以ILS规划出的路径{1，8，3，6，9，2，5，7，4，100}为例，其中1表示出发节点，100表示结束节点，则只需要对其余的8个节点按照优先级编码。具体编码方式如下：

（1）生成8个取值范围为[−2，2]之间的随机数

(−1.230 5，0.345 2，1.735 6，−0.253 6，1.467 3，−0.531 6，0.432 1，0.764 6)

（2）将优先级按照降序排列得到一条编码方案

(1.735 6,1.467 3,0.764 6,0.432 1,0.345 2,−0.253 6，−0.531 6,−1.230 5)则根据上述编码方案解码得到的一条可行解为{1，8，3，6，9，2，5，7，4，100}。

以莱维飞行的方式搜索新的鸟巢并进行位置更新[13]，如式（13）所示：

在CS算法中采用Levy搜索路径，如式（15）所示：

本文取值β＝1.2，u和v服从式（16）的正态分布：

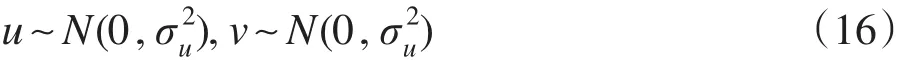
3.2适应度函数

根据基于时间窗的旅行商问题的数学模型，优化目标是该条路径的节点在满足约束的条件下花费时间最少，则CS算法的适应度函数如式（17）所示：

该适应度函数表示对可行解上所有联通的节点计算其总的花费时间，适应度值越小，表示可行解越优，若该可行解上联通节点违反时间窗约束，则该可行解的适应度值设为无限大。

3.3ILS-CS算法流程

ILS-CS算法求解TSPTW问题的流程[14]如下：

（1）定义适应度函数f(x)，计算ILS初始路径的花费时间Tinit；

（2）初始化算法基本参数，布谷鸟选择宿主鸟巢数目n，发现概率pa和最大迭代次数Niter；

（3）布谷鸟随机选择鸟巢位置nesti(i＝1，2，…，n)，按照3.1节的编码方案编码；

（4）根据Levy飞行更新鸟巢位置nesti，计算鸟巢适应度值，保留适应度值最小的鸟巢；

（5）更新鸟巢nesti的位置，得到新的鸟巢位置newNest；

（6）对新鸟巢中的每个个体，宿主以一定的概率pa放弃当前的鸟巢而新建鸟巢，形成新的种群；

（7）再次计算每个鸟巢的适应度f(x)，保留适应度值小于Tinit的可行解；

（8）当达到最大迭代次数则输出最优解，否则转（4）进行下一轮搜索。

4　实验配置及参数设定

4.1数据来源

本文主要使用两种数据：一种数据是来源于百度旅游网桂林市景点的数据集合（http：//lvyou.baidu. co m/guilin/jingdian)，简称Guilin数据集，其中旅游景点的数目为162个，每个节点的Ti在30～480之间。其中开放时间为0～1 440的节点数量86个。另一种是Daminaos[10]数据集（http：//dgavalas.ct.aegean.gr/ public/op_instainst/），其中节点数为n，分布在100～ 200之间，每个节点的参观时间Ti在1到120之间，数据50%的节点开放时间为0～1 440，其余的时间窗为Oi＝510，Ci＝1 020，和各自包含有50个测试样本，两种数据集均为长时间窗。

4.2实验配置

实验环境为一台处理器为Intel®CoreTMi5-2400 CPU，主频为3.1 GHz，内存4 GB的台式机。本文实验所采用的软件为Visual Studio 2012及Sql Server 2008，迭代局部搜索算法来源于Vansteenwegen等人[9]，布谷鸟搜索算法来源于Yang等人[11]。本实验内容包括两组实验分析：

（1）ILS-CS算法优化效果分析；

（2）WebGIS上线路展示效果分析。

4.3gap评价准则

ILS-CS算法优化的目标是在满足时间窗约束的条件下找到一条时间花费更短的线路。本文用时间减少率gap评价优化的效果，gap的求解方式如式（18）所示：

式（18）中，gap表示时间减少率；TILS表示ILS算法规划出线路花费的时间；TCS表示CS对ILS的线路优化后花费的时间；O1表示旅行开始时间。gap值越大表示CS算法的优化效果越好。

5　实验结果及分析

5.1ILS-CS算法优化效果分析

本文采用时间减少率gap以及行程的时间花费作为评价标准来评价基于迭代局部搜索结合布谷鸟搜索的优化算法个性化旅游路线规划的优化效果。

表1中前8条和后4条数据分别是使用Guilin数据集和Daminaos数据集规划出的旅游线路。表中ItineraryILS表示ILS算法规划出的线路；ItineraryCS表示CS算法规划出的线路；TILS表示ILS规划线路花费时间；TCS表示CS优化后花费时间；Cn表示ILS算法规划出的线路旅行结束时间。从表1中可以看出，针对不同的旅游结束时间规划出的旅游线路，优化前后的旅游线路点的个数不变，旅游线路上点的访问顺序发生变化，而优化后的时间花费TILS则比优化前的时间花费TCS有较大的减少，证明了该算法在旅游行程花费时间上优化的有效性。

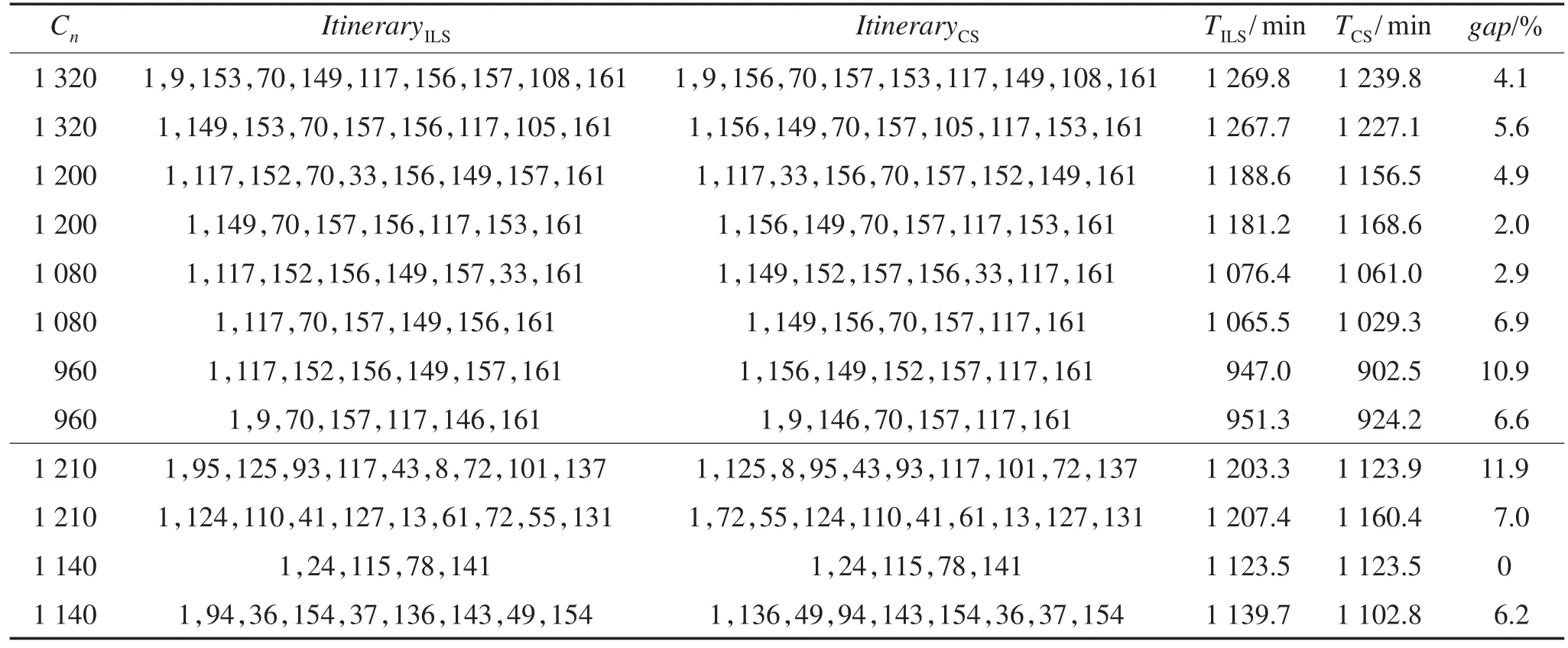
Table 1 Comparison of trip itinerary and spend time表1　优化线路及花费时间对比

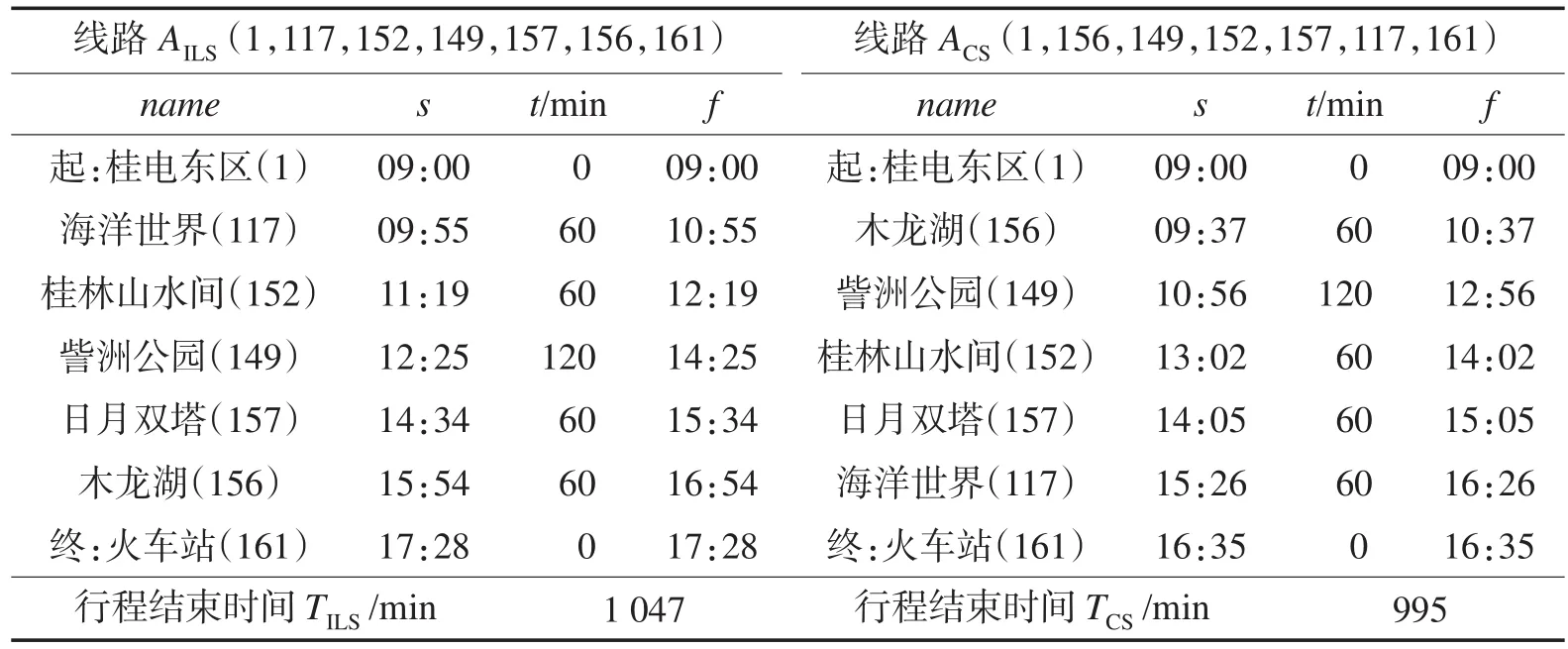
Table 2 Comparison of visit time表2　景点访问时间对比

表2为参数Oi＝540，Ci＝1 080，旅游起点和终点分别为桂林电子科技大学（东校区）和桂林火车站所规划出的一条旅游线路。其中f表示离开景点的时间，s表示开始访问景点时间。表中name一栏括号内的数字表示景点的编号，AILS和ACS分别表示优化前后的线路序列。通过表中可以看出，经过ILS-CS算法优化后，每条旅游线路中景点的访问时间以及旅游线路花费的总时间都发生改变，由式（18）得优化后的时间花费比优化前的时间花费gap减少率达到10.3%。

表3为使用Guilin数据集和Daminaos数据集测试算法优化效果。每个数据集分别测试100条线路样本。其中Guilin数据集的gap值最小为1.2%，最大为12.6%，方差为0.001 48，说明ILS-CS优化算法优化的效果比较稳定。对Daminaos数据集，gap值最小为0（一种情况该算法旅游时间上已经达到最优；另外一种情况是选择出来的景点的时间窗比较短，导致景点旅游顺序的改变，违反景点的时间窗约束，因此无法进一步优化）。

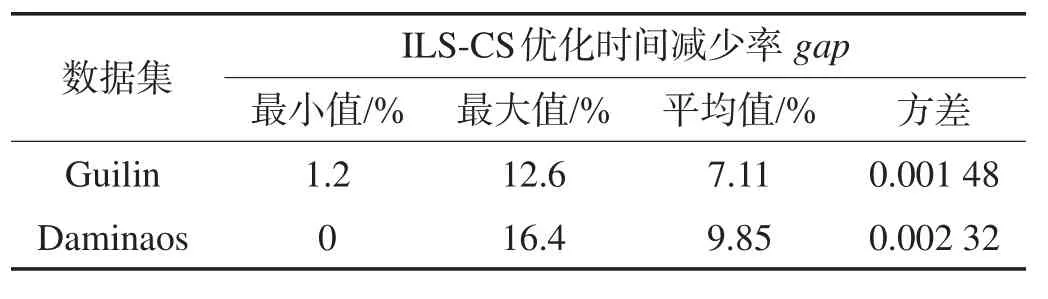
Table 3 Comparison of optimization gap between two data sets表3　两种数据集的优化结果对比

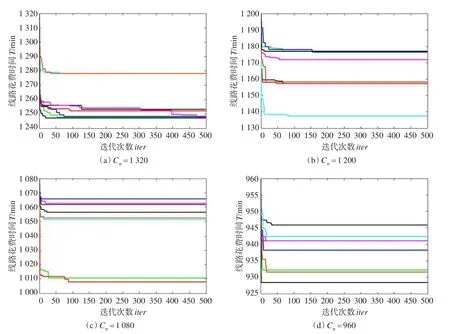
Fig.1 Convergence curves for different Cn图1　不同Cn值的收敛曲线

以下对ILS-CS算法优化的收敛性进行分析，图1为采用ILS算法O1＝540，Cn参数分别为1 320、1 200、1 080、960，随机规划出的8条初始线路使用CS算法优化的收敛曲线图，图中每种颜色代表一条旅游线路。CS参数为n＝10，pa＝0.25，评价次数为5 000。从图中可以得出，对不同的时间约束Cn规划出的线路，ILS-CS优化算法能够快速收敛并得到最优的结果。

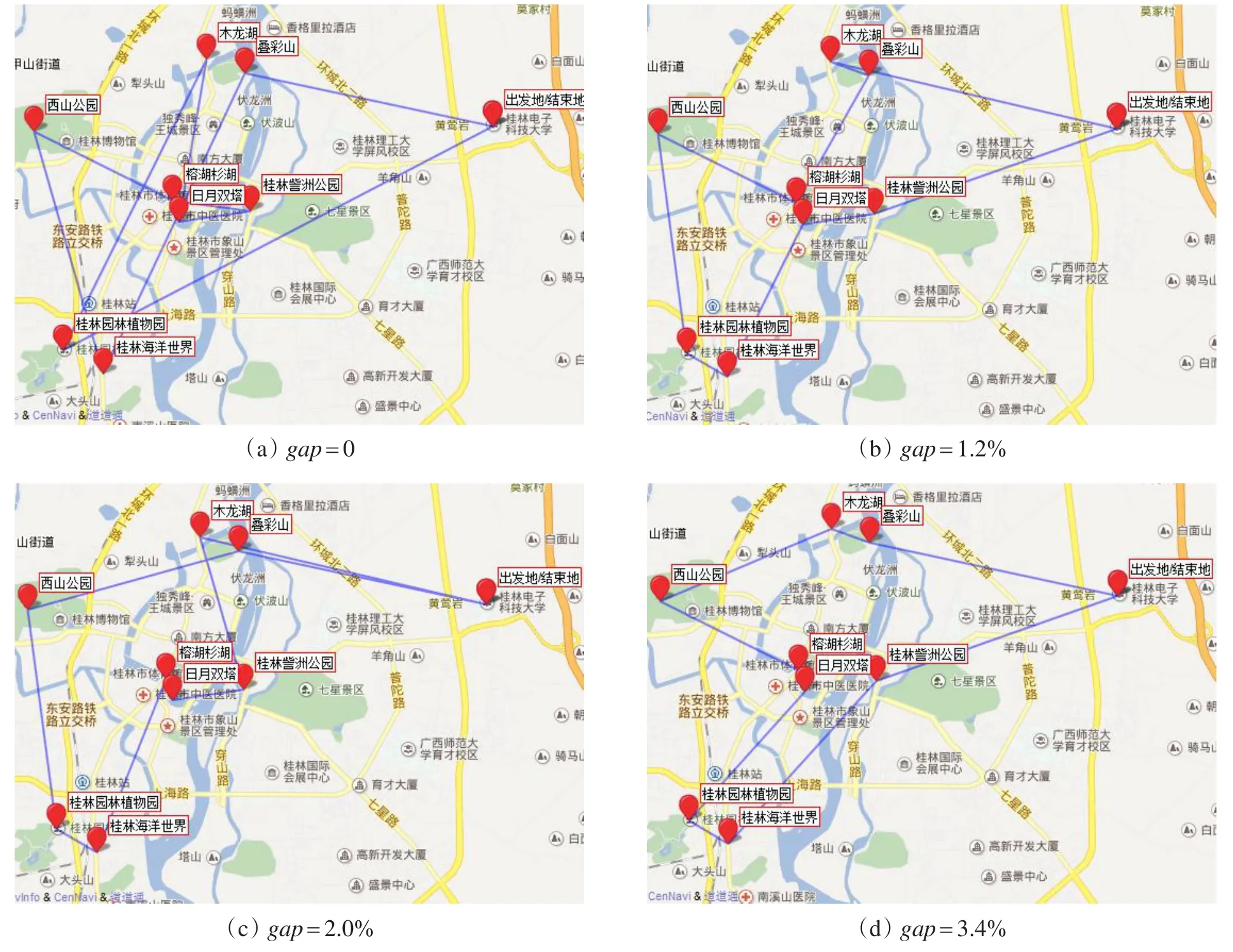
Fig.2 Trip itinerary for different gap图2　不同gap值的旅游线路

5.2WebGIS上线路展示效果分析

通过对ILS算法规划出的旅游线路的研究发现，线路交叉的现象较多，而经过对行程花费时间T的优化，则可以减少线路花费的时间，并有效减少旅游线路交叉现象。图2为ILS参数O1＝540，Cn＝1 320时随机选取的一条旅游线路。该条线路的ILS初始花费时间TILS＝1 286.7 min，经过优化后的时间为TCS＝1 252.2 min，时间减少率为3.4%，图2（a）到图2（d）是旅游线路gap值为0，1.2%，2.0%，3.4%时的线路在WebGIS上的展示效果。

从图2中可以看出，随着gap值的增大，行程花费时间逐渐降低，WebGIS地图上展示的旅游线路交叉现象也逐渐减少。分析发现，ILS算法在选择旅游景点的时候仅考虑尽可能地选择得分高的点，而没有考虑到当前的景点位置，因此在实际的旅游路线中会出现线路交叉现象，导致旅游行程时间的浪费，而经过ILS-CS优化后的线路在满足时间约束的同时并未出现线路交叉的现象，减少了行程花费时间，并且更符合人们的旅游习惯。

6　结束语

本文针对个性化旅游线路规划中存在的时间花费问题，提出了一种基于迭代局部搜索结合布谷鸟搜索的优化算法对旅游线路的时间花费进行优化。本文算法通过相关约束，采用迭代局部搜索算法取得了更符合用户旅游习惯的线路，再结合布谷鸟优化算法使得旅游的时间花费减少。本文方法使得旅游线路花费时间较优化前有较大的提升，并且规划出的旅游线路更符合用户的旅游习惯。该研究可以进一步延伸到将当地的天气以及实时交通约束考虑在个性化旅游线路规划中，使其更符合实际旅游的需要。

References：

[1] Cheverst K, Davies N, Mitchell K, et al. Developing a contextaware electronic tourist guide: some issues and experiences[C]// Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Hague, Netherlands, 2000: 17-24.

[2] Malaka R. Artificial intelligence goes mobile[C]//Artificial Intelligence in Mobile Systems—AIMS2000, Workshop in Conjunction with ECAI 2000, 2000: 5-7.

[3] Hagen K, Kramer R, Hermkes M, et al. Semantic matching and heuristic search for a dynamic tour guide[C]//Proceedings of the 2005 International Conference on Information and Communication Technologies in Tourism, Innsbruck, Austria, 2005. Vienna: Springer, 2005: 149-159.

[4] Kramer R, Modsching M, Ten Hagen K. A city guide agent creating and adapting individual sightseeing tours based on field trial results[J]. International Journal of Computational Intelligence Research, 2006, 2(2): 191-206.

[5] Vansteenwegen P, Souffriau W, Oudheusden D V. The orienteering problem: a survey[J]. European Journal of Operational Research, 2011, 209(1): 1-10.

[6] Chao I, Golden B L, Wasil E A. The team orienteering problem[J]. European Journal of Operational Research, 1996, 88 (3): 464-474.

[7] Souffriau W, Vansteenwegen P, Vertommen J, et al.Apersonalized tourist trip design algorithm for mobile tourist guides[J]. Applied Artificial Intelligence, 2008, 22(10): 964-985.

[8] Dumas Y, Desrosiers J, Gelinas E, et al. An optimal algorithm for the traveling salesman problem with time windows[J]. Operations Research, 1995, 43(2): 367-371.

[9] Vansteenwegen P, Souffriau W, Berghe G V, et al. Iterated local search for the team orienteering problem with time windows[J]. Computers & Operations Research, 2009, 36 (12): 3281-3290.

[10] Gavalas D, Konstantopoulos C, Mastakas K, et al. Clusterbased heuristics for the team orienteering problem with time windows[M]//Experimental Algorithms. Berlin, Heidelberg: Springer, 2013: 390-401.

[11] Yang Xinshe, Deb S. Cuckoo search via Lévy flights[C]// Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing. Piscataway, USA: IEEE, 2009: 210-214.

[12] Wei Xiangyuan,Yang Huihua, Xie Pumo. Research and implementation of parallel cuckoo search based on CUDA[J]. Journal of Frontiers of Computer Science and Technology, 2014, 8(6): 665-673.

[13] Durgun İ, Yildiz AR. Structural design optimization of vehicle components using cuckoo search algorithm[J]. Materials Testing, 2012, 54(3): 185-188.

[14] Yang Xinshe, Deb S. Engineering optimisation by cuckoo search[J]. International Journal of Mathematical Modelling and Numerical Optimisation, 2010, 1(4): 330-343.

附中文参考文献：

[12]韦向远,杨辉华,谢谱模.基于CUDA的并行布谷鸟搜索算法设计与实现[J].计算机科学与探索, 2014, 8(6): 665-673.

HOU Le was born in 1988. He is an M.S. candidate at School of Electronic Engineering and Automation, Guilin University of Electronic Technology. His research interests include pattern recognition and machine learning, etc.

侯乐（1988—），男，河南南阳人，桂林电子科技大学电子工程与自动化学院硕士研究生，主要研究领域为模式识别，机器学习等。

YANG Huihua was born in 1972. He received the Ph.D. degree from East China University of Science and Technology in 2005. Now he is a professor and Ph.D. supervisor at Beijing University of Posts and Telecommunications, and an adjunct professor at Guilin University of Electronic Technology. His research interests include intelligent information processing and machine learning, etc.

杨辉华（1972—），男，湖南常德人，2005年于华东理工大学获得博士学位，现为北京邮电大学自动化学院教授、博士生导师，桂林电子科技大学兼职教授，主要研究领域为智能信息处理，机器学习等。在国内外期刊及学术会议上发表科技论文30余篇，其中被SCI检索13篇，EI检索20篇，主持和参与多项国家自然科学基金、广西自然科学基金、广西高校优秀人才资助计划等项目。

FAN Yongxian was born in 1977. He received the Ph.D. degree from Shanghai Jiao Tong University in 2013. Now he is a lecturer at Guilin University of Electronic Technology. His research interests include pattern recognition and machine learning, etc.

樊永显（1977—），男，河南平顶山人，2013年于上海交通大学获得博士学位，现为桂林电子科技大学教师，主要研究领域为模式识别，机器学习等。发表学术论文10余篇，主持和参与多项国家自然科学基金项目。

LI Lingqiao was born in 1986. He is a Ph.D. candidate at School of Automation, Beijing University of Posts and Telecommunications. His research interests include intelligent information processing and machine learning, etc.

李灵巧（1986—），男，四川达县人，北京邮电大学自动化学院博士研究生，桂林电子科技大学助理研究员，主要研究领域为智能信息处理，机器学习等。

JIANG Shujie was born in 1989. She is an M.S. candidate at School of Electronic Engineering and Automation, Guilin University of Electronic Technology. Her research interests include pattern recognition and image processing, etc.蒋淑洁（1989—），女，湖北武汉人，桂林电子科技大学电子工程与自动化学院硕士研究生，主要研究领域为模式识别，图像处理等。在国内外期刊及学术会议上发表科技论文5篇，其中被SCI检索3篇，EI检索2篇。

Research on Personalized Trip Itinerary Based on ILS-CS Optimization*

HOU Le1, YANG Huihua1,2+, FAN Yongxian3, LI Lingqiao1,2, JIANG Shujie1
1. School of Electronic Engineering and Automation, Guilin University of Electronic Technology, Guilin, Guangxi 541004, China
2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
3. SchoolofComputerScienceandEngineering,GuilinUniversityofElectronicTechnology,Guilin,Guangxi541004,China
+ Corresponding author: E-mail: yhh@bupt.edu.cn

HOU Le, YANG Huihua, FAN Yongxian, et al. Research on personalized trip itinerary based on ILS-CS optimization. Journal of Frontiers of Computer Science and Technology, 2016, 10(1)：142-150.

Abstract:For the long travel time on trip itinerary planned by iterated local search (ILS), this paper proposes an optimization algorithm based on iterated local search with cuckoo search optimization to reduce the travel time. Firstly, this algorithm adopts ILS algorithm for solving an initial trip itinerary and several tourist attractions with some relevant objectives and constraints. Then, under the circumstance of no changing the time windows and the number of tourist attractions, this paper utilizes CS algorithm to minimize the travel time. The tourist route is obtained by above methods in this paper. It is more conform to travel habits and less travel time than existed ones. The experimental results on Daminaos and Guilin city data sets show that the average travel time of the proposed method reduces bybook=143,ebook=1478%, compared with only using ILS algorithm in itinerary optimization, and planning the itinerary for personalized tourists is more in line with user's choice.

Key words:trip itinerary planning; iterated local search; cuckoo search; orienteering problem with time windows; travel salesman problem with time windows

文献标志码：A

中图分类号：TP301

doi:10.3778/j.issn.1673-9418.1503030