应用非负矩阵分解模型的社区发现方法综述*

李亚芳，贾彩燕＋，于　剑1.北京交通大学计算机与信息技术学院，北京1000442.交通数据分析与挖掘北京市重点实验室，北京100044



应用非负矩阵分解模型的社区发现方法综述*

李亚芳1，2，贾彩燕1，2＋，于剑1，2
1.北京交通大学计算机与信息技术学院，北京100044
2.交通数据分析与挖掘北京市重点实验室，北京100044

* The National Natural Science Foundation of China under Grant Nos. 61473030，61370129（国家自然科学基金）; the Fundamental Research Funds for the Central Universities of China under Grant Nos. K15JB00070，2014JBM031（中央高校基本科研业务费专项资金）; the Opening Project of State Key Laboratory of Digital Publishing Technology（数字出版国家重点实验室专项课题）.

Received 2015-05，Accepted 2015-08.

CNKI网络优先出版：2015-08-12，http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1638.008.html

李亚芳，贾彩燕，于剑.应用非负矩阵分解模型的社区发现方法综述[J].计算机科学与探索，2016，10（1）：1-13.

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10（01）-0001-13

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel:＋86-10-89056056

摘要：非负矩阵分解（nonnegative matrix factorization，NMF）在提取高维数据中隐含模式和结构方面具有良好性能，已成为数据挖掘领域的热点研究之一。NMF作为无监督学习的有效工具，在模式识别、文本处理、多媒体数据分析以及生物信息学等研究领域得到了广泛应用。目前，已有工作将NMF模型应用于网络数据挖掘，发现网络中隐含的社区结构。对基于NMF的社区发现方法进行了总结，包括无监督的社区发现方法和半监督的社区发现方法，通过在实际网络和人工网络进行实验，比较分析了不同算法的性能，进一步研究了当前基于NMF发现社区结构所面临的挑战，并对下一步研究方向进行了展望。

关键词：数据挖掘；非负矩阵分解；社区发现

1　引言

复杂网络是描述自然界和社会系统的有力工具，现实世界中诸多复杂系统（如社会系统、科技系统、生物系统等）都可以用网络的形式表示。复杂网络是重要的多学科交叉研究领域，吸引了越来越多研究者的关注。研究发现，很多实际网络中的节点具有聚集化特性——“模块性”[1-2]，即网络存在明显的“社区结构”，主要表现为社区内部节点之间连接稠密，社区之间的节点连接稀疏。在实际网络中，社区结构通常具有特殊意义，发现社区结构对于理解网络的拓扑结构和功能特性具有重要的研究意义[3]。比如，在科研合作网中，一个社区通常表示某个科研领域，社区内的成员可能具有相似的研究方向，从而有利于提供精准的论文推荐以及选择合适的论文评审专家；蛋白质交互网中，一个社区代表一个组织的功能模块，因此有利于预测未知蛋白的功能。

目前，网络中社区发现的研究已经取得很多研究成果，可以大体将社区发现方法分为图切割方法[4-6]、目标函数优化方法[7-10]、聚类方法[11-13]和启发式方法[14-15]等。本质上，社区发现问题属于无监督学习范畴，因此研究者逐渐将目光投向无监督学习领域中取得成功应用的非负矩阵分解（nonnegative matrix factorization，NMF）模型处理网络中社区结构探测的问题。

NMF是一种新的矩阵分解思想，最早由Paatero 和Tapper[16]提出，称为正矩阵分解。1999年，Lee和Seung将NMF应用于图像处理并取得突出成果[17]。NMF相比于传统分解算法，具有实现简便，分解形式和分解结果有可解释性等优点，迅速得到各个领域研究者的高度重视。目前，NMF在理论研究和算法实现方向取得了突破性进展，研究发现，NMF与无监督学习的K-means方法和PLSI（probabilistic latent semantic indexing）等方法具有密切关系，且得到的结果有更好的解释性[18-20]。由于NMF在提取高维数据中隐含模式和结构方面具有良好能力，成为维数约简、无监督学习和预测等问题的有效工具，在模式识别[21]、文本处理[22-23]、多媒体数据分析[24]以及生物信息学[25]等研究领域得到了广泛应用。目前，也涌现出许多工作将NMF模型应用到网络社区发现中[26-37]，以发现网络中隐含的模块结构，并得到成功的应用。例如，He等人提出的NMFIB（nonnegative matrix factorization with iterative bipartition）模型[27]能够在蛋白质交互网络中得到更多统计显著的GO（gene ontology）项；Rsorakis等人提出的BNMF（Bayesian nonnegative matrix factorization）模型[30]，通过与传统层次聚类方法和谱聚类方法的对比，能够得到更加准确的社区结构。

本文对基于NMF的社区发现方法进行了总结，分析了当前研究面临的挑战，并对下一步研究方向进行了展望。本文组织结构为：第2章介绍非负矩阵分解基本模型以及应用于社区发现的解释；第3章介绍构建NMF模型中数据矩阵的方法；第4章对基于NMF的无监督社区发现方法进行总结；第5章介绍基于NMF的半监督社区发现方法；第6章进行实验比较和分析；最后指出基于NMF发现网络中社区结构遇到的挑战，并对未来的研究工作进行展望。

2　NMF基本概念和定义

非负矩阵分解的思想是寻找一个新的特征空间，将原数据在该空间进行投影，利用投影结果和空间信息重构原数据。给定一个非负的特征矩阵Xm×n，将其分解为两个低秩的非负矩阵W＝[Wic]∈和H＝[Hjc]∈（k≪n，m）的乘积，尽可能地逼近原来的数据矩阵X，即X≈WHT。形式化地，NMF模型可表示为如下优化问题：

min D（X，WHT）

s.t. W≥0，H≥0

其中，D（x，y）是衡量x与y差异性的损失函数，平方误差函数和广义KL散度函数是两种常用的损失函数。平方误差函数用两个矩阵差的Frobenius范数的平方表示，即DLSE（X，WHT）＝||X−WHT|，称该方法为NMFLSE。两个矩阵的广义KL散度（又称I-divergence）定义为：

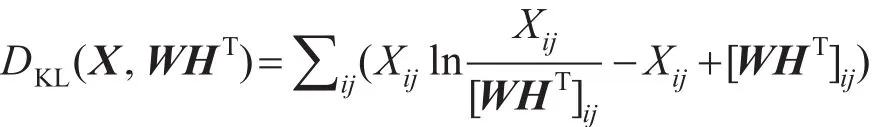
称该方法为NMFKL。损失函数的选择，通常依据不同的应用而定。为了优化该目标函数，常用的优化方法有多步迭乘法、梯度下降法、投影梯度法和交替最小二乘法等。

给定网络G＝（V，E），V＝{v1，v2，…，vn}表示节点集合，E＝{e1，e2，…，em}是边集合。通常用邻接矩阵A＝[Aij]n×n表示节点间的链接关系，矩阵对应元素的值表示边的强度，如果vi和vj之间不存在边，则Aij＝0。邻接矩阵是最常用的一种相似度表示，当然，也可以通过相似度计算得到新的相似度矩阵表示节点间的关系。本文用数据矩阵X表示通过相似度计算得到的网络中节点间的关系。

将标准的NMF模型应用于社区发现通常有两种理论解释。一种是基于NMF的基本思想，从节点的表示进行解释。数据矩阵X可以看作节点的特征表示矩阵，以邻接矩阵为例，每个节点通过与其他节点的链接情况来表示，即每一列是节点在n维空间的表示。W中的k个列向量看作新的特征空间下的一组基，H的每一行是在这组基下的新表示。因此，每个节点的表示向量x可以用W的列向量的线性组合进行逼近：x≈WhT，其中，h表示在各基向量的组合权重，代表节点到各个社区的隶属度。另一种是从网络中边的生成角度进行解释，用Wic和Hic分别表示从节点vi生成社区c中“出边”和“入边”的概率。因此，在k个社区中，生成连接节点vi和vj的边的概率为WikHjk，通过参数学习，用生成的边拟合实际网络中观测到的边，从而得到节点属于各社区的隶属度，学习到的W（H）的行表示每个节点属于各社区的程度。

通过以上两种方法得到的隶属度矩阵通常是节点的软化分矩阵，对应元素是取值为0到1的实数，表示每个节点属于各社区的程度。如果将节点指派到较大的隶属度对应的社区，则得到网络的重叠社区划分结果；如果将节点唯一指派到最大隶属度对应的社区，就得到非重叠划分的社区结构。

3　构建基于NMF社区发现方法的数据矩阵

NMF模型中的待分解数据矩阵X（又称特征矩阵），通常用邻接矩阵A表示，表示节点与网络中其他节点的链接关系和强度。然而，这种表示形式只能简单地呈现有直接连边的节点对之间的关系，无法用其他非直接连边的节点进行表示，得到的数据矩阵包含的信息有限。因此，根据网络的拓扑结构，通过相似度计算方法，得到新的数据矩阵成为基于NMF的社区发现方法中的重要内容。

根据数据矩阵的构造方法进行划分，大体可以分为以下几类：

（1）基于邻接矩阵的方法。如最简单的邻接矩阵A，以及通过矩阵A构建任意节点之间相似度的SH方法和SA方法[38]、Regular方法[39]等。

（2）基于物理过程的方法。该类方法将网络中任一节点看作源节点，通过一定时间下某个物理传播过程，得到该节点对网络中其他节点的影响程度积累，代表该节点与网络中节点的相似程度。代表方法有基于核扩散的SK方法[40]、信号传播方法（Signal）[41]、热量扩散方法[42]（Heat）、基于随机游走的LRW（local random walk）[43]和NRW（neighborhood random walk）方法[44]等。

（3）基于节点共有邻居的方法。如果两个节点之间共有邻居越多，其相似度越高，如Jaccard相似度方法[45]、SC方法[46]等。

（4）基于最短路径的方法。计算网络中节点的最短路径，如果两个节点距离越近，则相似度越高，代表方法有SP方法[47]等。

目前，根据网络中节点的链接关系，计算相似度矩阵构建数据矩阵的方法很多，更多相似度计算方法来构造数据矩阵X，可参见文献[48]。Wang等人曾初步比较了几种相似度方法[40]。本文对以上列举的12种数据矩阵构建方法进行了实验比较与分析，见6.1节。

根据数据矩阵分解的因子个数对算法进行划分，可以将基于NMF的社区发现方法大体分为两类：二因子分解和三因子分解。二因子分解，即将非负数据矩阵分解为两个低维的非负矩阵的乘积。进一步，可将其分为标准的非负矩阵分解和对称的非负矩阵分解。三因子分解是指数据矩阵通过3个因子的乘积来逼近，得到节点的隶属度矩阵和社区间的关联矩阵（表示社区与社区的关联强度）。根据是否添加了先验知识进行社区划分，可以将基于NMF的社区发现方法分为无监督的社区发现方法和半监督的社区发现方法。下面以此为划分准则，对基于NMF的社区发现方法进行总结。

4　基于NMF的无监督社区发现方法

Zhang等人[34]率先以邻接矩阵作为数据矩阵，采用标准的非负矩阵分解方法NMFLSE进行分解，得到新的特征空间的基矩阵W和节点在该特征空间的系数矩阵，即节点到社区的隶属度矩阵H。该分解模型是一个通用模型，能够同时处理有向网络和无向网络，可表示为：

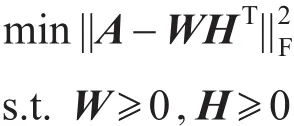
之后，根据具体的应用，相继提出不同的扩展模型来挖掘网络中的社区结构。网络根据边的方向性可分为有向网络和无向网络。Wang等人[32]针对无向网络，提出了对称的二因子模型SNMF（symmetric nonnegative matrix factorization），将数据矩阵分解为两个对称的低维非负矩阵的乘积，该模型表示为：

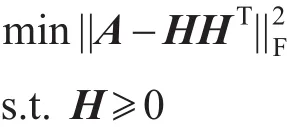
其中，H是隶属度矩阵，其每行元素的值表示每个节点隶属于各社区的程度。针对有向网络，对非对称数据矩阵进行三因子分解，得到节点对社区的隶属度矩阵和社区之间的关系矩阵，该ANMF（asymmetric nonnegative matrix factorization）模型表示为：

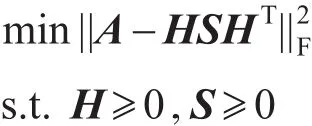
其中，S是社团间的关系矩阵，元素值表示社团间的关联强度。根据社区的定义，社区内节点连边紧密，社区间连边稀疏，因此通常得到的S矩阵的主对角元素值较大。

复杂网络分析中，邻接矩阵A通常用来表示网络中节点间的链接关系。一般认为，矩阵中的零元素意味着两个节点间不存在链接，然而，未被实际观测到的边也会给对应元素赋值为0。如果直接逼近邻接矩阵A，未观测的边会增加模型的噪音，影响最终的结果。并且考虑到实际网络中节点通常不会同时属于多个社区，因此Zhang等人[35]对隶属度矩阵用l1范数进行约束以增强其稀疏性，得到每个节点到各社区的概率，提出了BNMTF（bounded nonnegative matrix factorization）模型，用三因子的乘积对邻接矩阵中非零元素进行逼近，其定义如下：

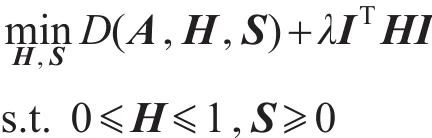
其中，I为单位向量；D为损失函数，可以采用均方误差DLSE（A，HSHT）或广义KL散度DKL（A，HSHT）。该模型通过逐个逼近邻接矩阵中非零元素，求解得到节点隶属于每个社区的概率矩阵。

Nguyen等人[29]为了更有效地处理有权网络，提出了iSNMF方法和iANMF方法，以广义KL散度作为损失函数，将邻接矩阵A分解为对称的二因子和三因子，即分别最小化如下目标函数：

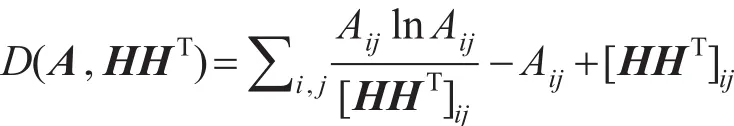
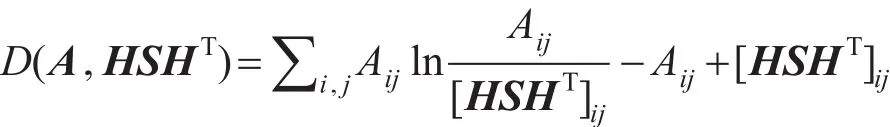
其中，H为节点的隶属度矩阵；S为社区间关系矩阵，其对应元素的值表示社团间连接的紧密程度。这两种方法不仅能处理有权网络，也能处理无权网络。

BNMF[30]是一种基于概率图模型的社区发现方法。根据实际的网络结构，构建一个图模型，通过学习模型的参数以拟合观测到的网络结构。假设实际网络的邻接矩阵为A，Â是期望的链接结构，Â由两个低秩的非负矩阵W＝[Wic]∈和H＝[Hjc]∈组成。对于节点vi和节点vj，其连边数（或链接权重）建模为＝，表示节点vi和vj在各社区中的共同参与程度。

图1给出了算法的概率图，其中βc为参数，其分布又受两个固定参数a和b影响，称为超参数。通过概率图模型，根据实际观测到的网络中节点的连边情况，最大化后验概率：

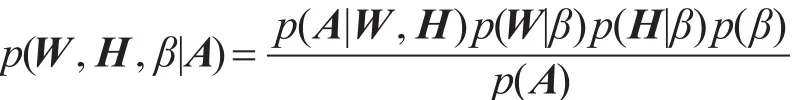
其中，p（A）为实际观测到的，属于自由参数。等价地，上式可以表示为最小化目标函数：

Ψ＝−lnp（A|W，H）−lnp（W|β）−lnp（H|β）−lnp（β）

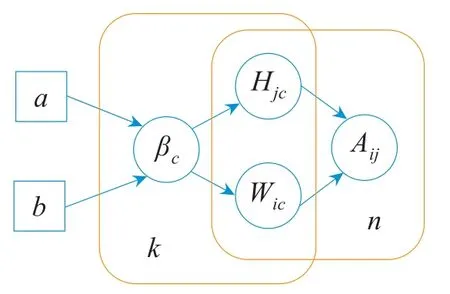
Fig.1 Graph model of W and H图1　生成矩阵W和H的图模型

通过交替地固定其中任意两个变量，更新另一个变量，不断更新W、H和β，直到算法收敛，得到了网络中每个节点到k个社区的隶属度矩阵H。

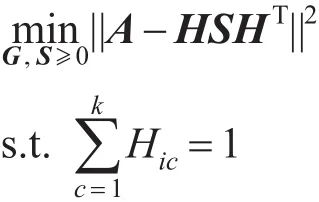
其中，H是节点到各社区的隶属度矩阵；S是社区度的对角矩阵，对角元素的值表示各社区中期望的节点度。由于S是一个对角矩阵，则得到如下变换：

HSHT＝HS1/2S1/2HT＝（HS1/2）（HS1/2）T＝UUT

因此，目标函数退化为对称的矩阵分解形式：

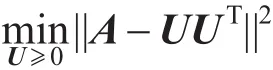
通过求解得到U，根据上式等价变换和对H的约束，求得S＝（IU）2，其中I为n维列向量，那么得到U＝HS1/2，进而得到隶属度矩阵H＝U（S1/2）−1。

阿里不明白这些，只觉得好热闹，他不禁高兴起来。拍着巴掌又蹦又跳地大声唱：“阿里的弟弟过来了!阿里的爸爸过来了!”

以上介绍的方法都是通过得到节点对各社区的隶属度，从而得到节点的划分。He等人[27]从链接社区的角度，利用生成模型提出基于NMF的链接社区发现方法NMFIB。首先，定义社区c的规模为Bc，即该社区内边权重和的两倍，ϕic表示从社区c生成一条连接节点vi的边的概率，从社区c连边所有节点的概率和为1。那么，生成一条连接节点vi和vj的边的概率为Âij＝∑cBcϕicϕjc。对于一个有m条边的网络，得到如下目标函数：

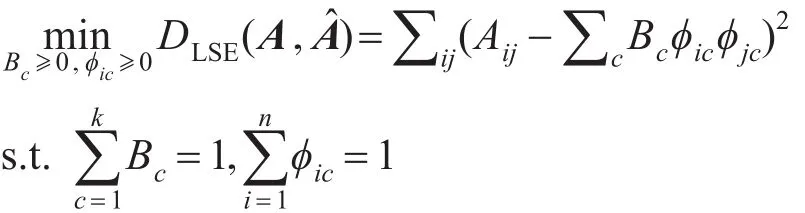
通过引入辅助变量H，将该问题转化为带约束的对称矩阵分解模型：

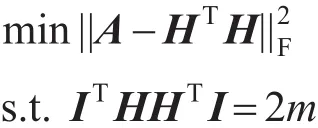
其中，Hic＝ϕic，I为n维列向量。通过梯度下降法，对Hic进行更新直至算法收敛。根据约束条件＝1，易得到每条边属于各社区的隶属度ϕic＝Hic/∑iHic。根据隶属度矩阵，实现网络中边的划分，从而得到边连接的节点的社区指派：属于同一类的边所对应的节点属于同一社区，如果存在节点同时属于多个社区，则根据边的隶属度将节点指派到最大隶属度对应的社区。

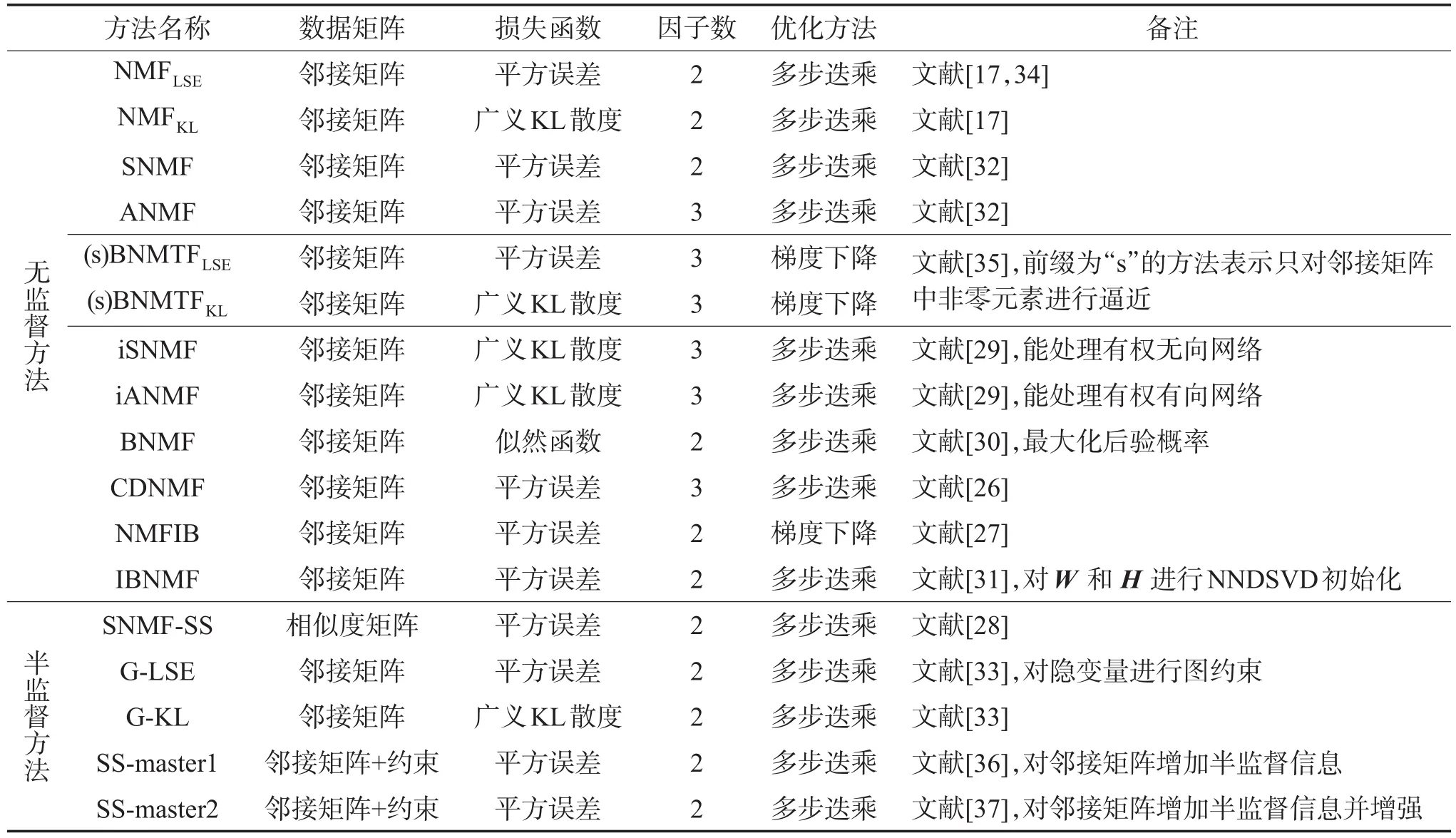
Table 1 Statistics of community detection algorithms based on NMF表1　基于NMF的社区发现方法统计表

基于NMF的社区发现方法取得了一定的研究成果，然而传统方法通常对初始矩阵W和H进行随机初始化，这样会造成结果的不稳定，而且降低算法的收敛速度。为解决初始化问题，Tang等人提出了IBNMF（initialized Bayesian nonnegative matrix factorization）方法[31]。该方法基于对称的非负矩阵分解模型BNMF[30]，通过NNDSVD（nonnegative double singular value decomposition）[49]近似方法对W和H进行初始化，明显提高了算法的收敛速度，而且能够得到更加稳定的结果。更多基于NMF的无监督社区发现方法的统计信息见表1上部分。

5　基于NMF的半监督社区发现方法

以上基于NMF的社区发现方法只根据网络中节点间的链接关系发现社区结构，属于无监督的社区发现方法。如果考虑网络的先验信息，则得到半监督的社区发现方法。该类方法能够更准确地发现复杂网络中的社团结构，尤其在社区结构不清晰的情况下，仍能得到较好的结果。

Ma等人[28]融合网络的领域知识对原来的数据矩阵X进行更新来指导节点的聚类过程，提出了半监督的对称非负矩阵分解方法SNMF-SS。他们将节点对之间的约束分为两类：“一定链接”（must-link）约束指属于CML的节点对一定属于同一个社区；“不能链接”（cannot-link）约束指属于CCL的节点对分属不同社区。文中，首先通过SK方法[40]构造数据矩阵X。通过向X中增加约束，使得处于同一个社区的两个节点具有较高相似性，降低属于不同社区的节点对间的相似度值，得到新的数据矩阵：

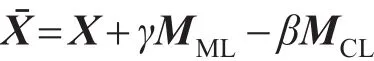
其中，γ和β是参数；MML和MCL是通过以上介绍的相似度方法构造的两个相似度矩阵。文中选用对称矩阵分解，用两个对称矩阵的乘积逼近新的数据矩阵。因此，SNMF-SS最小化如下目标函数：

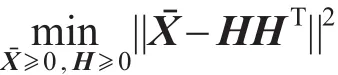
SNMF-SS采用不同的相似度方法构造节点对的约束矩阵，通过对原始相似度矩阵进行补充，得到新的数据矩阵，从而增强原来待分解矩阵。特殊地，当γ＝β＝0时，SNMF-SS退化为无监督的对称非负矩阵分解方法。

类似地，Zhang直接对网络的邻接矩阵增加成对的约束（“一定链接”和“不能链接”），提出了半监督的社区发现方法SS-master1[36]。成对约束中，如果两个节点属于同一个社区，对应邻接矩阵的相应元素取值为α（文中α＝2）；如果两个节点一定不属于同一个社区，则邻接矩阵对应元素取值为0。

Zhang等人在对邻接矩阵直接增加约束后，通过考虑节点对约束的传递性，对增加的约束进一步增强，提出了增强的半监督社区发现方法SS-master2[37]。约束的传递性（逻辑推理）主要从以下两点考虑：

（1）朋友的朋友是朋友。如果节点i和k属于同一个社区，节点i和t属于同一个社区，那么节点k和t也属于同一社区。

（2）敌人的朋友也是敌人。如果节点i和k属于同一个社区，节点i和t属于不同的社区，那么节点k 和t分属不同的社区。

对约束后的邻接矩阵，通过标准的非负矩阵分解得到节点的隶属度矩阵，从而实现对节点的划分。Zhang通过实验发现，“一定链接”约束相比于“不能链接”约束能够得到更好的划分结果，说明“一定链接”能够为提高算法的准确率提供更多的先验知识。

以上介绍的半监督的社区发现方法都是根据先验知识对待分解的数据矩阵X进行更新，Yang等人[33]提出一种基于节点隐空间约束的模型，对属于同一社区的节点增加图正则化项，使得越相近的节点在隐空间的向量表示尽可能相近。若分别用均方距离和广义KL散度作为节点间的度量，即最小化如下目标函数，分别记为G-LSE和G-KL： FKL（A，W，H）＝

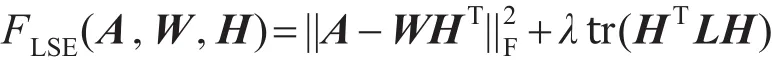
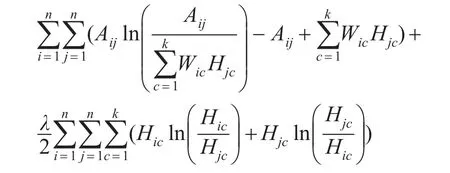
其中，λ是调节网络拓扑结构信息和节点先验信息所占比重的参数。L＝D−C是拉普拉斯矩阵，C是节点的约束矩阵，如果vi和vj属于同一个社区，那么Cij≠0，D是对角矩阵（Dii＝∑jCij）。该方法通过考虑“一定链接”的约束，使得属于同一社区的两个节点，在低维空间的表示更相近（距离更近），从而能够得到更加准确的划分结果。更多基于NMF的半监督社区发现方法的统计信息见表1下部分。

6　实验对比和分析

为了比较基于NMF的社区发现方法的性能并进行分析，以准确率和标准互信息作为评价指标，选取6个真实数据和两组人工生成网络进行测试。实际网络包括经典的Zachary空手道俱乐部网络[45]、海豚关系网络[50]、美国大学足球赛网络[2]、美国政治书籍网络（http://www.orgnet.com）、博客网络[51]和蛋白质交互（protein-protein interaction，PPI）网络[51]。人工生成网络包括的GN网络[1]和LFR网络[52]。所有实验都是用Matlab实现，在Intel Core CPU 3.00 GHz，4.00 GB内存的Windows 8（64位）计算机上运行，各社区发现方法的迭代终止条件为最大迭代次数达到200或两次迭代目标函数值的变化小于e−10。

6.1数据矩阵对社区发现结果分析

首先，比较数据矩阵对社区划分结果的影响。在6个真实网络中用12种矩阵构建方法构造数据矩阵，用NMFLSE

[17，34]对数据矩阵进行分解。为保证实验的公平性，在同一数据集上，每次采用同一组初始化因子矩阵W和H进行随机初始化（IBNMF[31]用NNDSVD进行初始化），表2和表3列出了20次运行的平均结果。从表中可以得到以下结论：

（1）通过相似度计算得到新的数据矩阵对网络进行表示，能够更多地捕获到网络中节点间的关系信息，因此社区划分准确性往往高于直接采取简单的邻接矩阵。

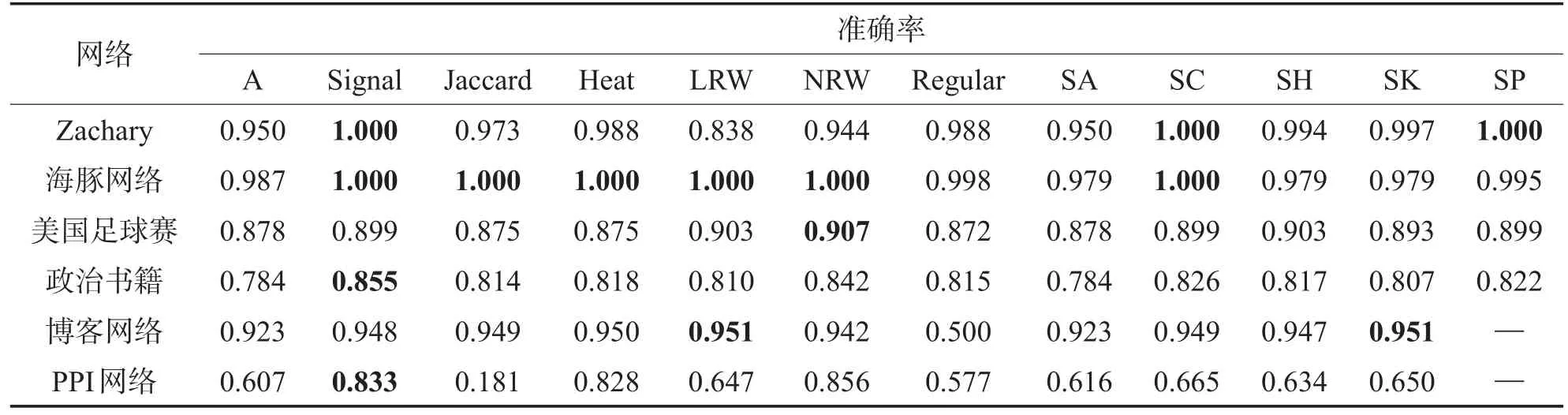
Table 2 Accuracy comparison of different data matrices表2　采取不同数据矩阵的准确率比较

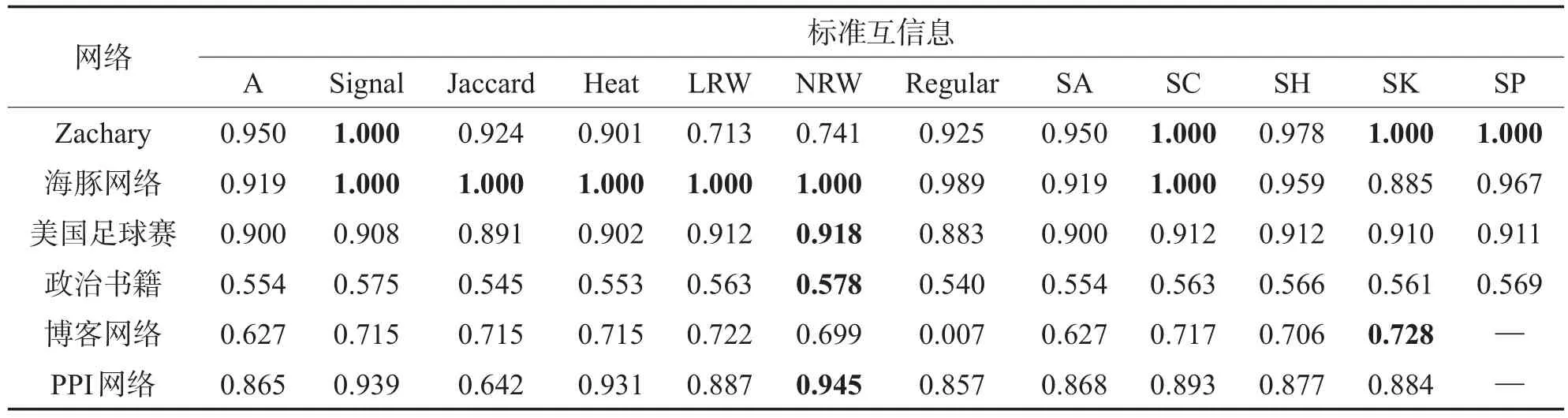
Table 3 Normalized mutual information comparison of different data matrices表3　采取不同数据矩阵的标准互信息比较

（2）不同的相似度矩阵适应的网络类型不同，因此在不同数据集上得到的结果不同。总体上，基于物理过程的方法，如信号传播方法Signal和局部随机游走方法NRW表现出较好的性能。

（3）进行相似度计算作为NMF的预处理步骤往往会增加算法的复杂度，因此在实际应用中，往往需要在算法的准确率和效率之间进行合理折中。

6.2基于NMF无监督社区发现方法比较

本节对基于NMF的无监督社区发现方法进行比较，结果如表4所示，所有方法都以网络的邻接矩阵作为数据矩阵。通过表4可以发现，以平方误差作为损失函数得到的结果通常比广义KL散度好。还观察到模型的求解方法会影响算法的效率，例如BNMTF方法采取的优化方法需要逐个对矩阵中的元素进行更新，算法复杂度较高，因此不适用于处理规模较大的网络。所有算法中，NMFIB方法通过对边进行划分，得到网络中节点的社区结构在几个数据集中都表现出比较好的性能。IBNMF方法通过NNDSVD对初始分解因子W和H进行初始化，在Zachary网络、海豚网络和政治书籍网络中取得了较好结果，划分结果更加鲁棒。

6.3基于NMF半监督社区发现方法比较

本节通过在人工生成的GN网络[1]和LFR网络[52]上进行实验，以无监督的NMFLSE[17]作为基准方法，比较半监督社区发现方法G-LSE[33]、G-KL[33]、SS-master1[36]、SS-master2[37]和SNMF-SS[28]的性能。实验中，SNMF-SS的参数设置为γ＝0.3，β＝0.001，G-LSE和G-KL中λ＝5，SS-master1和SS-master2中α＝2。为了保证实验的公平性，均匀随机选择增加的约束对，在不同先验信息约束下，各算法选取同一组初始化因子进行随机初始化，每个约束下运行算法20次。图2为Zout＝Zin＝8时的GN网络，图3为LFR网络（节点数n＝1 000，μ＝0.9），横坐标表示增加的约束对比例，纵坐标表示算法的性能。通过比较，可以得到如下结论：

（1）与未增加任何约束的NMFLSE比较，通过增加先验知识能够提高网络中社区划分的准确率。

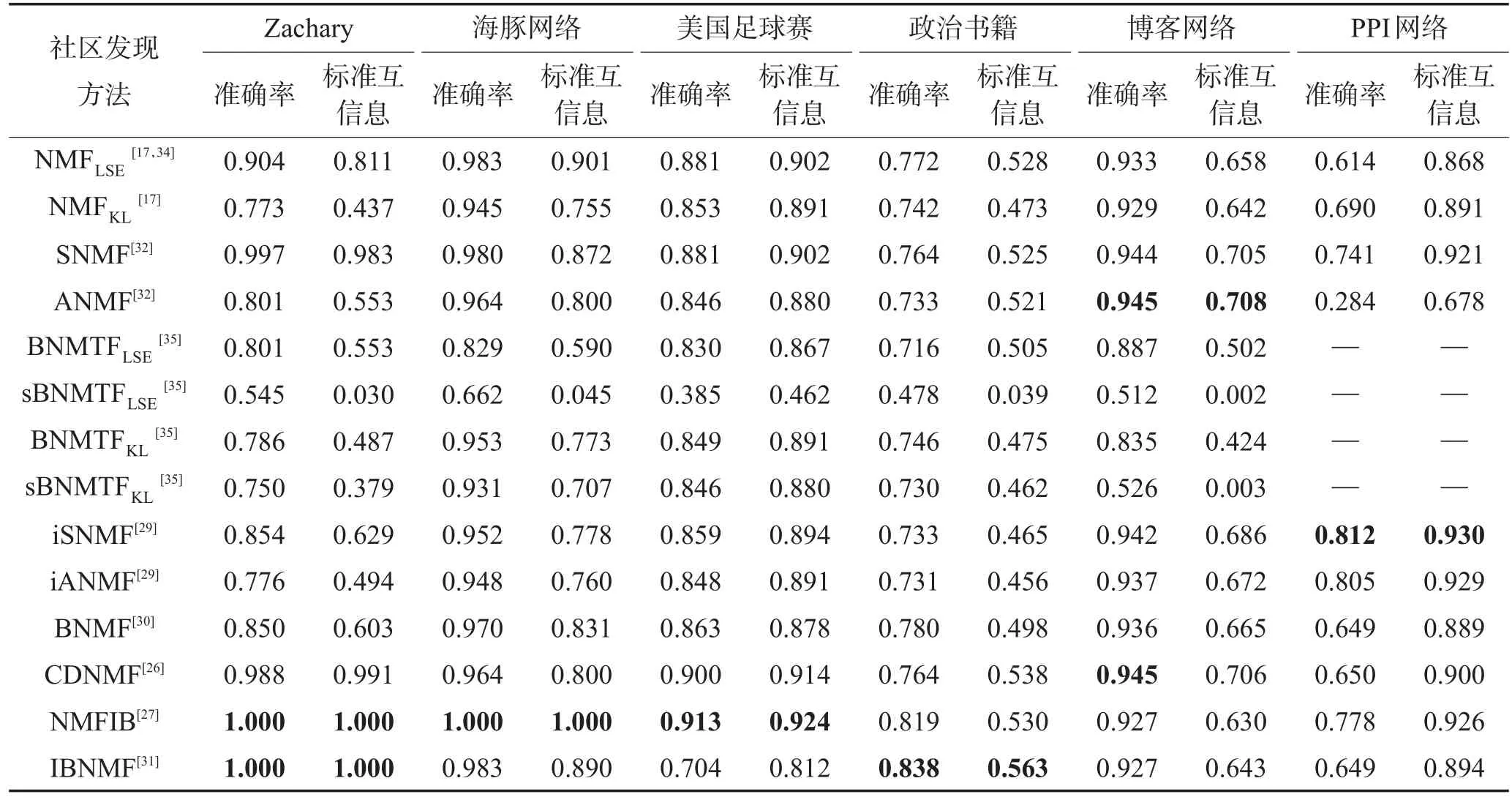
Table 4 Comparison results on accuracy and normalized mutual information of different algorithms on real-world networks表4　算法在实际网络中的社区划分准确率和标准互信息比较

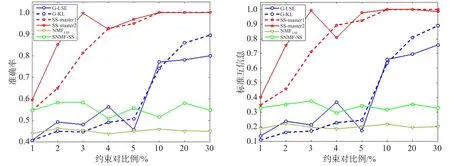
Fig.2 Comparison results on GN networks图2　GN网络上的结果比较

（2）通过对G-LSE和G-KL进行比较，选取平方误差作为损失函数往往得到更好的结果，这与无监督的社区发现方法得到的结果一致。

（3）在5个半监督社区发现方法中，简单地在邻接矩阵上增加约束的方法，如SS-master1和SS-master2方法能够得到较好的划分效果，其中通过逻辑推理进行增强的SS-master2表现出最好的效果，尤其当增加的约束比例较低时，SS-master2能够显著提高社区划分的准确率。

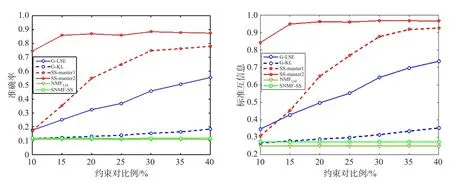
Fig.3 Comparison results on LFR networks（n＝1 000，μ＝0.9）图3　LFR网络上的结果比较（n＝1 000，μ＝0.9）

7　结束语

本文对目前已有的基于NMF的社区发现方法进行了总结，通过在人工网络和实际网络上实验，对不同的算法性能进行了比较和分析。NMF已经在图像处理、生物信息处理和文本处理等领域得到了成功应用，但是在复杂网络分析中的应用仍处于起步阶段。尽管现有的工作对网络中社区发现问题进行了一定的研究，但是还有很多问题值得深入探索。

（1）NMF初始化。NMF需要对初始因子W和H进行初始化，好的初始化因子能够极大提高算法的准确率和收敛速度。目前常通过随机初始化方法对因子矩阵赋初始值，此时不能对算法给出好的估计，会影响算法的性能。目前已经提出一些NMF初始化方法，如K均值初始化、中心初始化、NNDSVD等，但是初始化作为NMF的预处理步骤会增大算法的计算复杂度，而且不同的NMF求解算法对因子的初始化要求也不同，如有些算法需要同时对两个因子进行初始化，有些则只需要初始化W。因此，针对社区发现方法的特殊应用，如何设计有效的因子矩阵初始化方法，以及确定初始化的因子矩阵个数是有待解决的问题。

（2）隐含因子数的确定。目前基于NMF的社区发现方法中，大都需要提前设定隐含因子数k，即社区划分的个数。一种简单的处理方法是通过设置不同的k值，从中选择使得划分结果最好的作为最终的划分，这无疑也会降低算法的效率。尽管现在有些方法提出了k选择的策略，如BNMF首先设置最大可能的社区个数k0，通过迭代隐含因子W和H，根据非零列（非零行）的个数减小k0，当算法收敛时，得到最终的k0为社区的个数。NMFIB则通过迭代二分方法，将初始整个网络首先通过NMF划分为两部分，然后对得到的两个子网络划分成两部分，每次划分时，通过一定规则判定是否接受此次划分，当算法结束时，得到社区的个数。然而这些方法都是嵌入在社区划分过程中，容易受到多种因素的影响，如矩阵的初始和更新情况等，可能会得到不同的k，难以准确确定社区的个数。因此，社区划分个数k的选择值得进一步研究。

（3）处理具有复杂特性的网络。随着社交媒体的发展，实际网络呈现出更加复杂的特性，如网络大多具有动态变化性，如何应用NMF模型发现动态网络中的社区结构及其演变规律，设计在线的NMF算法为探索网络中社区结构提出新的要求。另外，目前网络多呈异构特性，网络不仅包含节点间的链接关系，而且还包含丰富的节点和链接的属性信息，如何根据网络中节点的链接关系和属性信息，应用NMF模型处理这类复杂的网络为进一步的研究提出新的挑战。

（4）处理大规模网络数据。目前网络规模成指数级增长，为了处理大规模网络数据，采取快速的求解算法以提高NMF收敛速率提供了一条解决思路。然而，为了更有效挖掘大规模网络中的社区结构，设计分布式NMF以及并行NMF策略将成为重要的研究内容，也是亟待解决的问题。

References:

[1] Girvan M，Newman M E. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences，2002，99（12）: 7821-7826.

[2] Newman M E，Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E，2004，69（2）: 026113.

[3] Newman M E. The structure and function of complex networks[J]. SIAM Review，2003，45（2）: 167-256.

[4] Fiedler M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal，1973，23（2）: 298-305.

[5] Pothen A，Simon H D，Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J]. SIAM Journal on Matrix Analysis and Applications，1990，11（3）: 430-452.

[6] Shiga M，Takigawa I，Mamitsuka H. A spectral clustering approach to optimally combining numerical vectors with a modular network[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，San Joze，USA，Aug 12-15，2007. New York，USA: ACM，2007: 647-656.

[7] Aldecoa，R，Marín I. Surprise maximization reveals the community structure of complex networks[J]. Scientific Reports，2013，3: 1060.

[8] Blondel V D，Guillaume J L，Lambiotte R，et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment，2008（10）: P10008.

[9] Jiang Yawen，Jia Caiyan，Yu Jian. An efficient community detection algorithm using greedy surprise maximization[J]. Journal of Physics A: Mathematical and Theoretical，2014，47（16）: 165101.

[10] Newman M E. Detecting community structure in networks[J]. The European Physical Journal B: Condensed Matter and Complex Systems，2004，38（2）: 321-330.

[11] Fortunato S，Latora V，Marchiori M. Method to find community structures based on information centrality[J]. Physical Review E，2004，70（5）: 056104.

[12] Frey B J，Dueck D. Clustering by passing messages between data points [J]. Science，2007，315（5814）: 972-976.

[13] Jiang Yawen，Jia Caiyan，Yu Jian. An efficient community detection method based on rank centrality[J]. Physica A: Statistical Mechanics and Its Applications，2013，392（9）: 2182-2194.

[14] Mete M，Tang Fusheng，Xu Xiaowei，et al. A structural approach for finding functional modules from large biological networks[J]. BMC Bioinformatics，2008，9（S9）: S19.

[15] Xu Xiaowei，Yuruk N，Feng Zhidan，et al. Scan: a structural clustering algorithm for networks[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，San Joze，USA，Aug 12-15，2007. New York，USA:ACM，2007: 824-833.

[16] Paatero P，Tapper U. Positive matrix factorization: a nonnegative factor model with optimal utilization of error estimates of data values[J]. Environmetrics，1994，5（2）: 111-126.

[17] Lee D D，Seung H S. Learning the parts of objects by nonnegative matrix factorization[J]. Nature，1999，401（6755）: 788-791.

[18] Ding C，Li Tao，Jordan M I. Convex and semi-nonnegative matrix factorizations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（1）: 45-55.

[19] Ding C，Li Tao，Peng Wei. On the equivalence between nonnegative matrix factorization and probabilistic latent semantic indexing[J]. Computational Statistics＆Data Analysis，2008，52（8）: 3913-3927.

[20] Ding C，He Xiaofeng，Simon H D. On the equivalence of nonnegative matrix factorization and spectral clustering[C]// Proceedings of the 5th International Conference on Data Mining，Newport Beach，USA，Apr 21-23，2005. Philadelphia，USA: SIAM，2005: 606-610.

[21] Li S Z，Hou Xinwen，Zhang Hongjiang，et al. Learning spatially localized，parts-based representation[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，Kauai，Hawaii，USA，Dec 8-14，2001. Piscataway，USA: IEEE，2001: I-207-I-212.

[22] Pauca V P，Shahnaz F，Berry M W，et al. Text mining using non-negative matrix factorizations[C]//Proceedings of the 4th International Conference on Data Mining，Lake BuenaVista，USA，Apr 22-24，2004. Philadelphia，USA: SIAM，2004: 452-456.

[23] Shahnaz F，Berry M W，Pauca V P，et al. Document clustering using nonnegative matrix factorization[J]. Information Processing＆Management，2006，42（2）: 373-386.

[24] Cooper M，Foote J. Summarizing video using non-negative similarity matrix factorization[C]//Proceedings of the IEEE 5th Workshop on Multimedia Signal Processing，Virgin Islands，USA，Dec 9-11，2002. Piscataway，USA: IEEE，2002: 25-28.

[25] Pascual-Montano A，Carazo J M，Kochi K，et al. Nonsmooth nonnegative matrix factorization（nsNMF）[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，28（3）: 403-415.

[26] Cao Xiaochun，Wang Xiao，Jin Di，et al. Identifying overlapping communities as well as hubs and outliers via nonnegative matrix factorization[J]. Scientific Reports，2013，3: 2993.

[27] He Dongxiao，Jin Di，Baquero C，et al. Link community detection using generative model and nonnegative matrix factorization[J]. PloS One，2014，9（1）: e86899.

[28] Ma Xiaoke，Gao Lin，Yong Xuerong，et al. Semi-supervised clustering algorithm for community structure detection in complex networks[J]. Physica A: Statistical Mechanics and Its Applications，2010，389（1）: 187-197.

[29] Nguyen N P，Thai M T. Finding overlapped communities in online social networks with nonnegative matrix factorization[C]//Proceedings of the 2012 Military Communications Conference，Orlando，USA，Oct 29-Nov 1，2012. Piscataway，USA: IEEE，2012: 1-6.

[30] Psorakis I，Roberts S，Ebden M，et al. Overlapping community detection using Bayesian non-negative matrix factorization[J]. Physical Review E，2011，83（6）: 066114.

[31] Tang Xianchao，Xu Tao，Feng Xia，et al. Uncovering community structures with initialized Bayesian nonnegative matrix factorization[J]. PloS One，2014，9（9）: e107884.

[32] Wang Fei，Li Tao，Wang Xin，et al. Community discovery using nonnegative matrix factorization[J]. Data Mining and Knowledge Discovery，2011，22（3）: 493-521.

[33] Yang Liang，Cao Xiaochun，Jin Di，et al. A unified semisupervised community detection framework using latent space graph regularization[J]. IEEE Transactions on Cybernetics，2015，45（11）: 2585-2598.

[34] Zhang Shihua，Wang Ruisheng，Zhang Xiangsun. Uncovering fuzzy community structure in complex networks[J]. Physical Review E，2007，76（4）: 046103.

[35] Zhang Yu，Yeung D Y. Overlapping community detection via bounded nonnegative matrix tri-factorization[C]//Proceedings of the 18th International Conference on Knowledge Discovery and Data Mining，Beijing，China，Aug 12-16，2012. Piscataway，USA: IEEE，2012: 606-614.

[36] Zhang Zhongyuan. Community structure detection in complex networks with partial background information[J]. Europhysics Letters，2013，101（4）: 48005.

[37] Zhang Zhongyuan，Sun Kaidi，Wang Siqi. Enhanced community structure detection in complex networks with partial background information[J]. Scientific Report，2013，3: 3241. [38] Wang Ruisheng，Zhang Shihua，Wang Yong，et al. Clustering complex networks and biological networks by nonnegative matrix factorization with various similarity measures[J]. Neurocomputing，2008，72（1/3）: 134-141.

[39] Leicht E，Holme P，Newman M E. Vertex similarity in networks[J]. Physical Review E，2006，73（2）: 026120.

[40] Kondor R I，Lafferty J. Diffusion kernels on graphs and other discrete input spaces[C]//Proceedings of the 19th International Conference on Machine Learning，Sydney，Australia，Jul 8-12，2002. New York，USA:ACM，2002: 315-322.

[41] Hu Yanqing，Li Menghui，Zhang Peng，et al. Community detection by signaling on complex networks[J]. Physical Review E，2008，78（1）: 016115.

[42] Ma Hao，King I，Lyu M R. Mining Web graphs for recommendations[J]. IEEE Transactions on Knowledge and Data Engineering，2012，24（6）: 1051-1064.

[43] Liu Weiping，Lv Linyuan. Link prediction based on local random walk[J]. Europhysics Letters，2010，89（5）: 58007.

[44] Zhou Yang，Cheng Hong，Yu J X. Graph clustering based on structural/attribute similarities[J]. Proceedings of the VLDB Endowment，2009，2（1）: 718-729.

[45] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research，1977，33（4）: 452-473.

[46] Jiao Junyong，Hu Di，Zhang Zhongyuan. A novel similarity measurement for community structure detection[C]//Procee-dings of the 4th International Conference on Intelligent Human-Machine Systems and Cybernetics，Nanchang，China，Aug 26-27，2012. Piscataway，USA: IEEE，2012: 301-306.

[47] Gustafsson M，Hörnquist M，Lombardi A. Comparison and validation of community structures in complex networks[J]. Physica A: Statistical Mechanics and Its Applications，2006，367: 559-576.

[48] Lv Linyuan，Zhou Tao. Link prediction in complex networks: a survey[J]. Physica A: Statistical Mechanics and Its Applications，2011，390（6）: 1150-1170.

[49] Boutsidis C，Gallopoulos E. SVD based initialization: a head start for nonnegative matrix factorization[J]. Pattern Recognition，2008，41（4）: 1350-1362.

[50] Lusseau D，Schneider K，Boisseau O J，et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology，2003，54（4）: 396-405.

[51] Adamic L A，Glance N. The political blogosphere and the 2004 US election: divided they blog[C]//Proceedings of the 3rd International Workshop on Link Discovery，Chicago，USA，Aug 21-24，2005. New York，USA:ACM，2005: 36-43.

[52] Lancichinetti A，Fortunato S，Radicchi F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E，2008，78（4）: 046110.

LI Yafang was born in 1988. She is a Ph.D. candidate at Beijing Jiaotong University，and the student member of CCF. Her research interests include data mining and complex network analysis，etc.

李亚芳（1988—），女，河北沧州人，北京交通大学博士研究生，CCF学生会员，主要研究领域为数据挖掘，复杂网络分析等。

JIA Caiyan was born in 1976. She received the Ph.D. degree in computer software and theory from Institute of Computing Technology，Chinese Academy of Sciences in 2004. Now she is an associate professor at Beijing Jiaotong University，and the member of CCF. Her research interests include data mining，bioinformatics and complex network analysis，etc.

贾彩燕（1976—），女，宁夏石嘴山人，2004年于中国科学院计算技术研究所计算机软件与理论专业获得博士学位，现为北京交通大学计算机学院副教授，CCF会员，主要研究领域为数据挖掘，生物信息学，复杂网络分析等。

YU Jian was born in 1969. He received the Ph.D. degree from Department of Mathematics，Peking University in 2000. Now he is a professor and Ph.D. supervisor at Beijing Jiaotong University，and the senior member of CCF. His research interests include machine learning，data mining and image segmentation，etc.

于剑（1969—），男，山东淄博人，2000年于北京大学数学系获得博士学位，现为北京交通大学计算机学院教授、博士生导师，CCF高级会员，主要研究领域为机器学习，数据挖掘，图像分割等。

Survey on Community Detection Algorithms Using Nonnegative Matrix Factorization Model*

LI Yafang1，2，JIACaiyan1，2＋，YU Jian1，2
1. School of Computer and Information Technology，Beijing Jiaotong University，Beijing 100044，China
2. Beijing Key Lab of Traffic Data Analysis and Mining，Beijing 100044，China
＋Corresponding author: E-mail: cyjia@bjtu.edu.cn

LI Yafang，JIA Caiyan，YU Jian. Survey on community detection algorithms using nonnegative matrix factorization model. Journal of Frontiers of Computer Science and Technology，2016，10（1）：1-13.

Abstract:Nonnegative matrix factorization（NMF）has good ability in extracting inherent patterns and structures in high dimensional data and has been one of hot research topics in data mining. Nonnegative matrix factorization is a tool for unsupervised learning and has been widely applied in pattern recognition，text mining，image processing and bioinformatics. Recently，many researchers have paid attention to network-based data mining via nonnegative matrix factorization in order to detect cohesively connected community in networks. This paper summarizes community detection algorithms using nonnegative matrix factorization，including unsupervised methods and semi-supervised algorithms. Then，this paper compares and analyzes the performance of different algorithms by conducting experiments on artificial networks and real-world networks. Finally，this paper discusses challenges and further work on detecting communities in networks by using nonnegative matrix factorization.

Key words:data mining; nonnegative matrix factorization; community detection

文献标志码：A

中图分类号：TP181

doi:10.3778/j.issn.1673-9418.1505047