系统域网络基于消减策略网络断层扫描方法*

黄　杰，陈　琳，王斌锋国防科学技术大学计算机学院，长沙410073



系统域网络基于消减策略网络断层扫描方法*

黄杰＋，陈琳，王斌锋
国防科学技术大学计算机学院，长沙410073

* The National Natural Science Foundation of China under Grant No. 61379148（国家自然科学基金）.

Received 2015-04，Accepted 2015-06.

CNKI网络优先出版：2015-06-12，http://www.cnki.net/kcms/detail/11.5602.TP.20150612.1122.001.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10（01）-0065-09

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel:＋86-10-89056056

摘要：系统域网络是高性能计算机、数据中心的重要组成部分，当前系统域网络存在网络规模庞大，内部链路繁多，网络流量行为复杂和各种应用对网络性能状况敏感度高等特点，致使采用传统网络断层扫描方法进行性能测量的计算复杂度呈指数级增长。针对上述问题提出了一种基于消减策略的网络断层扫描方法（network tomography based on reduction strategy，NTRS）。该方法提出了预处理原则对实际物理拓扑进行策略约束，充分利用内部链路已知的性能信息缩小性能测量网络区域和关键链路覆盖，依据测量结果计算链路性能协方差，筛除性能状况较好的链路集合，实现链路数量的有效约简，进而很大程度上提高了网络诊断的准确性。通过模拟实验验证了NTRS方法的有效性，实验结果表明该方法能缩小链路性能参数的测量规模，降低计算的复杂度。

关键词：性能测量；网络断层扫描；链路消减；系统域网络

1　引言

系统域网络是目前高性能计算机、数据中心的重要组成部分，通过互连将计算节点、存储节点和网络设备整合成为集成服务环境，其中InfiniBand高速互连网络就是一种典型的系统域网络[1]。系统域网络目前已经得到广泛应用，其主要有以下特点：

（1）网络规模日益庞大

系统域网络规模日益庞大，以天河2为例[2]，其互连计算节点数能达到10K以上的量级，而交换节点接近K的量级。数据中心的规模也日益扩大，服务器规模已经达到10K～100K的量级。

（2）相对封闭，集中管理

系统域内的服务节点和网络节点都处于同一管理域内，网络管理者能够全面有效监测整个网络状态，实现对服务节点和网络节点集中的管理控制。

（3）流量行为复杂，拥塞加剧

在高性能计算机集群或者数据中心网络中，传统的MPI（message passing interface）和日益兴起的大数据应用有较强的流量突发性，如常见的栅栏同步many-to-one模式会导致Incast问题，Hadoop会产生all-to-all的流量等。文件系统、虚拟机迁移等应用会产生非常大的数据传输量，给网络带来严重的负载，网络中的流量行为变得日益复杂。

（4）网络故障率指数增加

长期的实践表明，系统故障率随着系统节点数快速增加，N表示节点数，α表示单点可靠性比率，则系统故障率p＝1−αN。例如，从服务节点故障的角度看，若服务单点可靠性为99.99%，按照10K级的规模计算，则系统故障率为63%，若单点可靠性为99.9%，则系统故障率几乎达到100%。

（5）细粒度的网络测量和诊断需求

系统域网络运行的应用通常对网络性能要求严格，需要管理者能更加实时、精确地掌握全网态势和端到端的通信性能，在网络性能下降后及时发现和定位故障和网络拥塞，实现一个快速的故障诊断方案[3]。

因此，对于系统域网络，如何通过有效的测量手段发现网络实时运行状态，当网络发生性能故障时，又如何快速发现并诊断故障，保持和提高网络运行的健壮性，保障网络上关键任务的成功完成非常重要[4]。

网络断层扫描（network tomography，NT）[5]在网络边界上进行端到端的测量，通过测量端到端的通信行为来推断网络内部性能，无需内部网络的协作，从而降低了测量所带来的网络负载，并可实现与被测网络内部结构和协议无关的测量，使得网络断层扫描成为目前主要的网络测量手段之一[6-8]。但是随着系统域网络规模日益庞大，内部链路繁多，使用网络断层扫描技术的测量方法的计算复杂度也随之变大，推测结果的准确性也难以估计。本文通过对实际物理拓扑的策略约束和对链路已知性能信息的挖掘，有效缩小了系统域网络内部链路的规模，降低了网络断层扫描线性数学模型的计算复杂度，保证了网络链路诊断的快速和准确性[9-10]。

本文的主要贡献如下：通过建立多项预处理原则，对实际物理拓扑进行策略约束，充分利用内部链路已知的性能信息，缩小性能测量网络区域和关键链路覆盖等；还能依据测量结果，通过计算链路性能协方差，筛除性能状况较好的链路集合，实现链路数量的有效约简。在此基础上，提出了基于消减策略的网络断层扫描方法，提高了网络链路诊断的准确性，并减少了计算的复杂性。

2　相关研究

基于NT的网络测量技术将网络测量分成两个阶段：（1）数据测量阶段，建立测量模型，在网络边界上采集测量数据，在测量方式上，可以采用主动测量、被动测量或者二者的混合；（2）数据分析阶段，建立统计分析模型，运用统计学理论对测量数据进行分析，推断出网络性能和拓扑。

通过有效的数据测量，获取到端到端的测量数据，建立的数学模型理论上可以是多样的，但在通常情况下，该问题被粗略地近似为线性模型[11-12]。

式（1）中y是端到端测量所得到的数据向量，如丢包率、时延等；A是二进制路由矩阵，表示网络的拓扑结构，A中元素为1时表示测量路径经过某条链路，否则为0；θ代表未知参数向量，对应内部链路级的丢包、时延等；ε表示由θ引入的随机噪声，也可能是测量时附加的噪声。在某些情况下，为了简化，常忽略噪声ε，并用待估参数θ的向量函数X代替式（1）的θ，线性模型变为：

基于式（1）和式（2）的线性模型，推测内部链路级的性能参数可以抽象为：已知路由矩阵A，端到端的测量结果y以及某种合理的噪声分布ε，就可以通过求解线性方程组的方法，解得未知参数向量。

图1所示为由节点组成的树状拓扑，假设节点0为数据包发送端，节点1为网络内部节点，节点2和节点3为数据包的接收端，并记节点0和节点1之间的连接为链路1，同理定义链路2和链路3。为了使用断层扫描技术推测3条链路的丢包率，选择测量路径“0—1—2”和“0—1—3”，记为P1和P2。由节点0向节点2和节点3分别发送探测报文，并测得两条路径端到端的丢包率L1和L2。根据测量路径P1和P2，路由矩阵A可以表示为：

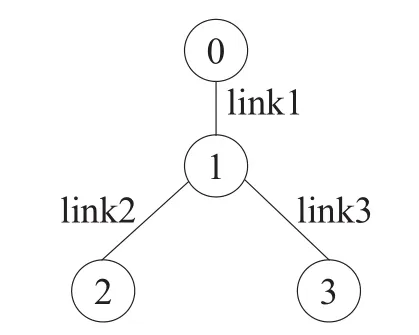
Fig.1 Tree topology of nodes图1　节点组成的树状拓扑图

记3条链路成功率的对数分别为θ1、θ2和θ3，测量路径P1和P2成功率为y1和y2，其中y1＝1−L1，y2＝1−L2，则线性模型为：

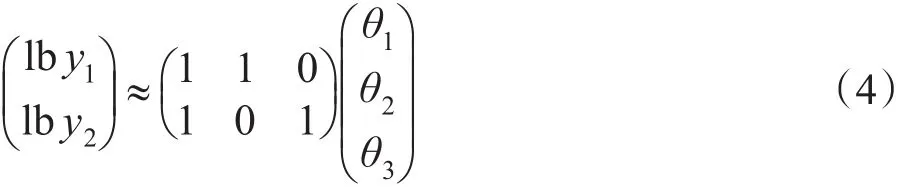
因为路由矩阵A不是满秩的，所以式（4）不存在唯一的解，无法求得3条链路的丢包率。为了获得θ1、θ2和θ3，需要采用一定的方法增加路由矩阵信息，增加端到端的测量数据。如果节点0发往节点2的探测包和节点0发往节点3的探测包之间存在相关性，则可对A和y进行补充。假设y2|3表示同时在节点2、节点3收到的探测报文相对于节点3收到的探测报文的比例，y2|3＝θ2，类似地定义y3|2，则补充后的方程为：

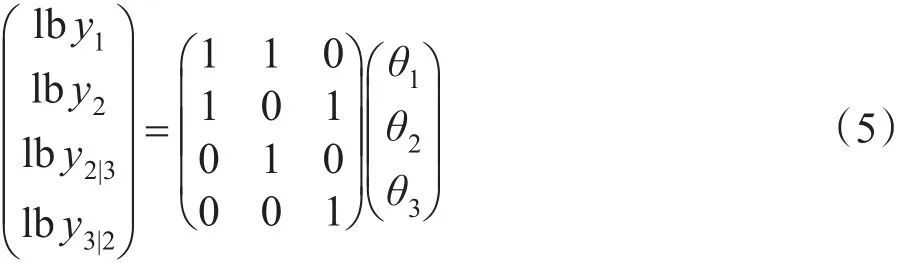
基于两方面的考虑：一是为了达到良好的效率和准确性，所采用的推断分析理论需要在计算复杂度与推断准确性之间保持平衡；二是建立的线性模型存在差异，如噪声ε所服从的分布可能是高斯、泊松、二项式及多项式等其中的任何一种，因此对链路级性能参数的推测即线性模型的求解，采用的推理算法通常有多种，包括极大似然估计法（maximum likelihood estimation，MLE）[13]、期望最大值算法[14]（expectation maximum，EM）、最大概似估计[15]（maximum pseudo likelihood estimation，MPLE）和Bayesian[16]推断方法等。

MINC[17[18]。

在推测链路的丢包率方面，Duffield和Caceres等人依据多播探测包的特点，提出了一种自顶向下的链路丢包率估测方法[19]；Bu等人对网络拓扑进行抽象，提出了基于最小方差加权平均（minimum variance weighted average，MVWA）和基于EM算法的链路丢包率估测方法[20]。

在推测时延方面，Hero和Shih使用有限混合模型对链路时延分布进行建模，提出了一种基于单播测量的链路时延估测方法[21]；针对非平稳网络环境下的链路时延估测，Coates等人提出了基于序贯蒙特卡罗（sequential monte carlo，SMC）的链路时延估测方法[22]。

3　基于消减策略的断层扫描方法

3.1相关定义

对于大规模系统域网络而言，网络内部链路繁多且链接关系复杂，导致所建立的断层扫描线性数学模型规模巨大，不仅使未知链路性能参数的推测复杂度增加，而且使最终的推测性能结果准确率下降。为了清晰准确地描述系统域网络性能测量问题，给出了相关的定义和约束假设。

定义1网络S：由节点和链路构成且任意两节点间存在网络路径，表示为S＝（N，E），其中N＝{H，V}为节点集合，E＝{e0，e1，…}为链路集合，H＝{h0，h1，…}为端节点集合，V＝{v0，v1，…}为中间节点集合。

定义2测量路径pij：表示探测包从源节点hi到目的节点hj所经过的网络路径，记为pij＝（em，…，ek，…，en），其中i≠j，m≠n，ek为测量路径pij上的一条链路。

定义3测量路径集合P：表示参与网络性能测量的测量路径pij的集合，且测量路径集合P的子集表示一次性能测量所涉及的测量路径集合。

定义4路由矩阵Am×n：对于路由矩阵A列向量的维数m，表示参与性能测量的测量路径数量；对于路由矩阵A行向量的维数n，表示参与性能测量的链路数量；对于路由矩阵A第i行第j列的元素aij，取值或为0或为1，表示测量路径pi（pi∈P）是否经过链路ej（ej∈E）。

定义5网络切割：对于网络S，T为预设的较小数值，通常根据经验设置T的数值。假设网络S可以分成n个子网，记为Si（i∈[0，n−1]），且对于任意i，j∈[0，n−1]，Si和Sj（i≠j）之间存在m条链路，链路的平均流量值分别为t1，t2，…，tm，如果有＜T，则网络S可以切割。

3.2拓扑逻辑化原则

在实际的物理网络中，设备之间的链接往往比较复杂，内部链路繁多，如果直接针对其使用断层扫描方法推测网络内部链路的性能参数，工作量巨大，是不现实的，也是没有必要的，而且如果不采取有效的措施，推测结果的准确性会随着问题规模的扩大而逐渐降低。因此，为了增强断层扫描方法实施的可行性，同时也是为了提高推测结果的准确性，针对物理网络的简化即逻辑抽象过程是必不可少的。根据一定的拓扑逻辑化原则，对物理网络的部分链路进行合并或者删除，最终获得性能测量所需要的有效逻辑拓扑。因而，对拓扑逻辑化原则的确定至关重要，直接决定了抽象得到的逻辑拓扑能否反映物理网络的真实性能状况。

原则1合并一致的物理链路。对于物理链路ei和ej，如果有网络设备V将两者连接，并且设备V没有其他物理链路或其他物理链路可以忽略，则称ei和ej为一致的物理链路。同理，一致物理链路的定义也可以推广到多条物理链路。在物理网络的逻辑化抽象过程中，一致的物理链路可以合并成一条逻辑链路，最终获取的性能参数是合并的几条物理链路整体的性能状况。

原则2充分利用内部链路已知的性能信息。对于实际的物理网络拓扑，获取内部链路性能参数的方式有多种。充分利用链路的已知性能信息，对物理网络的部分链路，采用合理的方式提前获取链路的性能参数，使这些链路的性能参数成为已知值，从而减小了未知性能参数的链路数目，降低了断层扫描线性数学模型的求解复杂度。一般可以采用实际测量和参考历史经验值的方法。有些链路容易部署测量工具且所花费的代价较低，此时就可以使用实际测量的方法获取性能参数；有些链路经过多次测量后，发现其性能参数并未发生大的变化，这种情况下就可以以历史经验值作为该链路的性能参数。

原则3缩小性能测量网络区域。对网络进行性能测量的目的是为了及时了解网络的运行状态，发现网络存在的性能瓶颈或故障点。又因为实际的物理网络总是可以划分成多个小网络区域，所以假如某个网络区域已经确定性能状况正常，则测量网络就不需要包括该网络区域。假设在性能测量之前已经确定网络区域性能正常，则对该网络区域中链路无需进行测量，从而缩小了要测量网络的规模。

原则4关键链路覆盖。在实际的物理网络中，内部链路繁多，各条链路在整个网络的运行过程中所发挥的作用也不尽相同，有些链路承载着多个网络区域之间的流量传输，而有些链路只是负责传输其所连端节点的数据，因此不同的链路对网络整体性能状况的影响也不同。在探究网络的整体性能状况时，为了避免测量问题的复杂性，应首先从物理网络中抽象出覆盖关键链路的逻辑拓扑，而对非关键链路暂时不予考虑。在获取关键链路性能参数后，如果确定关键链路无故障，再对非关键链路进行性能测量，此时关键链路的性能参数是已知条件。

针对具体的物理网络，按照上述的拓扑逻辑化原则，能够达到简化测量网络，减小未知性能参数链路的数目，降低断层扫描线性数学模型复杂度的目的。

3.3链路的简约机制

通过物理网络的拓扑逻辑抽象，很大程度上缩小了推断网络内部性能参数的问题规模。但是就所抽象出的逻辑拓扑而言，网络内部链路依然繁多，需要推测的未知性能参数数量仍然很大。为了进一步减少性能参数推测的工作量，降低断层扫描线性数学模型求解的复杂度，继续探究对断层扫描问题简化的方法很有必要。对于网络中的部分链路，其性能参数只是略微偏于正常值，如果将这部分链路的性能参数近似取为正常的历史经验值，就可以增加断层扫描线性数学模型的已知信息，提高推测未知性能参数的效率。

对于网络拓扑N（V，E），其中V和E分别为节点集和边集。如果将边集E分为K和U两部分，其中K为E中已知链路参数的边集，U为E除去K剩余的边集。记Y为端到端的性能测量数据，Au为U中的边在路由矩阵A中所对应的列向量，Ak为K中的边在路由矩阵A中所对应的列向量，Xu为U中的边所对应的未知性能参数，Xk为K中的边所对应的未知性能参数。

因为在建立线性方程组时已经通过采用合适的测量方式使路由矩阵A满秩，且路由矩阵A列向量的减小是随着未知性能参数的减小而进行的，所以矩阵Au必定满秩，上述线性方程组可解，即U中的边所对应的链路性能参数可推测出来。假设网络N在性能测量之前，链路e2表现正常，其性能参数可以近似取历史经验值。如式（6）所示，路由矩阵的第二列表示e2在多条测量路径中的参与情况，θ2表示e2对应的性能参数，如果θ2已知，则可以从路由矩阵中去除e2对应的列向量，从未知性能参数向量中去除θ2，并从测量结果中减去链路e2所影响的部分，式（6）变为如式（7）所示：

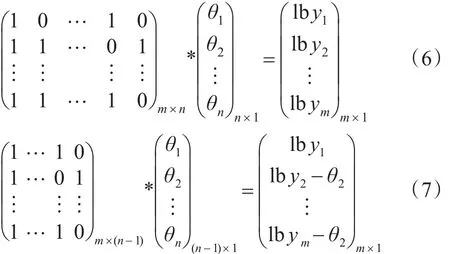
其中路由矩阵的列向量数目减1，未知性能参数的数目减1，测量数据也发生相应变化。

因此，选择合适的K集合较为关键。如果某条链路的性能表现正常，则其性能参数就可以近似取为历史经验值，并可将该链路加入到集合K中。与此同时，集合K中元素数量的选定也同样重要。如果K中元素数量较大，则推测结果会产生很大的误差；如果K中元素数量较小，则不能达到降低问题复杂度的目的。内部链路丢包率或者时延的方差Xk是一个非递减的函数，即链路越拥塞，丢包率或者时延的方差越大，因而可以通过对链路丢包率或者时延方差的排序来选择K集合中的元素。通过对多次端到端性能测量结果（丢包率或者时延）的分析，能够计算出所有链路丢包率的方差或者时延的方差，并可以对这些数据进行排序，得QL＝＜e1，e2，…，en＞。为了选择出集合K中的元素，首先需要确定K集合中元素的数目num（通常是总链路的一定比例），而后从QL队列中选取方差较小的num条链路组成K。从边集E中除去K得到的集合U，就是经过简约处理后实际真正需要推测性能参数的链路集合。

3.4NTRS方法

基于消减策略的断层扫描方法NTRS是在原有断层扫描方法基础上的改进，其主要思想是：首先根据拓扑逻辑化原则，对要测量的目标网络进行抽象并得到对应的逻辑拓扑；其次进行链路简约处理，挖掘链路的已知性能信息，使未知性能参数的链路规模降低，从而建立线性数学模型，并应用一定的推理算法，推测内部链路未知的性能参数。

NTRS方法具体描述如下：

步骤1物理拓扑逻辑化。

假设需要性能测量的物理网络为S（V，E），ei和ej为物理网络S边集E中任意的两条边。从物理拓扑逻辑抽象得到的逻辑网络为S′（V′，E′），ek为物理网络S′边集E′中的一条边。

（1）如果ei和ej为一致性链路，合并ei和ej为ek；

（2）如果S的某条链路ei性能参数可以通过实测或者历史经验值获得，则ei不属于E′；

（3）如果存在某网络区域N（VN，EN），已知N区域网络性能状况正常，则对EN中的链路ei，ei不属于E′；

（4）对于S，如果不存在（1）、（2）和（3）中的任何一种情况，则表示已经获得逻辑拓扑S′。

步骤2逻辑拓扑链路的简约处理。

假设链路简约处理的逻辑拓扑为S′，端到端的性能测量数据为Y，且网络内部链路所需推测的性能参数为丢包率。该步骤主要完成对部分链路性能参数的近似处理，对于丢包率而言，就是寻找丢包率可以近似为0的链路。

（1）通过对多次端到端测量数据的处理，计算每条链路丢包率的协方差；

（2）对链路丢包率的协方差排序，得到一个对应的链路序列Qe；

（3）从Qe链路序列中选取K条丢包率协方差较低的链路，记为＜e1，e2，…，ek＞；

（4）将＜e1，e2，…，ek＞中每条链路的丢包率值近似取为0，则未知丢包率的链路数目减少K。

步骤3推测链路性能参数。

经过步骤1和步骤2，网络断层扫描技术所建立的线性数学模型的复杂度大幅降低，进而对网络内部未知链路性能参数进行推测。

（1）将对网络内部未知性能参数的推测问题分解成若干简单的子问题，即对路由矩阵A进行划分，划分为若干组，每组由一对或多对行向量构成，用S表示所有可能子问题的集合；

（2）针对每个子问题s∈S，建立子线性数学模型Ys＝AsXs；

（3）依据子线性数学模型，得到每个子问题对应的边缘似然函数fs;θs）；

（4）建立似然函数：

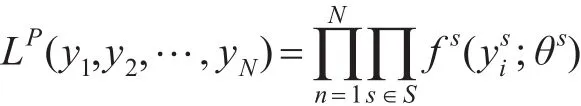
（5）计算对数似然函数的数学期望值，并求解期望值最大时的极值点，得到θ（l＋1）＝Q（θ′，θl）；

（6）设置性能参数θ的初值θ（0），迭代求解θ，直到达到一个稳定值θ。

4　性能分析与评估

假设网络拓扑已知，且在性能测量过程中保持不变。本文实验具体采用的拓扑结构如图2所示，总共由10个节点和9条链路组成，其中1个数据发送节点（节点0），4个中间节点（节点1～4），5个接收节点（节点5～9），不同的链路由其所连接的下端节点号标识。拓扑图中的每个节点都被用来模拟真实网络中不同的设备，节点0和节点5～9用来模拟端设备，节点1～4用来模拟路由器。对于拓扑图中的每个节点都需要设置一定大小的缓冲区，特别是中间节点1～4。通常情况下，在真实网络环境中主要采用两种拥塞避免策略：DropTail和RED（random early detection）。

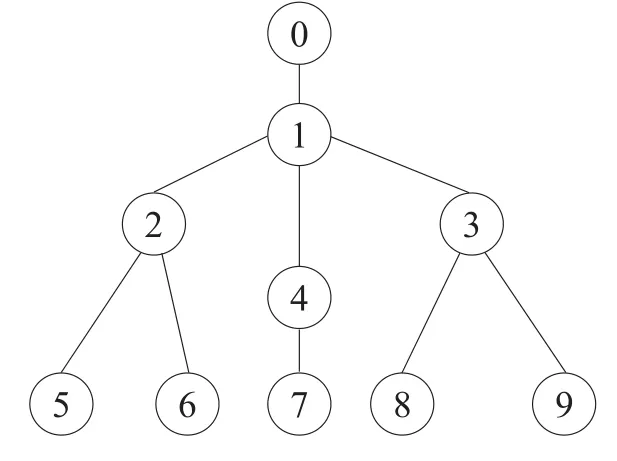
Fig.2 Experimental topology图2　实验拓扑结构图

前者在队列长度达到最大值的情况下，采用丢弃新到分组的策略，而后者随机选择丢弃数据包。在实验中测量流量采用UDP传输，丢包策略选择DropTail方式。如表1所示，对实验拓扑图中的链路属性进行了描述。

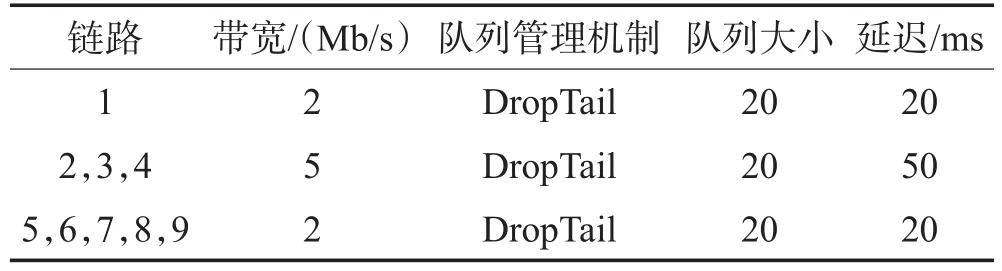
Table 1 Link attributes表1　链路属性

另外，为了使网络中传输合适的数据流量，需要在某些节点上建立相应的协议代理，包括指定端设备的协议绑定及通信业务量模型。TCP流量通过建立TCP代理以及配对的接收代理TCP SINK来实现。UDP流量的实现由UDP代理及接收代理Null配合实现。

仿真实验及分析如下：

根据NTRS方法，对实验拓扑图进行逻辑抽象处理，将链路4和链路7合并为链路47，并假设网络区域A中的链路性能参数（丢包率）可预先测得，则所得逻辑拓扑如图3所示。本实验采取发送组播探测报文的方式进行测量，由节点0作为源节点，其余端节点作为接收节点，并通过TCP生成了背景流量。整个仿真过程持续180 s，测量流量通过UDPAgent发送，每隔30 s进行一次统计，其他链路设置与表1一致。

对于图3中的拓扑，实验将测量得到的统计结果在NS2下采用MPLE算法对链路丢包率进行推测，并通过产生的trace文件计算得到链路实际的丢包率。对于图3中的拓扑，根据测量的统计结果首先计算各条链路丢包率的协方差，并选择协方差最小的一个，将其对应链路的丢包率近似取为0，再在NS2下采用MPLE算法对剩余链路的丢包率进行推测，并分析产生的trace文件，计算得到链路实际的丢包率。图4和图5分别给出在180 s内，链路3和8在不同测量技术下所获得的链路丢包率及真实丢包率的对比图。

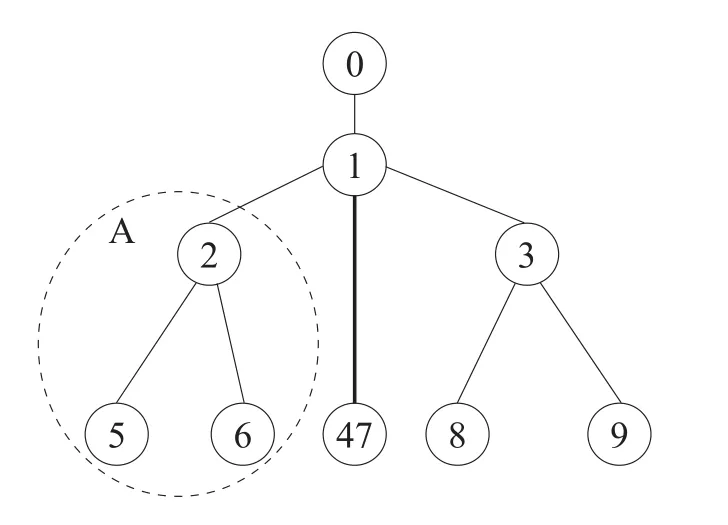
Fig.3 Abstract logical experimental topology map图3　实验拓扑图的逻辑抽象

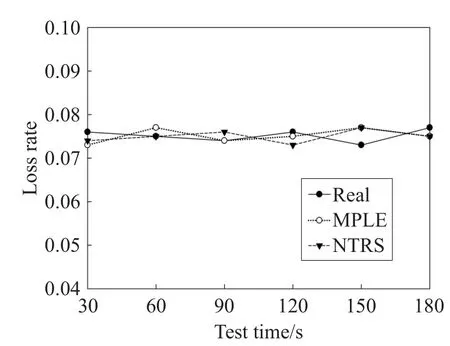
Fig.4 Comparison of three kinds of packet loss rate in Link 3图4　链路3的3种丢包率对比图

从图4和图5可以看出，链路真实的丢包率在7.5%左右，通过NTRS方法推测得到的链路丢包率接近于真实的丢包率，直接使用MPLE算法推测的结果也接近于真实值，因为本实验采取的是组播的测量方式，测量结果相关度高，推测过程引入的误差较小。可以看出，两种方式获取的链路性能参数相近，即拥有同样的测量效果，但是NTRS方法所涉及的未知性能参数明显减少，推测的复杂度也很大程度上得到了降低。通过比较，反映出NTRS方法较直接使用推理算法进行推测的断层扫描方法具有不错的优越性。

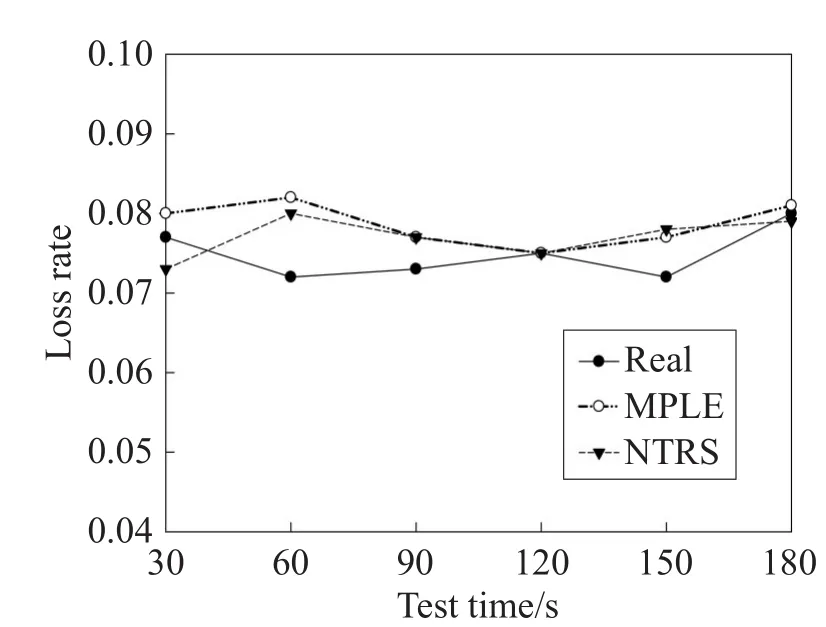
Fig.5 Comparison of three kinds of packet loss rate in Link 8图5　链路8的3种丢包率对比图

实验计算了90 s时各链路的推测丢包率与真实丢包率之间的相对误差，具体如图6所示。通过计算两种不同测量方法所得链路丢包率与真实丢包率之间的相对误差，MPLE方法和NTRS方法虽然都存在误差，但误差都在合理区间内，且两种测量方式有近似的测量效果。NTRS方法通过对实际物理拓扑的逻辑处理以及链路已知性能信息的挖掘，降低了测量链路的数量，进而降低了推测和计算的复杂度，适合于规模较大的网络环境。

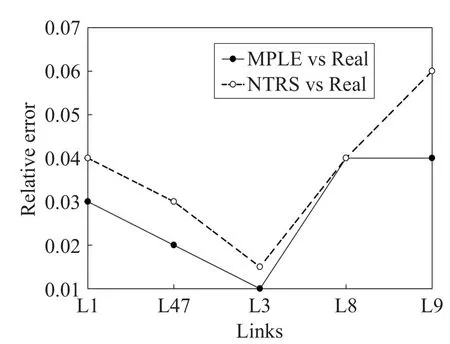
Fig.6　Relative error of packet loss rate in 90 s图6　90 s时各链路丢包率相对误差

5　结束语

本文针对系统域网络趋向于大型化且内部链路繁多的情况，提出了基于消减策略的断层扫描方法NTRS，通过对实际物理拓扑的逻辑处理以及链路已知性能信息的挖掘，缩小了链路性能参数的推测规模，降低了断层扫描线性数学模型的计算复杂度，保证了网络链路诊断的快速和准确性，并通过模拟实验验证了NTRS方法的有效性。

为了提高推测性能参数的高效性，对断层扫描线性数学模型的求解优化也很重要，这部分工作将在下一步进行重点研究。

References:

[1] Infiniband Trade Association. Infiniband architecture specification Volume 1 Release 1.2.1[S]. Nov 2007.

[2] Dongarra J. Visit to the National University for Defense Technology Changsha，China[R/OL].（2013-06-03）[2015-02-12]. http://www.netlib.org/utk/people /JackDongarra/PAPERS/ tianhe-2-dongarra-report.pdf.

[3] Gill P，Jain N，Nagappan N. Understanding network failures in data centers: measurement，analysis，and implications[C]// Proceedings of the 2011 ACM SIGCOMM Conference on Applications，Technologies，Architectures，and Protocols for Computer Communications，Toronto，Canada，Aug 15-19，2011. New York，USA:ACM，2011.

[4] Song H H，Qiu Lili，Zhang Yin. NetQuest: a flexible framework for large-scale network measurement[J]. IEEE/ACM Transactions on Networking，2009，17（1）: 106-119.

[5] Song Tao，Wang Xun，Su Yansen.Anovel approach to identify protein coding domains by sampling binary profiles from genome[J]. Journal of Computational and Theoretical Nanoscience，2014，11（1）: 147-152.

[6] Firooz M H，Roy S. Network tomography via compressed sensing[C]//Proceedings of the 2010 IEEE Global Telecommunications Conference，Miami，USA，Dec 6-10，2010. Piscataway，USA: IEEE，2010: 1-5.

[7] Gu Yu，Jiang Guofei，Singh V，et al. Optimal probing for unicast network delay tomography[C]//Proceedings of the 29th IEEE International Conference on Computer Communications，San Diego，USA，Mar 15-19，2010. Piscataway，USA: IEEE，2010.

[8] Arya V，Duffield N G，Veitch D. Multicast inference of temporal loss characteristics[J]. Performance Evaluation，2007，64（9/12）: 1169-1180.

[9] Zhu Weiping. An efficient loss rate estimator in multicast tomography and its validity[C]//Proceedings of the 3rd IEEE International Conference on Communication Software and Networks，Xi’an，China，May 27-29，2011. Piscataway，USA: IEEE，2011: 90-94.

[10] Adams A，Bu T，Friedman T，et al. The use of end-to-endmulticast measurements for characterizing internal network behavior[J]. IEEE Communications Magazine，2000.

[11] Castro R，Coates M，Liang G，et al. Network tomography: recent developments[J]. Statistical Science，2004，19（3）: 499-517.

[12] MINC: multicast-based inference of network-internal characteristics[EB/OL]. [2015-02-12]. http://gaia.cs.umass.edu/minc/.

[13] Fakhrabadi M，Khani N，Pedrammehr S，et al. Prediction of buckling instability of perfect and defective carbon nanotubes[J]. Journal of Computational and Theoretical Nanoscience，2014，11（11）: 2356-2369.

[14] Shih M F，Hero A O. Unicast-based inference of network link delay distributions with finite mixture models[J]. IEEE Transactions on Signal Processing，2003，51（8）: 2219-2228.

[15] Chua D B，Kolaczyk E D，Crovella M. Efficient monitoring of end-to-end network properties[C]//Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies，Mar 13-17，2005. Piscataway，USA: IEEE，2005: 1701-1711.

[16] Nguyen H X，Thiran P. Network loss inference with second order statistics of end-to-end flows[C]//Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement，San Diego，USA，Oct 24-26，2007. New York，USA: ACM， 2007.

[17] Coates M J，Nowak R D. Network tomography for internal delay estimation[C]//Proceedings of the 2001 IEEE International Conference on Acoustics，Speech，and Signal Processing，Salt Lake City，USA，May 7-11，2001. Piscataway，USA: IEEE，2001: 3409-3412.

[18] Tsang A，Coates M，Nowak R. Passive network tomography using EM algorithms[C]//Proceedings of the 2001 IEEE International Conference on Acoustics，Speech，and Signal Processing，Salt Lake City，USA，May 7-11，2001. Piscataway，USA: IEEE，2001: 1469-1472.

[19] Caceres R，Duffield N G，Horowitz J，et al. Multicast-based inference of network-internal loss characteristics[J]. IEEE Transactions on Information Theory，1999，45（7）: 2462-2480.

[20] Bu T，Duffield N，Presti F L，et al. Network tomography on general topologies.[J]. ACM Sigmetrics Performance Evaluation Review，2002，30（1）: 21-30.

[21] Shih M F，Hero A O I. Unicast-based inference of network link delay distributions with finite mixture models[J]. IEEE Transactions on Signal Processing，2003，51（8）: 2219-2228.

[22] Coates M J，Nowak R D. Sequential Monte Carlo inference of internal delays in nonstationary communication networks[J]. IEEETransactions on Signal Processing，2001，50（2）: 366-376.

HUANG Jie was born in 1976. He received the Ph.D. degree from National University of Defense Technology in 2005. Now he is an associate professor at National University of Defense Technology. His research interests include network measurement and data center network technology，etc.

黄杰（1976—），男，陕西西安人，2005年于国防科学技术大学获得博士学位，现为国防科学技术大学副教授，主要研究领域为网络测量，数据中心网络技术等。发表学术论文20多篇，承担国家自然科学基金项目1项、湖南省自然科学基金项目1项。

CHEN Lin was born in 1976. She received the Ph.D. degree from National University of Defense Technology in 2005. Now she is an associate professor at National University of Defense Technology. Her research interest is data center network resource management technology.

陈琳（1976—），女，福建陇海人，2005年于国防科学技术大学获得博士学位，现为国防科学技术大学副教授，主要研究领域为数据中心网络资源管理。发表学术论文20多篇，主持湖南省自然科学基金项目1项、承担国家自然科学基金项目1项。

WANG Binfeng was born in 1989. He is a Ph.D. candidate at National University of Defense Technology. His research interest is data center network resource management technology.

王斌锋（1989—），男，陕西宝鸡人，国防科学技术大学博士研究生，主要研究领域为数据中心网络资源管理。

Network Tomography Based on Reduction Strategy in System Area Network*

HUANG Jie＋，CHEN Lin，WANG Binfeng
School of Computer，National University of Defense Technology，Changsha 410073，China ＋Corresponding author: E-mail: agnes_nudt@qq.com

HUANG Jie，CHEN Lin，WANG Binfeng. Network tomography based on reduction strategy in system area network. Journal of Frontiers of Computer Science and Technology，2016，10（1）：65-73.

Abstract:System area network is the important component of high performance computer and data center. The current system area network has the characteristics of larger-scale network，more internal links，more complex behavior of network traffic，higher sensitivity of applications on network performance and so on. Those problems cause that the computational complexity of the performance measurement is exponential growth of the traditional network tomography. To address this problem，this paper proposes a new method of network tomography called NTRS（network tomography based on reduction strategy）. This method proposes a number of pre-treatment principles to optimize the measurement topology and these principles include merging the consistent physical links，making full use of the known performance information of internal links，narrowing the scope of the performance measuring area and covering the key links. According to the results of measurement，this method screens for link collection with better performance to achieve an effective reduction of the measuring links through computing the covariance of performance parameters for internal links in light of end-to-end performance measurement data. And the method largely improves the accuracy of performance measurement and the link diagnosis speed. Finally，this paper validates the effectiveness of NTRS by simulation，the results show that NTRS can decrease the number of the link performance parameters needed to measure and reduce the computational complexity.

Key words:performance measurement; network tomography; link reduction; system area network

文献标志码：A

中图分类号：TN915

doi:10.3778/j.issn.1673-9418.1505012