基于模糊综合评价法的跨境电子商务物流中心选址研究

穆 杨

北京物资学院

基于模糊综合评价法的跨境电子商务物流中心选址研究

穆 杨

北京物资学院

信息产业与互联网技术的飞速发展扩大了商品的流动范围，经济的发展与人均收入水平的提高也大大促进了人们的购买力。海淘族的增加使一些电商看到了商机，未了更好的促进跨境电子商务的发展，建立海外仓库势在必行。通过对我国跨境电商物流中心选址问题的研究，构造了物流中心选址模型，运用AHP和模糊综合评价法相结合的方法，结合实例，验证了此方法的可行性。

跨境电子商务；物流中心；AHP；模糊综合分析法；选址

一、背景

随着我国经济的发展与人均可支配收入的提高，在贸易的全球化这一背景下，我国跨境电子商务发展迅速。对于跨境电子商务而言，物流是最核心的内容，设立海外仓储，既解决了货损大、易丢失的缺点，又可以让商家直接在网上管理海外仓储，商家可以直接在网上指令海外仓储对货物进行存储、分拣、包装、配送，及时更新并显示库存状况等。[1]

二、跨境电子商务物流中心选址问题

(一)跨境电子商务物流中心选址

1.选址原则

由于跨境电子商务物流中心涉及到厂房的建社和大量的设备购买，如果选址不当，将会造成巨大的浪费，因此，选址应遵循以下原则：①适应性原则；②协调性原则；③经济性原则；④战略性原则。[2]

2.选址因素

本文主要选择的因素有：自然环境、交通运输、经营环境、候选地、公共设施。[3]

图1 物流中心选址层次关系模型

3.选址方法

本文选用模糊综合评价法对跨境电子商务物流中心进行选址。综合模糊评价法是在模糊环境下，考虑多种因素的影响，为了某种目的对一事物做出综合据侧的方法。它的特点在于，评判逐对象进行，对被评价对象有唯一的评价值，不受被评价对象所处对象集合的影响。

三、跨境电子商务环境下物流中心选址模糊评价模型构建

(一)确定评价因素和等级

设U={μ1, μ2, μ3, …, μm}为刻画被评价对象的m种因素(即评价指标)，V={υ1, υ2, …υn}为刻画每一因素所处的状态的n种决断(即评价等级)，m为评价因素的个数，由具体指标体系决定，n为评语的个数，一般划分为3～5等级。

(二)确定权重

本文运用层次分析法确定权重

1.构造判断矩阵

用A、B、C分别代表第一层级，第二层级，第三层级，各层级之间的因素可以两两比较。假设A中有m个元素，那么可以通过两两比较得出判断矩阵A=(Bij)m×m，Bij表示因素Bi和因素Bj比较相对于目标的重要值。构造的判断矩阵为：

矩阵A有如下性质：

(1) Bij＞0

(2) Bij=1/ Bji(i≠j)

(3) Bii=1 (I，j=1，2，…m)

在层次分析法中，为了使决策判断定量化，形成上述数值判断矩阵，常根据一定的比率标度将判断定量化(见图2)。

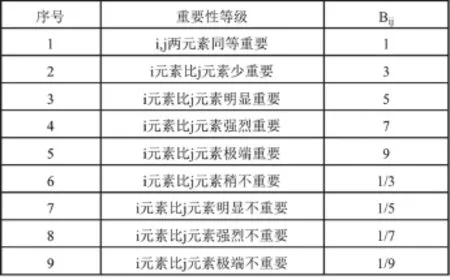
图2 判断矩阵标度及其含义

注：Bij={2，4，6，8，1/2，1/4，1/6，1/8}表示重要性等级介于Bij={1，3，5，7，9，1/3，1/5，1/7，1/9}，这些数字是人们根据定性分析的感觉主管定性的。

2.判断矩阵的一致性检验

实际问题建立起来的判断矩阵往往满足不了一致性，为了保证应用层次分析法分析得到的理论合理，需对构造的判断矩阵进行一致性检验。

(1)求出矩阵A的特征值λ，λ满足公式Ax=λx。对于所有aii=1，有：

当矩阵具有完全一致性时，λ1=λmax=n，其余特征值均为零；而当矩阵A不具有完全一致性时，则有λ1=λmax＞n，其余特征值的关系为：

算出判断矩阵偏离一致性的指标CI：

CI值越大，判断矩阵偏离完全一致性的程度越大；CI值越小，判断矩阵的一致性越好。

(2)求得随机一致性比率CR

1～9阶的判断矩阵的RI值如下表：

表1 平均随机一致性指标

当阶数大于2时，计算CR，公式如下：

当CI＜0.10时，即认为判断矩阵具有满意一致性。

3.确定各层因素的权重

一致性检验通过后，通过对各层因素指标的分析，求得个评价指标的权重系数。

(三)评价矩阵的构建

在确定了评价因素和等级后，对评价目标中每个因素集 Ui进行量化，确定每一个单因素中评价目标对模糊子集的隶属度，进而得到模糊关系矩阵：

R=(rij)m×n

(四)进行模糊合成

进行各级综合模糊评价，设U中各指标因素所对应的权重为Wij用Wi代表第二级指标的权重，Wi={Wi1, Wi2, …, Wij}，二级综合评价向量：Hi=Wi×R (5)

用W代表第一级指标的权重，W={W1, W2, …, Wi}，一级综合评价向量：Ii=W×Hi(6)

层次多的以此类推。

(五)计算各个评判对象的综合值

将评语集 v={v1, v2, …, vn}对应的结果赋予一定的值 V={V1, V2, …, Vn}，综合分值为：E=V×Ci。然后按照分值的大小，就可以选出最合适的物流中心地址。

四、实证分析

一跨国物流电商企业准备在某地建设海外仓库，现有3个地址比较合适，现用综合模糊分析法对3个地址做出评价，用L、M、N表示3个地方。

(一)确定权重

在本文的第二节已经构造出了选择物流中心的层次分析图，现在用AHP法确定各要素的权重。

1.构造判断矩阵

采用Delphi法，得出的各层的比较矩阵为：

2.判断矩阵的一致性检验

矩阵的λ可以用Matlab求出，经Matlab计算可知：矩阵A的λmax=5，CI=0，RI=1.12，CR=0＜0.10，矩阵具有满意的一致性；矩阵B1的λmax=4，CI=0，RI=0.90，CR=0＜0.10，矩阵具有满意的一致性；矩阵B4的λmax=4，CI=0，RI=0.90，CR=0＜0.10，矩阵具有满意的一致性；矩阵B5的λmax=4，CI=0，RI=0.90，CR=0＜0.10，矩阵具有满意的一致性；矩阵C9λmax=3，CI=0，RI=0.58，CR=0＜0.10，矩阵具有满意的一致性；矩阵C10为2阶矩阵，所以矩阵具有满意的一致性。

3.各层因素的权重

用矩阵中每一行中的数值相加和除以行列式中所有数值的总和，即为每一行代表的因素的权重。通过计算得知：

WA=(0.097，0.188，0.340，0.187，0.187)

WB1=(0.25，0.25，0.25，0.25)，

WB4=(0.1，0.1，0.4，0.4)，

WB5=(0.417，0.301，0.185，0.097)

WC9=(0.333，0.333，0.333)，

WC10=(0.5，0.5)。

(二)模糊评判

采用德尔菲法，得出3个地区的模糊综合评判如下图：

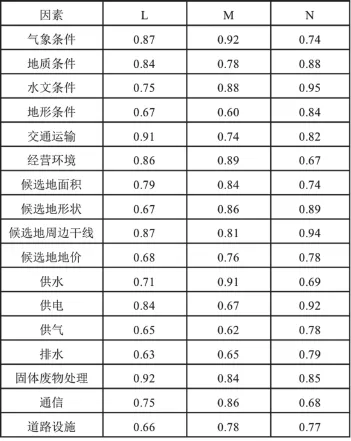
图3 各地模糊综合评判表

(三)综合评判

由表3可知：

三 级 综 合 模 糊 评 价 为：JC9= WC9×RC9=(0.7326，0.7326，0.79587)，JC10=(0.775，0.745，0.82)，由此可以得出：

二级综合模糊评价为：HB1=WB1×RB1=(0.7825，0.795，0.8525)，HB4=WB4×RB4=(0.766，0.798，0.851)，HB5=WB5×RB5=(0.7415，0.7645，0.7792)，所以：

级综合模糊评价为：A=WA×RA=(0.821，0.811，0.770)

综上所述，3块候选地的综合排序为：L、M、N，L地的得分最高，所以L最适合做物流中心。

五、结论

本文结合了跨境电子商务这一热点问题，研究了跨境电商物流中心的选址问题，通过模型的构造，分析了选址中存在的一些问题，综合运用AHP法和模糊综合分析法对此模型进行验证。通过实证分析，验证了此种方法的可行性，证明了此种方法具有一定的实用意义。但是在现实中，选址可能会受到其他方面的影响，此模型与方法还有待改进。

[1]张宝明，周沛锋，孟玲.电子商务下配送中心选址研究.物流科技[J] .2014，10：55页.

[2]李振宇. 基于 GIS 的连锁店空间布局模型分析 [J] .物流科技，2004 (5)：56-58.

[3]杜栋，庞庆华等.现代综合评价方法与案例精选[M].北京：清华大学出版社，2008.

穆杨(1991-)，女，回族，安徽宿州市人，研究生，单位：北京物资学院，研究方向：物流评价