基于垂直平分线的非测距定位算法

邹东尧，李　晨，刘碧微

(郑州轻工业学院 计算机与通信工程学院，郑州　450001)



基于垂直平分线的非测距定位算法

邹东尧，李晨，刘碧微

(郑州轻工业学院 计算机与通信工程学院，郑州450001)

摘要：在无线传感器网络定位机制中，近似三角形内点测试(APIT)定位算法因思想简单、硬件成本低、定位精度高而被广泛应用，但算法性能会因锚节点分布不均匀受到严重影响；为提高节点定位精度和解决APIT定位算法边缘效应的问题，提出一种基于垂直平分线的非测距定位算法；该算法利用接收信号强度指示值(RSSI)值筛选锚节点并与等腰三角形底边中垂线过顶点的几何原理结合进行定位，可以得到比较合理的定理精度，性能相对稳定；仿真结果表明，该算法可有效提高无线传感器网络定位的精度和覆盖率。

关键词：无线传感器网络；近似三角形内点测试；接收信号强度指示； 定位精度；定位覆盖率

0引言

无线传感器网络(wireless sensor networks，WSNs)中节点的位置信息至关重要。对于无线传感器网络中所得到的感知数据，没有相应的位置信息，通常是无意义的[1-2]。实时地确定事件发生的位置也是提供安全反恐、国防军事、环境监测与预报位置信息的前提，所以定位技术对有效应用无线传感器网络起着关键作用[3-5]。

根据定位过程中是否依靠测量实际节点间的距离，定位算法可分为基于测距和基于非测距两种。基于测距的定位算法主要有AOA、TOA、TDOA、RSSI[6-7]；基于非测距的定位算法主要有质心算法、DV-hop算法、Amorphous算法、APIT算法[8-13]。基于测距的定位技术比基于非测距的定位技术精确度更优，但测距过程在一定程度上加大了通信量和计算量，也会使硬件成本增加。因此，基于测距的定位技术在大规模传感器网络中受到限制，而基于非测距的定位技术硬件成本合理，能耗低，适用范围比较广泛，但定位精度较低。APIT定位算法是经典的无需测距的定位算法之一，该算法在密集网络中,定位精度较为合理, 性能相对稳定, 网络成本低, 实现也相对容易。但在随机分布网络中会造成定位误差较大、覆盖率较低的现象。

为了提高定位的精度和覆盖率，本文提出了一种基于垂直平分线的非测距定位算法(perpendicular bisector algorithm，PB算法)。该算法只需提取接收到的RSSI值，且不需要将其转化为具体的距离值，减小了计算复杂度,并且对锚节点分布的方向没有要求，因此提高了定位精度、解决了边缘节点无法定位的问题。

1APIT算法存在的问题

APIT算法是一种适用于大规模无线传感器网络的分布式非测距定位算法。该算法原理是首先从未知节点周围选取3个锚节点组成一个三角形，若未知节点在三角形内部，则将其标记，按照相同原理对未知节点周围的锚节点进行不同组合组成不同三角形，并分别标记[14]。最终计算出所标记的所有三角形的重叠区域，求其质心位置即为定位结果。APIT定位算法存在的问题如下：

1)APIT定位算法只有在锚节点数量足够多时，才可将未知节点完全覆盖到锚节点构成的三角形区域中。但由于WSNs的节点是随机部署的，可能出现因某些区域分布不均匀而导致部分节点无法定位的现象，并且影响定位精度。

2)在WSNs中某些小区域内因未知节点的邻居锚节点个数量少于3个无法构成三角形进行定位，从而形成未确定节点。当未知节点不在邻居锚节点所构成的三角形内也会成为未确定节点。

3)APIT定位算法由质心计算公式得出重叠部分的质心位置，但是由公式所得到的质心位置不是节点的准确位置，所以会造成一定的误差。

4)通常会采用增加锚节点数量的方法解决APIT 定位过程出现的 OutToIn或InToOut问题。然而锚节点数量的增加会使整个网络的能量消耗及成本增多。

2PB算法

2.1算法描述

锚节点向周围节点广播自己的ID编号、位置信息、发射信号强度，未知节点接收通信半径内锚节点的广播信息并计算接收到的RSSI值。未知节点根据设定的阀值RSSIf，选取其接收的RSSI值中所有大于RSSIf的锚节点。

如图1所示，选择RSSI数值相差小的两组锚节点，RSSI值相差小即锚节点与未知节点距离接近。例如P1和P2，P3和P4，分别连接P1和P2得线段c1，连接P3和P4得线段c2，线段c1和c2即表示为两个等腰三角形的底边。分别作两个三角形底边c1和c2的垂直平分线l1和l2，设两条垂直平分线相交于点P，根据垂直平分线定理可知，点P即为未知节点的定位坐标。

图1　PB定位算法

由于最终的定位结果是通过计算垂直平分线l1和l2的交点所得，所以当底边不合适时，对定位的结果影响较大，甚至会导致无法定位。例如若直线l1和l2平行则无法计算出定位坐标。如图2所示，此时l1和l2相交于无穷远处，即使两直线不平行，斜率相近也会造成误差的较大。

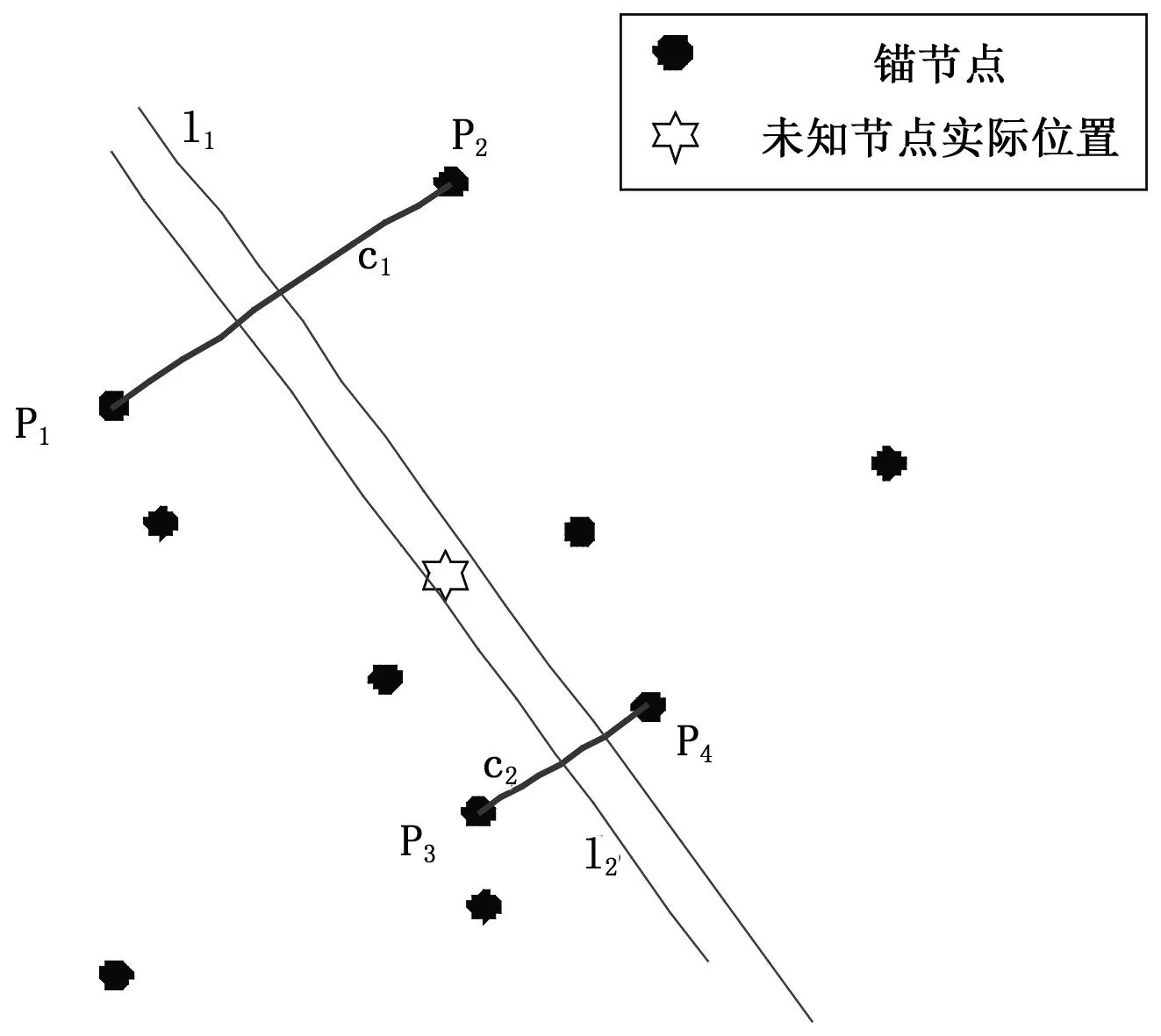
图2　垂直平分线平行

此外若选取的锚节点过近，如图3所示，此时的线段P1P和P2P长度差距不大，但由于锚节点P1和P2相距过近使得偏差严重扩大，导致定位结果误差过大。因此，选取锚节点时对应的垂直平分线不能平行，还要限制选取锚节点间的距离，避免过近而造成较大的定位误差。

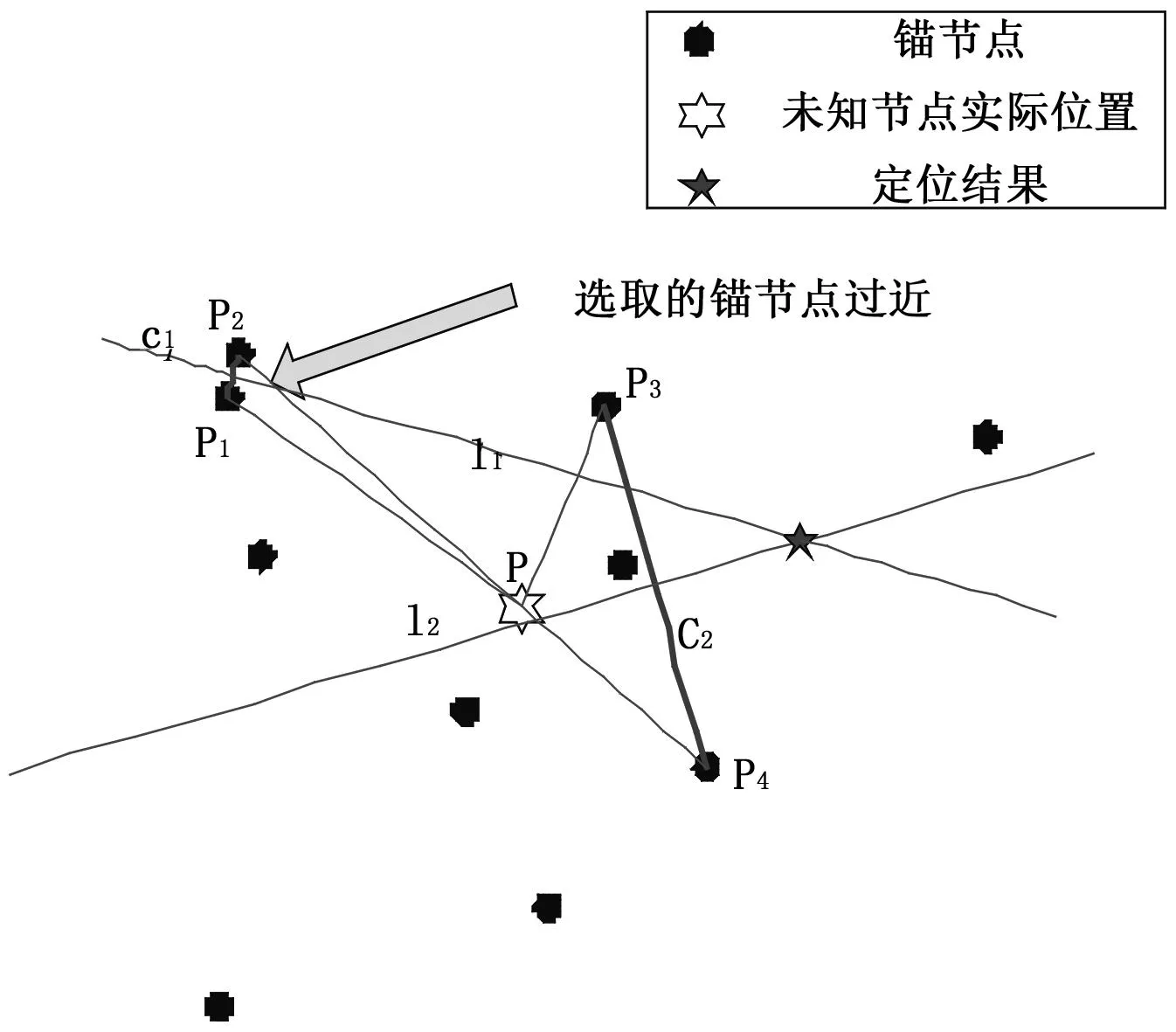
图3　锚节点距离过近

设选定的锚节点坐标P1(x1,y1)，P2(x2,y2)，P3(x3,y3)，P4(x4,y4)，为防止底边平行而无法定位，建立限制条件：

(1)

为避免图3所示的底边过短情况的出现，建立限制条件：

(2)

2.2算法步骤

2.2.1提取信息

各锚节点向周围节点广播自己的位置信息，未知节点接收其通信半径内或RSSI值大于阀值的锚节点信息，将锚节点的RSSI值和坐标放入矩阵S，如公式(3)，其中锚节点Pi(xi,yi)的RSSI值为Si，矩阵S第一行为锚节点的RSSI值，第二行第三行为对应锚节点的横纵坐标。设接收到附近N个锚节点的RSSI数据，那么矩阵S为三行N列矩阵：

(3)

其中:Si≥RSSIf(i=0,1,2，...，N-1)。

2.2.2整理锚节点信息矩阵

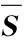
(4)

2.2.3除去不符合条件的锚节点

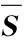
2.2.4连接符合条件的锚节点和未知节点组成三角形，并作以两个锚节点为底边的垂直平分线，垂线的交点为定位结果。

首先选取矩阵SS的前两列，既相对差距最小且符合条件的两组锚节点，会得到3个或4个锚节点。设有4个锚节点P1(x1,y1)，P2(x2,y2)，P3(x3,y3)，P4(x4,y4)。将P1和P2相连得到直线l1，P3和P4相连得到直线l2，l1和l2垂直平分线的焦点为未知节点定位结果。

3算法仿真与分析

3.1锚节点最小距离

在1.1节算法描述部分，提到为了控制算法误差，设定了锚节点的最小距离参数dF。表示在选定到未知节点距离相同或相近的锚节点时，两个锚节点的最小距离不能小于dF。为了分析参数dF的变化对定位精度的影响，仿真环境设置为100 m×100 m的方形区域，节点通信半径为10 m，节点总数为400个，锚节点数量占节点总数的20%、22.5%、25%……50%递增变化，每种情况测试10次，最终结果取其均值以减少误差，则dF在(0,12]内取值时，平均误差如图4所示。

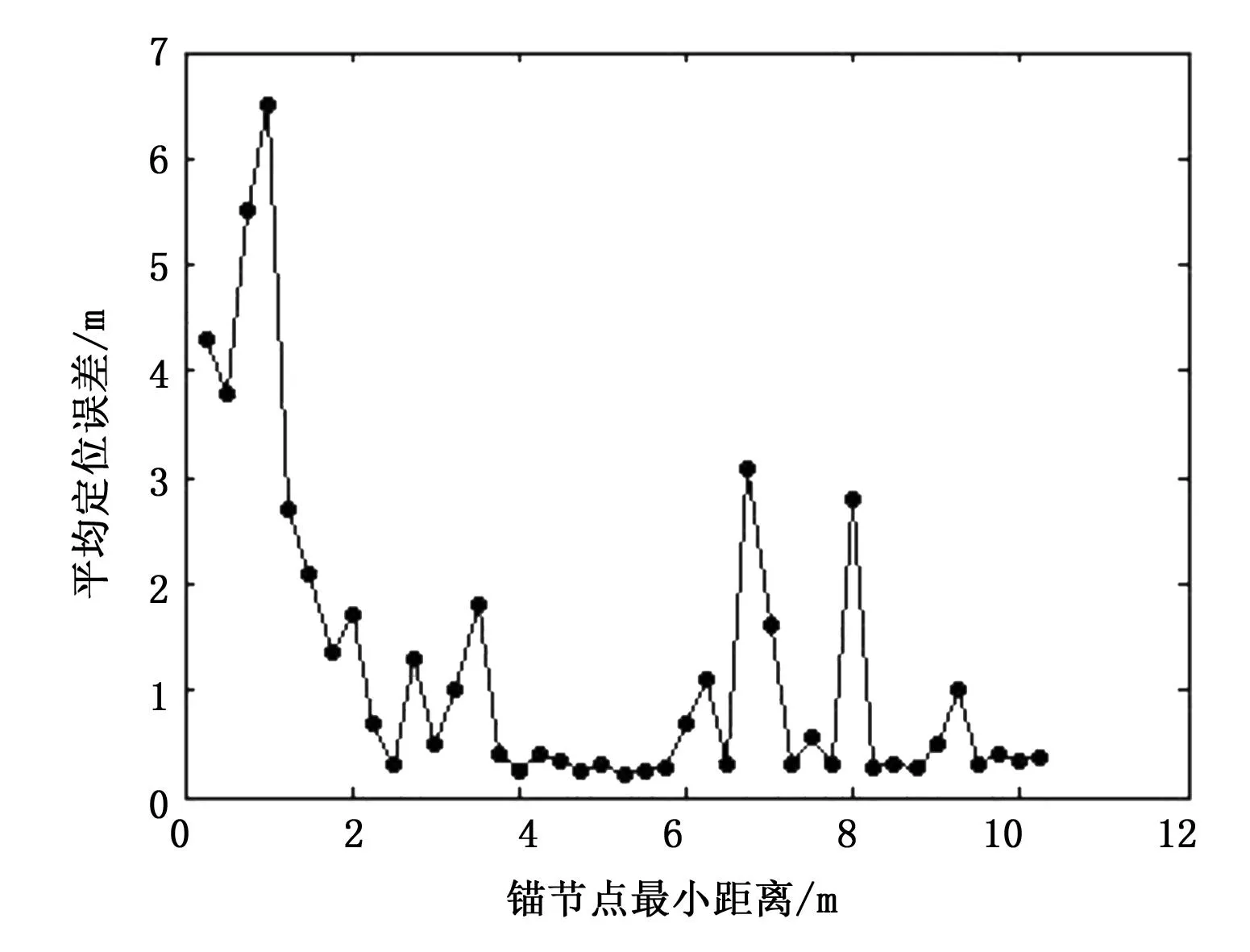
图4　dF与平均定位误差关系图

由图4可以看出，当dF小于2 m时定位误差非常大，此时会出现图3中的锚节点过近而造成的定位偏离。此现象可以通过直线的斜率公式解释，设直线AB上两点A(x1,y1)，B(x2,y2)，若直线的斜率存在则可以表示为k= (y1-y2)/ (x1-x2)。点A和B比较接近时可以表示为：y1≈y2，x1≈x2。那么y1-y2或x1-x2有很小的变动都会导致斜率k的较大变化，此时误差会得到进一步扩大。因此限制所选取的锚节点距离有其必要性。

当dF大于10.25 m时，由于dF过大，满足条件的锚节点不足以满足定位需求而无法定位，出现图4中所示的后段无数据情况。当dF取值过小时，因垂直平分线可能偏离严重而造成误差较大，dF取值过大时，因符合条件的锚节点过少而无法定位。而在4 ~6 m的取值范围内取值时，平均误差较小且变化幅度不大。因此，取4 ~6 m之间平均误差最小的点为最优dF值，即dF=5.25 m。

3.2定位精度和覆盖率

节点定位精度和覆盖率是评价一个定位算法性能好坏的关键指标[15]。在实验过程中，我们利用随机生成的场景进行仿真实验，比较两个算法在相同实验条件下的定位精度和覆盖率。在100 m×100 m的方形区域进行测试，节点通信半径为10 m，节点总数为400个，每种情况测试10次得到相应数据，取其均值为最终结果。APIT算法和PB算法定位误差如图5所示。

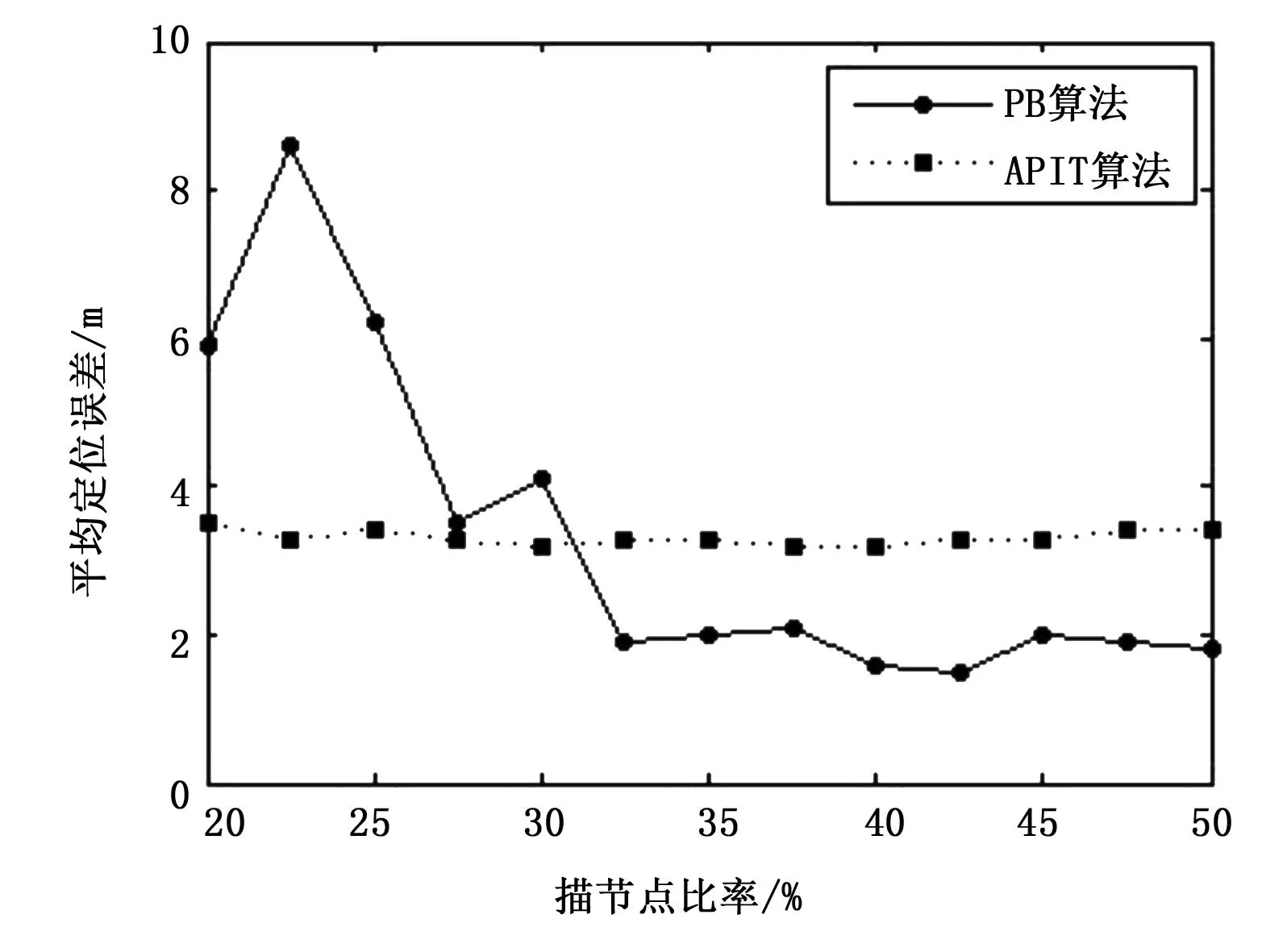
图5　PB算法与APIT算法定位误差比较

由图5可以看出，当锚节点数量达到32.5%时，PB算法的定位误差趋于一个定值，其定位误差低于APIT算法。在锚节点密度较低时，很多未知节点不能收到足够多的锚节点信息，因此APIT算法不能对此类节点进行定位，而PB算法可以对此类节点进行定位，但由于此类节点收到的锚节点信息较少，所以定对位误差较大，使PB算法整体定位误差提高。APIT算法和PB算法定位覆盖率如图6所示。

图6　定位覆盖率比较图

由于无线传感器网络中节点的随机分布特点，导致了节点分布不均匀和边缘效应情况的出现。使用APIT算法定位会存在一些无法定位的节点，定位覆盖率也会随之下降。从图6中可以看出，两种算法随着锚节点比例的增加定位覆盖率都有所增加。由于PB算法只需根据锚节点建立两条直线，解出两条直线的垂直平分线交点即可，所以定位覆盖率要高于APIT算法。

采用PB算法进行定位，定位精度和覆盖率均优于APIT算法。此外在组网阶段，PB算法不需要进行网格划分，形成网格阵列，从而降低了组网过程的复杂度。定位过程中APIT算法要进行多次区域划分，寻找重叠区域，该过程计算量大对硬件要求较高，而PB算法只需根据锚节点建立两条直线求其垂直平分线的交点，减少了计算难度。

4结束语

本文提出了一种基于垂直平分线的非测距定位算法，利用RSSI值筛选锚节点并根据等腰三角形底边中垂线过顶点的几何原理进行定位，解决了APIT算法中锚节点分布不均匀定位误差大和边缘效应的问题。实验结果表明：在组网复杂性、计算难度、定位精度和覆盖率方面，PB算法相比APIT算法均有所改善。

参考文献：

[1] 杜杨洋,毛永毅.基于多功率移动锚节点WSN 智能定位算法[J].电子技术应用, 2015,41(6):88-90,94.

[2] 王焱,单欣欣,姜伟.无线传感网络中移动节点定位技术研究[J].传感技术学报,2011,24(9):1326-1330.

[3] 史跃飞,冯秀芳,高昊.一种基于动态锚节点的改进加权定位算法[J].计算机应用与软件,2013,30(10):151-154.

[4] 毛科技,金洪波,苗春雨，等.无线传感器网络中的节点位置验证方法[J].传感技术学报,2015,28(6):850-857.

[5] 周帆,江维,李树全，等.基于粒子滤波的移动物体定位和追踪算法[J].软件学报, 2013,24(9):2196-2213.

[6] 邹东尧,郑道理,李晨.RSSI曲线拟合的误差分析与分段方法[J].郑州轻工业学院学报(自然科学版),2014,29(2):62-66.

[7] 何中胜,朱宇光,庄燕滨.无线传感器网络中覆盖控制技术综述[J].计算机测量与控制,2012,20(7):1737-1739,1749.

[8] Nieolescu D, Nath B. Ad Hoc positioning systems(APS)[A].Global Telecommunications Conference[C].San Antonio,2001:2926-2931.

[9] Bulusu N, Heidemann J, Estrin D.GPS-less low cost outdoor localization for very small devices[J].IEEE Personal Communications Magazine,2000,7(5) :28-34.

[10] Rout C S, Krishna S H, Vivekchand S R C. Hydrogen and ethanol sensors based on ZoO nano wires and natotubes[J].Chemical Physics Letter,2006.

[11] 黄海辉,李龙连.WSN 中一种基于RSSI 的移动节点改进定位算法[J].电子技术应用,2015,41(1):86-89.

[12] 高洪波,廖明潮.一种改进的DV-HOP 算法在WSN 中的定位研究[J].科技通报,2014,30(9):160-166.

[13] 巩丽涛.无线传感网络中的节点定位算法研究[D]. 无锡:江南大学,2013.

[14] 黄小瑛.基于近似三角形内点测试(APIT)的无线传感器网络节点定位技术研究[D].太原:太原理工大学,2010.

[15] 熊茂华,熊昕.无线传感器网络技术与应用[M].西安:西安电子科技大学出版社,2014.

A Non-distance Localization Algorithm Based on Perpendicular Bisector

Zou Dongyao, Li Chen, Liu Biwei

(College of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou450001,China)

Abstract:In wireless sensor network positioning schemes, APIT is widely used because it is easy, entails low hardware cost and provides high positioning accuracy. But its algorithm performance is severely affected by uneven distribution of anchors. A non-distance localization algorithm based on perpendicular bisector is proposed to improve node positioning accuracy and solve the edge effect problem of APIT. The proposed algorithm selects anchors using RSSI values and fixes the position by combining with the geometrical principle that the mid perpendicular of the base line in the isosceles triangle passes the vertex. The positioning accuracy is enhanced in this way and the stable performance is achieved. Simulation results show that the proposed algorithm can effectively improve positioning accuracy and coverage of the wireless sensor network.

Keywords:wireless sensor networks(WSNs); APIT; RSSI; positioning accuracy; localization coverage

文章编号：1671-4598(2016)02-0202-03

DOI：10.16526/j.cnki.11-4762/tp.2016.02.056

中图分类号：TP393

文献标识码：A

作者简介：邹东尧(1973-)，男，河南许昌人，博士，副教授，主要从事物联网信息感知、无线传感器节点定位技术方向的研究。

基金项目：河南省科技厅科技攻关项目(112102210321)；河南省产学研合作项目(122107000022)；2014年郑州轻工业学院研究生创新基金项目。

收稿日期：2015-08-21；修回日期：2015-08-29。