网络控制系统H∞指数稳定容错控制器的设计

张　鹏，宫占霞

(哈尔滨理工大学 自动化学院，哈尔滨　150080)



网络控制系统H∞指数稳定容错控制器的设计

张鹏，宫占霞

(哈尔滨理工大学 自动化学院，哈尔滨150080)

摘要：随着网络控制系统的广泛应用，容错控制问题也成为了大家研究的重点，尽管网络控制系统的容错控制方法很多，但是还有一些方法被忽略，为了更好地实现容错控制，提出一种设计，针对一类时延网络控制系统(NCS)，在执行器出现故障为乘性故障情况下，对系统建立离散形式的数学模型，运用离散系统的有界实引理，设计此系统的H∞指数稳定容错控制器；最终通过LMI工具箱求出状态反馈矩阵，获得设计的容错控制器;数据示例证明了此控制器符合设计要求，并且能够实现容错控制。

关键词：网络控制系统；乘性故障；容错控制器；指数稳定

0引言

网络控制系统(NCS)涵盖了通信技术、网络技术、控制技术、信息技术和计算机等技术，给企业管理和工业控制等方面提供了一种崭新的模式。网络控制系统中,基于公用的网络控制平台，控制信号和系统信息传输于控制部件间。传统的控制系统是以点与点之间互联实现的，相比之下，网络控制系统的模块化设计更便捷，实现更简单，维护更方便；远程控制与操作、资源共享也均实现；还有易扩展、成本低等优点。同时，由于网路带宽的有限性，在传输中，数据包避免不了会出现排队等待、碰撞、重传现象等等；网络的数据通道自身带有连接中断和网络拥塞等现象；数据在传输过程中会经过很多通信设备和计算机，数据会通过不同路由来选择路径。因此，由于网络媒体的介入，使时延与数据丢包、时序错乱等现象普遍存在，使得对NCS的分析与控制更为困难。

目前，现代系统复杂化、大规模化的发展方向已经成为趋势，正因为这样的发展趋势使得现代系统存在一定的缺点，一旦出现故障，就可能危及到人员和财产的安全，并造成巨大损失。因此，控制系统必须拥有高可靠性。在工业控制过程中，系统的传感器或者执行器等器件均有出现故障的可能性，当故障出现，系统还可以稳定地运行，这就是容错控制的功能。容错控制技术即让系统具有一定容错能力来让系统应对突发故障，即系统中的部分器件突发故障，系统仍然保持稳定，在原有的性能或者在可接受的一定性能范围内完成要求的控制任务。因此，随着NCS结构的逐渐复杂化，在稳定性这一性能方面要求的提高，容错控制为NCS创新出及其有利的解决突发故障的方法。

目前，NCS系统中涉及到的有关容错控制的课题越来越多。文献[1]使用Lyapunov函数和线性矩阵不等式设计了γ次优鲁棒H∞反馈容错控制器；文献[2]针对风能转换系统执行器出现故障等问题，分析建立了该系统的数学模型，使用状态反馈并行分布补偿结构设计出风能转换系统的一种在执行器突发故障时的鲁棒容错控制器；文献[3]针对航空工具的发动机突发故障问题，使用配置特征结构的方法，不仅配置极点，还配置特征向量，然后调节以使系统在突发故障后能够可靠稳定地运行，由此设计出被动容错控制器；文献[4]针对航空工具发动机的主供油计量活门的执行机构突发故障等问题，先建立了数学模型，然后使用Lyapunov的稳定性定理，找出自适应的调节律，并以其最小化的输出误差做优化目标，设计出自适应容错控制器；文献[5]针对具有参数不确定和时延的NCS，当执行器突发故障时，对系统建立数学模型，利用Lyapunov稳定性定理、容错控制原理和LMI处理方法，设计出网络控制系统的H∞保成本容错控制器。本文针对含时延的NCS系统，当执行器突发乘性故障的情况下，对系统建立离散形式的数学模型，利用离散系统的有界实引理，设计了具有指数稳定的H∞容错控制器。

1问题描述

本文所研究的NCS系统结构如图1所示。

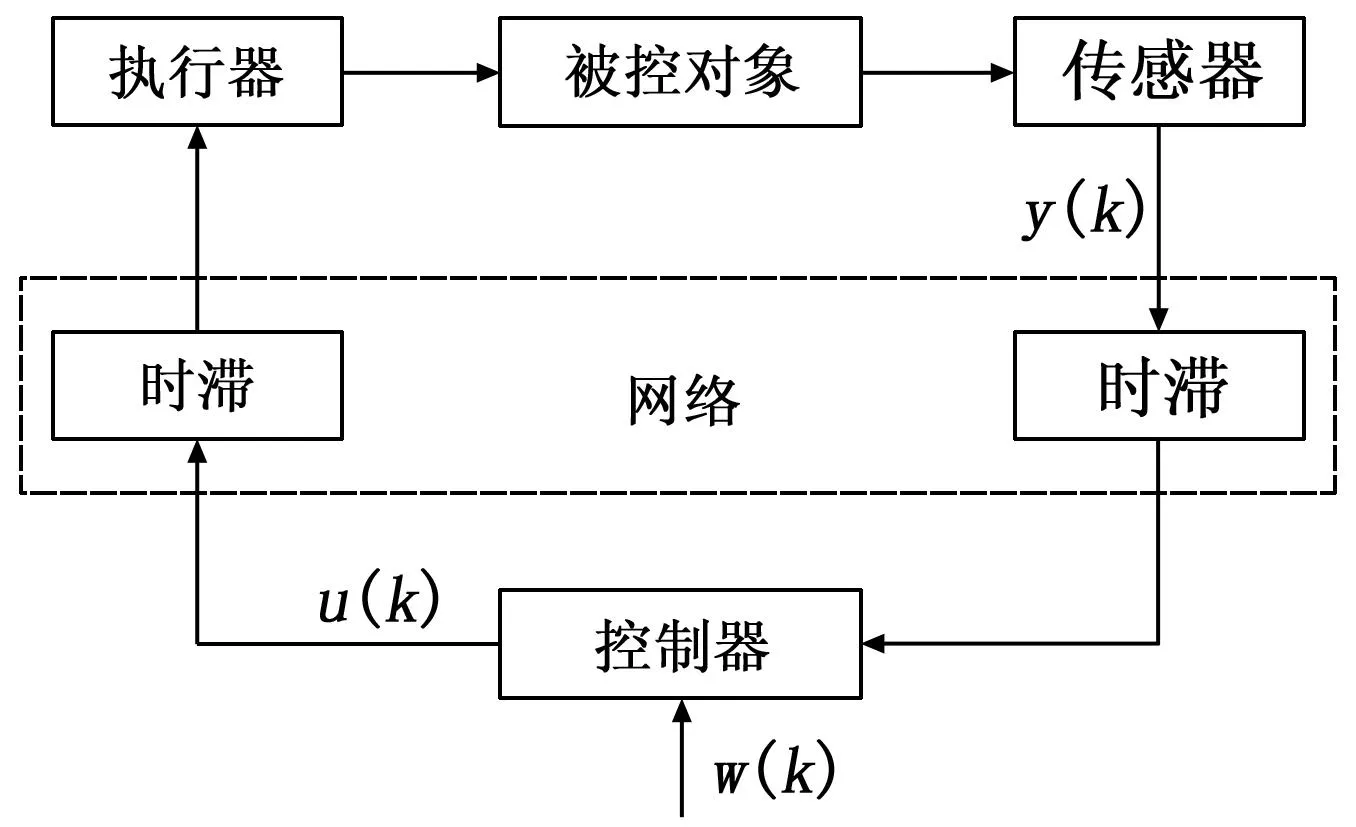
图1　NCS系统结构图

图1所示的NCS系统对应的离散模型如下所示：

(1)

其中：x(k)∈Rn为状态变量，u(k)∈Rm为输入变量，w(k)∈Rq为外部扰动输入，y(k)∈Rp为输出变量。系统矩阵A，Ad，B1，B2，C，Cd，D11，D12为相应维数的系数矩阵。

由图1我们可以看出,网络控制系统由多个传感器、执行器、控制器和被控对象构成，测量数据经由共享网络由传感器传输至控制器，控制器经过计算得到控制量，控制量再经由共享网络到达执行器，最后传输给被控对象。然而，系统因为网络的介入变得复杂。上述的特点导致在分析网路控制系统时必须考虑网络时延、节点驱动的方式、通信约束和数据包的丢失等问题。我们假设传感器和执行器采用时钟驱动，控制器采用事件驱动，且传输中数据无丢包和时序错乱现象。控制器采用事件驱动既可以避免控制器采用时钟驱动时等待被采样所浪费的时间，也避免了传感器和控制器时钟同步时面对的困难，还避免了无效采样、数据丢失等现象，减少了网络诱导时延并且提高了反馈数据的利用率。

很多系统在故障检测和诊断研究中出现的故障均用加性故障来表示，可是当控制系统的参数是变化时，乘性故障的表示方法更具有优越性[6]。本文考虑执行器突发故障是乘性故障时，则该系统的故障模型可表示如下：

(2)

其中：B,B2,D,D12为无故障时的系统矩阵，0≤Λ+Δ≤I，Λ=diag{λ1,λ2,...,λm}≥0是故障的模型，为已知实数矩阵；Δ=diag{δ1,δ2,...,δm}≥0是用以补偿真实的故障误差，为未知实数矩阵。λi和δi的取值表示控制发生的情况。

当故障发生时，故障诊断结果可以分为正常、效率下降和完全失效3种状态，则对于第k个执行器，可分别表示为如下形式

(3)

设所有执行器故障模式的集合为I，其中的第i个故障模式可以表示为i∈I或Λi∈I。如果故障模式Λi和Λj同时存在，且满足Λi-Λj≥0，则Λi≥Λj。从而定义集合P(Λi)={Λj|Λj≥Λi}和集合S(Λi)={Λj|Λi≥Λj}[7]。下面针对系统(1)中的执行器突发故障时，设计容错控制器。

2H∞指数稳定容错控制器设计

对于系统(1)，当执行器突发故障时，设计以下的状态反馈控制器：

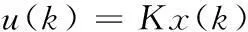
(4)

使得系统

是指数稳定的，且该系统对应的闭环传递函数[G(k)](z)满足

则式(4)是系统(1)的H∞指数稳定容错控制器。

引理1[8]：系统为内部正系统，其中传递函数

G1(z)=(C+Cdz-d)[zI-(A+Adz-d)]-1B+D。则下列叙述等价：

1)‖G1(z)‖∞<1且系统指数稳定；

2)存在正定对称矩阵P>0，Q>0满足

(5)

式中,*表示矩阵的对称部分,其中

引理2[9]: 无外部扰动输入的内部正系统指数稳定当且仅当存在对角矩阵D>0，矩阵Q>0满足

其中:A和Ad为正矩阵。

1) S<0；

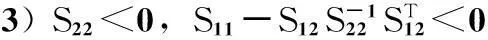
定理1: 针对系统(1)，假设(A,C)为可检测，当执行器突发故障为(2)式所示的乘性故障Λi时，如果存在正定对称矩阵P和Q，任意矩阵Z，使得矩阵不等式(6)成立，则u(k)=Kx(k)为系统的H∞容错控制器，并且反馈矩阵K=ZP

(6)

其中:Xi=P-1，S=P-1QP-1

证明：

针对系统(1)，根据引理3可得

(7)

其中：

对式(7)利用Schur补引理，等价于

(8)

对式(8)两侧均乘以矩阵diag{P-1,P-1,I,I,P-1}得式(9):

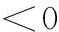
(9)

令 S=P-1QP-1，Xi= Pi- 1则式(9)等价于不等式(6)。令K=ZP,则控制器u(k)=Kix(k)是Λi的一个可行控制器。

定理2:假设系统(1)，(A，C)为可检测，当执行器突发两个故障模式Λi,Λj时，其中Λi,Λj∈I+，且Λi≥Λj，如果存在任意矩阵Z和正定对称矩阵P、Q，使得矩阵不等式(10)成立，那么控制器u(k)=Kjx(k)的一个可行的容错控制器为:

(10)

证明：将Λj代入公式(5)利用Schur补引理，变换为:

(11)

对式(11)两侧均乘以矩阵diag{P-1,P-1,I,I,P-1}，得到下式:

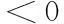
(12)

得证。

3数值仿真

针对系统(1)，设置其参数矩阵为：

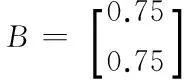
D=0.0625

D11=0.25

通过LMI工具箱进行计算，得到的可行解为:

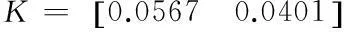
首先初始化网络控制系统中的节点，并将以上求得的结果带入到仿真图中设置相应的任务，接下来对网络控制系统实施干扰，使执行器出现故障，通过Matlab进行仿真，并得到相应的状态相应曲线如图2~3所示。

图2　状态x1 的响应曲线

从以上两图的状态曲线可知，虚线为执行器无故障时的曲线，而实线为执行器出现故障的仿真曲线。利用离散系统的有界实引理，对于系统(1)中由于网络导致的时延拥有良好的控制效果，并且当系统在执行器出现乘性故障时具有很好的容错控制功能，可以使系统达到渐进稳定。

4结论

本文通过对具有时延的NCS，首先分析了执行器出现乘性故障时的情况，然后给定乘性故障的模型，结合离散化的网络控制系统模型，先后分析了一个故障模式和两个故障模式出

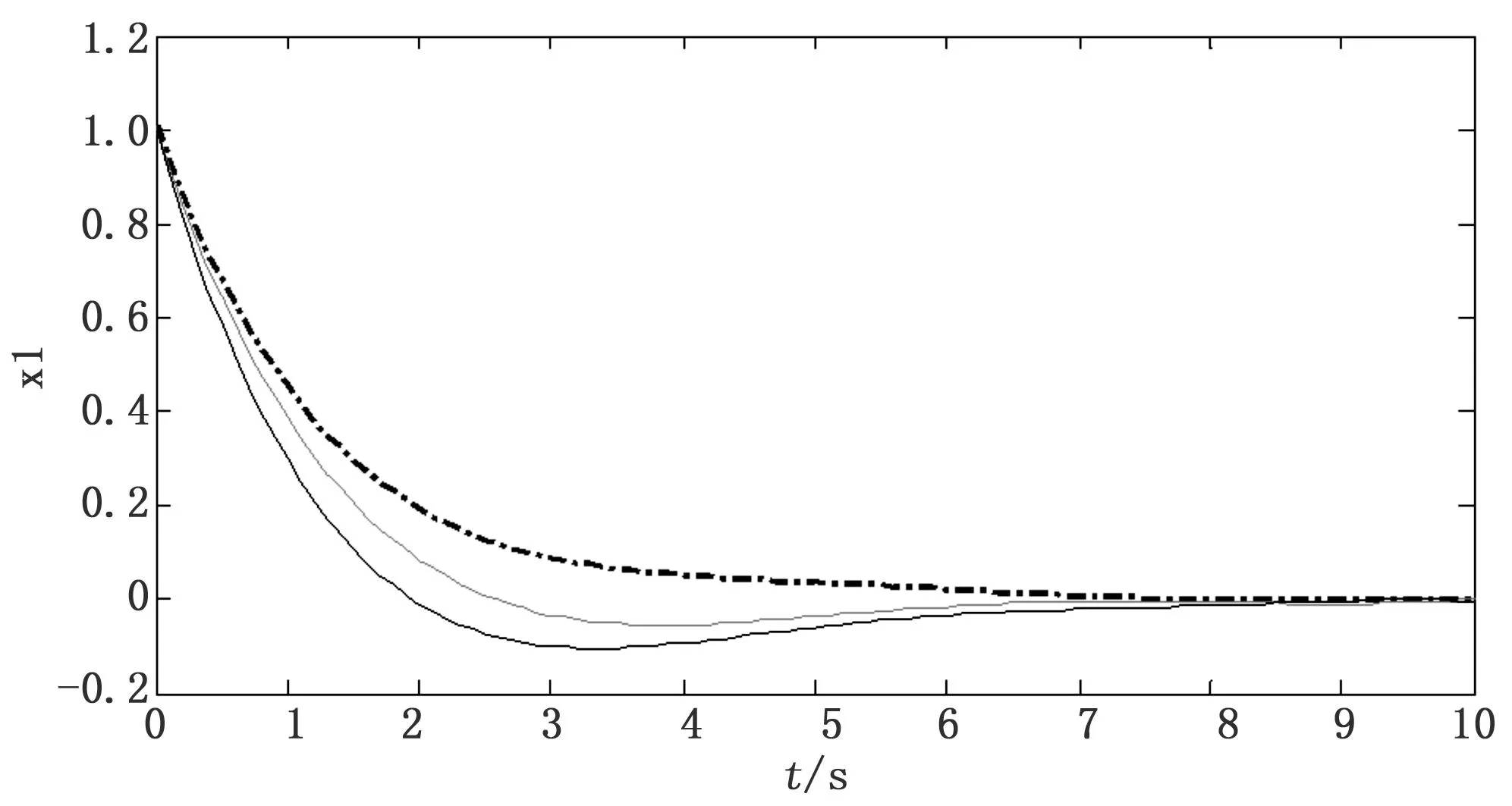
图3　状态x2 的响应曲线

现的情况，并针对该系统设计了H∞指数稳定容错控制器，最后通过LMI工具箱证明了设计的容错控制器对执行器出现的故障具有很好的控制作用，很有效。

参考文献：

[1]卢军锋,吴钟鸣,王荣浩.不确定非线性切换系统鲁棒容错H∞控制与仿真[J].计算机仿真,2013,30(6):320-325.

[2]沈艳霞,贺庆楠,潘庭龙,等.风能转换系统T-S模糊鲁棒容错控制[J].信息与控制,2013,42(6):750-757.

[3]傅强,樊丁.航空发动机被动容错控制器优化设计研究[J].热能动力工程,2013,28(1):28-32.

[4]傅强,樊丁,彭凯.航空发动机主供油计量活门故障主动容错控制器设计[J].航空动力学报,2014,29(4):973-979.

[5]刘新娟,孙文安,李丕贤,等.一类时延网络控制系统的H∞容错保成本控制[J].计算机工程与应用,2013,49(24):224-228.

[6]赵瑾,顾幸生.动态不确定系统的鲁棒乘性故障检测与重构[J].中南大学学报:自然科学版,2007,32(7):810-813.

[7]于臻,刘利军,沈毅.H∞容错控制器设计设计及在线优化选择容错控制[J].控制理论与应用,2014,31(4):417-424.

[8]杨慧丽.时滞正系统的有界实引理及H∞状态反馈控制器设计[D].山西：山西师范大学，2013:31-37.

[9]Wu L, Lam J, Shu Z,et al. On stability and stability of positive delay systems[J]. Asian Journal of Control, 2009,11(2):226-234.

[10]俞立. 鲁棒控制——线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.

[11]陈青,吴敏.具有网络丢包和时延的网络控制系统设计[J].控制与决策,2011,26(2)：293-296.

Design of H∞Fault-tolerant Controller for Networked Control System

Zhang Peng,Gong Zhanxia

(School of Automation, Harbin University of Science and Technology, Harbin150080, China)

Abstract:With the wide application of the network control system, the fault-tolerant control problem has also become the focus of research . In spite of many fault-tolerant control methods have been proposed, there are still some conditions were ignored . Proposing a design in order to achieve better control of fault-tolerant : for a class of networked control systems with time delay, when the actuator failed because of the multiplicative fault,we discrete the mathematical model of the system,using the bounded real lemma of the discrete system, and designing a H∞fault-tolerant controller of exponentially stable .Then working out the state feedback matrix by using LMI toolbox, get the fault-tolerant controller . The data sample proves the controller can meet the requirements of the design, and can achieve good fault-tolerant control.

Keywords:networked control systems; multiplicative fault; fault-tolerant controller; exponentially stable

文章编号：1671-4598(2016)02-0088-03

DOI：10.16526/j.cnki.11-4762/tp.2016.02.024

中图分类号：TP273

文献标识码：A

作者简介：张鹏(1977-)，男，黑龙江哈尔滨人，副教授，硕士研究生导师，主要从事控制系统的鲁棒控制，网络控制系统等方面的教学和科研工作。宫占霞(1989-)，女，黑龙江哈尔滨人，硕士研究生，主要从事控制理论与控制工程，网络控制系统方向的研究。

收稿日期：2015-12-03；修回日期：2015-12-31。