起落架磁流变减摆器模糊PID控制算法的研究
2016-03-17祝世兴
李 莹,王 博,祝世兴
(中国民航大学 航空工程学院,天津 300300)
起落架磁流变减摆器模糊PID控制算法的研究
李莹,王博,祝世兴
(中国民航大学 航空工程学院,天津300300)
摘要:为了减小飞机机轮的摆振,提高飞机乘坐的舒适性和驾驶的安全性,将磁流变控制技术应用于飞机起落架减摆器,实现减摆器阻尼力的实时智能控制;针对磁流变减摆器,建立了飞机起落架摆振的半主动控制非线性动力学模型,设计了模糊PID控制算法,并使用Matlab/Simulink建立了半主动控制仿真模型;通过调节流过磁感线圈的电流大小改变磁流变减摆器的阻尼力,从而减小机轮摆动实现半主动控制;通过动力学仿真,在给定速度下分别对比未安装减摆器、被动控制下以及半主动控制下机轮摆角、侧向位移、侧滑角随时间变化的曲线,结果表明了模糊PID控制算法的正确性和可行性,该控制策略可以较好的抑制机轮的摆振,同时也表明模糊PID控制算法具有良好的可控性,减摆效果也明显优于传统的被动控制。
关键词:非线性摆振模型;磁流变减摆器;半主动控制;模糊PID
0引言
飞机在起飞或者着陆滑跑时前轮有时会发生一种偏离其中心位置的侧向摆动,这种摆动主要是前轮摆动部分绕其定轴交变地转动,同时轮胎和地面接触的部分相应地发生交变的变形[1]。飞机前轮摆振是飞机研制和使用过程中一种常见的现象,若不加以控制会对飞机安全造成严重威胁,因此减小或者避免起落架前轮的摆振显得极为重要。迄今为止,防止前轮摆振的最有效的方法是加装减摆器,其核心是阻尼力的调节。为了防止前轮摆振现代飞机广泛采用油液减摆器。传统油液减摆器的阻尼力不能根据外载荷的变化实时控制,因此其减摆效果和控制策略尚有许多提高和改进之处。近年来,随着人们对半主动控制技术的不断研究,研制了多种类型的智能流体减摆器,其中磁流变减摆器就是其中一种。磁流变减摆器随外加磁场的变化其阻尼力发生变化,具有良好的可控性,因而已逐渐成为阻尼器研究的热点[4]。本文结合现有研究成果,建立了起落架前轮摆振半主动控制的动力学模型,并针对现有的磁流变减摆器设计了模糊PID控制算法,模糊PID控制是将模糊控制与PID控制相结合,具有结构简单,参数灵活,可靠性高,鲁棒性强等诸多优点,通过仿真证明,该模糊PID控制对于磁流变减摆器来说是一种较为理想的控制策略[9-14]。
1起落架摆振半主动控制动力学模型
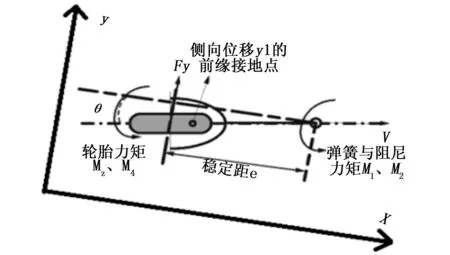
图1 摆振动力学模型示意图
飞机在地面滑跑到一定速度时,如果由于跑道不平、侧风和操纵不当等外力干扰,使前轮偏离前进轴线一段距离y1,由于机轮的弹性和回复力的作用,使机轮继续前进时,机轮偏转了一个角度θ;同时,产生了一个与前进轴线方向靠近的趋势,当恢复到前进轴线时,由于惯性作用,又使前轮偏离前进轴线一段距离y1,如此反复前进,飞机前轮就可能绕着飞机前进轴线不停地左右摆动,使飞机前轮的轮迹呈一条S形曲线。这种左右摇摆的振动,称为前轮摆振[6]。图1所示为非线性的摆振数学模型,根据起落架运动学和动力学,首先建立具有磁流变减摆器的非线性摆振半主动控制的数学模型,该模型方程包括起落架支柱扭转动力学方程和轮胎侧向运动方程[3,8],其中轮胎模型按照张线理论给出[7]。具体方程如下:
(1)
其中:M1(θ)=Kθ M2(θ)=Cθ,M3(θ)=Mz-eFy,
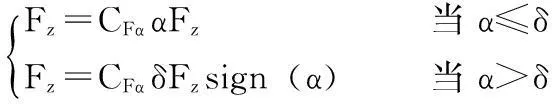

式中,Iz为Z轴的惯性矩;M1为支柱扭转刚度引起的力矩;M2为由支柱的扭转阻尼引起的力矩;M3由轮胎中心的回正力矩Mz和以稳定矩为力臂的侧向力Fy组合而成;M4为阻尼力矩,取决于速度、轮胎胎面宽度及扭转角速度;M5为磁流变减摆器的减摆力矩;C为支柱的扭转刚度;K为扭转阻尼系数;Cma为轮胎回正力矩系数;CFa为轮胎侧向力系数;δ为轮胎侧向力引起的极限侧滑角;αg为回正力矩引起的极限侧滑角;Fz为垂直载荷;κ为轮胎胎面宽度力矩常数。y1为轮胎接触点的侧向位移;V为机轮向前速度; θ为起落架支柱的扭转角;e为机轮的稳定矩;h为轮胎与地面接触长度;σ为轮胎的松弛长度。
侧滑角和侧向位移的关系如下:
轮胎胎面宽度力矩常数与触地半长,侧向力系数与垂直载荷的关系如下:
κ=-0.15a2CFαFZ
磁流变减摆器的减摆力矩为:
M5=f(t)d
按照Bingham平板模型[9],剪切阀式磁流变减摆器的阻尼力可以表示为:
其中:f(t)为磁流变阻尼器减摆阻尼力,d为减摆力臂,C为粘滞阻尼系数,其大小不受磁场强度大小影响,u为磁流变装置的相对运动速度,在非线性的摆振数学模型中,其大小与起落架支柱的扭转角有关系,fc为与磁场强度相关的可控阻尼项,因而改变磁场强度大小即可以改变磁流变阻尼器减摆阻尼力,即改变控制电流的大小即可改变磁流变阻尼器减摆阻尼力。
磁流变液剪切应力与电流大小的关系的实验数据如图2所示,图示为两次实验数据,取电流大小为0~2A的一段为研究对象,通过拟合可以得出剪切应力τy(纵坐标)与电流大小I(横坐标)的关系如下:
τy=231.58I2+833.4I
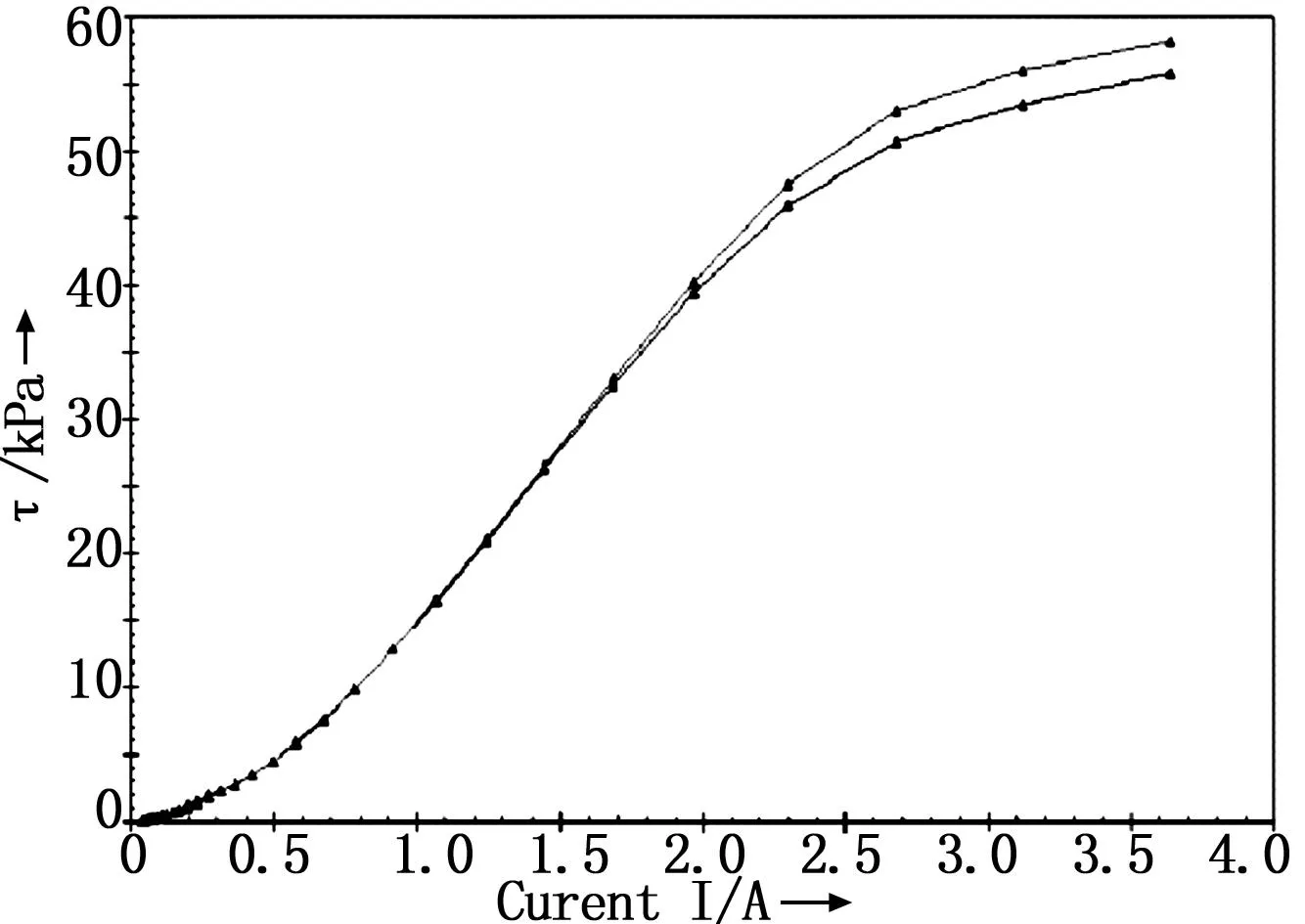
图2 电流与剪切应力关系
2模糊PID控制器设计
2.1控制策略
采用自适应模糊PID控制策略进行控制,取误差及其误差变化率作为控制器的输入,选定减摆器振动位移与给定值的差为误差e,误差变化率为振动位移与给定值的差的变化率ec,输出量为可变电流值,在运行的过程中不断检测误差及其误差的变化率,利用模糊规则在线对PID的参数进行修改,以满足不同误差及其误差变化率对控制器参数的不同要求。通过模糊PID控制器调节PWM信号,得到磁流变减摆器的控制电流,从而达到精确地、实时地调节磁流变减摆器阻尼力的目的,使被控对象具有良好的可控性。

图3 模糊PID控制原理
2.2确定模糊控制器的输入输出量
建立模糊PID控制器之前,需确定模糊控制器的输入误差e、误差变化率ec及输出K′p,K′i,K′d。输入变量e,ec采用7个词汇来描述,即{负大、负中、负小、零、正小、正中、正大},其论域为[-3,3],所对应模糊子集为{NB、NM、NB、ZO、PS、PM、PB}。输出变量Kp’,Ki’,Kd’采用7个词汇来描述,即{负大、负中、负小、零、正小、正中、正大},其论域为[-1,1],所对应模糊子集为{NB、NM、NB、ZO、PS、PM、PB}。输入的隶属度函数采用高斯隶属函数,输出的隶属度函数采用三角形隶属函数。推理方法采用三角Mamdani方法。
2.3设计模糊控制规则
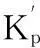
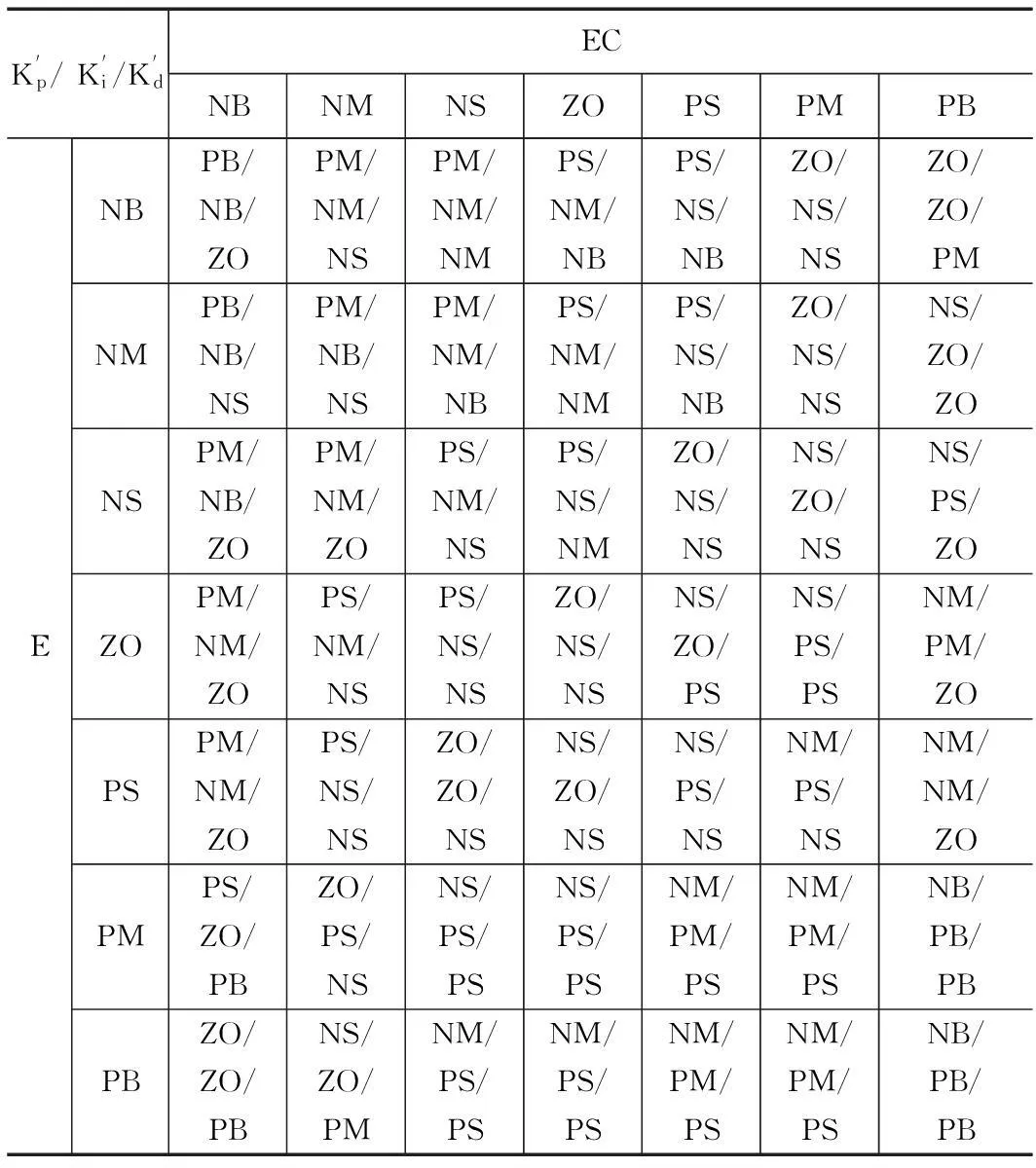
表1 模糊控制规则表
2.4模糊曲面图
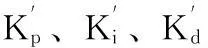

图模糊曲面
3仿真与结果分析
3.1Matlab/Simulink建模仿真
根据式(1),利用Matlab/Simulink建立摆振半主动控制模型,建立好的模型如图5所示,系统模型参数、减摆器参数如表2,表3所示。
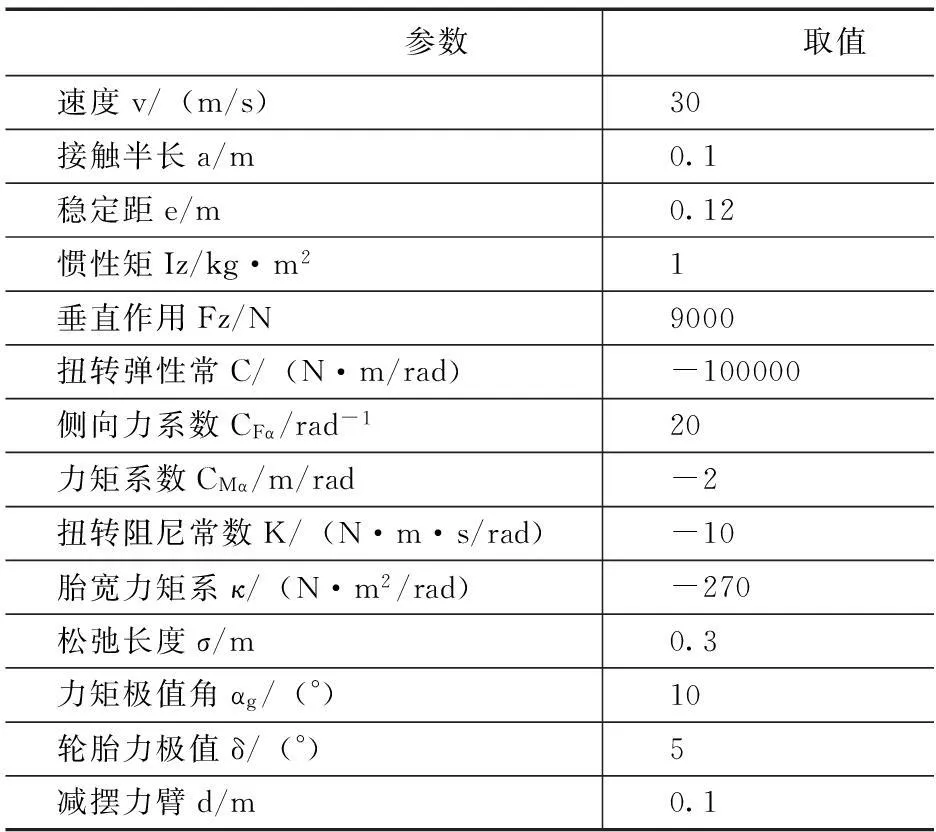
表2 系统模型参数
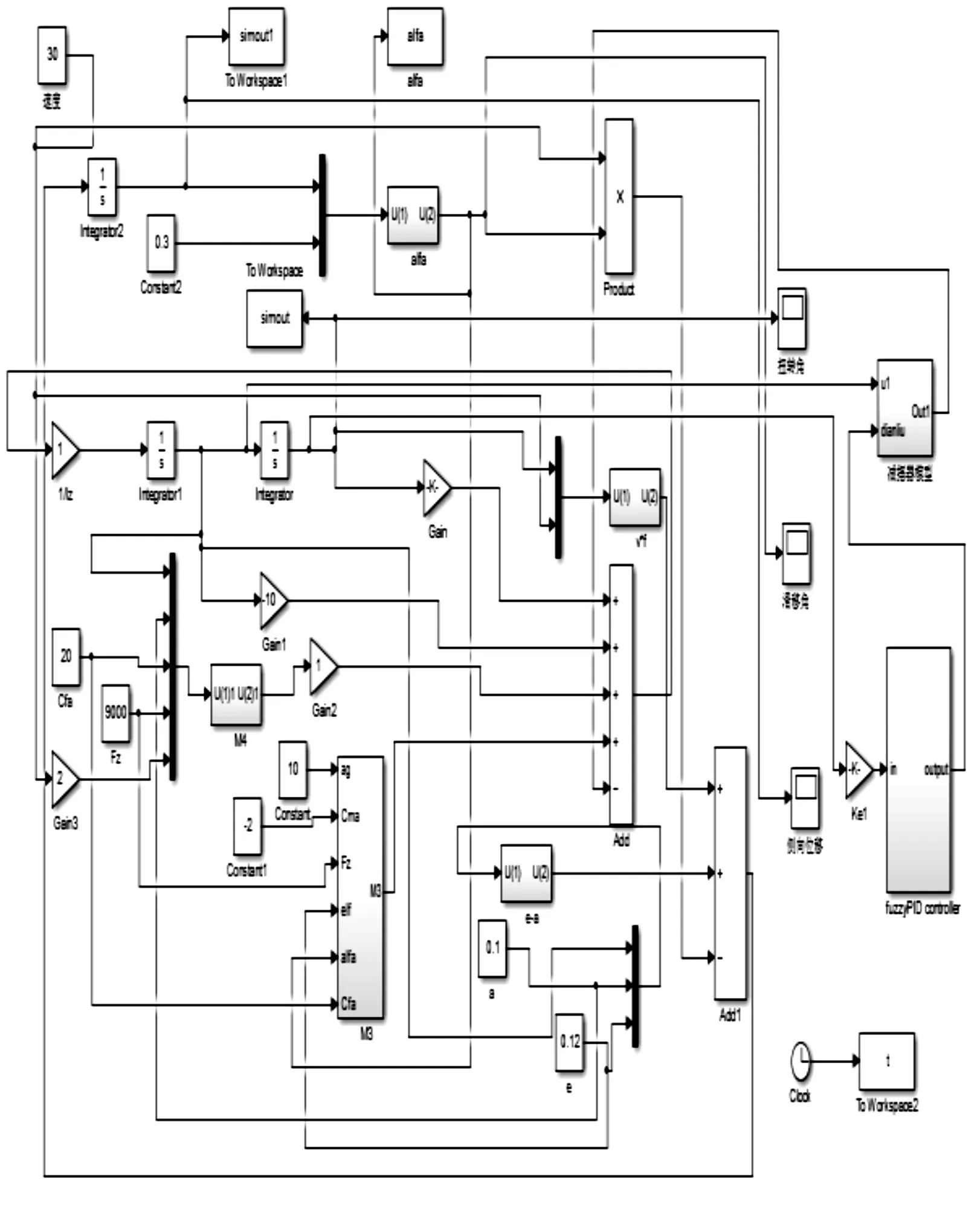
图5 模型仿真
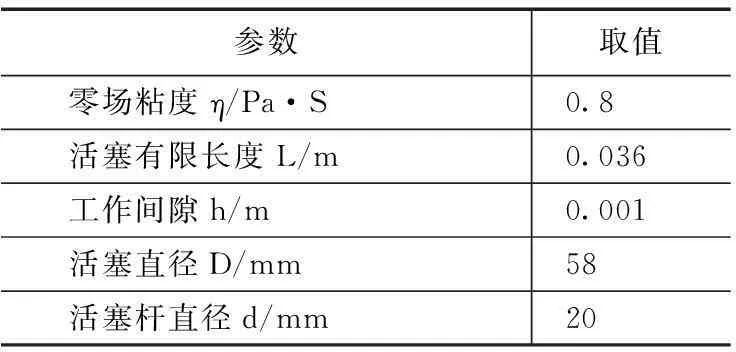
参数取值零场粘度η/Pa·S0.8活塞有限长度L/m0.036工作间隙h/m0.001活塞直径D/mm58活塞杆直径d/mm20
3.2仿真结果分析
1)未加装磁流变减摆器时仿真:在速度为V=30 m/s,扭转阻尼常数K=-10,机轮初始状态的机轮摆角为0.01,轮胎触地侧向位移为0时,未加装磁流变减摆器(即式(1)中M5=0)时,机轮摆角,轮胎触地侧向位移,滑移角随时间的变化如图6所示,其中机轮摆角θ、侧向位移y1、侧滑角α的值一开始随时间不断增大,达到稳定幅值后保持等幅振动,由此看出,此时机轮发生了稳定的摆振。
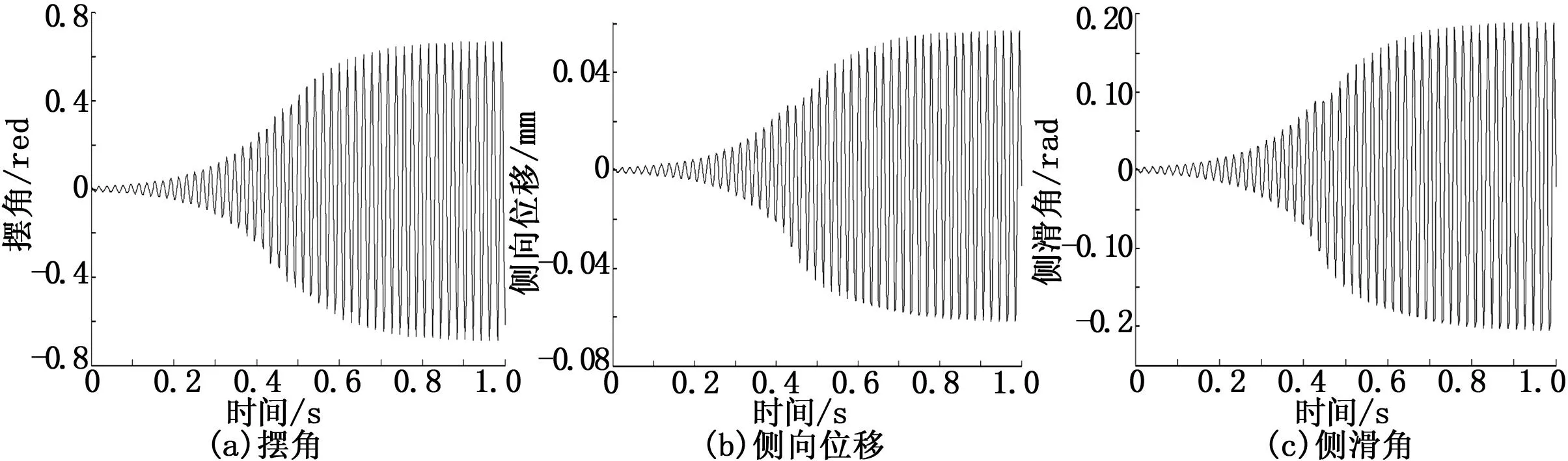
图6 未加装减摆器时性能仿真曲线图
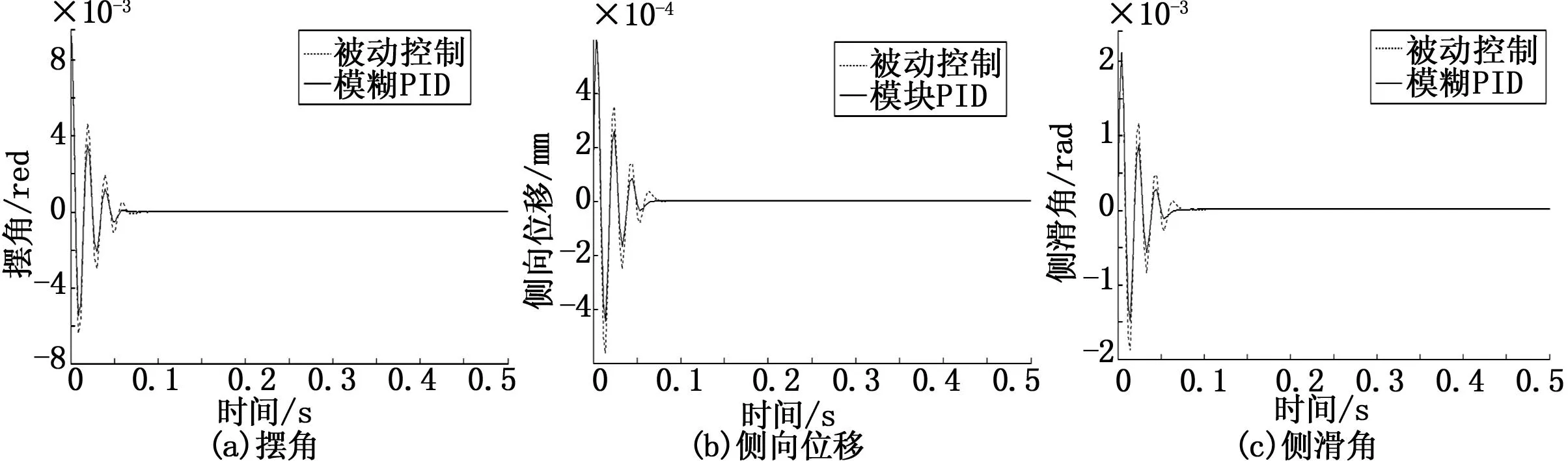
图7 被动控制与模糊PID控制性能仿真曲线图
2)被动控制与半主动控制比较:在速度为V=30 m/s,扭转阻尼常数K=-10,机轮初始状态的机轮摆角为0.01,轮胎触地侧向位移为0时,安装磁流变减摆器后,被动控制及加入模糊PID控制器之后,机轮摆角,轮胎触地侧向位移,滑移角随时间的变化如图7所示。
分析被动控制与半主动控制时机轮摆角θ、侧向位移y1、侧滑角α的峰值,通过计算峰值差值的百分比,来评价模糊PID控制对振动峰值衰减能力的控制效果,结果分析如表4所示。
3)结果与分析:本文在总结现有文献的基础上,建立了飞机起落架摆振的半主动控制非线性动力学模型,并设计了磁流变减摆器的控制方法,通过仿真实验可以得出:模糊PID具有良好的控制效果,在给定速度、扭转阻尼常数和其他初始状态下,未使用减摆器时机轮发生了稳定的摆振,在加入磁流变减摆器后,原本发生的摆振幅度逐渐减小并在短时间内迅速趋于稳定,加入模糊PID控制策略后,机轮摆角、侧向位移、侧滑角随时间变化的幅值均有所减小,并且趋于稳定所需的时间更短一些,可以证明,相比传统的被动控制,此次设计的控制算法具有较好的控制效果,这也验证了模糊PID方法应用于磁流变减摆器的可行性。

表4 效果分析
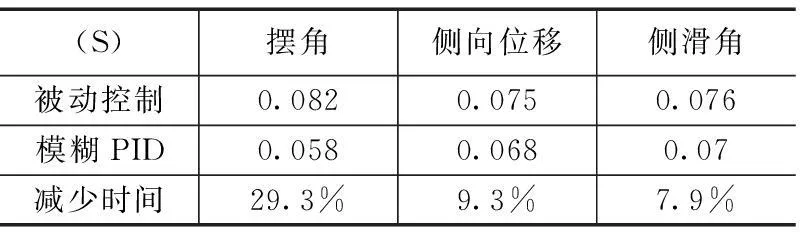
表5 趋于稳定所用时间分析
参考文献:
[1] 诸德培.摆振理论及防摆措施[M].北京:国防工业出版社,1983.
[2] 周云,谭平.磁流变阻尼控制理论与技术[M].北京.科学出版社.2007.
[3] Gerhard Somieski.Shimmy analysis of a simple aircraft nose landing[J].Aerospace, 1997, 8(1):545-555.
[4] Zong L H, Gong X L,Guo C Y, et al.Inverse neuro-fuzzy MR damper model and its application in vibration control of vehicle suspension system[J].Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility, 2012, 50(7):1025-1041.
[5] Mario Lafontaine, Ofelia Moroni, Mauricio Sarrazin,et al.Optimal Control of Accelerations in a Base-Isolated Building using Magneto-Rheological[J].Journal of Earthquake Engineering, 2009, 13(8):1153-1171.
[6] 聂宏,魏小辉.飞机起落架动力学设计与分析[M].陕西:西北工业大学出版社,2012.
[7] 陈大伟.起落架摆振的非线性分析及控制[D].南京:南京航空航天大学,2011.
[8] 骆存琪.机轮摆振及轮胎动力学分析研究[D].南京:南京航空航天大学,2007.
[9]李忠献,徐龙河.新型磁流变阻尼器及半主动控制设计理论[M].北京:科学出版社,2012.
[10]杨亚珣.基于智能PID控制的车辆磁流变阻尼器座椅悬架研究[D].哈尔滨:东北林业大学,2009.
[11]贾红玉,武晓娟.基于磁流变缓冲器的飞机起落架模糊控制[J].北京航空航天大学学报,2008,33(11):1264-1267.
[12]田静,何军,祝世兴.基于磁流变减震器的飞机起落架模糊控制研究[M].机床与液压,2010(7).
[13]吴九山. 车辆半主动悬架模糊PID控制仿真及试验研究[D].南京:南京林业大学,2008.
Study on Magnetorheological Shimmy Damper Control Algorithm using Fuzzy PID
Li Ying,Wang Bo, Zhu Shixing
(Institute of Aeronautical Engineering, Civil Aviation University of China, Tianjin300300, China)
Abstract:In order to reduce the aircraft wheel shimmy,enhance the comfort and safety of the aircraft,apply the magnetorheological (MR) control theory into shimmy damper of aircraft landing gear,achieve the real time and intelligent control.According to magnetorheological (MR) shimmy damper, the semi-active control of a nonlinear dynamic model of the landing gear was established.FuzzyPID control algorithm was set up. And the model of semi-active control was created by using Matlab/Simulink.It adjusted the damping force of magnetorheological(MR) shimmy damper by controlling the current which flows through the magnetic coil. Therefore, it can reduce the swing of the wheels. The semi-active control for magnetorheological(MR) shimmy damper was realized. By using dynamic simulation, comparing non-magnetorheological(MR) shimmy damper, passive control and semi-active control, we get the time curves of oscillation angle, the lateral displacement and the angle of the side slip. The simulation results show that FuzzyPID control algorithm was correct and feasible,the algorithm can good restrain the shimmy of airplane wheel,The results also show that FuzzyPID control algorithm has good controllability, the effect of diminishing oscillation is also better than the traditional passive control.
Keywords:nonlinear oscillating model; magnetorheological(MR) shimmy damper; semi-active control; fuzzy-PID
文章编号:1671-4598(2016)02-0080-04
DOI:10.16526/j.cnki.11-4762/tp.2016.02.022
中图分类号:V226.4
文献标识码:A
作者简介:李莹(1991-),女,河南人,硕士研究生,主要从事飞机起落架震动控制、飞机维修理论与技术方向的研究。祝世兴(1958-),男,黑龙江青冈人,教授,主要从事飞机起落架震动控制、飞机维修理论与技术方向的研究。
基金项目:国家自然科学基金项目(61172013)。
收稿日期:2015-08-13;修回日期:2015-09-17。
