一类拟线性椭圆型方程div(|Du|p-2Du)=f(x,u,Du)的有界正整解1
2016-03-16许兴业
许兴业
(广东外语外贸大学南国商学院公共课教学部;广东广州 510545)
一类拟线性椭圆型方程div(|Du|p-2Du)=f(x,u,Du)的有界正整解1
许兴业
(广东外语外贸大学南国商学院公共课教学部;广东广州 510545)
以Schauder-Tychonoff不动点定理为工具;研究一类形如div(|Du|p-2Du)=f(x,u,Du)的拟线性椭圆型方程正的有界整体问题;得到了2个有界正整解的存在性定理.
拟线性椭圆型方程;有界正整解;Lebesgue控制收敛定理;闭凸子集;连续映照;不动点定理
1 引言与预备定理
有关非线性椭圆型方程正整解存在性的研究;较多的文章是研究方程左边为形如Δu,Δ2u及Δmu的调和;双调和及多重调和方程[1-5].但对形如下面的拟线性椭圆型方程
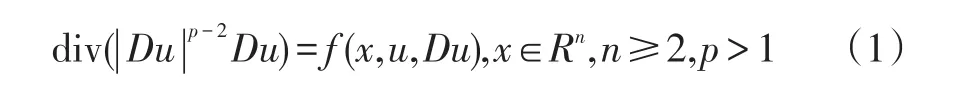
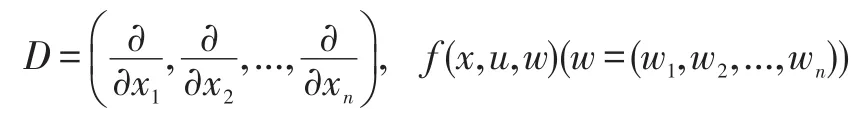
下面给出上、下解的定义及预备定理.

预备定理设f满足条件:
(a)f(x,u,,w)在Rn×R+×Rn上连续;且局部Holder连续(指数θ∈(0,1));(b)对任一有界区域Ω⊂Rn,存在ρ(Ω,M)> 0;使
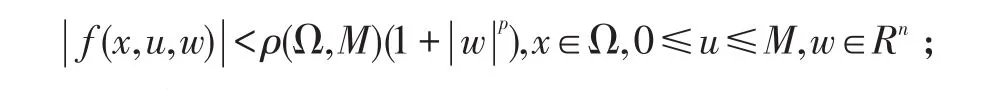

预备定理的证明参见文献[1].
2 主要结果
在下面的讨论中引入记号;不再赘述:

定理1设f满足预备定理中的(a)、(b)、(c)和下列条件:
(i)f1(r,u,v)与f2(r,u,v)关于u,v∈R+都是非减函数;
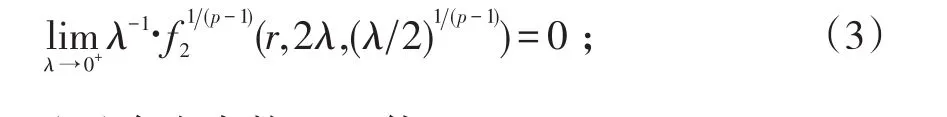
(iii)存在常数c>0使

则方程(1)存在无穷多个有界正整解u(x).
证明由(2)式可知方程
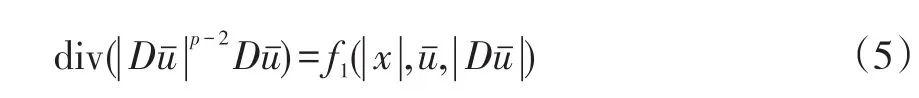
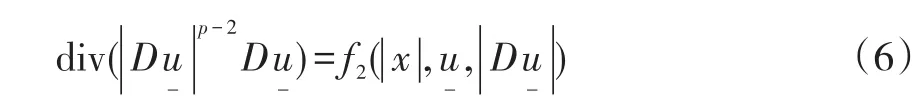

下面讨论积分方程(8)的可解性.由(ii)知

其中c是(iii)中出现的常数;且对每一s∈(0,∞),当λ→0+时有
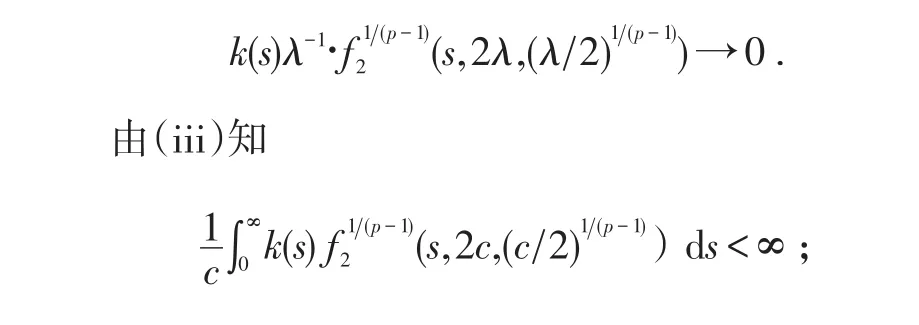
于是由Lebesgue控制收敛定理得

进而由(2)推出:对∀p>1有
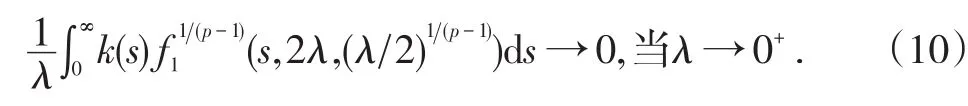

由(10)知可以选择充分小的常数η>0使得记C1[0,∞)是定义在[0,∞)上的所有连续可微函数作成的空间;依通常的方法引入C1[0,∞)的拓扑.作集合:

在这里补充定义:
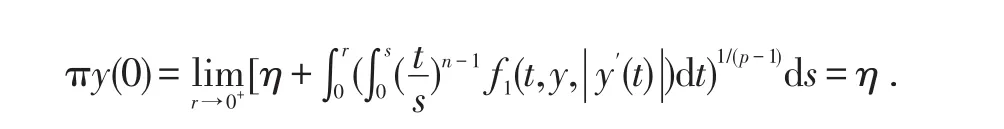
下面证明映射π满足:

(II)π是连续映射.
设yi∈Σ(i=1,2,...)且依C1[0,∞)的拓扑yi收敛于y;对∀r∈[0,∞)由(12)、(14)式得
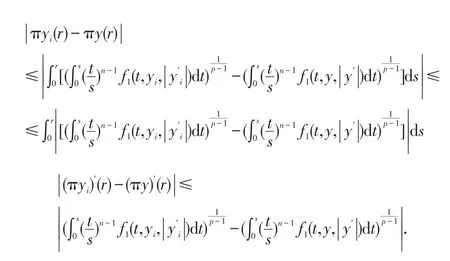
(III)πΣ是相对紧的.

又注意到(12)式中的r≥ 0;及f(r,u,v)≥0

对(17)式右边的积分我们约定

于是(17)式对任意r≥0成立.故有

由上式看到{(π′)|y∈Σ}在[0,R]上等度连续.故对[0,∞)的任一紧子区间[0,R];依C1[0,∞)的拓扑能用Ascoli-Arzela定理[7].
要证明πΣ在Σ中是相对紧的;即要证πΣ中任一序列{(πyi)(r)}必包含一个子序列;该子序列依C1[0,∞)的拓扑收敛于Σ中的一个元素;只需对区间列[0,R1]⊂[0,R2]⊂…⊂[0,Rj]⊂…,(其中Rj→∞,当j→∞时)逐次利用Ascoli-Arzela定理;并采用“取对角线子列”手续即可完成.
以上证明了Schauder-Tychonoff不动点定理[8]的条件全部满足;所以π存在不动点y∈Σ.
同前面类似;对方程(6)作相应的初值问题:
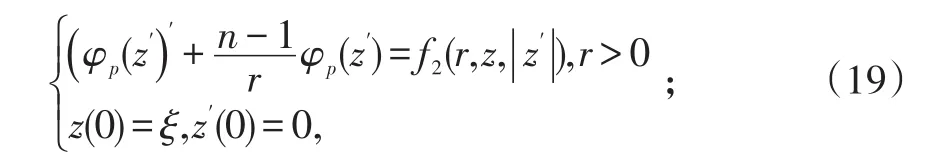
其中ξ是待定常数;进而作与(19)等价的积分方程:
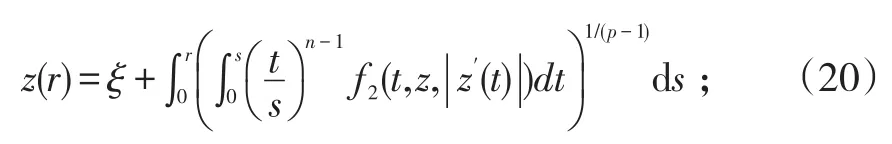
由(11)知可选充分小的常数ξ> 0;满足

类似前面可得πˉ存在不动点z∈Γ.
如果上面待定常数η与ξ除了满足(11)与(21)外还满足2ξ≤η(选择ξ满足(21);固定ξ;然后选取η使它满足2ξ≤η及(11));于是有
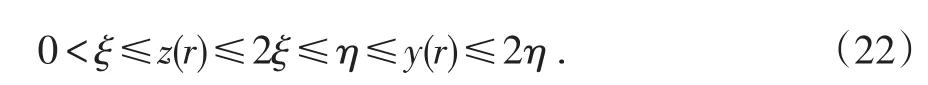
在证明定理开始一段已经解释过如果积分方程(8)有解y(r);则v(x)=y|x|=y(r)便是初值问题(7)的解;也是方程(1)的上解.类似如积分方程(20)有解z(r);则w(x)=z|x|=z(r)便是初值问题(19)的解;也是方程(1)的下解.由(22)得
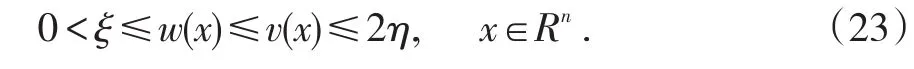
由预备定理知存在方程(1)的解u(x)满足

以上证明了方程(1)存在正的有界径向对称整体解u(x).从(23)和(24)看出所得到的正整解u(x)的上、下界取决于充分小的正数ξ,η的选择;如果我们选取合适的数对(ξj,ηj)(j=1,2,3,…);使用闭区间集{[ξj,ηj]|j=1,2,…}中的闭区间互不相交;那么我们得到方程(1)无穷多个互异的有界正整解uj(x),(j=1,2,3,…).(定理证毕)
定理1′设f满足预备定理中的假设(a);(b);(c)和定理1中的条件(i);(iii)及下面条件:

则方程(1)存在无穷多个有界正整解u(x).
证明由于定理(1)′与定理1的差别只是第二个条件;故只需把定理1证明过程中“可以选择充分小的常数η>0使得”即可;其余完全与定理1的证明类似.
定理2设f满足(a)、(b)、(c)和下列条件:
(i)f1(r,u,v)与f2(r,u,v)关于u,v∈R+都是非增函数;
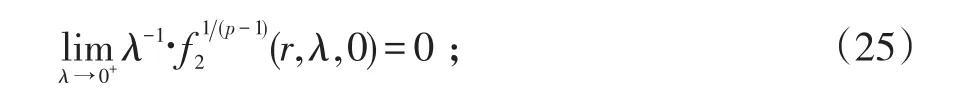
(ii)′λ-1∙f1(p-1)2(r,λ,0)关于λ∈(0,∞)是非增函数;且对每一固定的r∈R+;有

(iii)存在常数c>0使
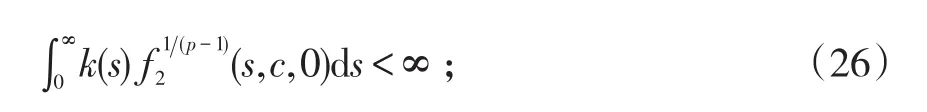
则方程(1)存在无穷多个有界正整解u(x).
证明定理2的证明过程与定理1的证明过程完全类似.略.
[1]NOUSSAIR E S,SWANSON C A.Postive Solutions of Quasilinear Elliptic Equations in Exterior Domains[J].J.Math.Anal.Appl.1980(75):121-133.
[2]KAWANO N,KUSANO T,NAITO.On Tne Elliptic EquationsΔu=Φ(x)uγinR2[J].Proc Amer Math Soc;1985(93):73-78.
[3]GUEDDA M,VERON L.Local and Global Properties of Solutions of Quasilinear Elliptic Equations[J].J.Differential Equations. 1988(76):159-189.
[4]许兴业.一类非线性椭圆型方程的正整解[J].数学杂志;1996,16(4):403-411.
[5]XINGYE X,LUANYING L,DEBNATH L.Existence of Positives Solutions of Singular Elliptic Boundary Value Problems In A Ball[J].Computers and Mathematics with Applications[J].2011(61):1335-1341.
[6]许兴业.可化为常微分方程的一些偏微分方程[J].广东教育学院学报,1999(5):39-44.
[7]ADMAS R A.Sobolev Spaces[M].Boston:Acamdemic Press,1975.
[8]EDWARDS R E.Functional Analysis[M].New York:Rinchart and Winston,1995.
【责任编辑:吴跃新】
Quasilinear Elliptic Equations Such asdiv(|Du|p-2Du)=f(x,u,Du)
XU Xing-ye
(Department of Public Course Teaching,South China Business College,Guangdong University of Foreign Studies,Guangzhou 510545,Guangdong China)
In this paper we study the problem of bounded positive entire solutions of a class of the quasilinear elliptic equations such as with the Schauder-Tychonoff fixed point theorem as the principal tool and have attained two theorems of existence bounded positive entire solutions.
quasilinear elliptic equations;bounded positive entire solutions;Lebesgue dominated convergence theorem;close convex set;continuous mapping;fixed point theorem
O175.25
A
1671-5934(2016)06-0014-05
2016-09-19
资金项目:广东外语外贸大学南国商学院校级科研重点课题资助(16-005A)
许兴业(1900-),男,广东普宁人,教授,理学学士,研究方向为非线性椭圆型偏微分正整解理论与应用研究.
