X射线图像灰度值与透照厚度的定量关系

郭文明,陈宇亮

(北京邮电大学 软件学院, 北京 100876)



X射线图像灰度值与透照厚度的定量关系

郭文明,陈宇亮

(北京邮电大学 软件学院, 北京 100876)

摘要：X射线数字成像检测技术中，射线图像对于沿透照方向的厚度变化，表现为灰度值的变化，如何由灰度值的变化得到被检物体实际厚度的变化成为业内研究的重点。基于Beer定理，结合影响X射线机射线强度的因素和射线强度与数字图像的转换关系，推导出灰度值与透照厚度之间的定量关系；通过搭建试验平台，得到系列数据，对理论计算值和试验数据测量值进行了比对验证。结果表明：理论灰度值与实际测试相差误差不超过灰度满量程的±10%。

关键词：X射线;数字成像;缺陷;灰度值;定量分析

射线检测作为无损检测的主要方法之一，与其他方法相比具有直观、准确等优点。射线检测中垂直于射线透照方向的缺陷尺寸可精确测量[1]，但平行于射线透照方向的缺陷尺寸无法直接测量得到，而未焊透、根部内凹等缺陷深度的测量又是实际应用中的常见问题。

对于未焊透、根部内凹和根部咬边等缺陷的射线检测，为了确定底片黑度与厚度(缺陷深度)的关系，通常采用定制的通用槽型对比试块或小径管环焊缝专用对比试块模拟焊缝及未焊透深度，得到带缺陷和对比试块的底片。但是底片上的缺陷较小，而一般黑度计孔至少在2.5 mm以上，如何通过测量得到精确的缺陷深度成为难点。而在先进的射线数字成像检测中，由于使用了计算机和数字处理技术，使得通过计算机软件实现缺陷尺寸的准确测量成为可能。

目前针对X射线数字图像灰度值(以下简称灰度值)的研究，主要着重于分析灰度值与管电压和被测物体厚度等因素的定性关系，灰度值与各因素简单描述为简单的正比或反比关系[2-4]，而对于图像灰度值与被测物体厚度之间的关系，并没有给出明确的计算公式或对应关系。笔者通过分析Beer定律以及灰度值的相关理论，推导出精确的灰度值计算公式以及灰度值与厚度的对应关系，并通过试验测试公式的准确性。

1图像灰度值与透照厚度的定量分析

1.1　射线强度与透照厚度的关系

对于某一物质，射线穿过物质的衰减系数与物质密度、原子序数和射线能量有关，一般射线检测的衰减理论均是基于Beer定律[2]发展起来的。在现有的研究中，给出了光子与材料的各种相互作用截面参数、衰减系数、吸收系数等国际标准的数据表[5-7]，这些数据表同样验证了在理想的单色源情况下，穿过物体的衰减规律符合Beer定律，如下式：

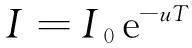
(1)

式中：μ为射线穿过单位厚度物质时的衰减系数;T为物体的厚度;I为射线透射后的强度；I0为入射射线强度。射线强度指在单位时间内、通过垂直于射线传播方向上单位面积的X射线光子的能量[8-9]。

对于X射线的照射来说，X射线管的辐射强度与管电压的平方成正比，与管电流成正比。而根据平方反比定律，强度I0与距离F的平方成反比，所以即可得出下式：

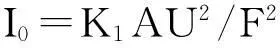
(2)

式中：K1为常数系数，可以定义为灰度值常数；A为X射线机的管电流；U为X射线机的管电压值；F为X射线机到被测物体表面的焦距距离。

由于X射线到达被检物体表面的强度与管电压、管电流、焦距有关，所以可将X射线强度看成是关于管电压、管电流、焦距的函数：

(3)

1.2　线性衰减系数的确定

1.2.1衰减系数公式

射线管电压的提高会造成射线有效能量的增加，而有效能量的增加会使射线波长变短，引起衰减系数下降[12-14]。根据光电效应、原子物理学等理论，散射和吸收截面与衰减系数存在着换算关系，但在实际检测中线性衰减系数随着工件厚度变化而发生变化，而强滤波后的射线在X射线光谱中的分布应为从最大强度附近到最短波长的范围[15]。参考文献[13] 给出了衰减系数和射线管电压之间的关系：

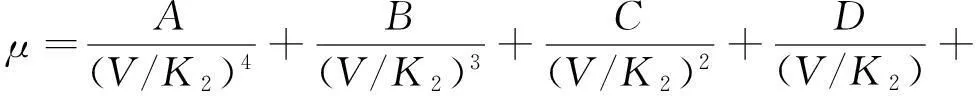
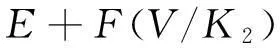
(4)

式中:A,B,C,D,E,F为常数，随透过材料的不同而不同，cm-1;V为射线的管电压;K2为常数。

1.2.2铁的衰减系数求解

求解A,B,C,D,E,F的六元一次方程,计算铁的衰减系数。其中K2与被检测材料的厚度有关,其随着材料厚度的增加而逐渐减小。在进行衰减系数测定时，对于连续谱的X射线来说会发生硬化现象，需要对衰减系数进行修正。对于给定厚度为x的衰减系数，μavex修正为理想单色源的衰减系数μave0时，需要加上修正项Δμ0;Δμ0的计算需结合Simpson公式，导出X射线修正模型的数值解法及修正方法，对修正后的衰减系数再作卷积反投影重构，即可有效消除能谱硬化造成的影响[4-5]。由于Δμ0的计算公式冗长，文章不过多展开，具体方法参照文献[5]。综合式(4)和能量谱硬化修正模型，得出铁在不同的射线管电压下，衰减系数的变化情况，具体数值如表1所示。

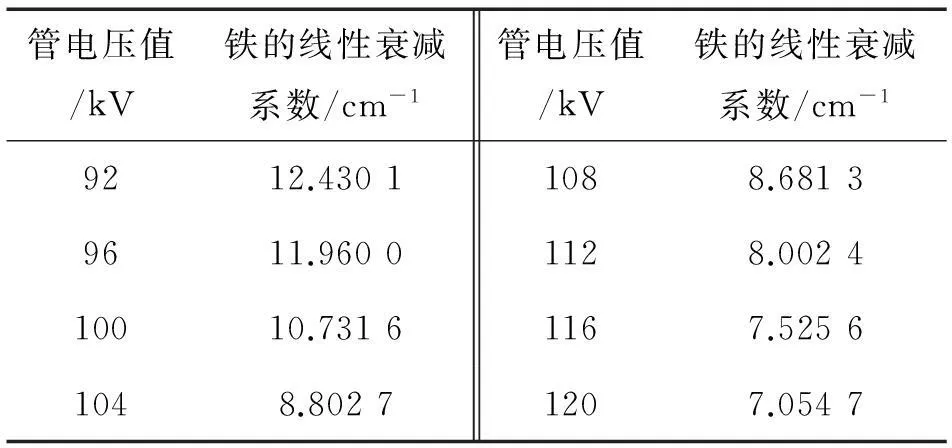
表1　铁在不同管电压下的衰减系数

从表1可看出，入射能量随着管电压增大而增大，对应的平均衰减系数减小。通过式(4)可知，被测材料的厚度增大，同样会使对应的平均衰减系数减小。这与文献[5]的研究结论相一致，说明了表1的正确性。

1.3　灰度值与射线强度的关系

射线数字图像是以灰度值的形式显示的，即需要先把X射线强度转化为数字信号(图像的灰度值)。首先，将入射X射线光子转换为电荷[10-11]，照射在像元上的X射线光子数量与像元转换的电荷数近似存在线性关系，其具体公式如下：

(5)

式中：M为光通量；R为光电变换系数。

模数转换器(A/D)将得到的电压转化为数字信号，形成数字图像[15]。模拟数字转换器的分辨率Q等于LSB电压(输出离散信号产生一个变化所需的最小输入电压的差值)：

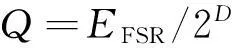
(6)

式中：EFSR为总的电压测量范围；2D为电压间隔数，D为ADC模块的精度的位数，用比特作为单位。

在上述过程中，可直接用已经量化的电压值(即比特信息)作为图像的灰度值，结合式(5)、(6)可推导出图像灰度值的变化规律：

(7)

式中：f(R0,E0,D0)为关于R0,E0,D0参数的函数；R0为光电变换系数；E0为模数转换器的转换系数；D0为灰度值位数；G为图像灰度值。

结合式(3)、(4)，可得到图像灰度值的计算公式：

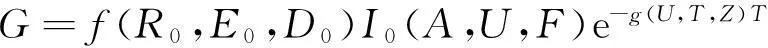
(8)

对某一检测物体来说，由于函数f(R0,E0,D0)的值与检测系统有关，在固定检测系统后，函数f(R0,E0,D0)应该是一个常数，简化为常数系数K。函数I0(A,U,F)虽然是关于射线强度的函数，但在X射线机发射器固定的情况下，可将函数I0(A,U,F)的具体形式换算成式(2)，得到试验验证公式(9)。

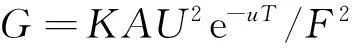
(9)

从式(9)可看出:数字图像灰度值的大小受到材料衰减系数、管电压、管电流、曝光时间和焦距的影响，同时与检测系统的硬件特性有很大关系。

2计算结果与试验验证

2.1　公式系数K求解

为了求解公式系数K，采用CMOET 225 kV X射线机和以色列vidisco非晶硅数字探测器(像素127 μm)搭建射线检测系统平台，选取不同厚度的钢板(7,10,12 mm)作为试验用试块(试块尺寸为210 mm×150 mm)，通过改变管电压，管电流和焦距来获得不同数字图像。试验主要影响因素包括管电压的不稳定和硬化现象。表2给出了钢板厚度为7 mm时，采用不同的管电压(92,95,97 kV)、管电流(5,4,3 mA)、焦距(700,800,900 mm)时得到的图像灰度值。由于衰减系数μ随着管电压而改变，故可通过查阅表1来确定衰减系数μ。将不同厚度下的管电压、管电流、焦距和图像灰度值的数值代入式(9)，可求出K值。在X射线系统固定的情况下，公式对于任何情况下的X射线都满足，那么对于上述的数据来说，K值的波动不会太大。综合另外两组厚度为10，12 mm的数据，求出K值的平均值为428.030 1。从计算结果来看，K值误差波动范围在-3.4%～3.0%之间，大体趋近一个常数。

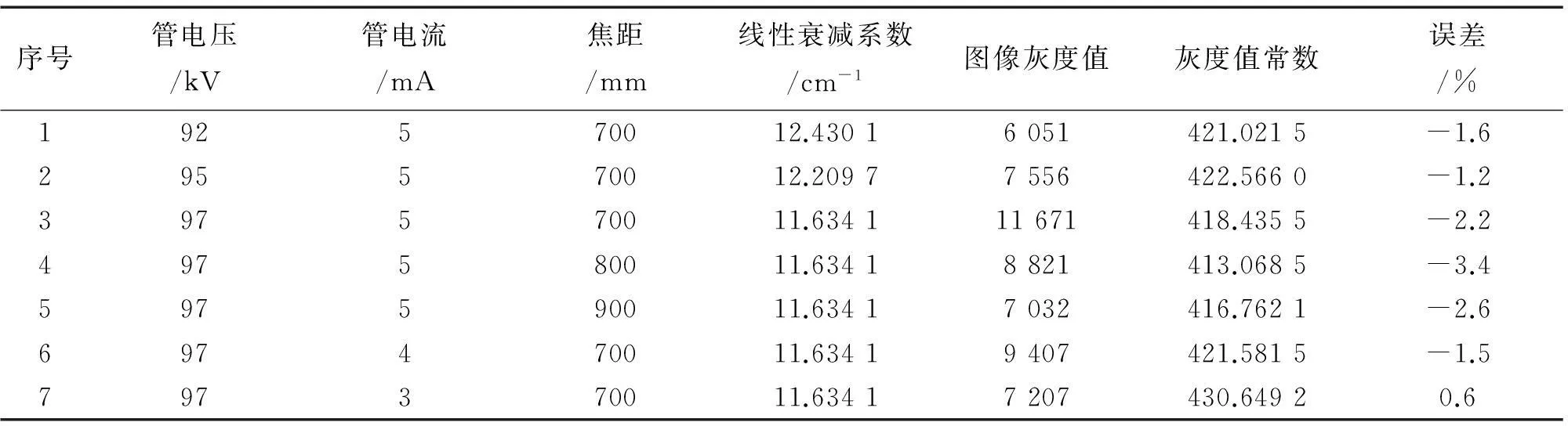
表2　不同透照条件下公式系数K的计算结果

2.2　试验验证

试验平台同上，采用管电流5 mA、焦距800 mm,改变管电压(95,100,105 kV)，对6～12 mm厚的钢制试块进行灰度值的理论计算与试验测试结果的比较。试验主要影响因素同上。结果见表3,变化趋势如图1所示。

表3　不同管电压下灰度值的试验与计算结果比较

图1　不同管电压下灰度值和透照厚度的关系曲线

从表3可看出，在运用式(9)对图像的灰度值进行计算和试验验证的过程中，在一定的透照条件下，求解得出的理论值与试验值的误差在±10%间。而从图1可看出，在管电压固定的情况下，连续计算一组数据的灰度值与试验值的曲线大致吻合。产生这种现象的主要原因有：

① 数字图像灰度值与数字射线检测系统直接相关，不同的数字探测器其响应不同，即便是同一数字探测器随着时间推移也会发生相应退化，而造成数字图像灰度值变化。② X射线机是连续的射线源，在通过修正模型对射线的硬化现象进行校正的过程中，会出现计算偏差。③ 随着钢板厚度的增加，材料的衰减系数也会发生变化，衰减系数很大程度影响了灰度值的计算。④ 式(9)中K值是通过大量试验数据求出的平均值，对于个别数据的验证仍会出现较大的误差，但是对于大量数据的验证，从图1的曲线中可以看出，试验值和计算值比较吻合。

3结论

基于射线衰减理论，分析不同透照条件下引起射线图像灰度值变化的影响因素，图像灰度值与X射线机的能量、材料的厚度和衰减系数的定量关系，推导出不同钢板厚度和图像灰度值之间的定量关系，并搭建试验平台予以验证。通过对试验得到的多组数据的分析计算表明：对于一定厚度的工件，其灰度的理论值与试验值存在一定的偏差，但在实际的射线检测中，可基于公式初步估算厚度与灰度的关系，为后续开展基于灰度值精确测量缺陷深度奠定基础。

参考文献：

[1]SIM L M, TAN T C, MON A A, et al. X-ray absorption-based technique to measure the thickness of multi-layered structures[J]. Ndt & E International, 2009, 42(4):291-296.

[2]PENG Guang-han, YANG Xue-heng, HAN Zhong, et al. Hardening correction model of energy spectrum for continuous spectrum X-ray ICT [J].Spectroscopy and Spectral Analysis,2005,25(11):1880-1883.

[3]XU Guang-duo, WANG Li-qiang, TONG Jian-min. Research on calibration model of X-ray thickness gauge[J].Atomic Energy Science and Technology,2014,5:925-929.

[4]CHEN Ping, HAN Yan, PAN Jin-xiao. Research on X-ray multispectrum imaging based on variable energy [J].Spectroscopy and Spectral Analysis,2013,32(5):1383-1387.

[5]PENG G H, CAI X H, YANG X H. Numerical analysis of hardening correction model of energy spectrum for X-ray TICT[J]. Nondestructive Testing, 2007.

[6]CULLEN D E. A simple model model of photon transport[J].Nucl InstrumMetthodsPhys Res,1995,B 101(1):499-510.

[7]KOLKOORI S, WROBEL N, ZSCHERPEL U, et al. A new X-ray backscatter imaging technique for non-destructive testing of aerospace materials[J]. Ndt & E International, 2014,70:41-52.

[8]SELTZER S M. Calculation of photon mass enery-transfer and mass enery-absorbtioncoefficient[J].Radiat Res,1993,136(2):147-170.

[9]REZA H P R, REZAIE A H, SADEGHI S H H, et al. A density-based fuzzy clustering technique for non-destructive detection of defects in materials[J]. Ndt& E International,2007,40(4):337-346.

[10]CASALTA S, DAQUINO G G, METTEN L, et al. Digital image analysis of X-ray and neutron radiography for the inspection and the monitoring of nuclear materials[J]. Ndt & E International,2003,36(5):349-355.

[11]赵肖东,蔡建刚,陈明,等. 航空零部件X射线数字成像检测系统[J]. 无损检测, 2013, 35(4):57-59.

[12]王玮,李公平,潘小东,等. 工业CT锥束X射线能谱及强度的分布模拟[J].无损检测,2014,36(3):9-13.

[13]冯长春,周炜. X射线衰减系数与射线管电压的关系初探[J].无损探伤,1997,19(1):11-13.

[14]高阔,于虹,郭铁桥. 射线数字成像(DR)技术在电力工业检测中的应用[J]. 无损检测, 2013, 35(11):76-78.

[15]连广，王庭魁.材中X射线衰减规律的验证及吸收系数测定[J].林业科技，1990(6):28-30.

Quantitative Relationship between Gray Value of X-ray Image and Radiographic Thickness

GUO Wen-ming, CHEN Yu-liang

(School of Software Engineering,Beijing University of Posts and Telecommunications, Beijing 100876,China)

Abstract：In the technology of X-ray digital imaging detection, the X-ray imaging shows changes in gray value for thickness variations along the transillumination direction. The way how to get the object's actual thickness changes by grey value change becomes the focus of the research. In this paper, based on Beer theorem and combining with the factors influencing the intensity of X-ray machine and ray intensity and digital image transformation relations, the quantitative relationship between the grey value and thickness is deduced. By setting up the experimental platform to get series of experimental data, the theoretical calculation value and experimentally measured values are compared to verify. The results show that the difference between theoretical gray value and actual grey value is not more than gray full range of ±10%.

Key words:X-ray; Digital imaging; Detection; Gray value; Quantitative analysis

中图分类号：TG115.28

文献标志码：A

文章编号：1000-6656(2016)02-0014-04

DOI:10.11973/wsjc201602004

作者简介：郭文明(1967-),男,副教授,主要从事图像处理的教学与科研工作。

基金项目：国家重大科学仪器设备开发专项资助项目(2013YQ240803)

收稿日期：2015-06-23