用于航天器微振动分析的扰源解耦加载方法

邹元杰 王泽宇 葛东明

(北京空间飞行器总体设计部，北京 100094)

用于航天器微振动分析的扰源解耦加载方法

邹元杰 王泽宇 葛东明

(北京空间飞行器总体设计部，北京 100094)

微振动源与航天器主结构之间存在耦合作用，其建模与加载方法直接影响系统级微振动分析结果。文章通过理论推导和证明，提出了一种新的微振动源精确解耦加载方法，使扰源的加载处理不受微振动源与航天器主结构耦合作用的影响，实现了扰动外载荷与航天器结构的解耦，所获取的微振动响应与系统级耦合分析结果完全相同。理论研究和数值算例表明：此方法避免了微振动源与航天器主结构的耦合分析，结果准确可靠，适用于动量轮、控制力矩陀螺等常见的扰源加载，且易于工程实施。

航天器；微振动；扰源；解耦加载

1 引言

随着高性能航天器的发展，在轨微振动问题备受关注[1-2]。航天器在轨微小振动将对空间科学试验、激光通信、光学遥感等任务产生影响，其中动量轮与控制力矩陀螺是重要的扰动源。由于微振动源本身是柔性结构，扰动力(矩)加载于航天器主结构的实际效果也会受到航天器主结构动态特性的影响，因此，通常须要开展扰源与航天器主结构的耦合分析。然而，由于扰源自身特性较为复杂，同时航天器主结构的有限元模型规模较大，开展耦合分析从理论到技术实现都有一定难度[3-6]。微振动源的建模与加载方法对于系统级微振动分析而言是最为重要的输入条件，多年来一直是国内外的研究热点之一。国内外的学者很早就对扰动源开展了测量工作，研究发现部件转动引起的扰动会被自身结构放大[7-8]。为了去除这种影响，根据文献[9]提出的扰动谐波经验模型，文献[10-11]利用试验数据辨识出相关参数，拟合出不同转速下的扰动力(矩)谐波参数进行扰动分析。文献[12-13]利用动态质量方法对测量得到的扰动力(矩)进行修正，修正后的数据可反映扰源与航天器结构的耦合特性，其修正系数可通过有限元分析或者试验测量得到。文献[14]针对柔性夹具影响，研究了微振动源界面力(力矩)测试结果的补偿方法，通过研究认为扰源在固定界面下的测试结果可以用于系统级微振动分析，这种处理没有误差，但其证明基于克雷格-班普顿(Craig-Bampton)方法，理论上并不十分严格，并且没有给出试验或数值验证。

为了准确反映扰动源与航天器的耦合作用，本文在文献[14]的基础上，通过推导结构动力学方程，揭示了干扰力在扰源-测量界面-航天器主结构组合系统内的传递规律，提出了一种微振动源解耦加载方法，利用有限元动力学方程进行了严格证明，并结合典型扰源和航天器结构进行了数值仿真验证。

2 微振动源的解耦加载方法

2.1 固支边界条件下的微振动源动力学方程

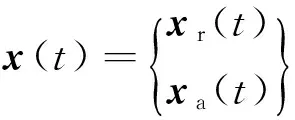
图1 固支边界条件下的微振动源系统Fig.1 Micro-vibration source system under fixed boundary conditions

微振动源的结构动力学方程表示为

(1)

式中：M、C、K分别代表质量、阻尼与刚度矩阵，下标“r”和“a”分别代表界面以外的内部自由度和界面自由度。

在频域下，方程可转化为

(2)

式中：ω为振动圆频率，xr、xa、Fr、Fa分别表示xr(t)、xa(t)、Fr(t)和Fa(t)对应的频域复数量。

为了简化表达式，定义分块动刚度矩阵：

(3)

式中：下标p和q表示分块矩阵Z的对应行和列。按照式(3)所述的分块动刚度矩阵定义方式，式(2)可简化记为如下形式：

(4)

由于固定界面下，xa=0，代入式(4)，因此，可得固定界面处的干扰力为

(5)

式中：Zar和Zrr为式(4)左侧相应位置的动刚度分块矩阵。

2.2 微振动源与航天器主结构的耦合动力学方程

为了准确描述微振动源与航天器主结构的耦合动力学特性，本节建立耦合动力学方程，后文将以耦合分析为基准验证解耦加载方法的有效性。“微振动源+航天器主结构”耦合系统如图2所示。

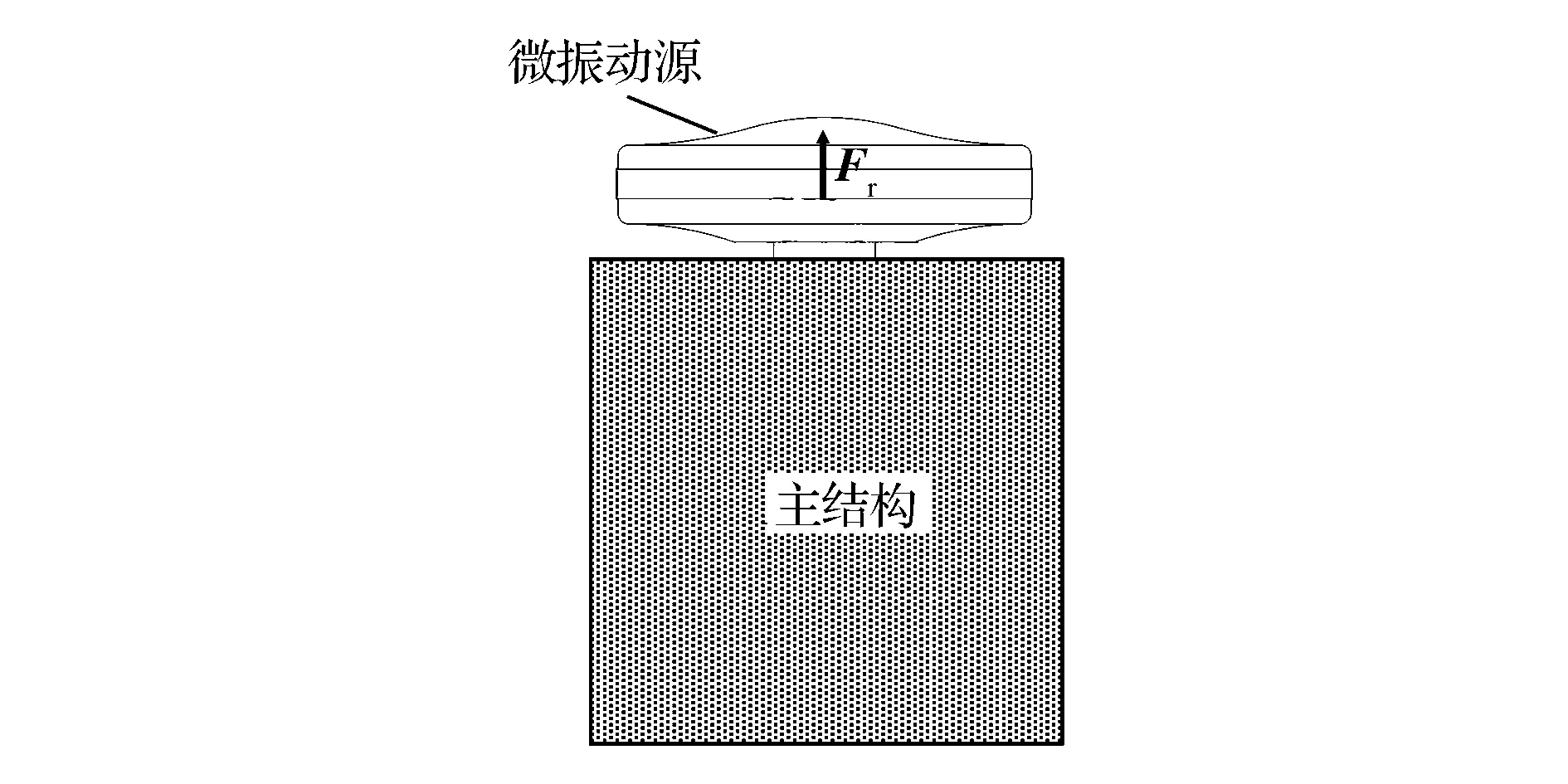
图2 “微振动源+航天器主结构”耦合系统Fig.2 Coupled assembly system of micro-vibration sources and spacecraft main-structures

沿用2.1节分块动刚度矩阵的定义，“微振动源+航天器主结构”耦合系统的频域动力学方程表述为

(6)

由式(6)可得

(7)

(8)

(9)

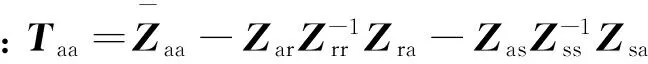
2.3 微振动源的解耦加载方法

本节推导解耦加载方法的动力学方程，通过和2.2节耦合分析方程进行对比，从理论上说明方法的准确性。微振动源解耦加载系统如图3所示。

图3 微振动源解耦加载系统Fig.3 Decoupled loading system of micro-vibration sources

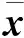
(10)

由式(10)，并代入式(5)的Fa可得

(11)

(12)

(13)

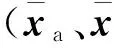
须要说明的是：①由于式(4)、式(6)和式(10)左端的系数矩阵不要求对称，因此，转子部分可以考虑陀螺响应(转子部分的系数矩阵为反对称阵)，也就是说，在考虑陀螺效应的情况下，上述解耦建模方法仍适用；②上述推导针对组合系统的自由-自由状态，若整星系统在悬吊或者地面弹性支撑状态或者固支下进行，其基本的动力学方程形式仍可归结为式(6)和式(10)，因此，上述理论仍然成立，也就是说，上面的理论证明适用于任意边界条件的整星结构系统。

3 数值分析结果

3.1 解耦加载方法的数值仿真验证

首先，对解耦加载方法进行数值仿真验证。假设动量轮因动静不平衡产生的干扰力(矩)为6个方向单位力(矩)，相位为0，分别采用解耦加载和系统级耦合分析方法进行计算。为了便于输出界面力和力矩，动量轮与航天器主结构连接界面用刚性多点约束(MPC)连接到卫星本体1个节点(见图4)。其中，解耦加载方法首先将动量轮动静不平衡干扰力(矩)施加于动量轮顶部某节点上，计算固支边界条件的界面合力(矩)，而后，将获取的界面合力(矩)加载于动量轮与主结构连接界面节点，计算组合系统的响应；而系统级耦合分析则直接将干扰力(矩)施加于动量轮某节点上，计算组合系统的响应。

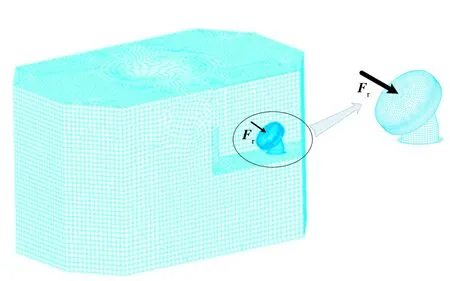
图4 结构有限元模型Fig.4 Finite element model of structures

计算时为了避免引入模态叠加的误差，采用有限元矩阵直接求解方法，计算频率范围为5～500 Hz，结构阻尼系数取为1%。具体分析方法和流程见文献[1]。

动量轮安装界面点、航天器主结构节点和动量轮内部节点的平动加速度(Ax、Ay、Az)和转动加速度(Rx、Ry、Rz)响应曲线分别见图5～图7。从图中可见，使用本文提出的解耦分析方法得到动量轮安装界面节点响应、航天器主结构节点响应与系统级耦合分析结果完全一致，但动量轮内部节点响应计算结果与耦合分析结果差异较大(仅在低频段接近)。这说明除微振动源内部节点外，本文方法可精确计算微振动源-航天器主结构组合系统的响应。

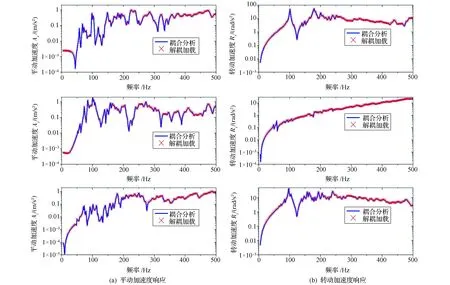
图5 动量轮安装界面点加速度响应Fig.5 Acceleration at installation node of RWA

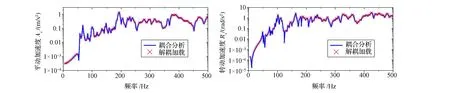
图6 航天器主结构节点加速度响应Fig.6 Acceleration at node of spacecraft main structure

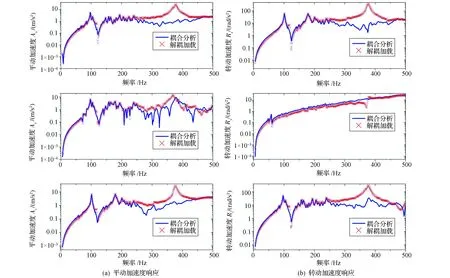
图7 动量轮内部节点的加速度响应Fig.7 Acceleration at internal node of RWA structure

3.2 动量轮采用集中质量模型的影响分析

由于工程中在进行整星(器)微振动分析时，常将动量轮和控制力矩陀螺的扰源简化为集中质量(惯量)来处理，本节对比动量轮有限元模型与动量轮集中质量模型的差异，以把握这种工程处理的误差大小。计算时建立了2个整星模型，其主结构模型完全相同，动量轮部分分别采用有限元模型和集中质量模型。2个模型的输入载荷均为3.1节所述的动量轮固支边界下的界面力-Fa，采用解耦加载的方式施加于动量轮安装界面节点。

图8、图9给出了将动量轮简化为质心处的集中质量后的计算结果，从对比结果看，动量轮集中质量模型和动量轮有限元模型的响应曲线峰值位置与随频率变化规律不同，部分频段的峰值相差1～2个数量级。因此，从本算例的对比情况看，将动量轮等微振动源简化为集中质量模型，误差较大。建议在进行整星(器)微振动分析时要建立完整的扰源有限元模型。

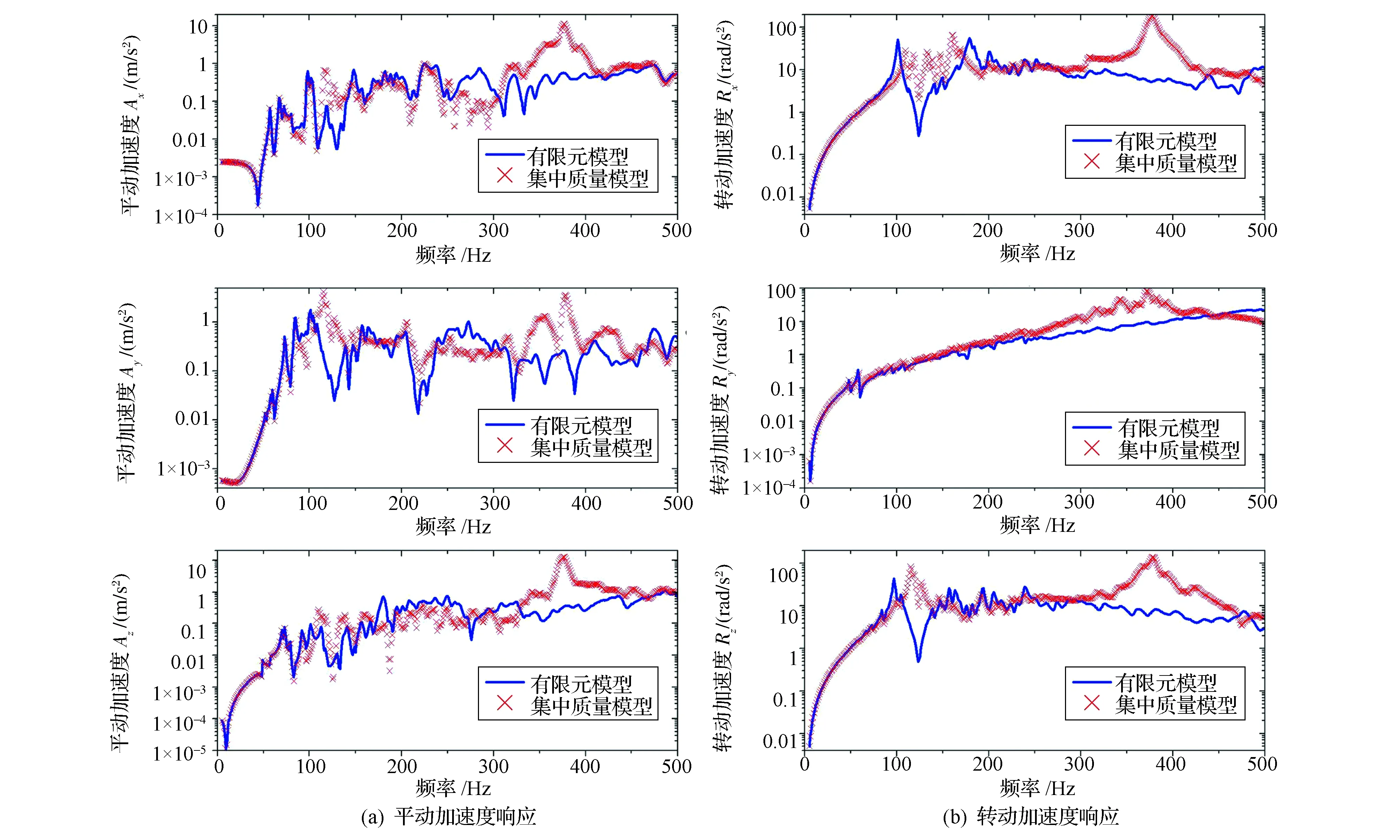
图8 两种动量轮模型的加速度响应对比(动量轮安装界面点)Fig.8 Accelerations by two RWA models at installation node of RWA

图9 两种动量轮模型的加速度响应对比(主结构节点)Fig.9 Accelerations by two RWA models at node of spacecraft main structure

4 结论

本文通过理论推导与数值仿真研究，得到以下结论：

(1)提取旋转部件干扰力(矩)对其固定安装界面的作用力(矩)加载到微振动源-航天器主结构组合系统(微振动源的安装界面)，所得到的航天器主结构响应即是真实的耦合响应，在理论上严格准确。因此，微振动源的界面力仅需在固定界面下获取，而后加载在完整系统上，从而实现了微振动源的解耦建模与加载，使得耦合问题的数值分析大大简化。该方法适合多扰源情况，适用于任意航天器边界条件，并可考虑转子陀螺效应。

(2)研究成果具有一般性，不仅可以解决在轨微振动预示问题，还可推广用于处理复杂的器箭动力学问题。例如，运载火箭或航天器在新型发动机作用下的动响应预示是有一定难度的，因为箭(器)主结构和发动机存在耦合作用，发动机的实际扰动力通常很难直接测量得到。按照本文的研究结果，可以将发动机与其安装结构组装在一起，开机试车测试其固定安装界面(即与箭(器)系统其他结构的分界面)作用力，然后将该作用力加载于系统完整的模型上，即可准确预示发动机及其安装结构以外的动态响应。这种处理避免了复杂的发动机扰动力直接测量或辨识。

(3)将动量轮等微振动源简化为集中质量模型，误差较大，因此，建议在进行整星(器)微振动分析时要建立完整的扰源有限元模型。

(4)本文的方法须要提供扰源自身的有限元模型，后续应进一步研究扰源有限元模型的不确定性对响应预示精度的影响，并开展扰源有限元模型的修正方法研究。

References)

[1] 邹元杰,王泽宇,张志娟,等. 航天器微振动稳态时域响应分析方法[J].航天器工程,2012,21(6):37-42

Zou Yuanjie,Wang Zeyu,Zhang Zhijuan,et al. Analysis method of steady time-domain response for spacecraft micro-vibration[J]. Spacecraft Engineering,2012,21(6):37-42 (in Chinese)

[2]王泽宇，邹元杰，焦安超，等. 某遥感卫星平台的微振动试验研究[J].航天器环境工程，2015,32(3)：278-285

Wang Zeyu,Zou Yuanjie,Jiao Anchao,et al. The jitter measurement and analysis for a remote sensing satellite platform[J]. Spacecraft Environment Engineering,2015,32(3)：278-285 (in Chinese)

[3]葛东明,邹元杰,张志娟,等. 基于全柔性卫星模型的控制闭环微振动建模与仿真[J].航天器工程，2012,21(5): 58-63

Ge Dongming,Zou Yuanjie,Zhang Zhijuan,et al. Control closed-loop micro-vibration modeling and simulation based on flexible satellite model[J]. Spacecraft Engineering,2012,21(5): 58-63 (in Chinese)

[4]葛东明，邹元杰. 高分辨率卫星结构-控制-光学一体化建模与微振动响应分析[J].航天器环境工程，2013,30(6)：586-590

Ge Dongming,Zou Yuanjie. Structure-control-optics integrated modeling and micro-vibration analysis for high resolution satellite[J].Spacecraft Environment Engineering,2013,30(6)：586-590 (in Chinese)

[5]董瑶海. 航天器微振动-理论与实践[M]. 北京: 中国宇航出版社,2015

Dong Yaohai. Spacecraft mirco vibration theory and application[M].Beijing: China Astronautics Press,2015 (in Chinese)

[6]Eyerman C E. A system engineering approach to disturbance minimization for spacecraft utilizing controlled structures technology[D]. Cambridge：Master Dissertation of Massachusetts Institute of Technology,1990

[7]赵煜，张鹏飞，程伟. 反作用轮扰动特性测量及研究[J]. 实验力学,2009,24(6)：532-538

Zhao Yu,Zhang Pengfei,Cheng Wei. Measurement and study of disturbance characteristics of reaction wheel assembly[J]. Journal of Experimental Mechanics,2009,24(6)：532-538 (in Chinese)

[8]Bialke B. A compilation of reaction wheel induced spacecraft disturbances[C]//AAS Guidance and Control Conference. San Diego,CA:AAS,1997

[9]Masterson R A,Miller D W. Development and validation of empirical and analytical reaction wheel disturbance models[D]. Cambridge：Master Dissertation of Massachusetts Institute of Technology,1999

[10] Uebelhart S A. Conditioning,reduction,and disturbance analysis of large order integrated models for space-based telescopes[D]. Cambridge：Master Dissertation of Massachusetts Institute of Technology,2001

[11]Liu K,Maghami P,Blaurock C. Reaction wheel disturbance modeling,jitter analysis,and validation tests for solar dynamics observatory [C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Washington D.C.: AIAA,2008

[12]Elias L M,Miller D W. A coupled disturbance analysis method using dynamic mass measurement techniques[C]//43rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Washington D.C.: AIAA,2002

[13]Elias L M,Dekens F G,Basdogan I,et al. A methodology for ‘modeling’ the mechanical interaction between a reaction wheel and a flexible structure[C]//Interferometry in Space,Bellingham: SPIE,2003: 541-555

[14]Wang Guangyuan,Zhao Yu,Zheng Gangtie. Frequency domain compensation method for moving part disturbance measurement[C]//Proceedings of 13th European Conference on Spacecraft Structures,Materials & Environmental Testing. Paris：ESA，2014

(编辑：李多)

Decoupled Loading Method of Disturbance Sources for Spacecraft Micro-vibration Analysis

ZOU Yuanjie WANG Zeyu GE Dongming

(Beijing Institute of Spacecraft System Engineering,Beijing 100094,China)

Since micro-vibration sources and spacecraft main structures are coupled,how to model and load the disturbance would severely impact the results of the systematic micro-vibration analysis.A new decoupled loading method of disturbance sources is presented in this paper with theoretical derivation and verification,which realizes the decoupling of disturbance sources and spacecraft structures and makes it unnecessary to consider the coupling effects between disturbance sources and main structures. It is shown by the theoretical study and numerical computations,that this method could avoid the complex coupling analysis of disturbance sources and main structures,and that it is accurate and simple to be applied for common disturbance sources such as reaction wheels and control moment gyros.

spacecraft; micro-vibration; disturbance source; decoupled loading

2016-05-03；

2016-05-13

国家重大科技专项工程

邹元杰，男，研究员，从事航天器力学环境预示、动力学与控制研究工作。Email：yuanjiez@qq.com。

V414；V417

A

10.3969/j.issn.1673-8748.2016.04.007