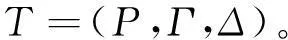基于k-定界的动态下推网络可达性分析



基于k-定界的动态下推网络可达性分析

引文格式： 徐力，钱俊彦.基于k-定界的动态下推网络可达性分析[J].桂林电子科技大学学报,2016,36(1):48-51.

徐力，钱俊彦

(桂林电子科技大学 计算机科学与工程学院，广西 桂林541004)

摘要：为了保证含有递归、动态创建线程并发系统的安全性，提出基于动态下推网络模型的形式化验证方法。该模型的可达性为不可判定，把动态下推网络转换为在k-定界下可达性可判定的下推网络，再将转换后的下推网络符号化。分析表明，该方法可使模型可达性成为可判定的，且缓解了模型状态空间爆炸的状态。

关键词：动态下推网络；k-定界；可达性分析；符号化

随着多核技术的发展以及内存容量越来越大，基于充分利用资源的原则，Java语言引入Fork/Join并行模式，通过该模式，并发程序可把线程分解成更细粒度的子线程并行执行[1]，且动态创建新线程[2]对构造系统组件具有重要意义，如在程序执行过程中，可创建新线程，实现函数回调。但由于并发线程交错执行，使得代码中隐匿的漏洞和错误难以检测。

为保证带动态线程创建和含有递归的并发程序运行安全，采用动态下推网络[3]对其进行模型检测。然而，动态下推网络可达性不可判定[4]，使得验证难以实现。Qadeer等[5]提出了k-定界可达算法，解决了多栈下推系统的上下文模型检测，但无法解决带动态线程创建的可达性问题。

鉴于此，基于k-定界技术，将动态下推网络模拟成可达性可判定[6]的下推网络，并基于下推网络提出一种符号下推网络可达算法[7]，压缩状态空间来缓解爆炸问题的状态。

1相关知识

1.1并发程序并行模式

随着大规模数据处理的与日俱增以及硬件价格的大幅下降，高性能多核并发计算得到广泛应用，基于多核技术的并行编程语言及编程模式被广泛运用。例如，Java在第7版中引入Fork/Join并行模式，以及被广泛使用Map Reduce并行编程模式等。通常程序在运行时，若其线程池中的一个线程正在执行某个任务，由于资源不足或者其他原因，无法继续执行，则该线程会挂起处于等待中。基于Fork/Join并行框架的程序，若处理某个任务的线程无法执行，该线程会主动寻找其他尚未运行的子问题执行，Fork/Join并行编程技术可减少线程等待时间，充分利用处理器资源，提高程序性能。

图1中的父线程能否执行，依赖于其子线程的执行结果，只有当其子线程执行结束，调用线程才能获得父线程返回结果。Fork/Join并行模式运行的基本原理为：当连接一个客户时，使用Fork创建一个线程标识符，存储在一个变量中，该新线程标识符会被拷贝到父线程的标识符变量中，该新线程是原线程的副本，可与客户完成通信。在该线程运行结束，返回父线程继续执行的过程中，该变量包含的线程标识符一直被Join操作监视[8]。

图1　Fork/Join并行模式Fig.1　Fork/Join model

1.2动态下推网络

动态下推网络M由一组动态下推系统[9-10]

{D1,…,Di,…,Dn} s.t.i1≤i≤n

组成。其中：Di=(Pi,Γi,Δi)为一个动态下推系统；Pi为状态集；Γi为栈字符集；Δi为迁移规则集合，具有以下形式：

1)pia→pjωj，其中pjωj∈Pj×Γj*为动态创建的新线程；

2)pia→piωi▷pjωj， s.t.pi,pi∈Pi,a∈Γi,ωi∈Γi*。

动态下推网络是一组下推系统，并行执行各自顺序序列的迁移系统。每个下推系统都可执行下推操作，以及在网络中动态创建线程。假定G为全局变量集，动态下推系统格局可表示为

(g,p,ω)∈G×(P×Γ*)，

其中g∈G为全局变量，元组p,ω=p1,ω1,…,pi,ωi,…,pn,ωn，每个子项pi,ωi∈P×Γ*表示一个下推线程的局部格局。

定义1一个动态下推网络可表示为一个六元组M=(G,P,Γ,Δ,gin,γin)。其中：G为所有全局变量赋值的集；P为所有局部控制状态集合；Γ为所有栈字符集合；Δ为任意线程迁移关系集合；gin为初始全局状态；γin为初始局部状态(栈内容)。

以下给出了一个伪代码程序，详细阐述用动态下推网络建模的格局迁移。

Main() {Initamend(){ Amend(){

1: call Initamend5: create Amend7: write data

2: write data6: return8: return

3: read data } }

4: return

}

用pi表示第i行代码的程序状态，a表示栈顶字符，其中pi∈P,a∈Γ。迁移关系集合为:

其中φi∈Δ表示迁移路径。设开始格局集合为β1={p1a},目标格局集合为β2={p8ap3a}，可知从格局集合β1到格局集合β2可达，其可达路径集合为

1.3动态下推网络可达性问题

2k-定界可达问题描述及算法

假设一个迁移系统M和一个格局γ，如果格局γ在系统M中可达，当且仅当存在一条从初始格局γin到目标格局γ的路径，即γin→*Mγ。动态下推网络可达性问题已被证明是不可判定的，但是，如果在分析可达性问题时，对迁移中的上下文切换次数进行限定，可使得该问题变得可判定。对于给出的限制切换次数的正整数k，可递归定义的格局γ上的k-定界迁移关系：

其中：→i表示新的迁移关系；→*i表示该迁移关系的传递闭包。对于正整数k，因为每一个新迁移关系的闭包→*i都可能产生无限多种迁移，使得一个格局可迁移到无限多个不同的格局，所以，k-定界状态空间和迁移序列可能是无界的。

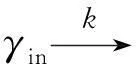
Qadeer等[5]提出k-定界可达算法，主要为解决多栈下推系统的上下文模型检测。该算法通过迭代增加执行上下文数目，其中，在单个执行上下文内，当前线程对于全局变量处于锁定状态，只有当前线程才能访问全局状态。只有执行上下文切换时对该全局状态进行同步更新，这样其他线程才能共享全局状态信息。具体的k-定界可达算法如下：

输入：并发下推系统C=(G,Γ,Δ0,…,Δn,gin,ωin)；正整数k。

输出：Reach。

1letAin=(Q,G,d, {gin},F)

//其中L(Ain)={gin, ωin}

2WorkList∶={(g,Ain,…,Ain, 0)};

//包含N+1个Ain

3Reach∶={g,Ain,…,Ain};

4while(!WorkList)

5let(g,Ain,…,Ain,i)=REMOVE(WorkList)in

6if(i

7forall(j=0,…,N)

11ADD(WorkList, (x,i+1));

12Reach:=Reach∪{x};

13}

k-定界可达算法中第1~3行分别表示对自动机、工作线程及可达集合的初始化，从第4行开始，针对工作线程WorkList，穷尽计算并发下推系统C中小于k-定界切换的格局。对于并发下推系统C=(G, Γ,Δ0,…,Δn, gin, ωin)和给定的正整数k，该算法是可终止的，其复杂度为O(k3(N|G|)k|P|5)。

3基于下推网络符号化分析

3.1转换为下推网络

给定一个动态下推网络M=(G, P, Γ, Δ, gin,γin)和一个正整数k，可模拟一个对应的下推网络M。模拟转换的基本思想为：对动态下推网络进行k-定界上下文切换的限制，即执行一步迁移最多有k个不同的线程。因此,下推网络可使用标识符为{0,1,…,k-1}的线程迁移递归地来模拟动态下推网络的迁移，约定标识符为k的线程从不执行迁移，用来模拟动态下推网络的剩余线程。最终通过转换得到的下推网络包含k+1个线程，其局部状态表示为(p, n, a)。其中：p为局部变量；n为执行迁移线程对应最大线程标识符；a为终止线程对应线程标识符。转换算法如下：

输入：动态下推网络M=(G, P,Γ, Δ, gin, ωin)；正整数k。

输出：对于下推网络M′。

1lett=0;//标识符初始化为0

2WorkList∶=g,(p, 0,a),γ;

//包含N+1个Ain

3forall(p, 0,a),γ∈WorkListdo

//选择一个线程为n的初始状态，开始构造

4if(0<=t<=n&&n

5forallΔ

6switch(Δ)

7begin

8casep,γ→p′,γ′∈Δ;

9Move(p,n,a),γ→(p′,n,a),γ′

intoΔ′;break;

10caseg,p,γ→g′,p′,γ′∈Δ;

11Moveg,(p,n,a),γ→g′,(p′,n,a),γ′intoΔ′;break;

12casep,γ→p′,γ′p″,γ″∈Δ;

13Move(p,n,a),γ→(p′,n,a),γ′

intoΔ′;break;

14WorkList∶=(p″, ++n,a),γ″;break;

15caseg,p,γ→g′,p′,γ′p″,γ″∈Δ;

16Moveg,(p,n,a),γ→g′,(p′,n,a),γ′intoΔ′;break;

17WorkList∶=(p″, ++n,a),γ″;break;

18casep,γ→$;

19Move(p,n,a),γ→(p′,n,a∪{t}),$intoΔ′;break;

20endswitch；

20t++;//下一个线程

转换算法中第1~2行分别表示对标识符和工作线程初始化，从第3行开始，针对M的格局迁移关系，穷尽计算下推网络M的迁移关系。由算法可知，当标识符t=k或无新的迁移规则时，执行终止，该算法的时间复杂度与程序的大小呈指数关系，与多项式整数k呈线性关系。

3.2符号化分析

转换后的下推网络由一组不能进行动态创建线程的下推系统组成，为了描述方便，只描述单个下推系统进行符号化的过程，下推网络符号化与之类似。

下推系统

其中：P为控制位集；Γ为栈字符集；Δ⊆(P×Γ)×(P×Γ*)为迁移关系集。

符号下推系统

其中G和L为整数{0,1}集合。

符号迁移函数

简化表示为

其中：R⊆(G×L)×(G×Ln)；(g, l, g, l1, l2,…,ln)∈R。

下推系统T和符号下推系统Ts对程序中赋值语句、函数调用以及返回语句的建模规则定义如下：

2)程序调用。T的迁移规则为g, (n1,l)→g, (n3,l) (n2,l)，Ts的迁移规则为p,n1p,n3n2。

3)返回语句。T的迁移规则为g, (n1,l)→g,ε，Ts的迁移规则为p,n1p,ε。

由迁移规则可知，符号下推系统Ts比下推系统T的表达更紧凑、简洁，且程序中的布尔变量和整数值都可用OBDD表示，可以指数性地压缩状态空间，以便节省大量搜索时间。

4结束语

针对Fork/Join并行性的并发程序，用动态下推网络进行建模，并利用k-定界和符号技术缓解空间爆炸问题的状态，其算法效率有待改进。下一步研究方向主要为：

1)针对Fork/Join并行性的实时并发系统，基于该模型引入能刻画时间行为的时钟，构造时间动态下推网络，并基于时钟模型提出相应的可达搜索算法。

2)利用现有的模型验证工具(如Moped)，实现并发递归系统的抽象模型验证，解决位向量、语言决策等问题。在现有工具的基础上，利用相关求解算法,开发相应的实时并发程序的验证工具。

参考文献:

[1]TAUBENFELD G.A closer look at concurrent data structures and algorithms[J].Bulletin of the European Association for Theoretical Computer Science,2015,115:61-82.

[2]SONGF,TOUILIT.Modelcheckingdynamicpushdownnetworks[C]//SHANCC.Proceedingsofthe11thAsianSymposiumonProgrammingLanguagesandSystems:8301Melbourme,Australia,2013:33-49.

[3]ATIGM,BOUAJJANIA,QADEERS.Context-boundedanalysisforconcurrentprogramswithdynamiccreationofthreads[C]//Proceedingsofthe15thInternationalConferenceonTACASLNCS5505,UnivYork,EuropeanAssoc,2009:107-123.

[4]RAMALIANGAMG.Contextsensitivesynchronizationsensitiveanalysisisundecidable[J].OnProgrammingLanguagesandSystems,2000,22:416-430.

[5]QADEERS,REHOFJ.Context-boundedmodelcheckingofconcurrentsoftware[C]//HALBWACHSN,ZUCKLD.11thInternationalConferenceonToolsandAlgorithmsfortheConstructionandAnalysisofSystems:3440.Edinburgh:Springer,2005:93-107.

[6]MCLEAND,RYBAKOVV.Multi-agenttemporarylogicTS4(Kn)(U)basedatnon-lineartimeandimitatinguncertaintyviaagents'interaction[C]//RUTKOWSKIL.LectureNotesinArtificialIntelligence.LNCS8052.Zakopane,POLAND,2013:375-384.

[7]ESPARZAJ,SCHWOONS.ABDD-basedmodelcheckerforrecursiveprograms[C]//BERRYG,COMONH,FINKELA.13thTnternationalConferenceonComputerAidedVerification:2102.Heidelberg:Springer,2005:93-107.

[8]BOLLIGB,KUSKED,MENNICKER.Thecomplexityofmodelcheckingmulti-stacksystems[C]//Proceedingsofthe28thAnnualACM/IEEESymposiumonLogicinComputerScience,NewOrleans,LA,USA,2013:163-72.

[9]LAMMICHP,OLMM,SEIDLH.Contextuallockingfordynamicpushdownnetworks[C]//Proceedingsofthe20thInternationalSymposiumonStaticAnalysis,Seattle,WA,USA,2013:47-98.

[10]CAOXiaojuan,MIZUHITOD.Well-structuredpushdownsystems[C]//MELGRATTIH.LecturenotesinArtificialIntelligence.LNCS8052,Berlin,Heidelberg:Springer,2013:121-136.

编辑：梁王欢

Research onk-delimited accessibility analysis for dynamic pushdown network

XU Li， QIAN Junyan

(School of Computer Science and Engineering, Guilin University of Electronic Technology, Guilin 541004, China)

Abstract：In order to ensure the security of concurrent system which contains recursion and dynamic creating threads, the formal verification method based on dynamic pushdown network model is proposed. The accessibility of this model is undecidable. The dynamic pushdown network is transformed into the accessibility which can be decidable under the k-delimited condition. And then the transformed pushdown network is symbolized. The analysis shows that the method makes the accessibility of the model decidable and greatly optimizes the problem of model state space explosion.

Key words：dynamic pushdown network; k-delimited; accessibility analysis; symbolic

中图分类号：TP301

文献标志码：A

文章编号：1673-808X(2016)01-0048-04

通信作者：钱俊彦(1973-)，男，浙江嵊县人，教授，博士，研究方向为形式化方法、模型检测。E-mail：junyanq@gmail.com

基金项目：国家自然科学基金(61262008)；广西自然科学基金(2012GXNSFAA053220,2014GXNSFAA118365)

收稿日期：2015-04-06