一类有理-三角样条曲线
2016-03-15马虹,彭丰富
一类有理-三角样条曲线
引文格式: 马虹,彭丰富.一类有理-三角样条曲线[J].桂林电子科技大学学报,2016,36(1):52-55.
马虹,彭丰富
(桂林电子科技大学 数学与计算科学学院,广西 桂林541004)
摘要:为了构造一种代数-有理多项式与三角函数相结合的参数曲线,基于代数-三角混合函数空间构造参数曲线曲面的理论,运用有理参数曲面的生成方法,把代数-三角混合多项式应用到有理多项式样条中,构造了一类有理-三角样条曲线,对该曲线的性质及构造方法进行了研究。有理-三角多项式作为有理多项式的推广,在插值和逼近上比多项式更具有灵活性和有效性,而且在曲线曲面形状的控制方面具有很好的应用。此类曲线是摆线的广义情形,具有良好的端点性质和插值多样性。
关键词:曲线;代数三角混合多项式;有理-三角函数
曲线曲面造型技术对计算机辅助几何设计具有非常重要的研究意义,在构造参数曲线曲面时一般以多项式为基函数,样条函数自发展以来经历了Ferguson曲线、Bézier曲线、B样条曲线和有理B样条曲线,现在应用比较广泛的是非均匀有理B样条(NURBS)曲线[1-3]。B样条和NURBS具有表示与设计曲线曲面的很多优点,但是仍然存在一些问题。例如,B样条对于一些二次曲线曲面只能近似地予以表示;NURBS的有理形式虽然可以精确地表示二次曲面,但其有理形式也使计算变得复杂;Bézier方法推进了曲线曲面的设计,但是对曲线的控制性存在不足[4-6]。代数-三角多项式样条函数可以克服某些曲线不能精确表示的缺点。张纪文[7]提出了均匀节点的C-曲线概念。2001年,Mainar等[8]在代数三角混合函数空间中提出了规范B基的构造,所构造的曲线曲面不仅具有插值性、光顺性和局部可调性等优点,而且在适当的条件下还可以精确表示二次曲线曲面。近年来,用代数三角混合多项式表示参数曲线曲面成为了一种崭新的方法,吕勇刚等[9]在扩展的代数三角混合函数空间中提出了k阶代数三角多项式样条。
有理多项式样条函数既是有理逼近的重要组成部分,又是多项式样条的推广,兼顾了二者的优点,更具一般性和灵活性。为此,将有理多项式与代数-三角多项式样条相结合,构造了一类有理-三角平面曲线,并分析了其相关性质。
1有理-三角平面曲线

平面内的m次有理曲线可以用参数方程对其进行表示[11]:
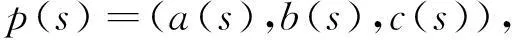
(1)
其中a(s),b(s),c(s)∈R[s],且max(deg(a),deg(b),deg(c))=m。
空间n次有理曲线的参数方程为
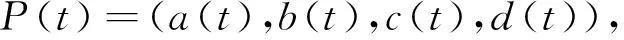
(2)
其中a(t),b(t),c(t),d(t)∈R[t],且max(deg(a),deg(b),deg(c),deg(d))=n[11]。
一般情况下,为了讨论方便,式(2)中的前3项可以写成齐次形式P(t)=(a(t),b(t),c(t)),其表示为一空间曲线,其中gcd(a,b,c)=1[11]。同样P(t)的次数定义为:
deg(P(t))=max(deg(a),deg(b),deg(c))。
(3)
类似地,有理参数曲面可表示为:
通常写成齐次形式:
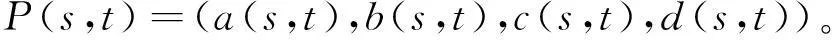
其中a,b,c,d∈R[s,t],且gcd(a,b,c,d)=1[10]。
根据有理曲面的构造方法,由平面内m次有理曲线P(s)=(A(s),B(s),C(s))及空间n次有理曲线P(t)=(a(t),b(t),c(t),d(t)),可生成一个双阶(m,n)的空间曲面[12],
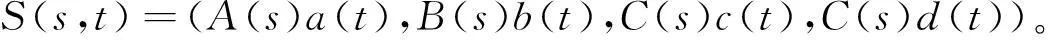
(4)
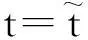
类似地,利用这种方法就可得到一类有理-三角样条曲线。由平面曲线Q(θ)=(θ-sinθ,1-cosθ,1)与P(t)=(1,1,1/r(t))可以生成空间曲线S(θ,t):
(5)
其中,1/r(t)为多项式,t∈R+。
由式(5)的同态形式,若定义t与θ的一个函数关系,从而可以得到平面曲线
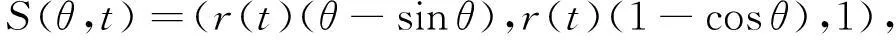
(6)
即在欧几里德空间中有参数曲线:
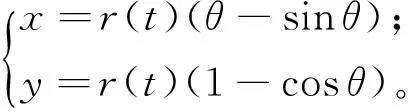
(7)
这里,定义t与θ的关系
(8)
对式(8)两边积分,
(9)
令r为有理多项式,
(10)
代入式(9),得
(11)
2曲线性质
构造的有理-三角平面曲线(7),若令r(t)为常数即为摆线,其几何意义为:当一个圆在一条直线上作不滑动的滚动时,圆周上的点所描绘的旋轮线称为摆线。滚动圆半径r为关于参数t的有理多项式,t∈[0,1];θ为圆的半径滚动经过的角度,θ∈[0,2π]。当θ从0变动到2π时,动圆上一定点就刻画出广义摆线。
在有理多项式(10)中,如当m=5,
(12)
代入式(11)得
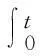
(13)
取广义摆线上的任意6点:p1(0.007 9,0.037 2),p2(0.132 8,0.186 2),p3(0.402 3,0.256 1),p4(0.256 4,0.018 4),p5(0.710 4,0.047 1),p6(1.196 1,0.000 6),通过插值可得到动圆半径及摆线图形。

r(t)具有如下性质:
1)正性。r(t)≥0。
2)单调性。有理多项式r(t)和其一阶导数r′(t)的图像分别为图1、2。从图1、2可看出,其单调性为:当t∈[0,0.5)时,r(t)单调递减;当t∈(0.5,1]时,r(t)单调递增。
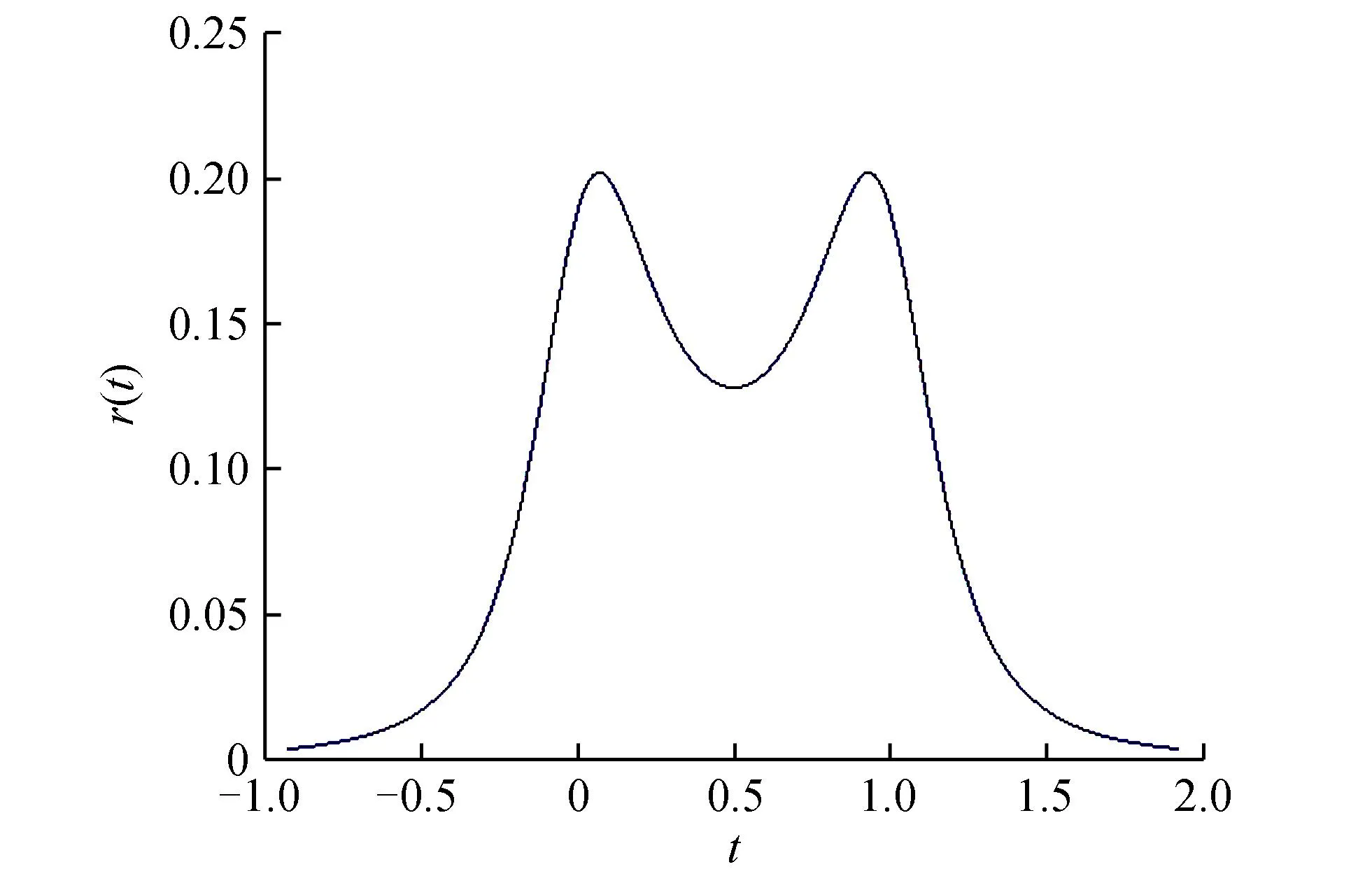
图1 有理多项式曲线Fig.1 Rational polynomial curve

图2 有理多项式一阶导数曲线Fig.2 First derivative curve of rational polynomial
3)存在性。广义摆线中,对于一组精确的数值点通过插值法求解其对应方程组有解,节点对应的参数也是明确的。这一性质使得构造的曲线具有插值多样性,且满足光顺的要求。
所构造的有理-三角多项式样条曲线具有如下性质:
1)端点性质。有理-三角样条曲线在t∈[0,1]区间具有良好的端点性质,图像经过首末两端点,如图3所示。
2)单调性。当t∈[0,0.5]时,曲线单调递增;当t∈[0.5,1]时,曲线单调递减。
3)拼接性。有理-三角样条曲线在端点处一阶导数连续,具有很好的拼接性,如图4所示。

图3 有理-三角多项式曲线Fig.3 Rational-trigonometric polynomial curve

图4 有理-三角多项式一阶导数曲线Fig.4 First derivative curve of rational-trigonometricpolynomial
3结束语
为了构造一种代数有理-三角有理多项式与三角函数相结合的参数曲线,构造了一类有理-三角样条曲线,这类曲线一方面继承了多项式样条曲线的优点,另一方面描述与设计的曲线曲面具有较好的插值性、光顺性、形状可调节性。另外,有理形式的三角多项式样条曲线能精确表示一些二次曲线曲面,在研究曲线曲面的应用上有较好的实用价值。通过增加一个坐标系,可推广到空间曲线的构造。
参考文献:
[1]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001:306-454.
[2]苏本跃.基于三角多项式曲线曲面的几何造型理论与方法研究[D].合肥:合肥工业大学,2007:18-71.
[3]李军成,赵东标,杨炼.拟三次三角样条插值曲线与曲面[J].小型微型计算机系统,2013,3(3):680-684.
[4]PIEGL,TILLERM.TheNURBSBook[M].2nded.Berlin:Springer,1997:141-188.
[5]苏本跃,盛敏.代数三角混合Bézier型插值曲线[J].工程图学学报,2010,31(6):39-44.
[6]HANXu’an.ThecubictrigonometricBéziercurvewithtwoshapeparameters[J].AppliedMathematicsLetters,2009,22(2):226-231.
[7]ZHANGJiwen.C-curves:anextensionofcubiccurves[J].ComputerAidedGeometricDesign,1996,13(9):199-217.
[8]MAINARE,PENAJM.AbasisofC-Béziersplineswithoptimalproperties[J].ComputerAidedGeometricDesign,2002,19(8):291-295.
[9]吕勇刚,汪国昭,杨勋年.均匀三角多项式样条曲线[J].中国科学(E辑),2002,32(2):281-288.
[10]史晓冉.μ基的应用-空间曲线奇异点的计算及有理曲面的隐式化[D].合肥:中国科学技术大学,2012:14-105.
[11]贾晓红.有理曲线与曲面的μ基理论[D].合肥:合肥工业大学,2009:20-129.
[12]SHIXiaoran.Usingmovingplanestoimplicitizerationalsurfacesgeneratedfromaplanarcurveandaspacecurve[J].ComputerAidedGeometricDesign,2014,31(9):631-641.
编辑:翁史振
A type of rational-trigonometric curve
MA Hong, PENG Fengfu
(School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China)
Abstract:In order to construct a kind of parametric curve combined with algebraic-rational polynomial and trigonometric function, based on the theory of constructing parametric curve and surface in the algebraic-trigonometric blending function space, by using the rational parametric surface generating method, the algebraic-trigonometric blending polynomial is applied to rational polynomial splines for constructing a type of rational-trigonometric curve. The nature and construction method of the curve is studied. As the promotion of rational polynomial, the rational-trigonometric polynomial is more flexible and effective in interpolation and approximation, and has a good application on controlling curve and surface. This kind of curve is a generalized case of cycloid with good endpoint property and interpolation diversity.
Key words:curve; algebraic-trigonometric polynomial; rational-trigonometric function
中图分类号:TP391
文献标志码:A
文章编号:1673-808X(2016)01-0052-04
通信作者:彭丰富(1972-),男,湖南双峰人,副教授,博士,研究方向为计算机辅助几何设计。E-mail:pengfengfu@aliyun.com
基金项目:广西自然科学基金(2015GXNSFAA139014)
收稿日期:2015-10-08
