引入界面传热系数后铸型厚度与蓄热能力关系

王启才,陈 玲,高卫国

(1.天津理工大学 天津市复杂系统控制理论及应用重点实验室，天津 300384；2.天津理工大学 机械工程学院，天津 300384)

引入界面传热系数后铸型厚度与蓄热能力关系

王启才1,2,陈 玲1,2,高卫国1,2

(1.天津理工大学 天津市复杂系统控制理论及应用重点实验室，天津 300384；2.天津理工大学 机械工程学院，天津 300384)

采用硅铝合金(含Si 13.5%)为铸件材料，45号钢为铸型材料，引入铸造数值模拟重要的边界条件界面传热系数，同时改变铸型厚度，利用有限元分析软件ANSYS模拟了金属铸造过程温度场的分布规律，分析了铸型厚度变化对铸造温度场分布的影响。结果表明：引入界面传热系数可提高数值模拟的准确性；增加铸型壁厚可提高铸件凝固速度，当铸型壁厚增加到一定厚度后，对凝固速度的影响减弱以至消失。

ANSYS；金属铸造；界面传热系数；有限元分析；温度场

0 前言

虽然铸造CAE(铸件充型和凝固过程计算机仿真)在提高铸件质量，缩短设计周期以及优化铸造工艺方面已经应用于铸造行业[1]，但随着机械工业的发展，铸件的结构变得越来越复杂，对铸造产品的质量要求也就更高。因此，如何在实际铸造前有效的模拟铸造过程，预测铸件缺陷和提高模拟精度等诸多问题都是目前研究的重点问题[2,3]。

铸造时影响铸件温度场分布的因素较多，如：铸型厚度、材料类型、铸型蓄热能力、界面传热系数等等[4,5]。在这些影响模拟精度的因素中，首推界面传热系数，在数值模拟中引入该系数可以提高模拟的准确性，但是模拟中如何引入界面传热系数也不是一件容易的事。因此很多研究者忽略了铸件和铸型之间的接触状态是变化的这一重要因素，模拟的精度有待商榷[6-7]。

本文引用文献[6]中的界面传热系数与时间关系的表达式：h(t)=a(t)b，h为热阻R的倒数。该表达式是金属型铸造时，假设初始时刻金属液体充满铸型，结晶潜热采用热焓法处理，并用反算法得出的[6,7]。本文在模拟时考虑界面传热系数，利用该界面传热系数公式，采用数学方法求出对应的待定系数a和b。

又因为铸型蓄热能力是影响金属充型能力、激冷能力、温度梯度、热应力大小、温度场分布的重要参数，而铸型厚度变化对铸型蓄热能力有直接影响[8]，以本文利用ANSYS软件模拟厚度对铸造温度场分布的影响，并将模拟结果与实验数据对比，研究得出铸型厚度、温度、时间之间关系曲线，为研究铸型厚度对铸造温度场的影响提供了有力的依据。

1 实验设计及瞬态温度场有限元计算

1.1 实验模型及几何尺寸

实验铸件材料为硅铝合金，浇铸温度650 ℃，制成边长为100 mm的正方体。铸型材料为45钢，制成13种形状，第一种是边长为130 mm的立方体，各面厚度均为15 mm[6]；第二种是边长为135 mm，各边厚度均为17.5 mm；依此类推，铸型厚度x每次增加2.5 mm，即xi=15,17.5,20,……,42.5,45；i=1,2,3, ……,13。由于篇幅有限，文中仅列出x1=15mm时铸型示意图，图1中#1、#2、#3为温度测量点，也是热电偶测量通道，具体位置如图2所示。

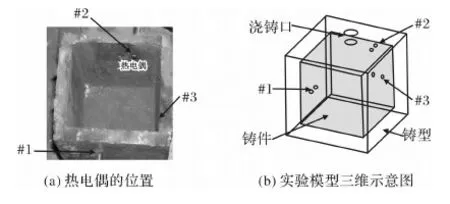
图1 热电偶放置及三维模型示意图Fig.1 The positions of thermocouples and 3D model diagram

图2 实验模型示意图Fig.2 Schematic chart of test model

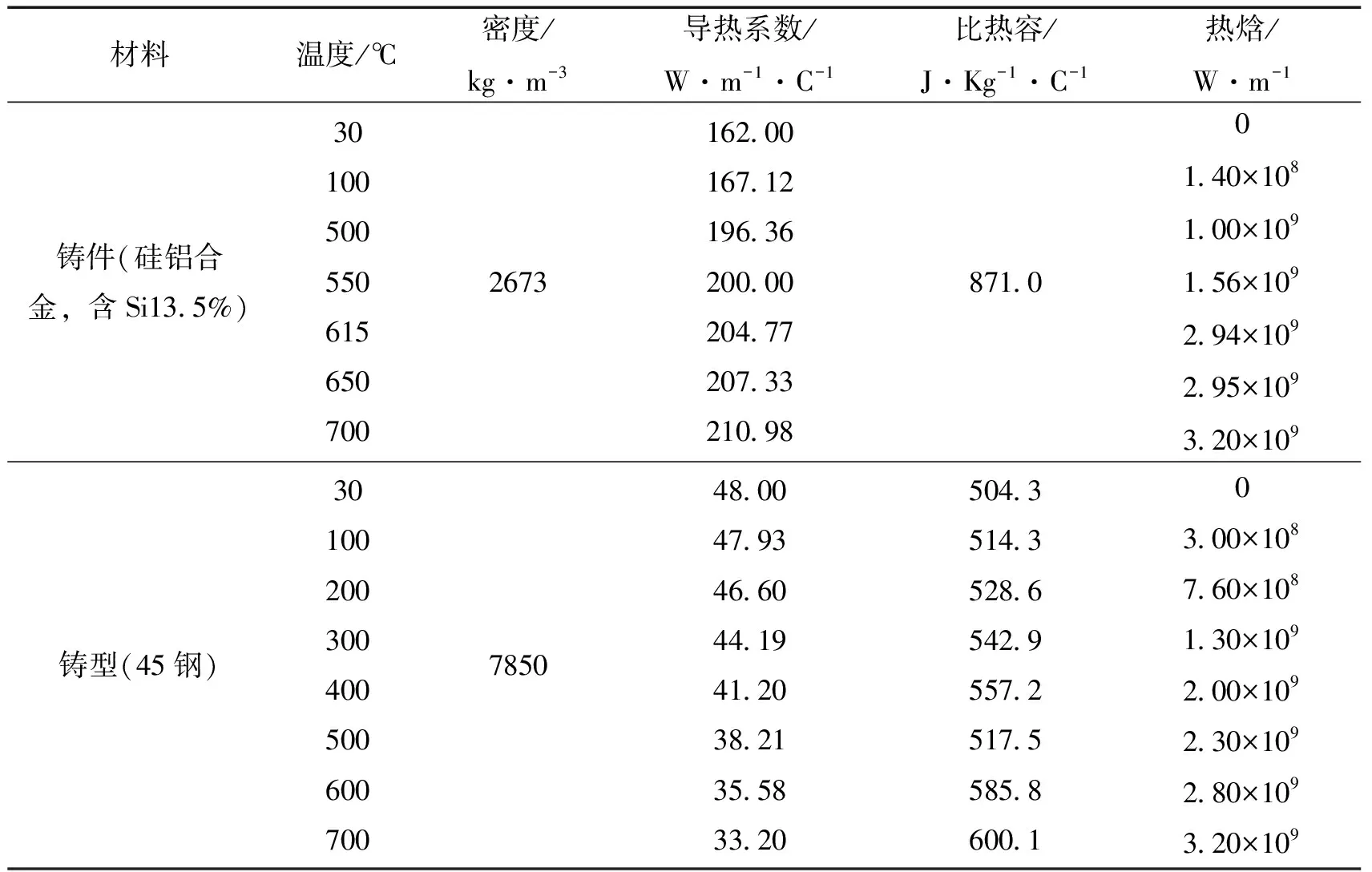
材料温度/℃密度/kg·m-3导热系数/W·m-1·C-1比热容/J·Kg-1·C-1热焓/W·m-1铸件(硅铝合金，含Si135%)3010050055061565070026731620016712196362000020477207332109887100140×108100×109156×109294×109295×109320×109铸型(45钢)30100200300400500600700785048004793466044194120382135583320504351435286542955725175585860010300×108760×108130×109200×109230×109280×109320×109

1.2 材料物性参数及铸型表面空气换热系数

本文采用材料物性参数来自文献[6]铸件为硅铝合金，熔点615 ℃，凝固点550 ℃；铸型为45号钢，如表1所示。铸型表面空气换热系数上表面k1=20，四周k2=20，下表面k3=30，W·(m·℃)-1

1.3 引入界面传热系数并建立有限元模型

实际铸造凝固过程中铸型体积膨胀铸件收缩使得铸件与铸型之间形成了空气间隙，产生热阻并阻碍热量的传递，如果在计算中仍假设100%的理想接触导致数值模拟结果与实验结果存在较大误差，为提高数值模拟准确性，本文模拟过程中考虑接触单元和引入界面传热系数[6,9]。

图3是铸型厚度x1=15mm有限元模型及接触对，(a)图采用八节点六面体的Solid70划分的铸件网格，(b)图采用Conta175和Targe170形成接触对；共有12044个单元,其中10362个Solid 70单元, 350个Conta 175单元, 1332个Targe 170单元。

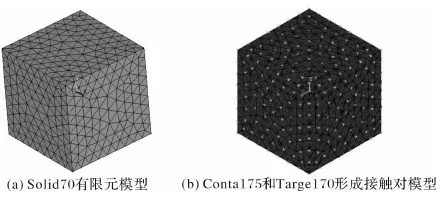
图3 铸型厚度x1=15mm有限元模型及接触对Fig.3 Finite element model and contact pairs of mold thickness at x1=15 mm

2 模拟结果分析

2.1 实验数据处理和模拟结果对比分析

为对比模拟与实验结果，针对同一个实验模型做了多次实验，应用粗大误差判据理论处理实验数据，图4是铸型厚度x1=15 mm时观测点2与观测点2对应铸件节点103和铸型对应节点2533的温度随时间变化曲线。

从图4可看出，引入界面传热系数后观测点2实验曲线与模拟曲线相近，且相对误差es都在5%以内，与工程实际情况相符合。验证了引入界面传热系数后模型的准确性，为下一步铸型厚度变化分析打下基础。

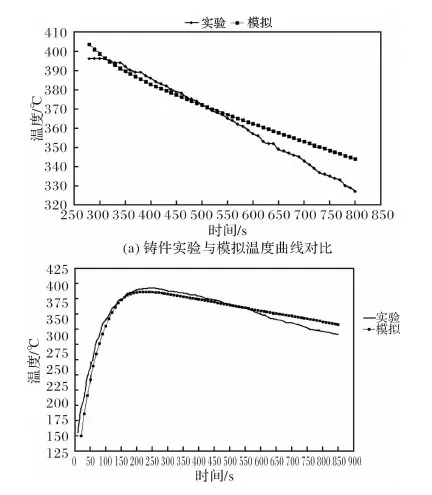
图4 铸型厚度x1=15 mm时观测点2与模拟温度曲线对比图Fig.4 Comparison between curves of the observed points 2 and the simulated temperature while the mold thickness at x1=15 mm

2.2 铸型厚度对铸造温度场分布影响分析

图5是铸件在100 s和1 800 s时的温度场分

图5 铸型厚度x1=15 mm铸件温度场分布图Fig.5 Temperature distribution of the mold thickness at x1=15 mm

布云图。从图中可以看出，铸型棱边厚度变化对铸件表面中心处温度影响最小，所以选取铸件表面接近正中心处Node 260，Node 368，Node 479的求解结果进行分析，如图6和图7所示。

图6 三节点空间位置 Fig.6 The position in space of three nodes

图7 三节点温度随时间变化图Fig.7 Variation of temperature of three nodes

图8以Node 260为例，随着铸型厚度的增加，铸件的降温速度变大，尤其当厚度xi从15 mm到22.5 mm时，降温幅度最为明显，而当xi从22.5 mm到45 mm时，铸型厚度对铸件温度影响变小，与文献[8]叙述相一致。进一步分析同时间段各曲线变化率，时间从0 s到100 s时，厚度xi对应温度/时间曲线变化率几乎一致；当时间从100 s递增到400 s时，厚度xi对应温度/时间曲线变化率随着铸型厚度的增加而增大；当时间从400 s递增到1 800 s时，厚度xi对应温/时间度曲线变化率受铸型厚度影响不大。根据模拟结果可以对铸型蓄热能力做出相应的改变，即对铸型厚度进行优化设计，从而得到符合设计要求的铸件[10]。

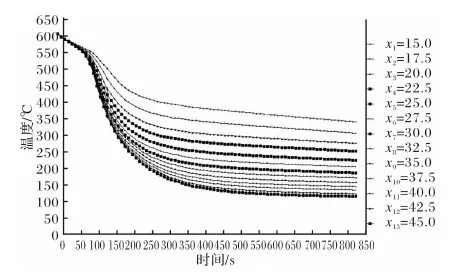
图8 节点260不同铸型厚度下温度随时间变化曲线对比Fig.8 Comparison among the temperature of variation curves of 260 node with different casting thickness

3 结论

(1)在金属铸造数值模拟时，引入界面传热系数可提高模拟三维精度，是不可忽视的参数。

(2)铸件冷却主要取决于铸型的蓄热能力，增加铸型壁厚可提高铸件冷却速度，当铸型壁厚增加到一定厚度后，对凝固速度的影响减弱以至消失。

[1] 王君卿，孙逊. MCSP6-2004国际会议概况和铸造过程数值模拟技术发展动向[J].铸造，2005,54 (4): 307-313.

[2] Ohnaka I, Sugiyama A, Zhu J D et al. Recent development and challenges of CAE in casting. In: J-Z. J, Yao S, Hao H et al., eds. Proceedings of Modeling of Casting and Solidification Processes VII[C]. Dalian, China: Dalian University of Technology Press, 2007:3-8.

[3] 傅骏，方辉，蔺虹宾. ANSYS在高职《铸造工艺学》教学中的应用[J]. 铸造技术，2013，34(1)：92-94.

[4] 李俊文，赵海东，吴朝忠. A356铝合金挤压铸造界面传热系数的研究[J]. 特种铸造及有色合金，2014，34(3)：269-272.

[5] 竹励萍，陈玲.采用非线性估算法对铸造界面传热系数的研究[J].武汉大学学报(工学版), 2009，42(2)：268-272.

[6] 竹励萍.金属型铸型铸造凝固过程铸件/铸型界面换热系数的研究[D].天津理工大学, 2009.

[7] 夏巍.铝合金重力铸造过程中铸件-模具界面换热系数反求及其在仿真中的应用[D].湖南大学，2013.

[8] 戴斌煜，王薇薇.金属液态成型原理[M].北京：国防工业出版社，2010.

[9] 徐戎，李落星，张立强,等. 金属型铸造界面换热系数峰值预测模型的建立和验证[J]. 中国有色金属学报，2014，24(4)：950-957.

[10]张立强.凝固界面换热系数反求及铝合金薄壁件低压铸造工艺优化[D].湖南大学，2011.

The relationship of the mold thickness with thermal storage capacity after introducing the interfacial heat transfer coefficient

WANG Qi-cai1, 2, CHEN Ling1, 2, GAO Wei-guo1, 2

(1.Tianjin Key Laboratory for Control Theory & Applications in Complicated Systems,Tianjin University of Technology, Tianjin 300384, China;
2. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China)

In the follow experiment, this paper used silicon aluminum alloy (containing 13.5% Si) as casting material. And 45 steel as mold material. The interfacial heat transfer coefficient, which is the important boundary condition, was introduced in numerical simulation. And the thickness of the mold was changed. The distribution regularity of the temperature field in casting solidification was simulated used the finite element software ANSYS. In addition, it also changed the casting thickness of the mold to analyze the effect of the distribution of casting temperature field. Finally the results indicate that the numerical simulation accuracy can be improved by introducing the interfacial heat transfer coefficient. Furthermore, the solidification rate can be improved by raising the casting thickness of the mold. In the process of the numerical simulation, when the mold wall-thickness was increased to a certain thickness, the affection was mitigated and almost eliminated.

ANSYS; metal casting; interfacial heat transfer coefficient; finite element analysis; temperature field

2015-11-18；

2015-12-14

大学生创新创业训练计划项目(201410060034)

王启才(1991-)，男，研究方向：计算机辅助工程分析。

TG115.25

A

1001-196X(2016)04-0040-04