合作博弈在硫化车间生产调度中的应用研究*

胡乃平　张立英

(青岛科技大学信息科学技术学院　青岛　266042)



合作博弈在硫化车间生产调度中的应用研究*

胡乃平张立英

(青岛科技大学信息科学技术学院青岛266042)

摘要针对轮胎加工生产过程中硫化车间的生产调度成本问题,基于客户成本需求,建立基于合作博弈的生产调度模型,设计采用自适应遗传算法对模型进行求解,达到降低硫化车间生产成本的目的。实验仿真结果证明了该模型的有效性和可行性。该方法的应用相对于普通生产调度,能够更有效地减少车间成本。

关键词合作博弈; 硫化车间; 生产调度; 生产成本

Production Scheduling of Vulcanization Workshop Based on Cooperative Game

HU NaipingZHANG Liying

(School of Information Science & Technology, Qingdao University of Science and Technology, Qingdao266042)

AbstractFor costs of production scheduling in tire curing workshop production processes based on customers’ demands, a cooperative model based on lowering production costs vulcanization workshop is built. Adaptive genetic algorithm is adopted to solve this model to reduce production costs. Simulation experiments show that this model is effective and feasible. Application of this method for production scheduling, can more effectively reduce costs than other methods.

Key Wordscooperative game, curing workshop, production scheduling, production costs

Class NumberTP272

1引言

硫化车间生产调度问题是一类经典的有多约束条件和多优化指标要求的、关于稀少的生产资源能否合理分配的问题,它是一类复杂的生产调度问题[1~2]。在硫化车间中生产资源的有限性使得传统的硫化车间调度方法通常只考虑客户之间竞争有限资源的问题,很少有考虑客户之间以合作的方式来解决调度中的问题[3]。目前国内外对生产调度的研究日益关注,博弈也逐渐被用来解决生产调度问题[4~6]。合作博弈也因此逐渐被用在生产调度中解决调度问题[7~8]。

本文基于硫化车间的生产调度问题,针对轮胎硫化车间生产的现状以及轮胎加工生产过程中硫化车间的生产调度,拟从合作博弈理论的基本原理入手,研究客户之间以合作的方式建立联盟,构建硫化车间相关的生产调度合作博弈模型,将成型车间看作是需要硫化半成品轮胎的客户,基于客户的成本需求,将多个客户的待硫化任务映射成博弈中的局中人,待硫化任务可选的硫化机编号排序映射为可行策略集,将硫化车间的成本映射成硫化车间成本函数,以满足客户方的成本需求。将硫化车间的设计采用自适应遗传算法求解该模型,通过实验仿真证明该模型的正确性和有效性。

2基于合作博弈的硫化车间生产调度建模

2.1硫化车间调度问题

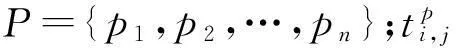
基于成本的需求,一个简单的硫化车间调度问题可描述为一个六元组,(Ni,Si,Pi,Ui,σ0,d,e),其中:

1)Ni为带硫化的轮胎半成品构成的局中人,N={J1,…,Jn};

2)Si为Ji可选的硫化机策略集合,Si可选集合{m1,m2,…,mk};

3)Pi是加工任务的加工时间向量,p=(pij)i∈Ni,j∈Si,且pij>0;

4)Ui为Ji的选择Si策略时的成本函数,若客户在交货期限内完成,则客户支出成本与完工时间成线性关系;若客户拖期,则客户支出成本需要在线性成本基础上增加拖期惩罚;

5)σ0为初始任务排序;

6)d表示加工任务的交货期集,d=(di)，i∈Ni;

7)e表示加工任务延迟交货的拖期惩罚,e=(ei),i∈Ni;

G=(S1,…,Sn;U1,…,Un)

(1)

因此硫化车间的调度问题的合作博弈模型的数学表述为

G=(Ni,Si,Pi,Ui,σ0,d,e)

N={N|1≤i≤m}

(2)

由以上定义的Ji的加工成本推知:

(3)

在本文中,拖期不交货的惩罚额度和提前完成交货任务的成本与半成品轮胎硫化的加工完工时间呈线性关系,因此可以得到拖期成本为

(4)

整个硫化任务的成本函数由Ui,1(si),Ui,2(si)构成。

由于总成本函数由Ui,1(si),Ui,2(si)两部分构成,因此归一化处理后才能简化计算。确定两部分成本的相应权重,且ω1+ω2=1,总成本函数就简化为

Ui(si)=ω1Ui,1(si)+ω1Ui,2(si)

(5)

2.2合作博弈模型的建立

硫化车间的客户采用合作机制,相互之间转让加工任务的优先权,则所有任务排序中有一个最佳排序,是合作联盟的最小加工成本[9]。所有排序为ΠN,最佳排序为σn。在上面模型描述中,最佳生产任务排序下,客户的总加工成本为由式(5)可给出。

所有客户的总加工成本为

UN=∑i∈NUi(si)(1≤i≤N)

(6)

所有客户的初始加工总成本为UN=∑i∈NUi(si)。该调度下,所有客户都有与加工时间和完工时间相关的加工成本。从全局角度看,必然有一个使所有客户的总加工成本最低的调度排序使得所有客户最终的加工成本达到最低。

各客户如果想要减少成本支出通过合作机制进行排序调整,找到全局最优的调度方案,然后再分摊全局最优调度方案带来的成本节省,因此能够使得客户自身的加工成本下降。根据上面的定义,生产调度的合作博弈模型可以定义为

(7)

V(N)表示通过客户的合作,所有客户的总成本节省。

通过定义,基于客户成本需求的硫化车间生产调度问题就转换为最大化合作博弈调度联盟的成本节省问题,能够使合作博弈调度联盟总成本节省最大的调度方案就是基于成本需求的硫化车间生产调度的最优解。

3合作博弈模型的求解

遗传算法作为一种迭代算法,经常用来求解最优问题[10]。本文为了验证所提出硫化车间合作博弈模型正确性、合理性,设计使用自适应遗传算法进行求解。由于遗传算法中影响算法行为和性能关键的是交叉概率和变异概率,而标准遗传算法中,交叉概率和变异概率是固定不变的,这直接影响算法收敛性[11]。因此本文基于自适应遗传算法能够根据每一代的结果自适应产生动态交叉概率和变异概率,从而快速地收敛的优点,设计交叉概率和变异概率参数自适应的遗传算法求解该模型。

硫化车间的合作博弈的调度模型目标是得到使硫化成本最低的调度排序,与以往的目标有所不同,因此为了满足客户和加工方的各自需要,满足客户间相互合作的新需求,需要重新设计一个新的适应度函数,设计如下

(8)

(9)

(10)

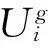
3.1实验初始化条件和参数

本文使用如下数据进行仿真实验验证。实验中假设所有客户订购了16条轮胎,有4台硫化机,相关的初始化参数如表1和表2所示。本文中,为降低后续合作博弈成本节省的分配的难度,不允许待硫化轮胎跨硫化机调整加工顺序。

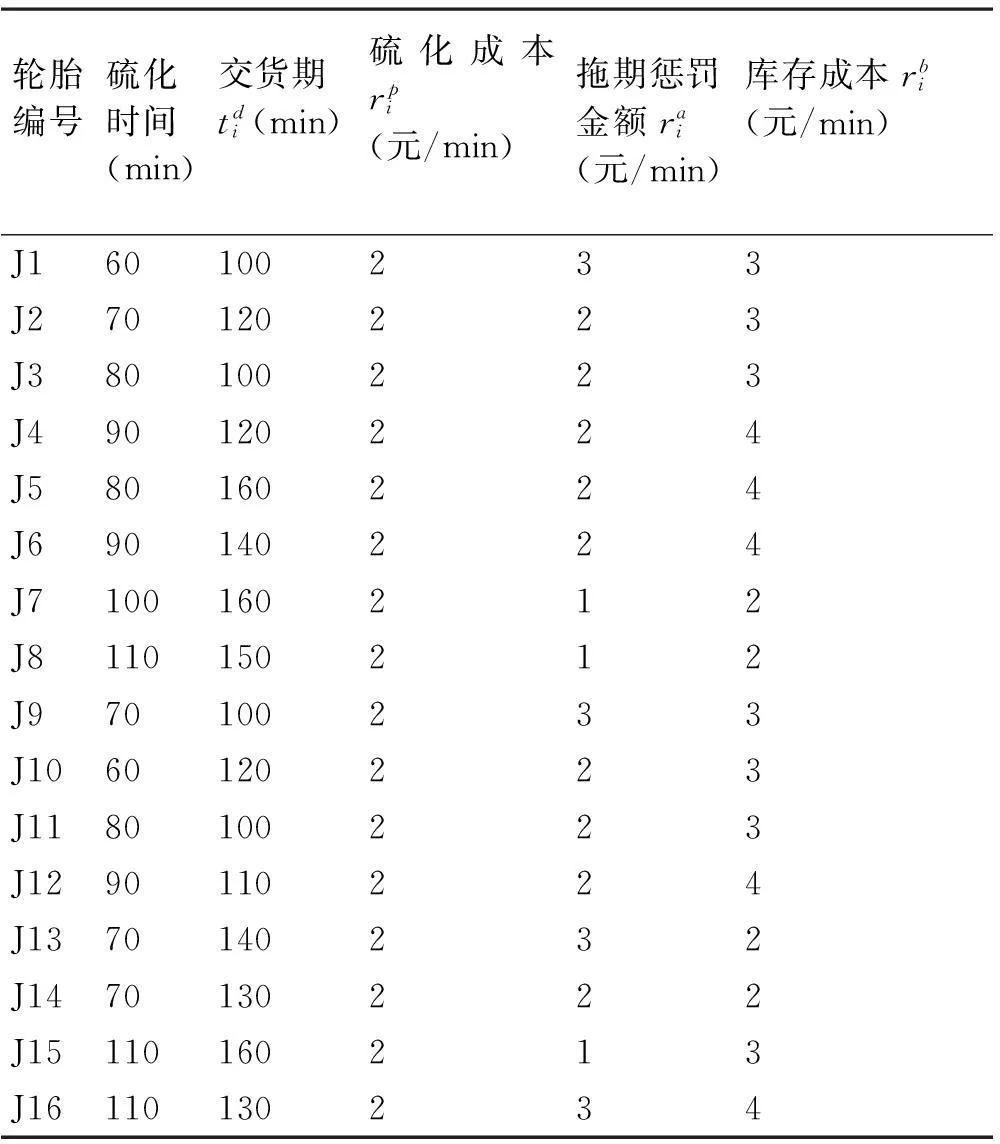
表1　硫化任务初始相关参数

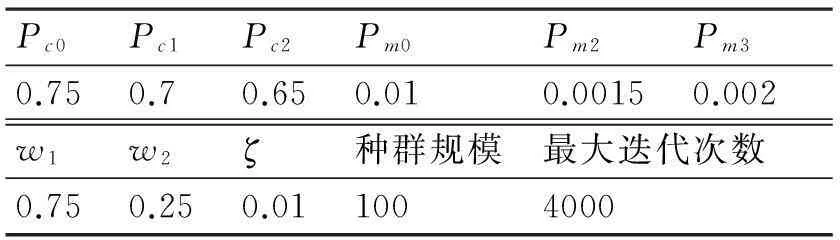
表2　遗传算法输入参数

3.2结果与分析

仿真结果如表3、表4、表5所示,表3表示遗传算法部分后代的调度结果,表4为遗传算法调度的部分代成本比较,表5为遗传算法部分代的成本节省。

表3　调度结果

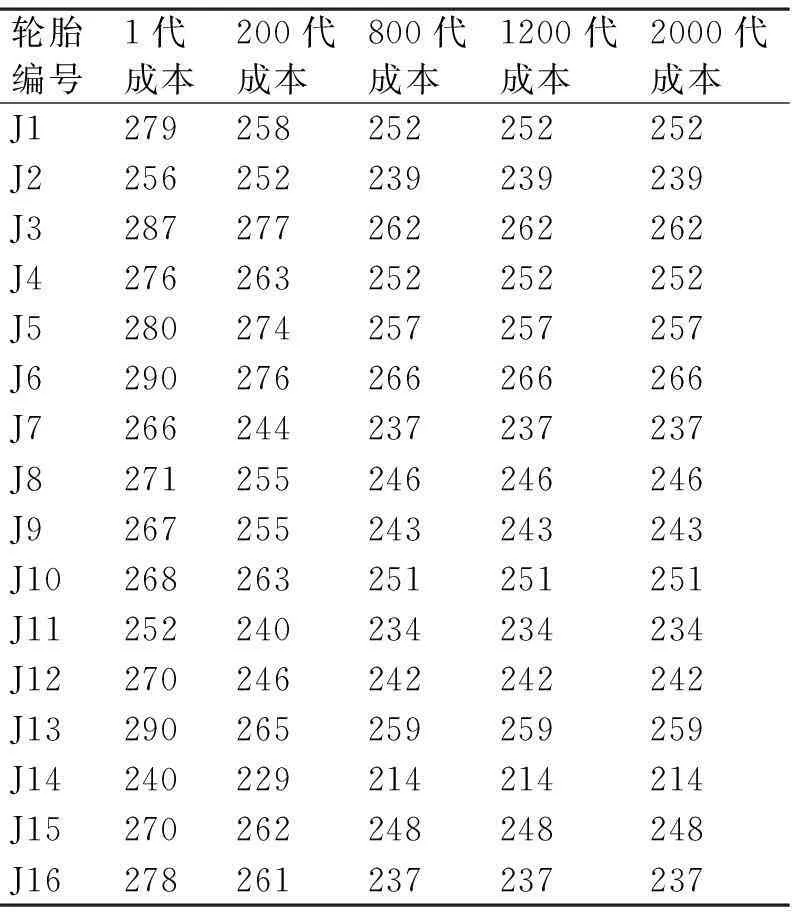
表4　调度结果成本比较

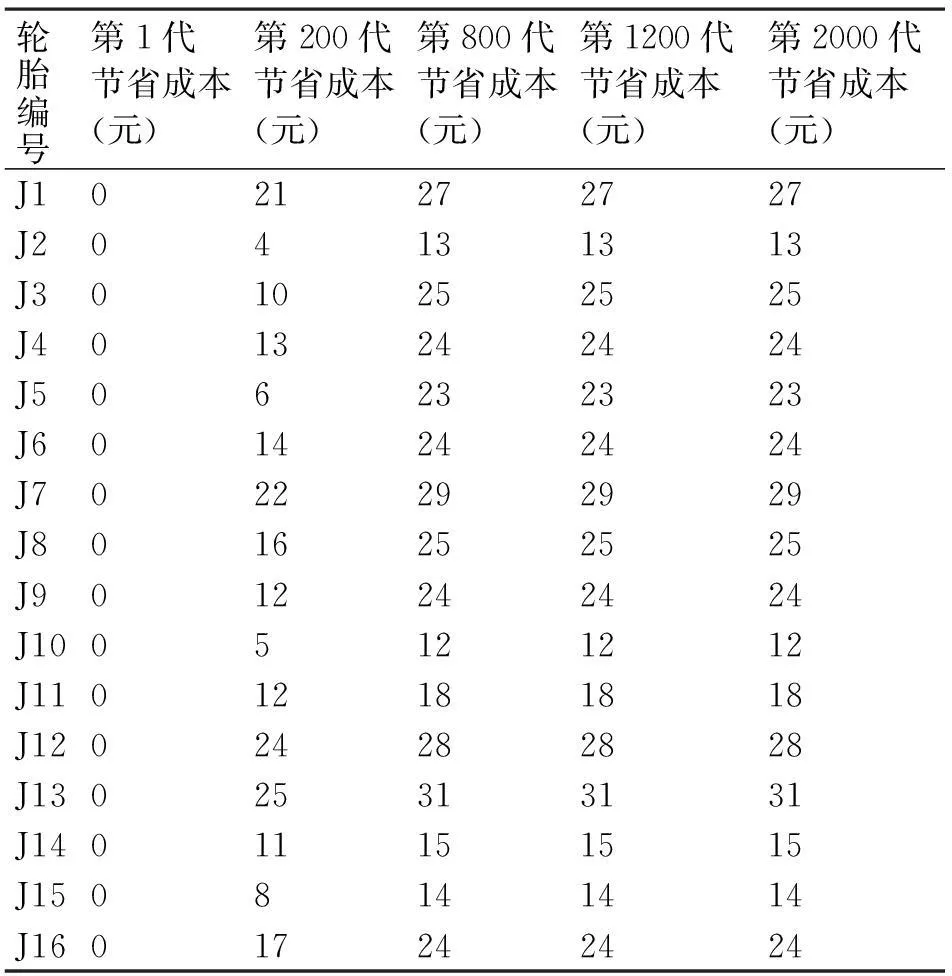
表5　调度结果成本节省

仿真结果表明,在800代时候算法达到稳定的成本节省,以后各代结果与800代的结果相同,表明该算法,每个客户达到成本节省的最大值,结果表明硫化车间调度模型和求解算法的有效性。

4结语

本文结合合作博弈的特点和硫化车间生产调度问题的实际情况,针对客户成本需求问题,建立了基于合作博弈的硫化车间生产调度模型。设计采用遗传算法对模型进行求解,对实验进行仿真后得出的实验结果符合预期结果,以此证明基于合作博弈的硫化车间调度模型是合理、可行的。但是对于合作博弈模型的解的分析和合作联盟成立后的总节省成本的分配等还需进一步研究。

参 考 文 献

[1] 李臣星.基于非合作博弈的多目标硫化车间生产调度研究[D].青岛:青岛科技大学,2013:1-65.

LI Chenxing. Study on vulcanization workshop production scheduling based on non-cooperative game[D]. Qingdao: Qingdao University of Science and Technology,2013:1-65.

[2] 刘丹,陈亮,王伟.一种基于合作博弈的多目标设计问题求解方法[J].机械设计,2014,(8):3.

LIU Dan, CHEN Liang, WANG Wei. Solving methods of multi-objective problems based on cooperative game,2014,(8):3.

[3] 李臣星.客户驱动的硫化车间非合作博弈生产调度研究[J].科技信息,2013,(13):452-452.

LI Chenxing. Study on vulcanization workshop Production Scheduling based on non-cooperative game for customers’ cost demand[J]. Technology Information,2013,(13):452-452.

[4] 周艳平.基于博弈理论的多目标生产调度问题研究[D].上海:华东理工大学,2012:1-78.

ZHOU Yanping. Research of Production Scheduling Problem based on Game theory[D]. Shanghai: East China University of Science and Technology,2012:1-78.

[5] Zhou Yanping, Gu Xingsheng. Research on Flow Shop Scheduling Problem with Multi-customer and Fuzzy Due Date Based on Non-cooperative Games, 2008 IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Proceedings,2008:968-976.

[6] Zhou Yanping, Gu Xingsheng. Research on No-wait Flow Shop Scheduling Problem with Fuzzy Due Date Based on Evolution Games, 2009 2nd IEEE International Conference on Computer Science and Information Technology,2009:490-494.

[7] 王昱文.合作博弈理论的生产调度应用[J].商业经济,2014,(3):21-25.

WANG Yuwen. Application of Cooperative game theory in Production Scheduling[J]. Business Economics,2014,(3):21-25.

[8] 周艳平,顾幸生.一类流水车间调度的合作博弈[J].化工学报,2010,61(8):1983-1987.

ZHOU Yanping, GU Xingsheng. Flow Shop Scheduling based on cooperative game[J]. Chemical Technology,2010,61(8):1983-1987.

[9] Curiel I, Pederzoli G, Tijs S. Sequencing games[J]. European Journal of Operational Research,1989,40(3):344-351.

[10] 郭海东.遗传算法及其在生产调度中的应用研究[D].杭州:浙江工业大学,2004:18-74.

GUO Haidong. Genetic Algorithm and Its Application in Production Scheduling[D]. Hangzhou: Zhejiang University of Technology,2004:18-74.

[11] 李敏强.遗传算法的基本理论与应用[M].第一版.北京:科学出版社,2002:16-69.

LI Minqiang. Basic theory and application of Genetic algorithms[M]. First Edtion. Beijing: Science Press,2002:16-69.

中图分类号TP272

DOI:10.3969/j.issn.1672-9722.2016.02.003

作者简介:胡乃平,男,博士,教授,硕士生导师,研究方向:工业信息化。张立英,女,硕士研究生,研究方向:工业信息化。

基金项目:山东省高等学校科技计划项目(编号:J09LG16,J14LN31);山东省自然科学基金项目(编号:ZR2011FL001)资助。

*收稿日期:2015年8月11日,修回日期:2015年9月26日