基于灰色预测和BP神经网络模型的云南省人口总量预测研究*

何思兰　孙红兵

(昆明理工大学理学院　昆明　650500)



基于灰色预测和BP神经网络模型的云南省人口总量预测研究*

何思兰孙红兵

(昆明理工大学理学院昆明650500)

摘要人口问题一直是关系经济增长和社会稳定的关键问题,因此科学准确的人口预测也越来越重要。论文通过利用历年中国统计年鉴上云南省人口总量数据,分别应用灰色预测和BP神经网络模型对2000~2013年人口总量数据进行仿真模拟,考虑单一预测模型的局限性,然后利用标准差法对单一预测仿真结果进行权重分配,建立了组合预测模型。模型结果表明,组合预测模型优于单一的灰色预测模型和BP神经网络模型,具有较高的精度。最后利用组合预测模型,对2014~2025年的人口总量进行了短期预测,结果表明,到2024年人口总量将突破5000万人,人口增长速度大概维持在0.6%左右。

关键词灰色预测; BP神经网络; 组合预测模型

Population Prediction Research in Yunnan Province Based on Grey Prediction and BP Neural Network

HE SilanSUN Hongbing

(Department of Science, Kunming University of Science and Technology, Kunming650500)

AbstractThe population problem has always been a key issue in the economic growth and social stability, so scientific and accurate forecast of the population is becoming more and more important. In this paper, by using the total population of yunnan province in China statistical yearbook data, simulation the population from 2000 to 2013 by the grey prediction model and BP neural network model, considering the limitations of single forecasting model, then using the method of standard deviation to weight distribution of single forecasting results, that is the combined forecasting model. Model results show that the combined forecasting model is superior to the single grey prediction model and BP neural network model, and it has high precision. Finally the population from 2014 to 2025 is forecasted by combined forecasting model, the results show that the population will exceed 50 million until 2024, and the population growth remain at around 0.6%.

Key Wordsgrey prediction, BP neural network, combination forecasting method

Class NumberC924

1引言

人口数量的多少不仅影响国民经济发展,也影响社会稳定、劳动力就业以及资源的可持续利用等重要因素。在一定程度上科学准确的人口预测,可为政府制定人口有关政策提供理论依据。云南省是西南地区人口大省,也是中国重要的少数民族聚居区,截至2013年总人口数已达到4686.6万人,虽然较2012年人口增长率有所下降,但是人口基数还是较大,人口问题还是面临众多挑战,对于人口的研究有着重要的理论与实际意义。

人口预测是以人口发展规律作为预测主体,将人口分析与预测方法结合运用的过程。近年来,在国内人口预测研究中,不同学者从不同角度对人口问题进行了大量研究。最早的是宋健[1]以控制论为基础,把总和生育率作为控制因子,建立人口控制偏微分方程来预测未来人口趋势[2],但是模型中需要大量的准确数据来确定参数,而这些数据的获取有一定难度;邓聚龙[3~4]建立的灰色预测模型可以在信息量不多的情况下得到较高精度的预测结果,使其应用在人口预测方面也越来越多[5~7];人工神经网络[8~10]由于它的自学习功能以及可以充分逼近任意复杂的非线性关系等优点,近些年来也延伸到了人口预测的运用上。但考虑到单一预测方法的局限性,本文提出了一种基于灰色预测和神经网络预测模型的组合预测模型,充分利用单一预测模型的信息,扬长避短,用以预测云南省短期人口总量变化趋势。

2灰色预测模型

2.1模型介绍

灰色预测模型(GM(1,1))是最常用的对时间序列预测的一种灰色预测模型,模型的实质是对原始序列作一次累加生成,然后建立一阶线性微分方程模型,得到拟合函数以对系统进行预测。其主要过程如下:

1) 累加生成新序列

已知X(0)=(X(0)(1),X(0)(2),…,X(0)(n))为原始数列,其中此文X(0)(·)表示云南省历年人口总数。对原始数据进行一次累加生成,以弱化原始序列的随机性和波动性,得到生成序列:

X(1)=(X(1)(1),X(1)(2),…,X(1)(n))

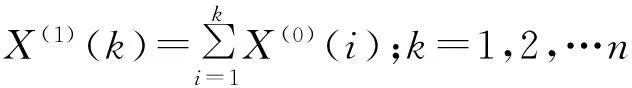
2) 构建GM(1,1)模型

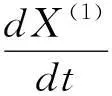
3) 求解a,u

利用最小二乘法,求解a,u为:A=[a,u]T=(BTB)-1BTY,其中

4) 预测结果及还原

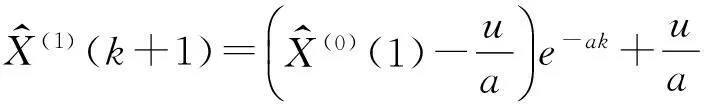
5) 对预测模型进行误差检验。

2.2数值模拟

与传统的预测方法相比,灰色预测方法具有只需少量原始数据便可得到比较精确的结果,通过尝试,本文选取2000~2013年的人口数据进行预测可达较高精度,结果如表1所示。

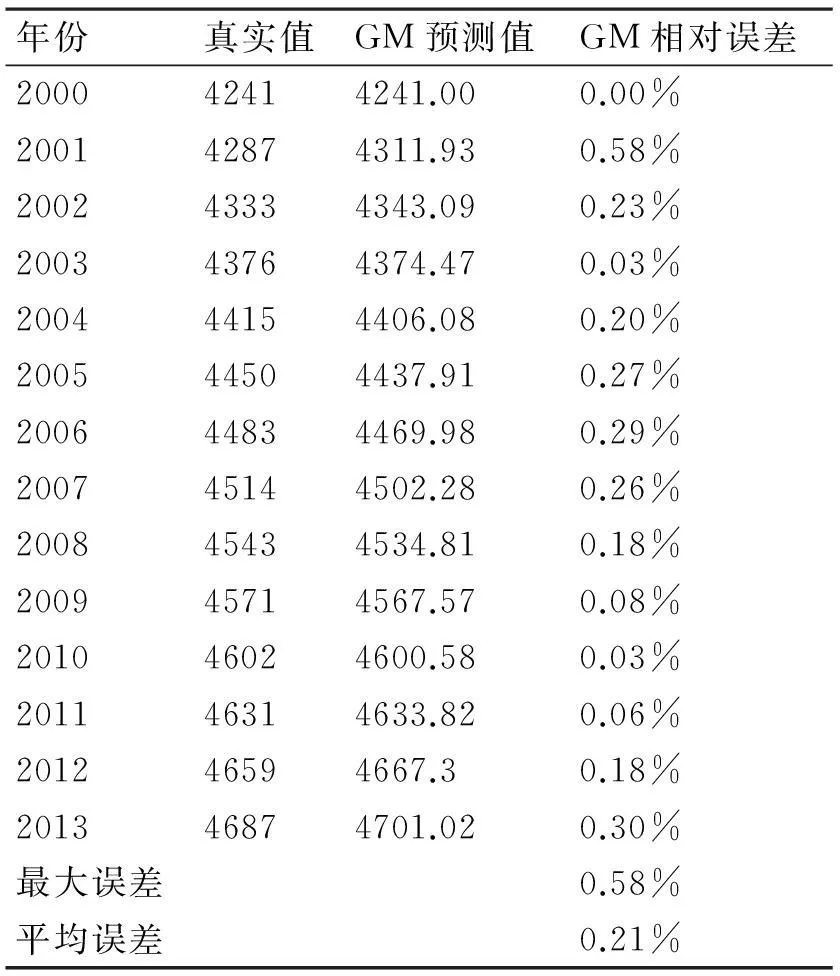
表1　GM(1,1)预测结果

经计算可得,GM(1,1)预测模型为

关联度检验:r=0.625是满足p=0.5时的检验准则r>0.6的;后验差检验:计算方差比c=S1/S0=0.0473,(其中S0,S1分别为原始序列和残差的均方差),并且小残差概率P=1,模拟值精度达到了一级标准,由此可知该模型可用于对云南省短期的人口总量预测。

3BP神经网络模型

3.1模型介绍

BP神经网络是由多个神经元组成的神经网络,它具有记忆、联想、自适应、并行处理和非线性转换等一系列优点。BP神经网络通常是一种三层或三层以上的前向型神经网络,包括输入层、一个或多个隐含层和输出层。其模型结构如图1所示。

BP神经网络模型最大的特点就是在未知因变量和自变量之间的映射关系时,仅仅利用变量和结果可仿真模拟出一个稳定的神经映射。一个完整的BP神经网络由信息的正向传播和误差的反向传播两个过程组成。它的算法是:将输入的数据进行处理,数据经过隐含层处理后由最后一个隐层传递到输出层各神经元,至此完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。在正向学习过程中,输人层、隐含层和输出层面上的各个节点的权重都是随机分配取值。当实际输出与期望输出不符,或者模型精度偏差过大而没有达到预设精度时,处理结果会被保留并进入误差的逆向传播阶段,误差通过输出层按误差梯度下降的方式修正各层权值,向隐层、输入层逐层反传,以使网络的输出不断地接近期望的输出,直到运算结果达到满意精度或者预设学习步数为止。

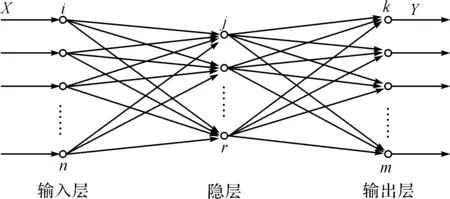
图1　BP神经网络结构

BP模型的算法步骤如下:

1) 初始化全部连接权值w,v及阈值θ,γ赋予(0,1)区间的随机值,设置最大迭代次数和误差限;

2) 对初始数据进行归一化,输入学习样本(P,T);

3) 据各输出单元的输出函数计算各样本模式隐层和输出层各单元的实际输出值;

4) 输出层开始,反方向调整权系数值和神经元阈值;

5) 计算输出层和隐含层的样本误差和总误差;

6) 样本期望输出误差小于给定收敛值,则转至步骤7),否则继续步骤3);

7) 神经网络学习结束。

3.2数值模拟

由于神经网络需要比较多的数据作为训练样本,本文中,我们选取中国人口统计年鉴上1978~2000年云南省人口总量作为训练样本数据,2001~2013年数据作为检验样本数据,采用具有一个隐含层的三层BP神经网络预测系统进行人口预测,通过试算法来确定输入节点和隐含节点,输出结点数取为1。通过试算和仿真,输入节点取8个,隐含节点取10个,选取“tansig”作为输入节点和隐含层节点之间的传输函数,选取“logsig”作为连接隐含层和输出层节点的传输函数,选取“traingdm”为网络的训练函数。结果如表2所示。

表2　BP神经网络预测结果

由以上两种单一预测数据可知,它们的相对误差最大不超过1%,具有较好的精度。灰色预测的最大相对误差0.58%小于BP神经网络的最大相对误差0.66%,平均相对误差0.21%大于BP神经网络的0.19%。并且灰色预测模型只对短期预测精度较好,而不适合中长期预测,而BP神经网络预测没有关于后期的模型检验,可能具有偶然性,为了充分利用单一预测的有效信息,克服单一模型的缺陷,减少预测的随机性,提高预测精度,我们引入组合预测模型。

4人口总量组合预测模型

组合预测方法是由Bates和Granger[11]在1969年提出的一种预测方法,考虑单一预测方法的局限性,综合利用各种预测方法所提供的信息,扬长避短,使其获得更满意的结果,其基本思想是将不同的预测模型和方法结合起来,以适当的方式得出组合预测模型。目前比较常用的组合预测模型有平均值法、递归最小二乘法、模糊逻辑系统、BP神经网络法、标准差法等。考虑到标准差法的简单并且有效等优点,本文应用标准差法,得出最优加权系数作为组合预测模型。

4.1模型介绍

设灰色预测和BP神经网络预测误差的标准差分别为得σ1、σ2,且σ=σ1+σ2,则最优加权系数及组合预测值分别为

其中,ωi为第i种预测方法的加权系数,Xi为第i种预测方法的预测值,Xc为组合预测值。

4.2数值模拟

本例中按照标准差方法计算可得灰色预测模型和BP神经网络模型的权重分别为0.4145,0.5855,则组合预测模型为

Xc=0.4148X1+0.5855X2

结果如表3所示。

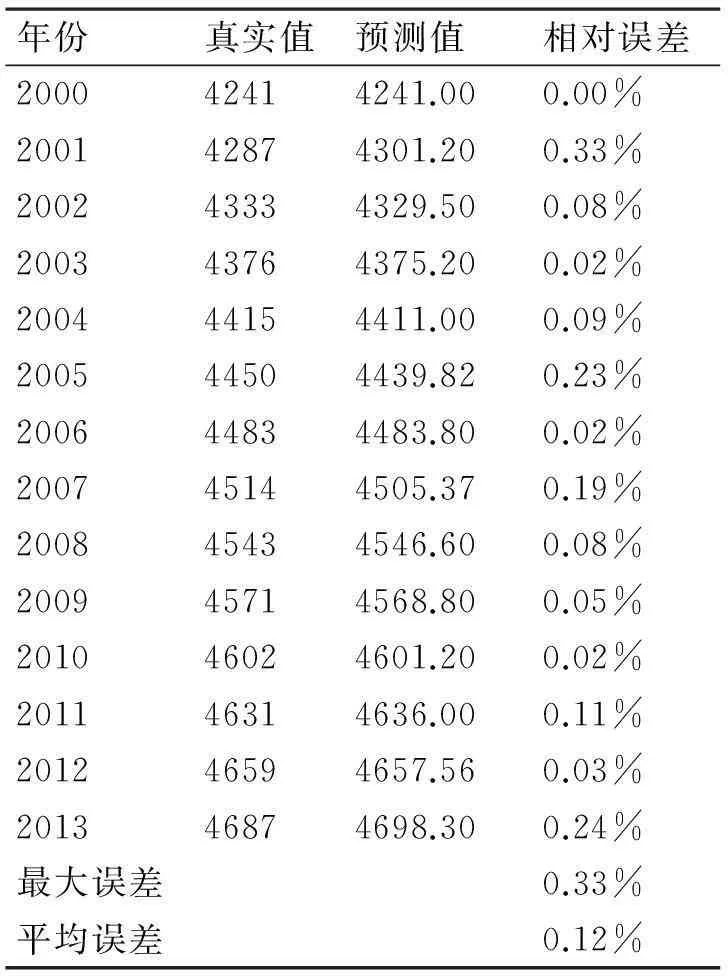
表3　组合模型预测结果

对比表1~表3数据可以看出,该组合预测模型具有很强的预测性,最大相对误差0.33%比任一单一预测模型小,平均误差0.12%也优于单一预测模型,非常适合用于人口预测问题。

4.3实例应用及结果分析

根据上述组合预测模型对云南省2014~2025年的人口总量进行预测。结果如表4所示。

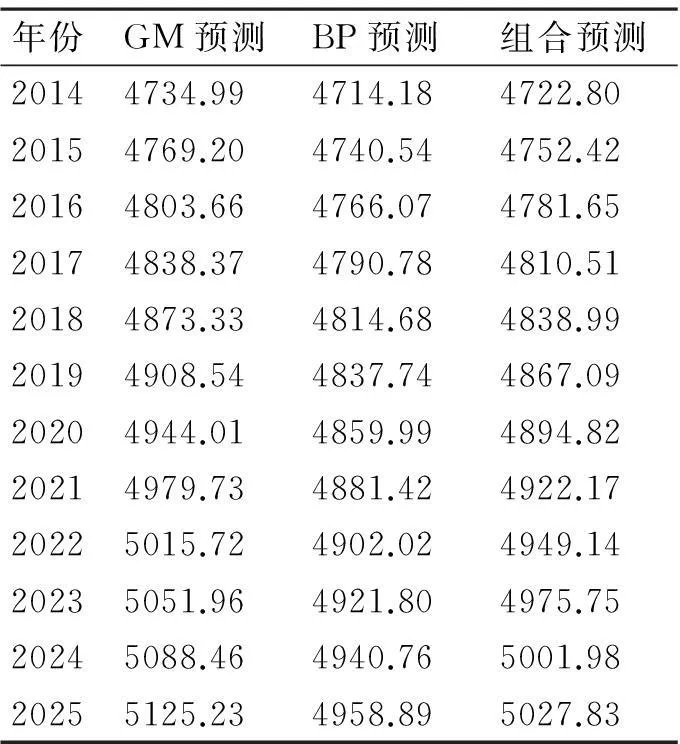
表4　云南省2014~2025预测结果

上述模型对人口总量变化从不同角度进行了模拟、预测及组合。预测结果表明: 1) 从组合预测模型结果来看,在2024年,云南省人口总量将突破5000万人,人口增长速度大概维持在0.6%左右。 2) 任何一种数量模型的预测结果都不可能是完全精确的,这主要是因为任何一种模型都是直接或间接的依据历史数据来建模,而随着时间的推移,与历史数据相联系的内部及外部环境条件会产生各种变化。未来影响人口增减变化的主要因素有:

(1)经济因素。经济因素对人口自然增长的作用主要表现在它决定了人口的增殖条件和生存条件,通过改变人口的出生率和死亡率来影响人口的自然增率。

(2)文化因素。随着科学文学水平的提高,人口自然增长率趋于下降。

(3)医疗卫生因素。医学的进步和医疗卫生事业的发展对人口出生率和死亡率有着直接影响,并且它对控制生育和实行优生优育有着积极的作用。

5结语

本文重点研究了云南省人口总量的短期预测,提出了一种基与灰色预测模型和BP神经网络模型应用标准差法的组合预测模型。应用云南省人口总量对本文提出的组合预测模型方法进行了验证分析,结果表明组合预测模型提高了预测的准确性。

参 考 文 献

[1] 宋健,田雪原,于景元,等.人口预测和人口控制[M].北京:人民出版社,1982:42-75.

SONG Jian, TIAN Xueyuan, YU Jingyuan, et al. Population Forcasting and Population Control[M]. Beijing: People’s Publishing House,1982:42-75.

[2] 宋健,于景元,李广元.人口发展过程的预测[J].中国科学,1980(9):920-933.

SONG Jian, YU Jingyuan, LI Guangyuan. Forecast Population Development Process[J]. Science China Press,1980(9):920-933.

[3] 邓聚龙.灰色系统理论教程[M].武汉:华中科技大学出版社,1990:176-263.

DENG Julong. The Course of Grey System Theory[M]. Wuhan: Huazhong University of Science and Technology Press,1990:176-263.

[4] 邓聚龙.灰色系统基本方法[M].第2版.武汉:华中科技大学出版社,2005:26-73.

DENG Julong. The Primary Methods of Grey System Theory[M]. Second Edition. Wuhan: Huazhong University of Science & Technology Press,2005:26-73.

[5] 王宇熹,汪泓,肖峻.基于灰色GM(1,1)模型的上海城镇养老保险人口分布预测[J].系统工程理论与实践,2010,30(12):2244-2253.

WANG Yuxi, WANG Hong, XIAO Jun. Forecast on Population Distribution of Shanghai Pension System Based on the Gray GM(1,1) Model[J]. Systems Engineering — Theory & Practice,2010,30(12):2244-2253.

[6] 郝永红,王学萌.灰色动态模型及其在人口预测中的应用[J].数学的实践与认识,2002,32(5):813-820.

HAO Yonghong, WANG Xuemeng. The Dynamic Model of Gray System and Its Application to Population Forcasting[J]. Mathematics in Practice and Theory,2002,32(5):813-820.

[7] 陈楠,林宗坚,王钦敏,等.基于灰色理论的中国人口空间分布模式预测[J].经济地理,2006,26(5):759-762.

CHEN Nan, LIN Zongjian, WANG Qinmin, et al. The Forecast on the Population Spatial Distribustion Pattern Based on the Gray Theory[J]. Economic Geography,2006,26(5):759-762.

[8] 罗荣桂,黄敏镁.基于BP神经网络的长江流域人口预测研究[J].武汉理工大学学报,2004,26(10):90-93.

LUO Ronggui, HUANG Minmei. Study on Population Prediction of Yangtze Basin Based on BP Neural Network[J]. Journal of Wuhan University of Technology,2004,26(10):90-93.

[9] 尹春华,陈雷.基于BP神经网络人口预测模型的研究与应用[J].人口学刊,2005(2):44-48.

YIN Chunhua, CHEN Lei. The Research and Application of Population Prediction Based on BP Neural Network Model[J]. Population Journal,2005(2):44-48.

[10] 赖红松,祝国瑞,董品杰.基于灰色预测和神经网络的人口预测[J].经济地理,2004,24(2):197-201.

LAI Hongsong, ZHU Guorui, DONG Pinjie. Population Forecast Based on Combination of Gray Forecast and Artificial Neural Networks[J]. Economic Geography,2004,24(2):197-201.

[11] Bates J M, Granger C W. Combination of Forecasts[J]. OperationaI Res Ouart,1969,20(4):451-468.

中图分类号C924

DOI:10.3969/j.issn.1672-9722.2016.02.001

作者简介:何思兰,女,硕士研究生,研究方向:人口经济等。孙红兵,女,博士,教授,硕士生导师,研究方向:创新管理和区域经济等。

基金项目:国家自然科学基金“创新型企业持续创新机遇的决策模式与机制研究”(编号:71262016);国家自然科学基金“节能减排进程中高耗能产业群循环经济协同效应与协调优化研究”(编号:71463031)资助。

*收稿日期:2015年6月12日,修回日期:2015年9月24日