低空目标被动声定位误差仿真*

雷　斌　侯添译

(西安工业大学电子信息工程学院　西安　710021)



低空目标被动声定位误差仿真*

雷斌侯添译

(西安工业大学电子信息工程学院西安710021)

摘要针对低空目标声场特性,在到达时延(Time Delay of Arrival,TDOA)定位算法基础上,建立一种针对低空目标定位误差的数学模型GDOP(Geometric Dilution Precision)。对常用的布站方式进行定位误差仿真分析,从仿真结果中可以得出最优布站方式,此数学模型可作为衡量低空目标定位最优布站方式之一。

关键词低空目标; 到达时延; 布站方式; 定位精度因子

Low-altitude Target Passive Localization Error Simulation

LEI BinHOU Tianyi

(School of Electronic and Information Engineering, Xi’an Technological University, Xi’an710021)

AbstractAiming at low-altitude targets feature, a mathematical model GDOP(Geometric Dilution Precision) is established based on the TDOA(Time Delay of Arrival). The error simulation is used for analyzing commonly used station placement in the model and then finds the best pattern of station placement. So the mathematical model can be used as one of the best way to measure low-altitude target location station placement.

Key Wordslow-altitude target, TDOA, station placement, GDOP

Class NumberTN911

1引言

近年来,雷达探测面临低空目标突袭、隐身技术和电磁干扰技术的威胁,而现有常规性雷达针对低空目标的探测,有着其不足之处:从低空障碍物反射回来的杂波有着极强的干扰性,有用的目标回波信号难免会被完全淹没,受地形的干扰,低空障碍物反射杂波的干扰会产生低仰角盲区,无法识别低空目标[1~5,10]。然而现有针对低空目标声定位,一般采用声传感器测距定位,但是其容易受到定位系统设备和外界环境干扰因素的影响。所以通过针对性的定位算法,减小误差。常用的针对低空目标定位算法可以根据不同测量值分为:到达时间(Time of Arrival,TOA)、定位到达角(Angle of Arrival,AOA)、到达时延(Time Difference of Arrival,TDOA)[7]。本文简述基于TDOA的低空目标定位算法,提出一种定位精度因子的(Geometric Dilution Precision,GDOP)的数学模型,对常见的四元声阵列布站进行定位误差仿真,作为衡量低空目标定位最优布站方式之一。

2TDOA定位算法

针对低空目标被动声定位问题,到达时间算法对时间同步要求较高,定位到达角算法易受外界环境干扰,必须添加去噪声硬件,导致成本增加,而到达时延算法对时间基准的依赖性较低,特别是针对单个声源定位误差较小。到达时延算法通过估计待测低空目标的声信号与到达阵列中各节点的相对时延,从而可以计算出低空目标信号到达各节点的距离差,采用几何算法或者搜素算法来确定出待测低空目标位置[9]。

假定目标信号为S(t),在一定的区域内布设N个声传感器构成传感器阵列,第i个节点所接收到的声信号数学模型为

Zi(t)=AiS(t-τi)+ωi(t)

(1)

其中i=1,2,…,n,Ai是第i个节点所接收到信号幅值,τi为低空目标声信号到第i个节点的时间延迟,ωi是外界噪声干扰[6]。

将第1节点作为参考节点,其他节点相对于参考节点可以表示为

Z2(t)=A2S(t-τ21)+ω1(t)

Z3(t)=A3S(t-τ31)+ω2(t)

…

Zn-1(t)=An-1S(t-τn1-1)+ωn-1(t)

Zn(t)=AnS(t-τn1)+ωn(t)

(2)

式中τi1表示低空目标声信号到声传感器阵列节点i与参考节点“1”之间时间差。

3定位精度因子(GDOP)数学模型

GDOP值是指通过站址误差与时间延迟误差值来反映定位误差大小[8]。在低空目标定位系统中,该值与定位误差值呈反比例关系。本文建立一种定位精度因子数学模型对常见的四元声传感器阵列进行定位误差分析。

在TDOA算法中,通过求解由N个相对时延方程可得:

ΔZi=Zi-Z0≈c·(τi1+δt)

(3)

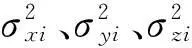
d(ΔZi)=(Gix-G0x)dx+(Giy-G0y)dy

+(Giz-G0z)dz+(ki-k0)

(i=1,2,…,n)

(4)

(5)

由上述公式可知,可得三个方向上定位精度的方差及GDOP值为

(6)

(7)

4仿真分析

在该算法可实现前提下,对常见的四元声阵列布站,如四元星形布站、四元菱形布站进行定位精度因子仿真分析。如图所示,图中曲线上数字反映的是不同布站方式下的定位误差,曲线组则是对应条件下的等距离误差曲线,仿真环境:Matlab R2013a。

仿真条件A:假设被定位的低空目标在理想条件下,低空目标坐标为(300,300,300),四元声传感器各节点间距200m,时间延迟误差为0.003s,声传感器节点距离误差为5cm,两种布站在不同时间延迟下的定位精度因子分布如图1~4所示。

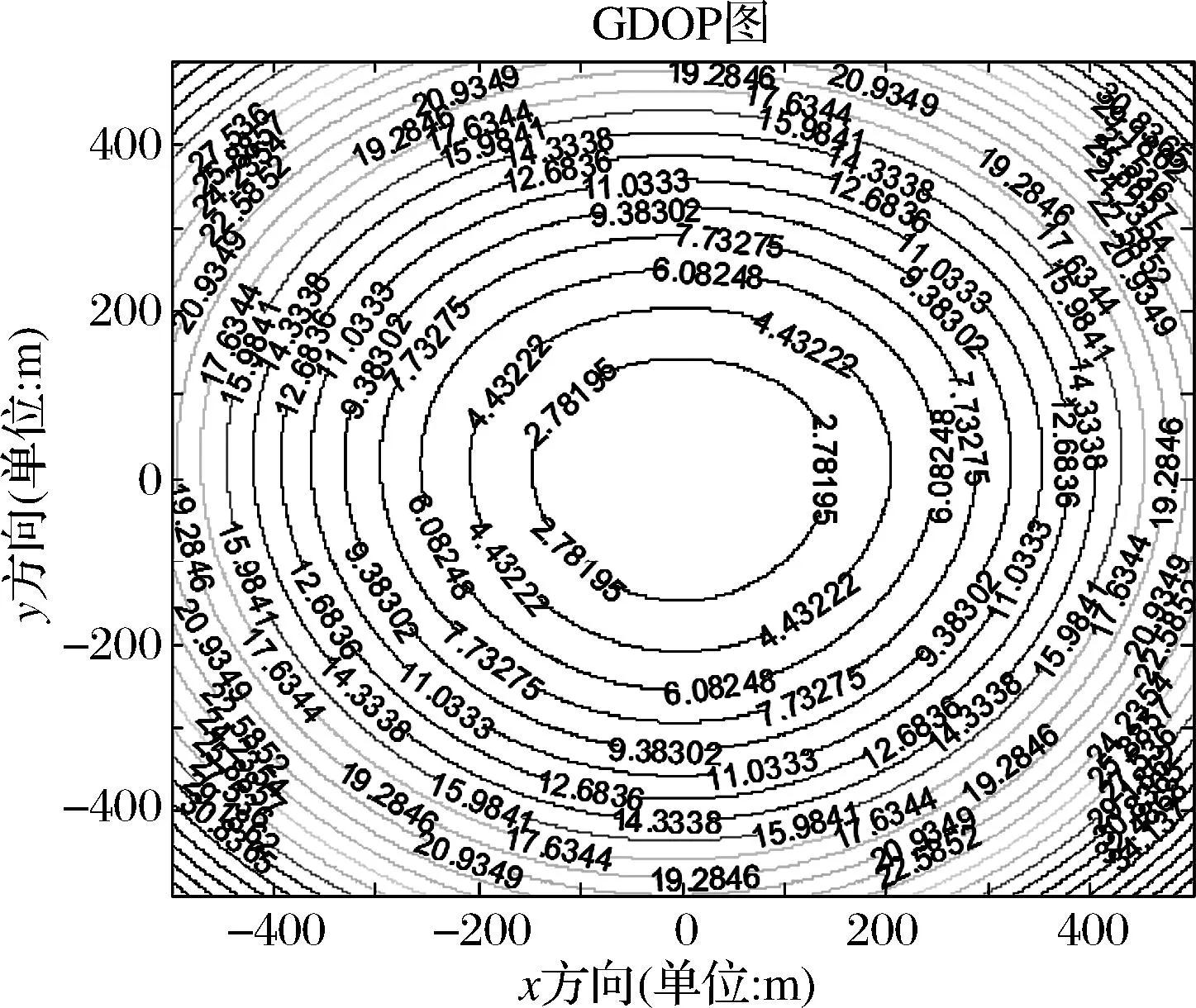
图1　四元星型:时延0.003s,定位精度2.78195m

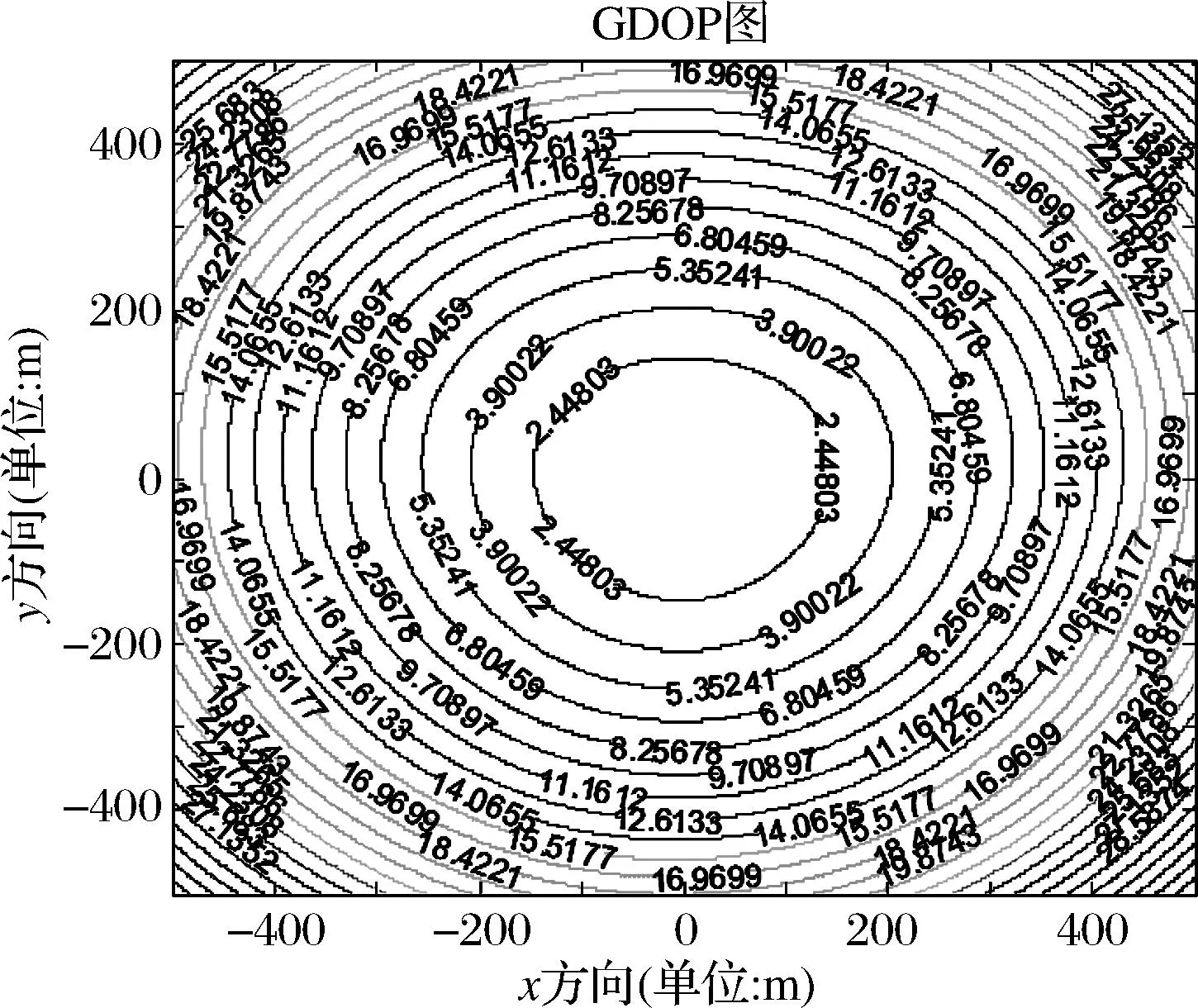
图2　四元星型:时延0.002s,定位精度2.44803m

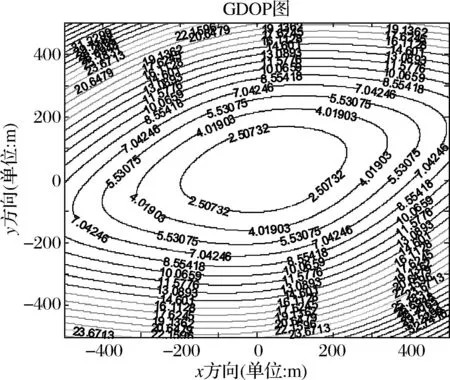
图3　四元菱形:时延0.003s,定位精度2.50732m

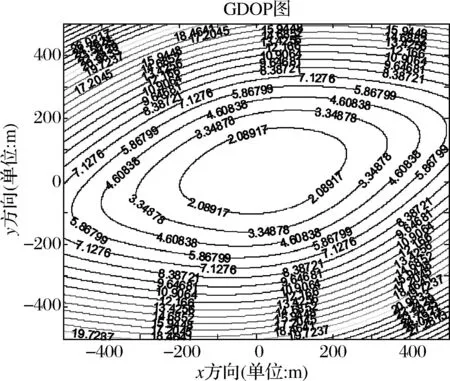
图4　四元菱形:时延0.002s,定位精度2.08917m

由图1~4可知,在时间延迟误差,声传感器节点间距误差等因素相同的条件下,时间延迟越小,定位精度越高,在声传感器节点间距、时间延时相同的条件下,四元菱形基站布阵,定位误差较小。

仿真条件B:假设被定位低空目标处于理想条件下,低空目标坐标为(300,300,300),四元声传感器各节点间距200m,时延估计误差为0.003s,两种布站方式在不同节点间距误差下的定位精度因子分布如图5~8所示。

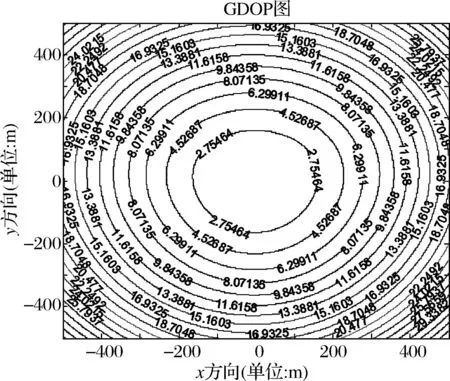
图5　四元星型:节点间距误差4cm,定位精度2.75464m

由图5~8可得,在相同的布站方式下,声传感器节点间距误差的减小,定位误差减小。在相同的节点间距误差条件下,四元菱形定位误差小于四元星型。

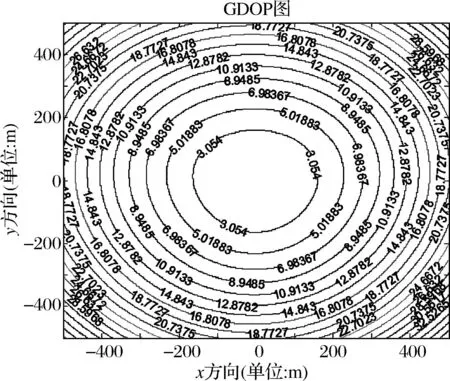
图6　四元星型:节点间距误差8cm,定位精度3.054m

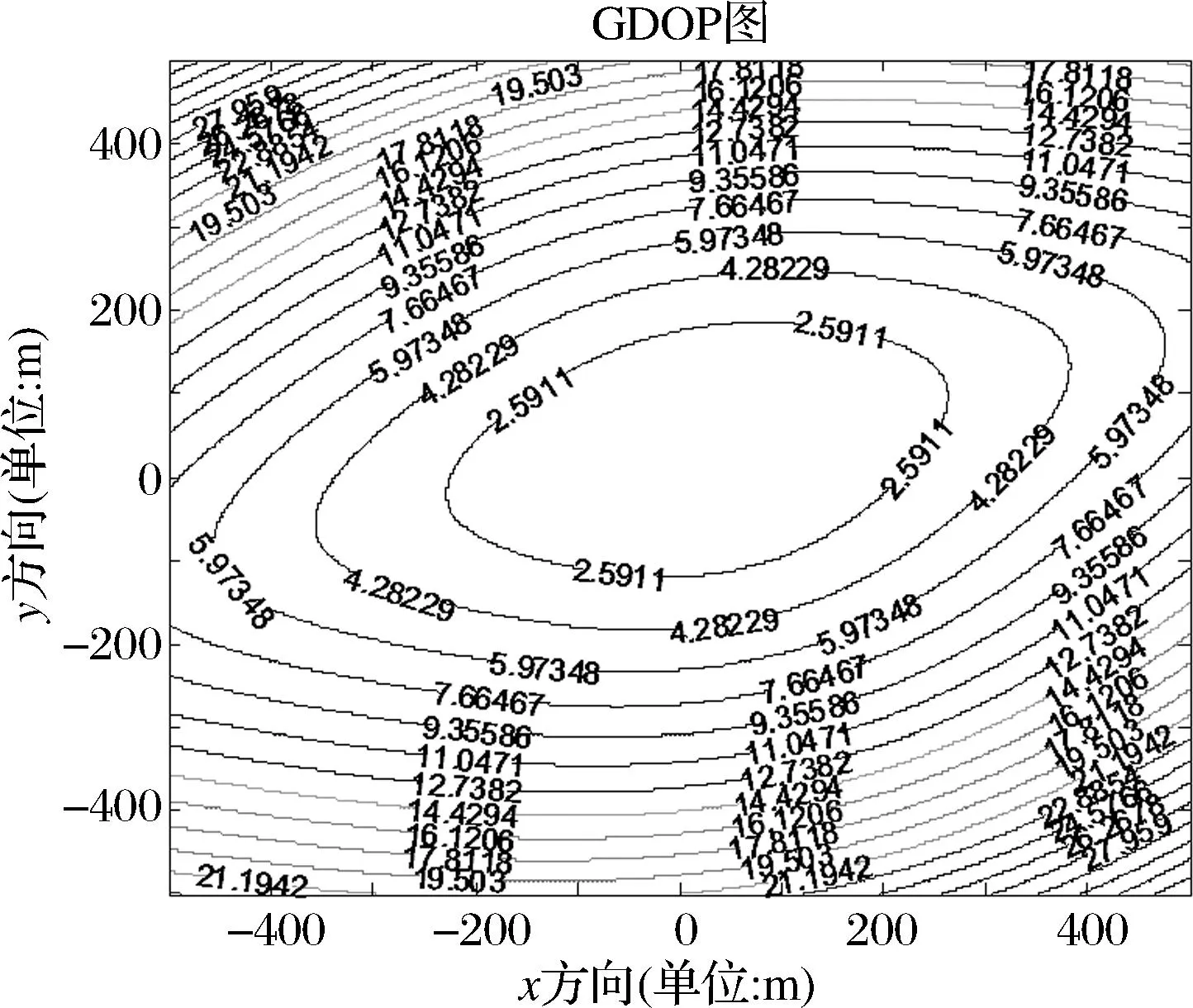
图7　四元菱形:节点间距误差4cm,定位精度2.5911m

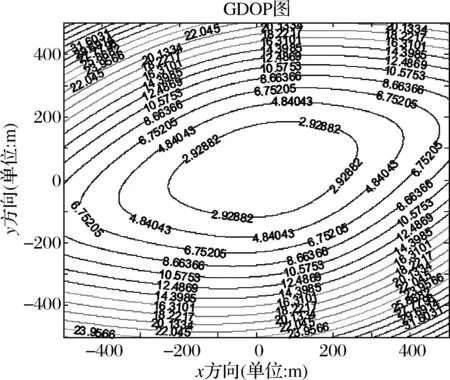
图8　四元菱形:节点间距误差8cm,定位误差2.92882m

5结语

本文针对低空目标定位的到达时延算法进行研究,针对不同的布站方式、时延、节点间距误差等进行定位精度因子误差仿真。由以上仿真可以看出,四元菱形布站,定位误差小于四元星型布站。因此,在选择最优低空目标定位布站方式时,该模型不失为一种很好的衡量方式。

参 考 文 献

[1] Steven M K.统计信号处理基础—信号估值与检测理论[M].罗鹏飞,张文明,刘忠,译.北京:电子工业出版社,2006:100-150

Steven M K. Basis of Statistical Signal Processing-Signal Estimation and Detection Theory[M]. LUO Pengfei, ZHANG Wenming, LIU Zhong, Translated. Beijing: Electronic Industry Press,2006:100-150.

[2] 周泽均,欧阳清,陈遥沛.关于声源阵列2种排列方式的比较[J].舰船科学技术,2014,36(7):91-92.

ZHOU Zejun, OU Yangqing, CHEN Yaopei. Compartments about quality of two ways of sources arrayed[J]. Ship Science And Technology,2014,36(7):91-92.

[3] 孙舟.分布式声源定位关键参数设计及定位算法实现[D].西安工业大学硕士学位论文,2011:5-20.

SUN Zhou. Key Parameters Setting and Location Algorithm for a Distributed Sound Source Positioning System[D]. Master Thesis. Xi’an Technological University,2011:5-20.

[4] 雷斌,孙舟.分布式声源定位算法实现[J].西安工业大学学报,2011,31(2):170-172.

LEI Bin, SUN Zhou. Distributed Source Localication Algorithm[J]. Journal of Xi’an Technological University,2011,31(2):170-172.

[5] 崔玮玮,曹志刚,魏建强.声源定位中的时延估计技术[J].数据采集与处理,2007,22(1):90-99.

GUI Weiwei, CAO Zhigang, WEI Jianqiang. Time Delay Estimation Techniques in Source Location[J]. Journal of Data Acquisition & Processing,2007,22(1):90-99.

[6] 王巍,薛安克,林岳松.无源单传感器声目标纯方位定位改进算法[J].杭州电子科技大学学报,2005,25(3):71-73.

WANG Wei, XUE Anke, LIN Yuesong. An Improved Algorithm of Passive Bearings-only Localization in Single Sensor Acoustic Target[J]. Jounal of Hangzhou Dianzi University,2005,25(3):71-73.

[7] Lin Zhibin, Xu Boling. Three-dimensional Localization of Multiple Acoustic Sources Using Spherical Microphone Array[J]. Nanjing University(Natural Sciences),2007,4(20):374-394.

[8] 贾云得,冷树林,刘万春.四元被动声定位敏感传感阵列定位模型分析和仿真[J].兵工学报,2001,22(2):206-209.

JIA Yunde, LENG Shulin, LIU Wanchu. Modeling of passive acoustic sensing with four-sensor array for target localization[J]. Acta Armamenterii,2001,22(2):206-209.

[9] Nardone S C, Aidala V J. Observability criteria for bearing-only target motion analysis[J]. IEEE Transactions on Aerospace and Electronic Systems,1992,28(4):1077-1085.

[10] 苗晟,周维,唐浩.一种声源定位系统设计[J].计算机科学,2013,40(11A):398-400.

MIAO Sheng, ZHOU Wei, TANG Hao. Acoustic Location System Design[J]. Computer Science,2013,40(11A):398-400.

中图分类号TN911

DOI:10.3969/j.issn.1672-9722.2016.02.012

作者简介:雷斌,男,硕士,副教授,研究方向:测控系统,无线传感器网络、嵌入式系统等。侯添译,男,硕士研究生,研究方向:多传感器信息融合与控制。

*收稿日期:2015年8月12日,修回日期:2015年9月22日