小波多尺度分析的浸润线预测方法
2016-03-15邱坤南沈斐敏
邱坤南, 沈斐敏
(福州大学土木工程学院, 福建 福州 350116)
小波多尺度分析的浸润线预测方法
邱坤南, 沈斐敏
(福州大学土木工程学院, 福建 福州 350116)
为提高浸润线的预测精度, 减少尾矿库安全预警的误报和漏报, 采用小波多尺度分析方法对浸润线监测数据序列进行预处理, 并利用Matlab程序实现. 以MAE, MSE, MAPE, MSPE作为预测精度的评价指标, 对两个工程实例进行研究. 结果表明: 多尺度小波分析预测模型的MAE, MSE, MAPE, MSPE值较其他模型低. 因此, 通过多尺度小波分析处理, 能够较大地提高预测模型的预测精度.
浸润线; 小波多尺度分析; 非平稳时间序列; 尾矿库; 预测
0 引言
浸润线是影响尾矿库安全的众多因素中最为重要的, 有学者称其为尾矿坝的生命线. 通过分析尾矿坝溃坝调查数据, 浸润线过高是溃坝的征兆之一. 尾矿坝浸润线是一个复杂系统, 其影响因素有很多, 如尾矿库内库水、 大气降雨等. 另外, 据相关研究分析, 浸润线位置每降2 m, 库坝体静力稳定性安全系数就增0.1, 甚至更多[1-3]. 因此, 掌握浸润线变化规律并精确预测其位置以及发展趋势, 有利于准确评判尾矿库安全度.
浸润线预测是在监测数据的基础上, 通过运用相关的数理方法、 技术, 合理地预判浸润线位置情况. 浸润线的监测数据序列一般具有周期性、 非平稳趋势性及多尺度特征, 很多预测模型法对这类监测序列进行建模、 预测时存有不足, 预测难度越来越大, 精度也不高. 目前, 浸润线预测的主要方法有: 灰色模型GM(1, 1)[4]、 支持向量机模型(SVM)[5]、 时间序列模型和神经网络模型等[6]. 灰色GM(1, 1)模型的主要特点是所用数据量较少且预测较为准确, 然而由于它的形状简单, 是特定的指数曲线, 在处理波动范围较大的数据时, 该模型的预测难度增大, 预测精度也较低. SVM参数的选择决定了其学习性能和泛化能力, 其在具体应用过程中存在着一个突出的问题, 即如何选择影响算法性能的关键参数, 目前一般都通过梯度下降法算法、 遗传算法和粒子群算法等, 但这些算法都有各自的缺陷. 如用梯度下降法确定, 不仅效率较低, 且稳定性不高. 神经网络具有自学习与高速寻找优化解的能力, 但是在面对变化与波形起伏较大的数据时, 很难收敛, 预测效果不好, 预测精度也不高[7]. 小波多尺度分析由于其独特的分析能力成为提取这类序列变化特征的有力工具, 它最大的优点是能将时间序列按不同尺度分解成具有不同尺度分辨率的高频、 低频信号, 所得信号的平稳性比原信号有明显提高, 使问题简单化, 便于分析和预测[8].
因此, 结合两个工程实例, 对尾矿库的浸润线监测数据进行小波多尺度分析预处理, 建立预测模型, 并将预测结果与未进行多尺度分析预处理的预测结果相比较分析, 证明前者能够有效提高浸润线的预测精度.
1 浸润线数据多尺度分析
根据浸润线监测数据序列特征, 采用离散小波变换对数据进行处理, 对原始信号s进行不同尺度上的分解. 这过程相当于采用高通、 低通两个滤波器, 分别对监测信号进行滤波[9]. 高通滤波器将监测信号的高频成分d滤出, 低通滤波器将信号的低频成分a滤出. 分解过程如图1所示[10]. 对于图1, 存在如下关系:
(1)
通常用Mallat算法实现多尺度的小波分解和重构[11], 则Mallat算法的分解式为:
(2)
式中:H、G分别表示低通、 高通滤波器.
利用式(2)可以把s分解为d1,d2, …,dj和aj(j为分解层数),dj、aj分别称为原始信号在分辨率为2-j的高频(细节)信号和低频(逼近)信号.
为保证预测的可靠性, 通过Mallat算法对分解后的高频、 低频信号进行重构, 公式如下:
(3)
式中G*、H*分别是G、H的对偶算子. 小波分解后的信号通过式(3)进行重构, 且存在:
(4)
式中:Aj为第j层低频信号的重构结果;D1,D2, …,Dj分别为第1至j层高频信号的重构结果.
2 基于多尺度分析的模型建立
设X={x1,x2, …,xn}为浸润线监测系统采集
到的原始序列, 利用多尺度小波对其分解, 再通过式(3)对分解后的信号进行重构, 而后分别对每层高频信号Dk: {Dk, 1,Dk, 2, …,Dk, n}(k=1, 2, …,j)以及低频信号Ak: {Ak, 1,Ak, 2, …,Ak, n}进行建模及检验, 建立共j+1个预测模型; 对每个Dk(k=1, 2, …,j)和Ak进行预测, 得到最终预测值:
(5)
多尺度分析的浸润线预测模型建立的具体流程如图2所示.
按照预测效果评价原则, 选用平均绝对误差(MAE)、 均方误差(MSE)、 平均绝对百分比误差(MAPE)、 均方百分比误差(MSPE)作为预测的精度评价指标[12].
3 工程实例分析
3.1 工程概况
工程实例一: 攀枝花某尾矿库, 采用上游法堆坝, 属于二等库. 选取该尾矿库尾矿坝J-J剖面的3号监测孔, 于1984-01至2000-12期间共204个监测数据作为原始数据序列, 具体如表1所示.
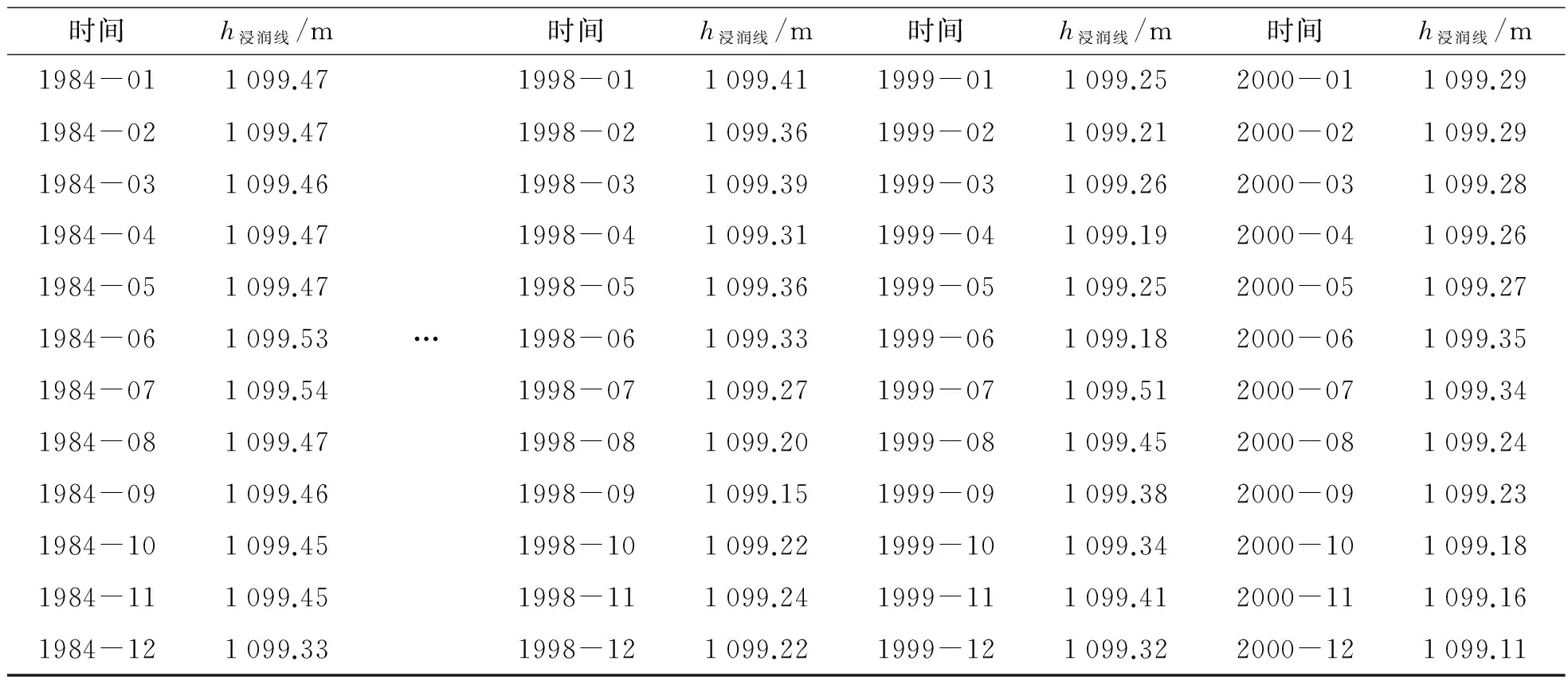
表1 攀枝花某尾矿库J-J剖面3号监测孔原始监测数据Tab.1 The original monitoring data of the No. 3 monitoring hole on a tailings’ J-J profile in Panzhihua
工程实例二: 天宝集团福建某尾矿库, 采用上游式筑坝, 属于三等库. 选取该尾矿库尾矿坝8.89 m处的2号浸润线传感器, 于2014-08至2014-09期间共32个监测数据作为原始数据序列, 如表2所示.
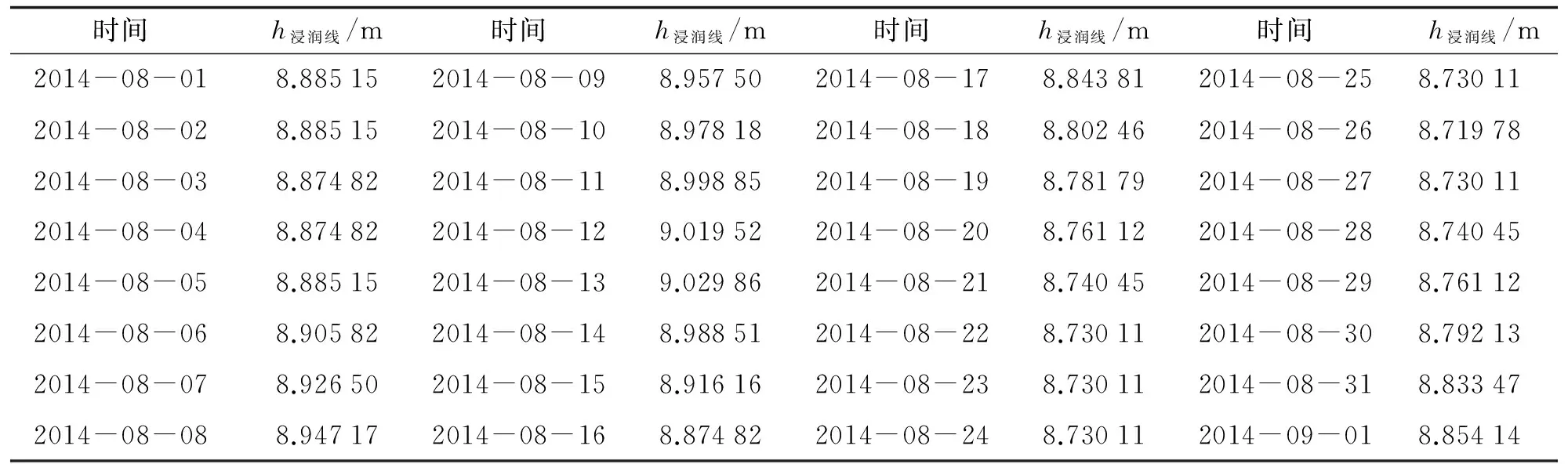
表2 福建某尾矿库尾矿坝8.89 m处2号浸润线传感器原始监测数据Tab.2 The original monitoring data of the No. 2 monitoring hole on the 8.89 m dam of a tailing in Fujian
3.2 建立预测模型
选取实例一的前168个数据用于预测模型的建立, 后36个数据用于预测结果的比较性验证. 同样地, 选取实例二前22个数据用于预测模型的建立, 后10个数据用于预测结果的比较性验证.
对于数据序列的多尺度分析处理, 选取db3基小波函数. 而分解层数应选择合适的尺度, 既可以进一步分解没有细分的高频部分, 又不会使高频部分过于突出[13]. 取j=3, 借助Matlab软件处理数据. 图3、 图4分别是两个尾矿库分解后不同尺度上信号的重构结果.
小波分析的主要Matlab代码如下:

[C,L]=wavedec(s,3,'db3');%多尺度分解cA3=appcoef(C,L,'db3',3);%提取低频信号cD2=detcoef(C,L,'db3',2);%L为记录向量A3=wrcoef('a',C,L,'db3',3);%重构低频信号D2=wrcoef('d',C,L,'db3',2)cD1=detcoef(C,L,'db3',1);%提取高频信号cD3=detcoef(C,L,'db3',3)D1=wrcoef('d',C,L,'db3',1);%C为小波解向量D3=wrcoef('d',C,L,'db3',3)
3.2.1 自回归模型和基于多尺度分析的自回归模型
1) 构建自回归模型. 设时间序列为{xt/t=1, 2, …,N}, 则其自回归模型表示为:
(6)
式中:φ1,φ2, …,φn为自回归模型参数;n为模型阶数;at满足独立正态分布, 其中均值为零, 方差为σ2.
两尾矿库的自回归模型预测结果如图5所示. 其中, 阶数n的确定及参数φ的估计是建立自回归模型最为关键的内容. 可借助AIC准则来确定n, 再通过参数最小二乘法及Ipc全极点模型的自互相关法对φ进行估计, 再通过检验{at}是否为白噪声来检验模型的适用性[13-15]. 经过对模型的阶数n的确定、 参数φ的估计以及适用性检验后, 即可建立自回归预测模型. 最终确定攀枝花某尾矿库与福建某尾矿库的自回归模型阶数n分别为10和2.
2)构建多尺度分析自回归模型. 先对原始数据进行多尺度分析, 分解为低频信号A3和高频信号D1、 D2、 D3, 然后再对其进行自回归建模. 攀枝花某尾矿库与福建某尾矿库的自回归模型阶数n分别为: 10、 8、 10、 8和1、 6、 4、 4. 最终预测结果如图5所示. 以上过程均借助Matlab软件实现, 由于篇幅限制, 这里未将Matlab代码附上.
3.2.2 神经网络模型和基于多尺度分析的神经网络模型
1)构建神经网络模型. 将月份作为输入因子, 实际监测值作为输出因子, 进而确定了该模型的输入节点数为1, 输出节点数为1. 选用Logsig-Purelin函数为模型的激活函数, 而训练函数则采用Traingdx函数. 网络进行训练时, 学习速率选为0.01, 训练次数上限为10 000次, 训练精度要求为0.001.
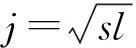
结合前述观点, 对不同的j进行模拟训练, 将能够满足网络要求的收敛速度及训练精度, 并且效果最好的结构作为最终的模型结构[18]. 利用Matlab编制程序实现以上步骤, 下面以福建某尾矿库为例, 不同隐含层神经元网络训练结果示意图如图6所示(这里只选择4个不同的隐含层数进行示意). 以上4个训练结果的均方误差(MSE)分别为0.027 4、 0.018 9、 0.025 7、 0.021 9. 相比较后, 隐含层为6的预测精度相对较好, 因此最终确定神经网络结构. 根据以上方法对两个尾矿库进行神经网络预测, 其中模型的隐含层数分别为16和6, 其预测结果如图7所示.
2)构建多尺度分析神经网络模型. 首先对原始数据进行多尺度分析, 分解为低频信号A3和高频信号D1、 D2、 D3, 然后再对其进行神经网络建模. 攀枝花某尾矿库与福建某尾矿库的神经网络模型中隐含层数分别为: 5、 3、 4、 3和27、 13、 3、 4. 最终预测结果如图7所示.
4 结果分析及讨论
利用前文所构建的模型, 计算所得结果如表3所示.
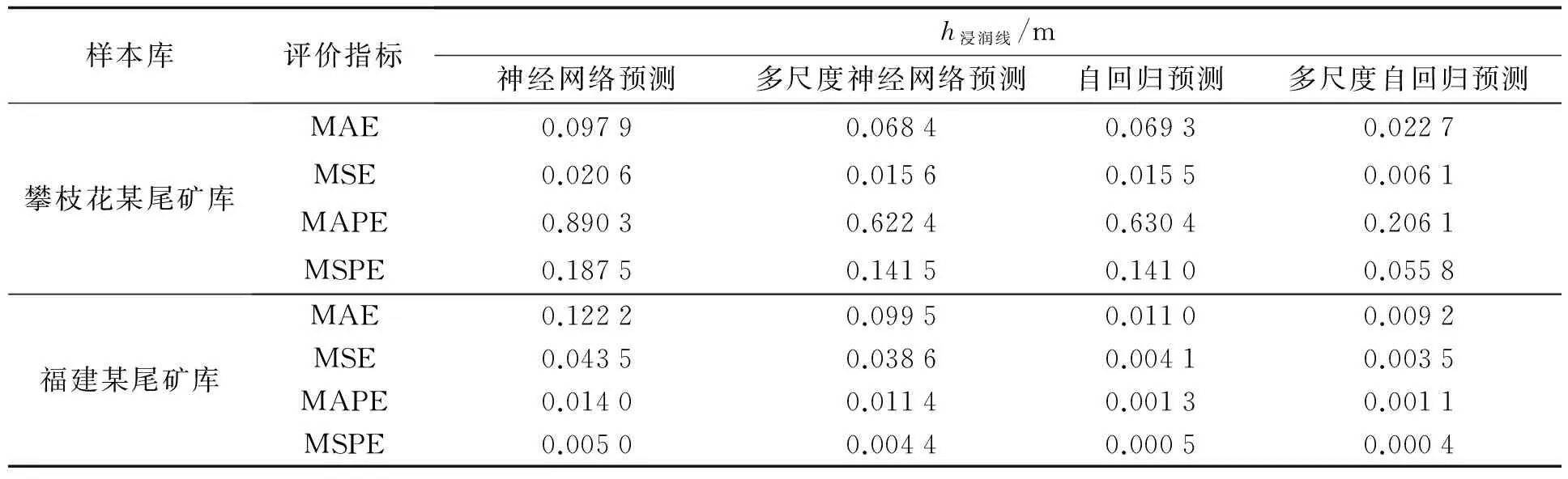
表3 预测结果评价Tab.3 Predicted results evaluation
由图5、 图7和表3可知:
1) 基于多尺度的自回归预测模型、 神经网络预测模型的预测精度较未采用的明显提高, 即对于非平稳数据序列, 采用多尺度分析法进行处理的效果会更加显著, 证明将多尺度分析应用与非平稳数据序列的预测是可行的.
2) 基于多尺度自回归预测模型的预测精度较其他三种预测效果好. 神经网络模型预测的效果最差, 特别是福建某尾矿的预测误差最大, 平均误差达到0.12 m, 可能由于训练样本的数量过于少导致.
3) 多尺度分析法均可通过Matlab软件编程实现, 只是基于多尺度的自回归预测模型、 神经网络预测模型较未采用的多一个步骤, 即先对数据进行多尺度分析, 然后再采用神经网络或自由回归进行预测.
5 结语
1) 利用小波多尺度分析理论, 将非平稳的数据序列转化为近似意义上的平稳信号, 结合自回归模型和神经网络模型进行预测, 通过预测结果与自回归、 神经网络的相比, 基于多尺度小波分析的预测模型预测精度更高, 达到了很多的逼近效果, 验证了该方法的正确性和实用性.
2) 所提方法为尾矿库浸润线预测提供一种新的思路和途径.
3) 通过小波多尺度分析, 将原始序列分解成高频和低频信号, 结合其他预测模型进行建模, 最终得到预测结果. 由于不同尺度上预测的精度不同, 一定程度上影响到整体的预测精度, 今后可以对其组合方式做更深入研究, 以进一步提高整体预测精度.
[1] 李文建. 极端气象条件下金属矿山尾矿库浸润线在线监测系统的设计[D]. 赣州: 江西理工大学, 2013.
[2] 李娟, 李翠平, 李春民, 等. 支持向量回归机在尾矿坝浸润线预测中的应用[J]. 中国安全生产科学技术, 2009, 5(1): 76-79.
[3] 王飞跃. 基于不确定性理论的尾矿坝稳定性分析及综合评价研究[D]. 郑州: 中南大学, 2009.
[4] 邹伟霞, 李慧敏. 基于灰色模型GM(1, 1)的尾矿坝浸润线预测[J]. 现代矿业, 2011(11): 27-29.
[5] 王云海, 李娟, 李春民, 等. 尾矿坝浸润线数据挖掘预测模型的样本选取研究[J]. 中国安全生产科学技术, 2009, 5(5): 9-12.
[6] 王云海, 李春民, 谢旭阳, 等. 粗糙集属性约简在尾矿坝浸润线预测模型中的应用[J]. 金属矿山, 2010(10): 20-23.
[7] 田海雷, 李洪儒, 许葆华. 基于改进人工鱼群算法的支持向量机预测[J]. 计算机工程, 2013, 39(4): 222-225.
[8] 张国华, 张文娟, 薛鹏翔. 小波分析与应用基础[M]. 西安: 西北工业大学出版社, 2006.
[9] 陈吉江, 毛洪翔, 李鹏程, 等. 小波分解高、 低频双自回归模型及其在水质监测中的应用[J]. 水利水运工程学报, 2014(2): 95-99.
[10] 张德丰. Matlab小波分析与工程应用[M]. 北京: 国防工业出版社, 2008: 107-129.
[11] 徐晨, 赵瑞珍, 甘小冰. 小波分析应用算法[M]. 北京: 科学出版社, 2004.
[12] 王应明. 基于相关性的组合预测方法研究[J]. 预测, 2002, 21(2): 58-62.
[13] 肖燕君, 张华, 任若恩. 基于小波多尺度分析的股票价格组合预测方法[J]. 工业工程, 2011, 14(6): 133-137.
[14] 白冬妹, 郭满才, 郭忠升, 等. 时间序列自回归模型在土壤水分预测中的应用研究[J]. 中国水土保持, 2014(2): 42-45.
[15] 晏卫东, 廖宇亮, 刘延青. 基于时间序列分析的导引头误差模型建立方法研究[J]. 自动化技术与应用, 2010, 29(11): 64-68.
[16] 廖寅飞, 刘炯天. 旋流-静态微泡浮选柱分选指标的BP神经网络预测[J]. 煤炭学报, 2012, 37(4): 674-677.
[17] 李建伟, 程晓卿, 秦勇, 等. 基于BP神经网络的城市轨道交通车辆可靠性预测[J]. 中南大学学报(自然科学版), 2013, 44(增刊1): 42-46.
[18] 王旭峰, 沈斐敏. 基于BP神经网络的建筑施工事故非线性组合预测[J]. 福州大学学报(自然科学版), 2015, 43(1): 94-99.
(责任编辑: 沈芸)
Research on infiltration route prediction method based on wavelet multi-resolution-analysis
QIU Kunnan, SHEN Feimin
(College of Civil Engineering, Fuzhou University, Fuzhou, Fujian 350116, China)
In order to improve the prediction precision and the false positives and fail to declare of the tailing dam safety warning, the data is preprocessed by wavelet multi-resolution analysis method, and used Matlab program to achieve the calculation. This paper gives two engineering examples and takes the MAE, MSE, MAPE and MSPE as the evaluation index of the prediction accuracy. The results showed that: the MAE, MSE, MAPE and MSPE of the wavelet multi-resolution analysis model were lower than the other’s. So it can significantly improve the prediction accuracy of forecasting model by wavelet multi-resolution analysis.
infiltration route; wavelet multi-resolution-analysis; non-stationary time series; tailing dam; prediction
10.7631/issn.1000-2243.2016.05.0746
1000-2243(2016)05-0746-07
2015-05-10
沈斐敏(1951-), 教授, 博导, 主要从事事故预测与预防、 安全系统工程等研究, feimshen@sina.com
国家安全监管总局科技基金资助项目(ZY2013-6);福建省自然科学基金资助项目(2011J01297)
TD745.2
A
