基于满意度的区间型多人合作对策在供应链产品合作创新利益分配中的应用

洪防璇， 李登峰

(1. 福州大学经济与管理学院， 福建 福州 350116； 2. 福州大学至诚学院， 福建 福州 350002)

基于满意度的区间型多人合作对策在供应链产品合作创新利益分配中的应用

洪防璇1， 2， 李登峰1

(1. 福州大学经济与管理学院， 福建 福州 350116； 2. 福州大学至诚学院， 福建 福州 350002)

针对区间支付值可能具有嵌套、 重叠和(或)包含关系的供应链产品合作创新利益分配问题， 定义了基于满意度的区间数排序指标. 据此提出区间型多人合作对策的区间值核心解概念和相应的求解方法， 并与区间Shapley值求解方法作对比分析. 通过实例验证了所提方法的可行性和有效性.

供应链管理； 多人合作对策； 区间值核心； 区间数排序

0 引言

供应链产品合作创新有利于供应链上各企业有效整合内外部创新资源， 实现供应链企业间创新资源的共享， 创造更大的利益空间， 但也存在着各种风险和问题， 如道德风险、 合作信任危机、 利益分配不均等. 其中， 利益的合理分配是供应链上企业产品合作创新获得成功并稳定运作的必要条件之一. 在实际的供应链产品合作创新利益分配问题中， 由于决策主体的信息不完全和不确定性、 决策行为的复杂性， 企业联盟收益(即支付值)往往很难获得精确的数值， 通常只能给出大致的估计范围. 比如， 当只能得到最乐观和最悲观情况下的联盟支付值时， 一般采用区间数来描述这些模糊或不精确的信息[1-2]. 这种采用区间数表示企业联盟支付值的多人合作对策即为区间型多人合作对策. 于是， 供应链产品合作创新利益分配问题可以归结为一类区间型多人合作对策问题.

经典的多人合作对策所要解决的一个重要问题就是找到关于合作利益的一个或者一组分配方案， 使得每个局中人都能接受这种利益分配， 并且没有动机和能力改变这种分配状况. 这就是通常所说的多人合作对策的解. 合作对策有多种解的形式， 其中核心是较早提出并广为人们所接受的一种解[3]. 在区间型多人合作对策中， 由于联盟支付值为区间数， 因此不能把经典多人合作对策的核心解直接引入到区间型多人合作对策中. 这里涉及到区间数的运算、 大小比较即排序等问题， 而这些显然不同于实数运算[4].

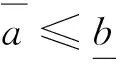
1 区间数及其模糊排序指标

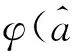
(1)

(2)

不难证明， 区间数排序指标φ具有如下性质：

性质④表示， 定义1给出的区间数模糊排序指标具有传递性.

2 区间型多人合作对策及区间值核心解概念

根据定义3， 可将区间型多人合作对策的区间值核心转化为下述区间型不等式组求解：

(3)

3 基于满意度的区间型多人合作对策求解方法

对于任意一般情况φ∈[0， 1]， 则式(3)可转化为如下的精确型不等式组：

(4)

只要不等式组(4)的解集不为空集， 则区间型多人合作对策存在区间值核心.

类似地， 对于特殊取值φ=0、φ=0+和φ=0.5三种情况， 可做同样探讨.

4 算例分析

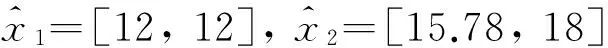
类似地， 对于任意一般情况下的φ∈[0， 1]取给定值， 可求解相应的不等式组， 其解如表1所示.

表1 φ取任意一般情况下的不同给定值时供应链中厂商的利益分配Tab.1 Profit distributions of companies in the supply chain with any general different given φ

表1列出了当φ取一般情况下的不同给定值时供应链中各个厂商(局中人)的利益分配值. 不难发现， 当区间型多人合作对策存在区间值核心时， 各个局中人的分配值仍然是区间数. 随着满意度φ取值越来越高(局中人的要求越来越严格)时， 各个局中人的区间值核心分配可能为空集(在区间值核心的意义下不存在局中人的分配方案)， 这符合了现实条件的逻辑判断.

同样地， 对于特殊取值φ=0、φ=0+和φ=0.5三种情况， 可构建和求解相应不等式组， 均不存在区间值核心.

2) 与改进的区间Shapley值法作对比. 于晓辉等[11]对区间数作一些限制， 提出了改进的区间Shapley值分配方法， 即

(5)

现将式(5)应用上述例子， 并做比较分析. 不难看出， 上述算例中的区间型多人合作对策具有改进的区间Shapley值分配方法所要求的区间有效性、 对称性和超可加性的特点. 因此， 利用式(5)， 可得局中人1的区间Shapley值为[10.33， 17.67]， 即， 供应链中厂商1的利益分配值介于10.33与17.67之间. 同样， 可求出局中人2和3的区间Shapley值分别为区间[11， 17]、 [10.67， 17.33]， 即， 供应链中厂商2和3的利益分配值介于11与17、 10.67与17.33之间.

5 结论

针对供应链产品合作创新中局中人联盟的利益支付值为区间数的情形， 本研究定义基于满意度的区间数模糊排序指标， 构建了区间型多人合作对策区间值核心的求解模型， 提出了相应的求解方法， 并与区间Shapley值法作对比分析. 研究结果表明， 若区间型合作对策存在区间值核心， 则其解的形式仍然是区间数， 符合区间数的定义与运算逻辑， 且该求解方法充分考虑区间数各种排序情况， 求解更为准确. 与经典多人合作对策一样， 区间型多人合作对策的核心也可能是空集(即并非所有的满意度φ值都存在核心)， 也可能存在多个解. 本研究实例由于受到软件求解的制约， 只显示其中的一种解， 而这还需要采用其他方法(比如， 特殊情况时的图解法)才能求解区间值核心中的所有解.

核心只是多人合作对策的一种解形式， 还存在其他解形式. 区间数也只是不确定收益的表现形式之一， 现实生活中还存在其他表示不确定数量的形式， 比如， 三角模糊数等. 另外， 在供应链产品合作创新中， 局中人不仅只考虑短期经济利益的单一目标， 还会考虑企业战略、 企业间合作关系维护、 技术外溢、 长期经济利益等多个目标. 这些问题都有待于将来作进一步的深入研究.

[1] ALPARSLAN G. Some results on cooperative interval games[J]. Optimization， 2014， 63(1): 7-13.

[2] ALPARSLAN-GÖK S Z， BRANZEI O， BRANZEI R，etal. Set-valued solution concepts using interval-type payoffs for interval games[J]. Journal of Mathematical Economics， 2011， 47(4/5): 621-626.

[3] GILLIES D. Solution to general non-zero-sun games[J]. Contributions to the Theory of Games， 1959， 4: 47-85.

[4] MOORE R. Methods and applications of interval analysis[M]. Philadelphia: SIAM ， 1979.

[5] ISHIHUCHI H， TANAKA H. Multiobjective programming in optimization of the interval objective function[J]. European Journal of Operation Research， 1990， 48(2): 219-225.

[6] NAKAHARA Y， SASAKI M， GEN M. On the linear programming problems with interval coefficients[J]. Computer and Industrial Engineering， 1992， 23(1/2/3/4): 301-304.

[7] SENGUTA A， PAL T K. On comparing interval numbers[J]. European Journal of Operation Research， 2000， 127(1)： 28-43.

[8] LI D F， NAN J X， ZHANG M J. Interval programming models for matrix games with interval payoffs[J]. Optimization Methods and Software， 2012， 27(1): 1-16.

[9] GUAN F， XIE D Y， ZHANG Q. Solutions for generalized interval cooperative games[J]. Journal of Intelligent and Fuzzy Systems， 2015， 28(4): 1 553-1 564.

[10]MENG F Y， ZENG X L， Li Z Y. Research the priority methods of interval numbers complementary judgment matrix[J]. International Conference on Grey System and Intelligent Services， 2007， 1: 42-47.

[11] 于晓辉， 张强. 基于区间Shapley值的生产合作利益分配研究[J]. 北京理工大学学报， 2008， 28(7): 655-658.

[12] 谭春桥， 张强. 具有区间联盟值n人对策的Shapley值[J]. 应用数学学报， 2010， 33(2): 193-203.

[13] MENG F Y， CHEN X H， TAN C Q. Cooperative fuzzy games with interval characteristic functions[J]. Operational Research， 2016， 16(1): 1-24.

[14] MENG F Y， ZHANG Q， WANG Y. Cooperative fuzzy games with a coalition structure and interval payoffs[J]. International Journal of Computational Intelligence Systems， 2013， 6(3): 548-558.

(责任编辑： 林晓)

Interval-valued many-person cooperation games based on satisfactory degree with application to profit distribution of product cooperative innovation in the supply chain

HONG Fangxuan1， 2， LI Dengfeng1

(1. School of Economics and Management， Fuzhou University， Fuzhou， Fujian 350116， China;>2. Zhicheng College， Fuzhou University， Fuzhou， Fujian 350002， China)

With regard to a problem of profit distribution of product cooperative innovation in the supply chain with the interval payoffs of inclusion and/or overlap relations， a satisfactory degree of comparing intervals is defined. Hereby， the concept of interval core of interval-valued many-person cooperation games and corresponding solving methods are proposed， which compared with the solving method of interval Shapley value. The feasibility and applicability of this method is illustrated with a numerical example.

supply chain management; many-person cooperation game; interval core; interval ranking

10.7631/issn.1000-2243.2016.05.0616

1000-2243(2016)05-0616-05

2016-01-22

李登峰( 1965- ), 教授, 主要从事经济管理决策与对策、 运筹管理等方面研究， lidengfeng@fzu.edu.cn

国家自然科学基金资助项目(71231003); 福建省社会科学规划资助项目(FJ2015B185); 福建省中青年教师教育科研资助项目(JA13392S); 福州大学社科科研扶持基金资助项目(15SKF13); 福建省高校杰出青年科研人才培育计划资助项目(闽教科[2015]54号)； 福建省高校科技创新团队支持计划资助项目(闽教科[2012]3号)

F272

A