有限需求分布信息下损失厌恶的报童模型研究

阳成虎， 刘兰英， 赵一民

(福州大学经济与管理学院， 福建 福州 350116)

有限需求分布信息下损失厌恶的报童模型研究

阳成虎， 刘兰英， 赵一民

(福州大学经济与管理学院， 福建 福州 350116)

考虑有限需求分布信息下具有损失厌恶特性的报童订货策略问题. 在前景理论框架下， 基于最小最大后悔值准则建立了仅知需求区间信息下的报童鲁棒订货模型， 分析了损失厌恶系数， 单位剩余损失以及需求区间范围对损失厌恶报童鲁棒订货量和最小最大后悔值的影响. 研究结果表明： 决策者的鲁棒订货量随单位剩余损失的增大而减少， 但随着损失厌恶系数和需求区间范围的增大， 鲁棒订货量可能增大也可能减少， 决策者的最小最大后悔值总是随厌恶系数和需求区间范围的增大而增大， 随单位剩余损失的增大而减小.

报童模型； 损失厌恶； 前景理论； 最小最大后悔值准则

0 引言

报童模型作为随机库存理论的基础模型， 已经成为研究库存管理、 收益管理、 期权定价和供应链协调等问题的重要工具. 传统的报童模型研究决策者在需求分布完全已知的情况下确定最优订货量使期望利润最大化. 然而， 随着科技的发展和消费者选择的多样性， 电脑、 软件等创新性产品和服装、 玩具等季节性产品的生命周期逐渐缩短， 决策者在实际经营中掌握的历史销售数据十分有限. 这使得决策者往往无法根据历史数据准确预测产品的需求分布， 或者为获得准确需求分布投入的成本大于潜在收益. 大多数情况下， 决策者通过历史数据仅仅能得到产品需求分布的区间、 均值或方差等有限信息. 其中， 采用区间信息是描述有限需求分布信息的一种常见方式.

目前， 基于有限需求分布信息的报童问题已经引起了学者的重视， 并取得了不少研究成果. Scarf等[1]最早研究了在仅知均值和方差信息情形下的自由分布报童订货问题， 提出了最小最大化(min-max)方法， 即寻求最坏需求分布下的最优订货策略. 此后， 该方法应用于不同运作环境下的报童问题[2-3]. 此外， Andersson等[4]在研究单周期的有限需求分布信息下的报童问题时， 利用极大熵方法得到需求的先验分布， 并将由此得到的最优解与最小最大化方法得到的最优解进行了比较.

上述两种方法较好地解决了有限需求分布信息下的报童订货决策问题， 但存在一些不足， 如最小最大化方法得到的两点分布在现实中发生的概率很小， 牺牲了决策者的部分利润； 根据极大熵方法得到的解不像最小最大化方法那样保守， 较适用于风险中性决策者. 相对于以上两种方法， Savage[5]提出的最小最大后悔值方法是更为稳健的方法. 该方法目的是使决策者为获取需求分布完整信息的最大投入的最小化. Vairaktarakis[6]采用该方法研究了仅知区间信息下报童的鲁棒订货策略. Perakis等[7]基于最小最大后悔值准则求解了以下八种有限需求信息结构下的报童鲁棒订货量及后悔值. 此外， Yue等[8]和Jiang等[9]运用最小最大后悔值准则探讨了不同运作环境下报童的鲁棒订货策略.

上述文献对有限需求分布信息下报童问题的研究通常假设决策者是完全理性人， 忽视了决策者的行为特征. 在实际中， 市场环境复杂， 订货决策过程受决策者的认知能力、 行为偏差等因素的影响， 存在非理性和有限理性行为， 导致理论结果与实际运作情况存在较大的偏差[10-11]. 近年来， 学者们将决策者不同的行为偏好引入到报童问题的研究， 如过度自信、 损失厌恶、 有限理性和锚定效应[12-15]. 其中损失厌恶是研究中最常见的行为偏好. 现实中的部分决策者， 特别是规模较小的决策者厌恶损失， 即他们可能不仅仅只关注利润最大化， 同样会关注由于缺货或库存过剩所带来的损失[16].

目前， 研究损失厌恶报童问题的多采用期望效用理论， 不少学者进行了相关研究[17]. 但是， 期望效用理论在描述个体决策行为上存在缺陷， 在此框架下得到的报童模型的解具有一定的局限性. 在期望效用理论的基础上， Kanneman等[18]提出了前景理论. 他们发现： 现实中大多数人对损失和收益的敏感程度是不一致的， 损失带给人们的痛苦要大于相同收益给人们带来的快乐. 目前， 前景理论已广泛应用于证券、 股票、 保险、 市场营销等领域. 已有学者基于前景理论对损失厌恶报童问题进行了研究. Wang等[16]、 文平[19]和周艳菊等[20]研究了不同市场环境下报童的鲁棒订货策略. 此外， 林志炳等[21]和李绩才等[22]在研究不同类型的供应链契约时， 采用前景理论分析了损失厌恶的决策主体的订货决策.

上述文献仅考虑了有限需求分布信息和损失厌恶的行为偏好中的一种， 并没有分析这两种情形对最优订货决策的综合影响. 本文结合前景理论和鲁棒优化理论， 分别考虑需求区间信息和决策者损失厌恶的行为偏好， 基于最小最大后悔值准则建立报童鲁棒订货模型， 求解不考虑缺货惩罚和考虑缺货惩罚时的鲁棒订货策略， 并分析损失厌恶系数和单位剩余损失对鲁棒订货量和最小最大后悔值的影响.

1 问题描述

考虑一个销售季节性产品的损失厌恶报童， 需要在销售季节到来之前确定订货量q. 报童面对随机需求为x的市场， 只有一次订货机会. 若订货量大于市场需求则超出部分只能在季末以很低的价格处理； 若订货量小于市场需求则会产生一定的缺货损失. 假设产品的市场需求x连续非负， 其概率密度函数为f(x)， 累积分布函数F(x)， 属于具有相同定义域[A,B]的某一类凸分布集合ψ， 但具体的分布函数是未知的.

为了刻画报童的损失厌恶特性， 采用如下分段线性函数[21]：

(1)

其中:W0为决策者的参考点(可认为初始财富值)， 不失一般性， 假设W0=0;λ为损失厌恶系数， 表示决策者对损失的厌恶程度,λ越大， 决策者的损失厌恶程度越高, 一般情况下，λ取值为2.25[23]. 此外， 在竞争激烈的零售商业环境下， 决策者可能会更关注实际损失. 即， 相比缺货带来的机会损失， 决策者会更重视库存积压带来的资金占用和存货品质的下降[24]. 因此， 假设决策者是实际损失厌恶型， 且实际损失和机会损失给决策者带来的负效用不同. 令决策者对期望剩余损失和期望缺货损失的厌恶系数分别为λ1和λ2， 且λ1>λ2.

其它符号及参数定义如下：r: 产品的单位零售价；s: 销售期结束后单位剩余产品的残值；l: 单位缺货惩罚；c: 单位采购成本；q: 基于部分信息下的报童订货量,EUF(q)为相应的期望效用值；Q: 完全信息下的报童订货量,EUF(Q)为相应的期望效用值；ρ: 后悔值.

2 模型构建及分析

基于上述的分析和假设， 决策者的收益函数为：

(2)

对式(2)分两种情况进行讨论.

1) 当q≥x时， 令rx+s(q-x)-cq=0， 得盈亏平衡点qt1=(c-s)q/(r-s). 即， 需求x=qt1时， 收益为零； 需求x∈[A,qt1]时， 收益为负； 需求x∈[qt1,q]时， 收益为正.

2) 当q≤x时， 令rq-l(x-q)-cq=0， 得盈亏平衡点qt2=(r+l-c)q/l. 即， 需求x=qt2时， 收益为零； 需求x∈[q,qt2]时， 收益为正； 需求x∈[qt2,B]时， 收益为负.

根据上述分析， 当实际需求x∈[A,qt1]时， 决策者将面临剩余损失； 当实际需求x∈[qt2,B]时， 决策者将面临缺货损失.

综合以上两种情况， 基于前景理论的期望效用为：

(3)

不失一般性， 对式(3)进行标准化处理. 令r+l-s=1，α=r-s，β=c-s， 其中α为单位缺货损失，β为单位剩余损失. 则式(3)可以转化为：

(4)

(5)

ρ(q)可理解为决策者为获得完整的市场需求分布信息愿意付出的最大成本. 依据最小最大化后悔值准则， 决策者应该使这项最大成本最小化， 即最小化ρ(q). 此时，

(6)

引理1 1) 函数G(Q;q)在区间Q∈[0,q]和区间Q∈[q, ∞)上均是凹函数， 但在区间Q∈[0, ∞)上并不一定是凹函数；

2) 函数ρ(q)是凸函数， 则鲁棒订货量q*=argminρ(q)， 且满足如下等式：

引理1的前一部分表明, 在求解式(4)时， 应考虑Q≤q和Q≥q两种情况； 后一部分表明, 当由于实际订货过多(对应Q≤q)产生的负效用值和实际订货过少(对应Q≥q)产生的负效用值相等时， 鲁棒订货量q*能够使最大后悔值最小化.

根据上述引理， 鲁棒订货量和相应的最小最大后悔值可以由如下定理给出.

定理1 对于任意非负累积分布函数F∈ψ， 在仅知需求区间[A,B]的条件下， 基于最小最大后悔值准则的损失厌恶报童的鲁棒订货量q*为：

(7)

最小最大后悔值为(证明见附录)：

(8)

由定理1可知， 鲁棒订货量q*不依赖于任何分布， 只与损失厌恶系数λ1和λ2、 需求区间[A,B]以及单位剩余损失β有关.

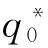
根据定理1， 可以得到不考虑缺货惩罚时损失厌恶报童的鲁棒订货量及相应的最小最大后悔值， 结论如下.

推论1 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 基于最小最大后悔值准则， 不考虑缺货损失时损失厌恶报童的鲁棒订货量为：

(9)

最小最大后悔值为：

(10)

证明 当没有缺货惩罚(即l=0)时， 报童不再考虑缺货所带来的损失， 则缺货损失厌恶系数λ2退化为1. 令式(7)和式(8)中λ2=1即可得到如上结论. 证毕.

推论1表明没有缺货惩罚的情形是考虑缺货惩罚情形的一个特例.

下面讨论损失厌恶系数λ1和λ2， 区间范围[A,B]及单位剩余损失β对报童的鲁棒订货量和最小最大后悔值的影响， 有以下结论：

推论2 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 损失厌恶报童的鲁棒订货量随剩余损失厌恶系数λ1的增大而减少， 随缺货损失厌恶系数λ2的增大而增大.

证明 分别对鲁棒订货量q*关于λ1和λ2求一阶偏导， 得到：

可以看出，q*关于λ1单调递增， 关于λ2单调递减.

推论2表明不完全信息下， 决策者不同的损失偏好对其鲁棒订货量的影响不相同. 若决策者更加厌恶剩余损失， 当其它条件不变时， 鲁棒订货量会随着剩余损失厌恶程度增加而减少. 特别是， 当λ1趋于无穷时，q*趋近于A. 这表明当决策者对剩余损失极度厌恶时， 会选择订购最少数量的产品. 若决策者更加厌恶缺货损失， 当其它条件不变时， 鲁棒订货量会随着缺货损失厌恶程度增加而增大. 特别是， 当λ2趋于无穷时，q*趋近于B. 这表明当决策者对缺货损失极度厌恶时， 会选择订购尽可能多的产品.

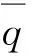
推论3 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 损失厌恶报童的最小最大后悔值均随着厌恶系数λ1和λ2的增大而增大.

证明 对报童的最小最大后悔值ρ*分别关于λ1和λ2求一阶偏导， 得到：

显然，ρ*关于λ1和λ2均单调递增. 证毕.

推论4 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 损失厌恶报童的鲁棒订货量随单位剩余损失β的增大而减少.

证明 首先对式(5)关于β求一阶偏导， 可得：

因此， 鲁棒订货量q*与单位剩余损失β具有负相关关系. 证毕.

推论4表明， 产品的单位剩余损失越大， 可能产生的剩余损失也就越大， 所以报童会减少订货量以降低库存. 这与损失中性情形下的性质一致. 特别地， 当β趋近于0时，q*趋近于需求区间的上限B； 当β趋近于1时，q*趋近于需求区间的下限A.

推论5 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 随需求区间范围的增大， 损失厌恶报童的鲁棒订货量可能增大也可能减少.

需求分布的区间大小表明决策者掌握需求信息的准确性. 显然区间越小说明掌握的信息越准确. 推论5表明决策者的鲁棒订货量与其掌握的区间信息准确程度没有必然联系. 当决策者掌握较为准确的区间信息时， 其鲁棒订货量可能增大也可能减少.

推论6 对于区间[A,B]上的任意非负累积分布函数F∈ψ， 损失厌恶报童的最小最大后悔值随需求区间范围的增大而增大.

证明 对式(6)关于(B-A)求一阶偏导， 可得

因此， 报童的最小最大后悔值与需求区间范围(B-A)正相关. 证毕.

由推论6可以看出， 决策者掌握的信息越准确， 后悔值越小， 说明其做出的订货决策越优. 这与损失中性情形下的性质一致. 特别地， 若A=B， 决策者恰好准确预测市场的需求量， 则其的后悔值为零.

3 结语

研究了需求分布未知情形下损失厌恶报童的订货策略. 基于前景理论， 采用最小最大后悔值准则建立了仅知需求区间信息下损失厌恶的报童模型， 给出了报童鲁棒订货量和相应的最小最大后悔值的解析表达式， 并分析了损失厌恶系数， 单位剩余损失以及需求区间范围对损失厌恶报童鲁棒订货量和最小最大后悔值的影响. 扩展了Perakis等[7]的研究结果， 其得到的损失中性报童的鲁棒订货策略是本文结果的一个特例. 特别是， 若实际损失和机会损失给决策者带来的负效用相同， 损失厌恶报童的鲁棒订货量与损失厌恶系数无关， 仍为损失中性报童的鲁棒订货量.

今后可以进一步扩展研究， 如采用最小最大后悔值准则解决其他需求信息(如均值、 方差、 中位数)情形下损失厌恶的报童模型， 并将这类模型扩展到需求受价格影响的情形.

附录：

定理1的证明.

对式(6)， 应首先考虑如下的内层优化问题：

将上式分解为以下三个部分进行分析：

根据引理1， 分别考察Q≤q和Q≥q两种情况.

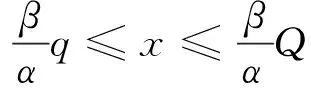
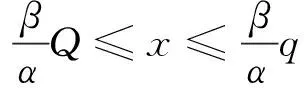
2.1)Q≥q. 同1.1)分析可得，

2.2)Q≤q. 同1.2)分析可得，

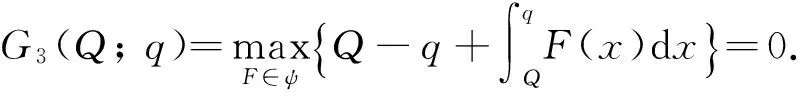
综上所述， 当Q≥q时，

GP(Q;q)=G1(Q;q)+G2(Q;q)+G3(Q;q)=[βλ1+(1-β)λ2](Q-q)

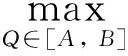
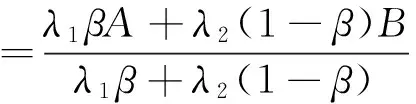
[1]SCARFH.Amin-maxsolutionofaninventoryproblem[M]//ARROWK,KARLINS,SCARFH.StudiesintheMathematicalTheoryofInventoryandProduction.Stanford:StanfordUniversityPress, 1958.

[2]GALLEGOG,MOONI.Thedistributionfreenewsboyproblem:reviewandextensions[J].JournalofOperationalResearchSociety, 1993, 44(8): 825-834.

[3]YUH,ZHAIJ.Thedistribution-freenewsvendorproblemwithbalkingandpenaltiesforbalkingandstockout[J].JournalofSystemsScienceandSystemsEngineering, 2014, 23(2): 153-175.

[4]ANDERSSONJ,JORNSTENK,NONASSL,etal. A maximum entropy approach to the newsvendor problem with partial information[J]. European Journal of Operational Research, 2013, 228(1): 190-200.

[5] SAVAGE L. The theory of statistical decision[J]. Journal of the American Statistical Association, 1951, 46(253): 55-67.

[6] VAIRAKTARAKIS G L. Robust multi-item newsboy models with a budget constraint[J]. International Journal of Production Economics, 2000, 66(3): 213-226.

[7] PERAKIS G, ROELS G. Regret in the newsvendor model with partial information[J]. Operation Research, 2008, 56(1): 188-203.[8] YUE J F, CHEN B T, WANG M C. Expected value of distribution information for the newsvendor problem[J]. Operation Research, 2006, 54(6): 1 128-1 136.

[9] JIANG H, NETESSINE S, SAVIN S. Robust newsvendor competition under asymmetric information[J]. Operations Research, 2011, 59(1): 254-261.

[10] SU X. Bounded rationality in newsvendor models[J]. Manufacturing & Service Operations Management, 2008, 10(4): 566-589.

[11] 刘作仪， 查勇. 行为运作管理： 一个正在显现的研究领域[J]. 管理科学学报， 2009， 12(4)： 64-74.

[12] 柳键， 邱国斌， 黄健. 考虑缺货损失情形下损失厌恶零售商的订货决策[J]. 控制与决策， 2012， 27(8)： 1 195-1 200.

[13] 谢勇， 孟楚， 王红卫. 过度自信的报童模型研究[J]. 工业工程， 2013， 16(4)： 38-43.

[14] 宋鸿芳， 冉伦， 褚宏睿， 等. 基于有限理性的供应链库存控制[J]. 预测， 2014， 33(2)： 55-58.

[15] 宋鸿芳， 冉伦， 褚宏睿， 等. 消费者锚定效应下的动态定价与库存控制研究[J]. 中国管理科学， 2015， 23(4)： 123-128.

[16] WANG C X, WEBSTER S. The loss-averse newsvendor problem[J]. Omega, 2009, 37(3): 93-105.

[17] AGRAWAL V, SESHADRI S. Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem[J]. Manufacture & Service Operation Management, 2000, 2(4): 410-423.

[18] KANNEMAN D, TVERSKY A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291.

[19] 文平. 损失厌恶的报童-预期理论下的报童问题新解[J]. 中国管理科学， 2005， 13(6)： 64-68.

[20] 周艳菊， 应仁仁， 陈晓红， 等. 基于前景理论的两产品报童的订货模型[J]. 管理科学学报， 2013， 16(11)： 17-29.

[21] 林志炳， 蔡晨， 许保光. 损失厌恶下的供应链收益共享契约研究[J]. 管理科学学报， 2010， 13(8)： 33-41.

[22] 李绩才， 周永务， 肖旦， 等. 考虑损失厌恶一对多型供应链的收益共享契约[J]. 管理科学学报， 2013， 16(2)： 71-82.

[23] 邹燕， 郭菊娥. 对期望理论的两个重要推进-损失厌恶系数λ及参考点研究[J]. 运筹与管理， 2007， 16(5)： 87-89.

[24] 周艳菊， 邱菀华， 王宗润. 损失约束下多产品报童问题的求解方法研究[J]. 控制与决策， 2007， 22(9)： 1 005-1 010.

[25] 谭建， 王先甲. 缺货惩罚下的损失厌恶报童模型[J]. 武汉大学学报(工学版)， 2010， 43(5)： 677-680.

(责任编辑： 洪江星)

Loss-averse newsvendor model with partial demand information

YANG Chenghu, LIU Lanying, ZHAO Yimin

(School of Economics and Management, Fuzhou University, Fuzhou, Fujian 350116, China)

A loss-averse newsvendor’s robust order decision is studied when partial information of demand distribution is available. In the framework of prospect theory, the robust newsvendor model is developed based on the minimax regret criterion. Accordingly, the robust order quantity is derived in the closed-form expression. In addition, the effects of loss aversion coefficient, unit overage loss and the support on the robust order quantity and minimax regret are analyzed. The results show that the robust order quantity decreases with unit overage loss increasing. With the loss aversion coefficient and the support increasing, the robust order quantity is not monotonous. The results also show that the minimax regret value increases with the loss aversion coefficient and the support increasing, but deceases with unit overage loss increasing. Finally, numerical samples are conducted to verify the relationships of the robust order quantity and minimax regret value with loss aversion coefficient, unit overage loss and the support.

newsvendor model; loss aversion; prospect theory; minimax regret criterion

10.7631/issn.1000-2243.2016.05.0609

1000-2243(2016)05-0609-07

2015-07-08

阳成虎(1980-), 副教授, 博士, 主要从事物流系统建模与优化方面的研究, hcysun@126.com

国家社会科学基金青年资助项目(12CGL045)； 中国博士后科学基金资助项目(2013M531541)； 福建省高校杰出青年科研人才培养计划(JA12037S)

F273

A