浅析利用“四步法”预测ABnm型微粒的空间构型

邵斅农

摘 要： 普通高中新课程标准化学【人教版.选修③】模块中对判断和推断常见的多原子微粒的立体结构，特别是预测ABⁿ_m型微粒的空间构型是近年来高考考查的重点之一，但是对于初学者来说总是一大难题。本文就针对这一难题介绍一种较为快速、准确的预测出ABⁿ_m型微粒的空间构型的方法——“四步法”。

关键词： 四步法 ABⁿ_m型 微粒 空间构型

从近几年新课标地区“物质结构与性质”模块的高考试题分析考查微粒空间构型主要以ABⁿ_m型为主且趋于稳定。对于初学者来说，该部分内容相对较难掌握，因而容易产生困惑和误解；为此，接下来就选NH、CO、SO 、 HO 、NH 、 SF这六种微粒为具体的实例浅析预测ABⁿ_m型微粒空间构型过程中“四步法”的灵活应用。【说明：其中A代表中心原子，B代表与中心原子结合的原子，n代表为微粒所带电荷。且n=0说明微粒 ABⁿ_m为分子，n>0则微粒 ABⁿ_m代表的是阳离子、n<0时微粒 ABⁿ_m代表的是阴离子。】

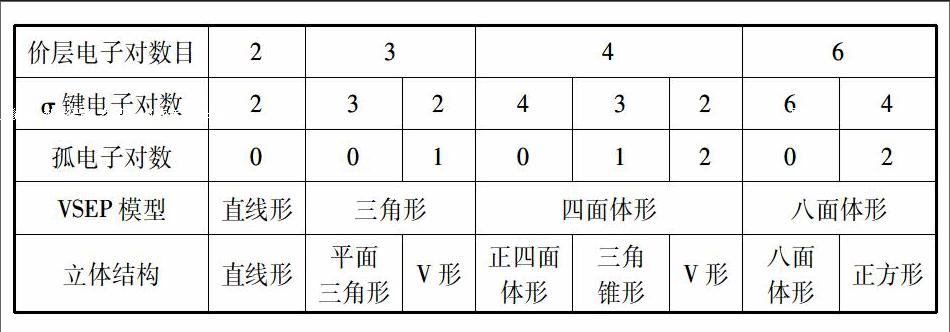
1.“四步法”预测ABⁿ_m型微粒空间构型具体实施步骤

1.1第一步：根据电子式或结构式确定ABⁿ_m型微粒的中心原子

针对ABⁿ_m型微粒一般来说中心原子就为A

1.2第二步：计算中心原子A含有的孤电子对数

中心原子A含有的孤电子对数=1/2（a-xb）

【说明：a代表中心原子价电子数；对于主族元素，a等于最外层电子数，对于阳离子来说，a等于价电子数减去离子所带的电荷数；对于阴离子来说，a等于价电子数加上离子的电荷数的绝对值。 b代表与中心原子结合的原子最多能接受的电子数；其中氢为1，其他原子等于8减去该原子的价电子数。 x代表与中心原子结合的原子个数。】

1.3第三步：计算ABⁿ_m型微粒的价层电子对数

ABⁿ_m型微粒的价层电子对数=中心原子A的孤电子对数+σ键电子对数

1.4第四步：根据ABⁿ_m型微粒的价层电子对数确定VSEPR构型并结合中心原子A的孤电子对数的确定该微粒的立体构型

2.以NH、CO、SO 、 HO 、NH 、 SF为实例预测ABⁿ_m型微粒空间构型中 “四步法”的灵活应用

2.1确定微粒的中心原子

NH、CO、SO、 HO、NH、SF微粒的中心原子分别为N、C、O、S、 O 、N、S

2.2确定中心原子A的孤电子对数

2.3确定价层电子对数

2.4结合上述步骤四中的有关结论确定ABⁿ_m型微粒的立体构型

“四步法”主要适用于常见ABⁿ_m型微粒空间构型的预测，但对于不常见或比较复杂的微粒空间构型的预测“四步法”并不适用，此时最好应用等电子体原理预测一些不常见或比较复杂微粒的空间构型。因为等电子体分子轨道中的电子排布和成键情况相似因而微粒空间结构相同，根据等电子这一原理可推知，原子数目相同的离子或分子中，若电子数也相同，电子排布和成键情况相似，则这些分子或离子就具有相同的电子结构同时具有相似的几何构型。如简单的CO分子的空间构型属于直线形，不常见的N离子与CO分子属于等电子体二者的结构相似，则N与CO微粒空间构型应该相似且都属于直线型；同理复杂离子NO与BF属于等电子体，根据等电子体原理可知二者的结构相似且微粒空间构型都属于平面三角形。

参考文献：

[1]陈经涛，吕俊芳.分子或离子的空间构型与杂化方式的简易确定法[J].陕西教育学院学报，2003，19（1）.

[2]葛尚正.判断分子空间构型的简便方法[J].山东化工，.2003，32（9）.

[3]勾华.在教学中使用价层电子对互斥理论的探讨[J].贵州师范大学学报，1999，17（1）.

[4]谭长森.用等电子体原理预测未知物的空间空间构型[J].四川师范学院学报，1991，12（3）：287-289.

[5]朱斌.杂化轨道理论与价层电子对互斥理论应用于分子构型的比较研究[J].四川师范学院学报，2003，24（2）.