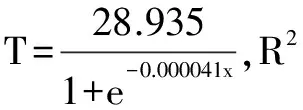基于拉弗曲线的广东省财政收入合理性分析
2016-03-13刘炯宇何学聪
刘炯宇 何学聪
(广东外语外贸大学,广东 广州 510000)
1 导论
1.1 研究的意义和目的
财政是政府为了履行其职能,而通过各种途径筹集的可支配社会资源。在现代中国,财政收入包括税收、各种基金收入、国有企业收入、发行债务收入以及行政收入等等。财政收入的规模,体现了政府参与社会资源分配的规模。财政收入规模的大小,对社会经济的发展和财政自身的发展均有重要的反作用。财政收入过大,会加重社会税负,打压社会工作积极性,限制社会经济发展。而财政收入太小,则会导致政府赤字过大,无法正常履行职能,为社会提供必需的公共服务,最终也不利于社会经济的健康发展。因此,一个适度的财政收入规模是经济健康发展的前提。从地方的角度看,地方经济的发展同样需要一个适度的地方财政收入规模。而目前,对于广东财政收入规模合理性,存在多种说法。其中,较多的民间人士认为,政府税负过重,政府行政费用过大,财政收入规模不合理。而不少专家学者则认为,广东正处于经济结构调整转型期间,应该保持较大的财政收入规模来保证政府在转型中得推进作用。而且,在土地财政日益减少、地方债发行规模过大的情况下,政府应该寻找新的财政收入来源。当然,也有不少学者认为,财政之外的其他政府职能部门所筹集的资金没有纳入财政收入,政府所掌握的资源没有完全反映出来。
为了让财政收入更好为经济发展服务,研究广东财政收入规模是否合理有其必要性和重要性。本文将利用拉弗曲线对广东省财政收入规模与广东省GDP的关系进行研究,进而判断当前财政收入规模是否合理。
1.2 国内外研究现状
“拉弗曲线”理论是由“供给学派”代表人物、美国南加利福尼亚商学研究生院教授阿瑟·拉弗提出的。该曲线描述了社会GDP与税率之间的关系:当税率在一定范围內时,加大税率可以促进GDP增长。而当税率超过了这个范围之后,加大税率反而会导致GDP下降。该曲线很好地描述了财政收入与社会经济的相互作用关系,很容易在理论上给以证明。然而,拉弗曲线的局限性在于,它只是一个大概的模型,描述了这样的一种趋势,并没有给出具体的函数模型。因此,即使有了这个理论,经济学家们还是要争论现有的税率到底是在最有税率的左侧或是右侧。所以,如果我们要使用该曲线,必须找到可以用于描述该曲线的函数表达式。《适度财政收入研究》的作者刘锐运用状态空间模型来将拉弗曲线动态地表示出来,估计了我国最优宏观税负水平。在《最优财政收入规模问题研究评析》一文中,作者姚绍学博士认为从长期来看,政府所做出的宏观税负率并不会偏离最优宏观税负率太远,因此对某一地区的宏观税负率和当地的人均GDP进行回归分析,得到的函数表达式便是当地最优宏观税负率和人均GDP的关系式。姚绍学利用各国历史数据拟合出具体的函数表达式,从而使拉弗曲线可以被用于具体分析。这种方法不仅克服了拉弗曲线没有具体表达式的局限,而且克服了拉弗曲线中,忽略财政政策对社会经济的反作用的缺点,将拉弗曲线动态地表示出来。本文也将使用这种方法来判断广东财政收入规模的合理性。
1.3 本文研究思路
本文首先参考姚绍学博士在《最优财政收入规模问题研究评析》的成果,分别使用Logistic和Compertz函数对广东省历年来的宏观税负率数据和GDP进行拟合,选出其中拟合程度较好的一个,作为广东省最优宏观税负率和广东省GDP的关系式,然后通过这个关系式,计算出当前广东省GDP水平下的最优宏观税负率,与实际数据进行比较,得出结论。在最后一部分,笔者将针对所得结论,通过与其他经济发展程度相仿的省市、国家的情况进行比较,分析内在的原因,并提出建议。本文最后将提出广东实现最优财政收入规模的对策。
2 拉弗曲线及其推广
2.1 拉弗曲线
对宏观税负与经济关系的研究是西方公共经济学和财政学的重要内容,而有重要影响的当推美国供给学派的代表人物阿瑟·拉弗提出的有关税收负担与税收收入或经济关系的曲线,即“拉弗曲线”,拉弗曲线的示意图如图1所示。
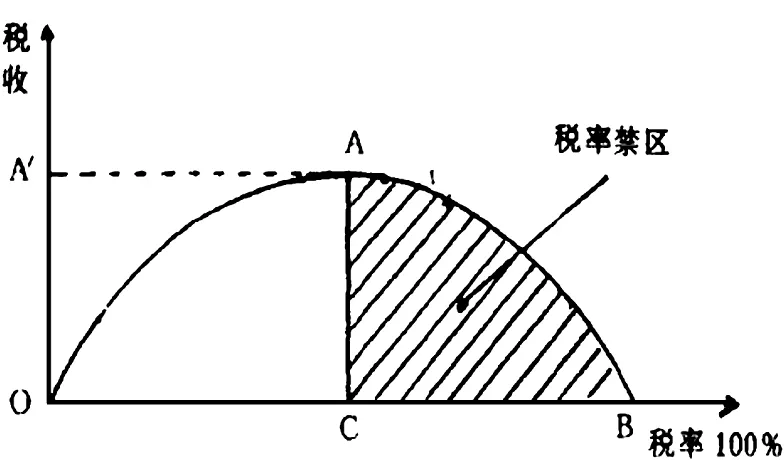
图1 拉弗曲线
不难发现,拉弗曲线揭示的规律可以总结为:初期时,税率的提升可以提高政府税收的收入。但是随着税率的提高,高税率对国民经济的负面作用便开始显现。寻子员提出:“在高税率上,人们逃避纳税现象增多,人们这时宁可用闲暇替换收入,用消费替换储蓄和投资,或寻求税收的漏洞将生产转到地下,这将影响经济的发展”。
于是我们可以发现,随着税率的进一步提高,高税收不能带来更高的税收收入,反而会影响国民经济的发展导致税收下降。因此,理论上便存在着最优税率点,在最优税率点右边的区域我们称之为税率禁区。
改革现状 针对以上问题,国内众多院校在该课程的教研教改上做了大量的研究工作以提高课程的教学质量,加强课程体系的建设。
2.2 拉弗曲线推广
拉弗曲线给我们揭示了税率和税收收入之间的关系,并且理论上提出了最优税率点的存在,但是拉弗曲线只是对这种关系进行了“一般”性的描述而没有严格的数学证明。在这一方面做出了突破,把原本停留在理论层面的拉弗曲线运用在实际数据分析的是姚绍学。
拉弗曲线的一个缺点是它是一个静态模型,它所反映的是在一个时点或者极短的时间下,税收收入和税率之间的关系,并且得出唯一的最优税率。但是我们都知道,经济的发展是迅速的,在每一个具体的经济规模下的确存在着拉弗曲线反映的关系和唯一的最优税率,可是我们不能把一个某一具体经济规模下的最优税率当成是另一经济规模下的最优税率。也就是说:最优税率是随着经济的发展不断变化的,最优税率和经济发展水平存在着一种确定的关系。姚绍学的拉弗曲线拓展便是为了找到最优税率和经济发展之间的函数关系,通过研究,他认为最优税率和经济水平的关系如图2所示。
随着经济水平的提高,最优税率也会不断提高,然后趋向于某一特定的值,这个值我们称为宏观税负率极限值,记为K。为了得出这个反应最优宏观税负率和经济发展水平的函数L,姚绍学对24个国家宏观税负率和人均GDP的时间序列数据的关系进行了模型的估计和检验、发现,一般规律而言,各国的最优宏观税负率的变动随经济水平呈现Logistic函数或者Compertz函数关系。
至此,我们把静态的拉弗曲线推广到了动态模型,并且得出了最优宏观税负率和经济发展水平之间的函数关系,即符合Logistic函数或者Compertz函数关系。
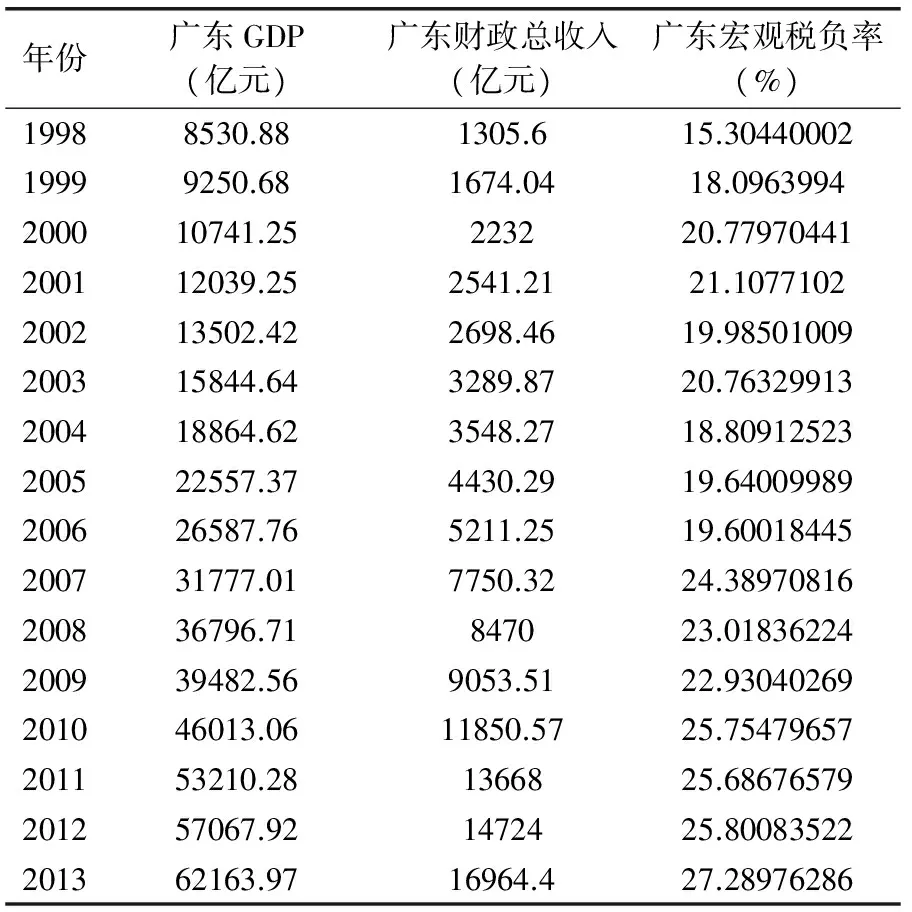
表1 广东历年的财政总收入、宏观税负率和GDP数据
资料来源:各年份《广东省统计年鉴》。
3 广东省宏观税负率与GDP的回归分析
3.1 财政收入与宏观税负的概念界定
宏观税收负担是指一个国家或地区在一定时间内税收总收入占社会总产出的比重。国外一般使用税收收入占GDP比重来反映。但是在中国,由于政府税收不规范,税收以外的收入比重较大,单纯使用税收收入占GDP比重这个指标不能很好地反映广东经济的税负。我国财政收入有多种口径,不同统计口径的财政收入会导致不同的结果。我国税收收入分为两部分,一部分归地方政府,称为地税;一部分归中央,称为国税。除了税收以外,还包括行政费用、基金收入、国企收入、地方债收入。为了更好地体现财政收入与地方经济发展之间的关系,我们以“大口径法”来统计广东的财政总收入。“大口径法”是以政府所有的税收收入和非税收收入来界定政府的财政收入,不仅包括来源于广东的所有税收收入,还包括来源于广东的、政府各级部门向企业和个人所征收的不纳入政府一般预算的预算外收入,以及没有纳入预算外管理的制度外收入等等。
宏观税负率=财政总收入/当期GDP
广东历年的财政总收入、宏观税负率和GDP数据如表3所示。为了使结果更具有代表性,我们选取了最近16年的数据(2014年的数据尚未统计出来)。
3.2 基于Logistic曲线回归分析
logistic回归又称logistic回归分析,主要在流行病学中应用较多。姚绍学将其运用在构建最优宏观税负率和经济水平之间的关系,其logistic模型为:
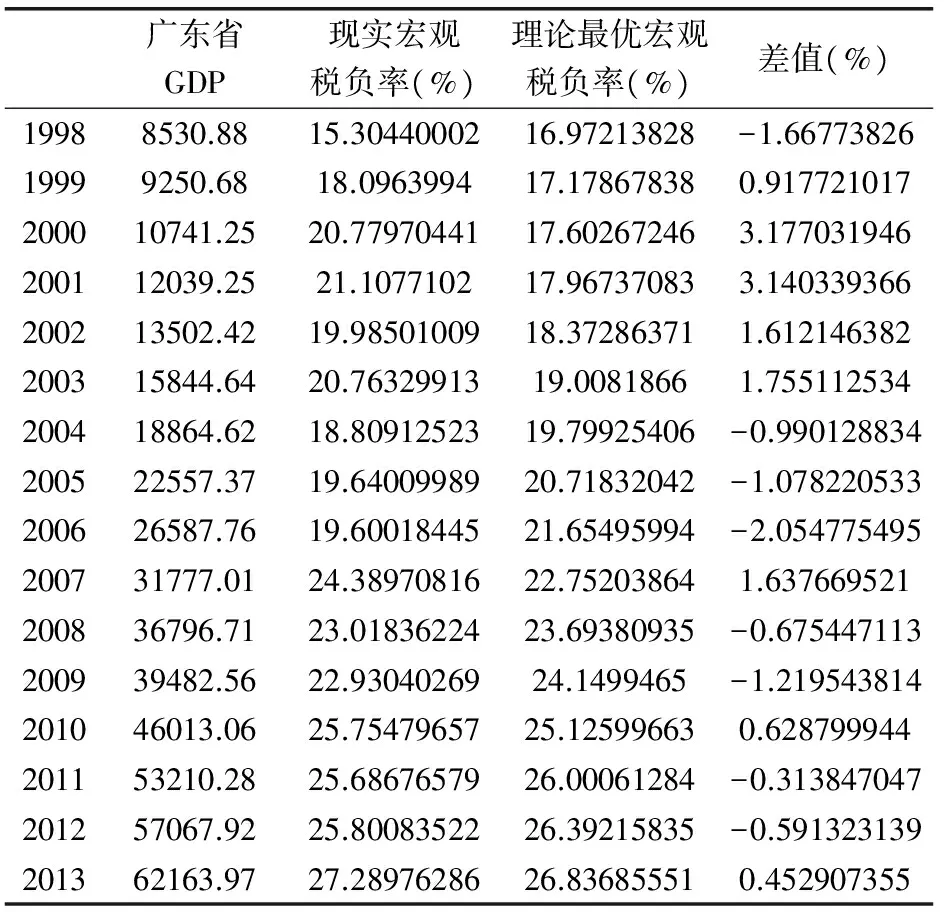
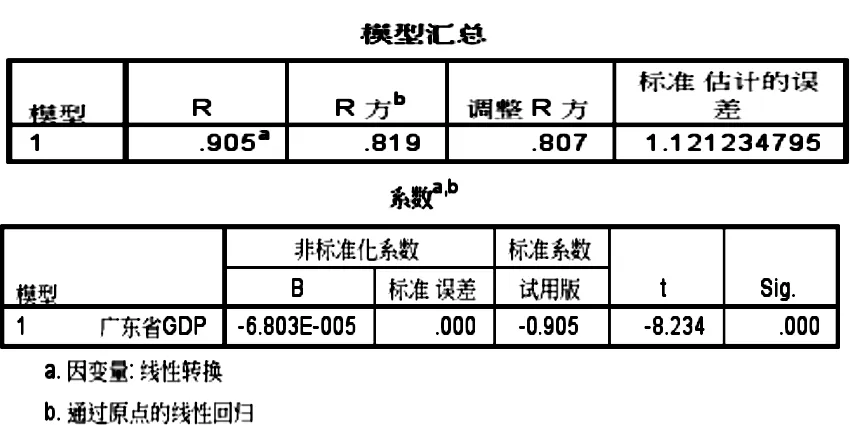
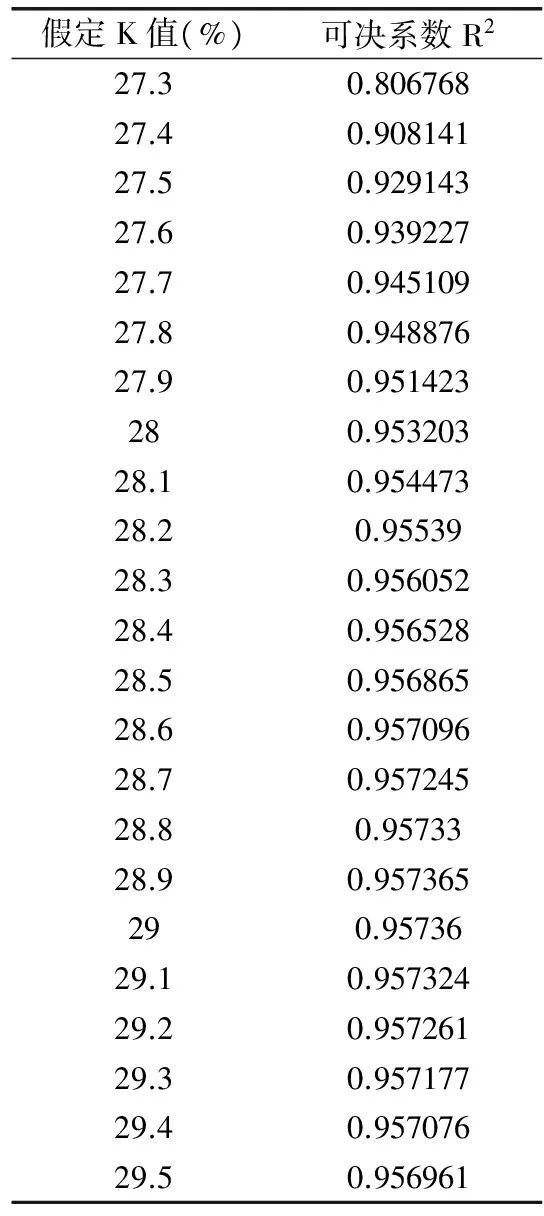
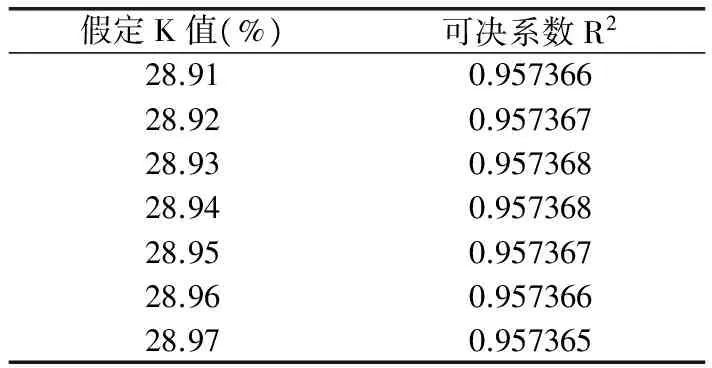
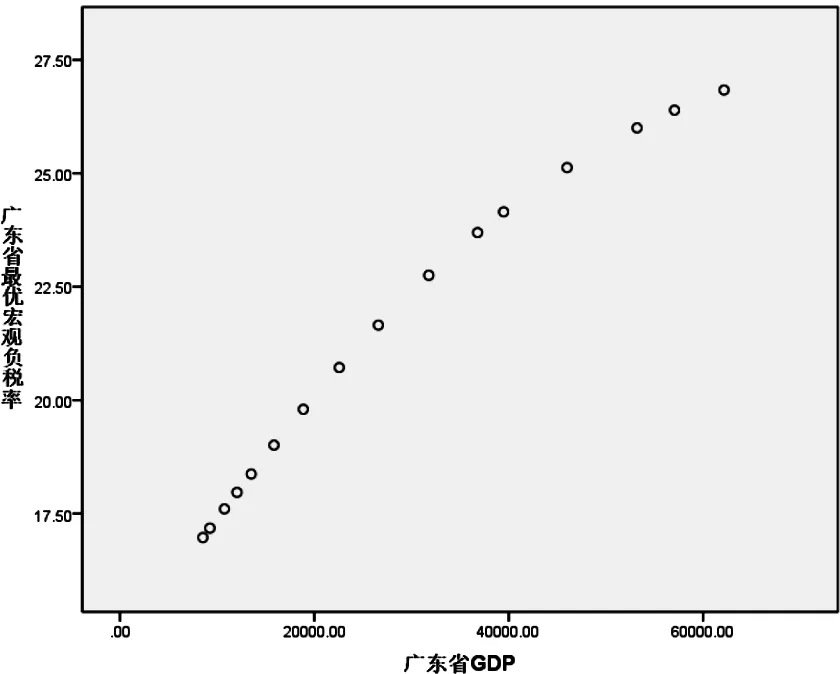
其中K为宏观税负率的极限值,范围是0 为了方便回归分析,先采用数学方法将曲线函数logistic转换为线性函数,如下式: 为了分析广东省财政收入的合理性,首先我们要找到符合广东省实际情况的logistic函数,即找出广东省的最优宏观税负率K和参数b0、b1的值。本文使用的方法具体步骤如下: 第一步,根据广东省宏观税负率的数据,找出最大值。根据这个最大值,估计一个稍大于它的极限宏观税负率记为K,然后将广东省GDP和宏观税负率带入到线性的logistic函数中进行回归分析,记录得出的b0、b1和可决系数R2。 第二步,将K增加0.1%,重复第一步的步骤,记录下此时的b0、b1、R2。不断以每次增加0.1%的速度改变K的值,并且记录下每次回归后的b0、b1、R2。比较可决系数R2,直到R2出现了先增后减的规律后才停止该步骤。 第三步,观察R2,选出以最大的R2为中点的一个长度为0.2%的区间。然后从最小的K值开始以每次增加0.01%的速度进行回归分析,过程类似于第二步,记录下每次的b0、b1、R2值,知道R2出现了先增后减的规律后才停止该步骤。 第四步,观察R2,选择出R2最大的那组b0、b1。至此便可以得出由广东省GDP和广东省最优宏观税负率的logistic表达式。 从1998年到2013年的数据(表2)中我们可以发现广东省宏观税负率随着GDP的增加也在不断上升。最大值为2013年的27.28976286%,于是我们不妨假设K的初始值为27.3%。当K为27.3%时有: 图3 K=27.3%时回归结果 特别需要解释的是,当包含常数项b0的归回结果不满足b0的显著性概率要远小于0.01的要求时,则选择通过原点的线性回归。之后的回归遇到相同情况时,都用这种处理办法。回归结果如上图所示。记录下b0、b1、R2后,按照上文所说步骤逐步找出广东省的宏观税负率极限值,结果如表3。 表3 K值和可决系数R2的关系 当K=28.9%时,R2最大,为了进一步得出更加准确的R2,选取28.8%到29%这个区间,以0.01%为精度进行进一步回归,结果如表4所示。 表4 当K=28.8%~29%时量和回归结果 图4 广东省最优宏观负税率图 观察可得广东省的宏观税负极限值应该为28.93%或28.94%,本文选取28.935%为最终的广东省宏观税负率极限值。其具体回归结果为:R2=0.975368,b0=0,b1=-0.000041。即广东省最优宏观税负率(记为T)和广东省GDP(记为X)的函数关系式为: 转换为logistic函数则为: 3.3 基于Compertz曲线回归分析 姚绍学博士在其论文中使用的Compertz曲线的函数表达式为: T=KABx·ε 其中,T表示宏观税负率(%),K表示宏观税负率的极限值,满足T<100%。x为广东省GDP,A,B为待估计参数,ε为随机误差项。 拟合过程和Logistic类似:取K初始值为27.3,进行回归拟合;然后增大K值,增加幅度为每次0.05,记录拟合优度R2、显著水平、A和B的估计值以及它们的t检验值和显著水平。重复以上步骤,最后比较拟合优度和t值,找出最优的A、B估计值,并记录下来。得出的最优拟合结果如表5所示。 表5 Compertz函数回归结果 对该估计结果进行双样本t值检验,得出差值估计值为0.214。检验结果显示,实测结果与计算结果在95%置信度上无差异。因此我们得出广东省最优宏观税负率(记为T)和广东省GDP(记为X)的Compertz函数关系式为: T=39.78×0.450.99x 因此,原理上我们可以基于广东省每一年的GDP实际情况,通过Logistic函数,计算出最优的宏观税负率。并且把理论上的最优宏观税负率与实际值进行比较,得出广东省近年来的宏观税负率是否合理。计算结果如表6所示。 表6 广东省每年GDP的宏观税负率及差值 从表中我们可以看出,近年来现实的宏观税负率与最优宏观税负率之间的大小关系并不确定。比如,2010年广东省宏观税负率大于最优宏观税负率,财政收入偏大。但是2011年和2012年的宏观负税率又要小于最优宏观税负率。分别小了0.312%和0.591%。到了2013年,情况又再次发生了变化,现实的宏观税负率大于了理论最优宏观税负率,大于的程度为0.453%。 但是总体来说,我们可以发现,现实的宏观税负率不会偏离理论上的最优宏观税负率太远,近年来的偏差值都要小于1%。偏离的幅度要远远小于2000年的3.18%和2001年的3.14%。因此我们可以这要认为广东省近年来的宏观税负率在合理水平,趋近与最优宏观税负率,财政收入的总量合理,既能满足政府实现其职能的需要,又不会阻碍经济的发展。 [1] 李健.我国财政收入适度规模的基本分析[D].大连:东北财经大学,2011. [2] 刘锐.适度财政收入研究[D].太原:山西财经大学,2011. [3] 姚绍学.最优财政收入规模理论与实证[D].天津:天津大学,2002. [4] 寻子员.拉弗曲线理论分析及其启示[J].山东财政学院学报,2003. [5] 姚绍学.最优财政收入规模问题研究评析[J].经济研究参考,2002. [6] 李秀艳.广东省适度财政收入规模的研究[D].广州:广东外语外贸大学,2013. [7] 洪梅华.我国财政收入适度规模问题研究[D].苏州:苏州大学,2005.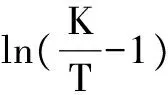

4 运用Logistic函数判断广东省财政收入的合理性