城镇化对经济增长影响机制研究——以武汉市为例

李 昊

(武汉大学中国中部发展研究院,湖北 武汉430072)

1 问题的提出

城镇化是指人口和产业活动在空间上集聚、乡村地区转变为城市地区的过程,它是一种在空间体系下的经济转换过程。由于规模经济和集聚经济效应,经济和人口慢慢集中于城市。一方面,经济增长最终结果使得城市出现聚集、城市规模扩大从而城镇化水平提高,另一方面,城镇率的提升对经济增长也有着明显的影响作用。

国外有关城镇化对经济增长影响的实证研究可以追溯到上世纪中期。最初由美国经济学家兰帕德(E.E.lampard)通过对美国相关经济数据研究发现,美国城市发展水平与经济增长之间呈现一种非常显著的正相关关系,将经济发展程度与城镇化阶段进行划分,发现两者有着明显的对应关系。1965年,美国地理学家贝里做了类似的研究,通过选取并对比分析全球中95个国家的资料,他同样发现城镇化与经济水平之间有着一定的正相关关系。Renaud(1981)进一步扩大了研究对象,选取了111个国家进行分析,结果仍显示一国经济水平与成长率之间密不可分;H.钱纳里(1988)通过采用1950至1970二十年间101个国家的相关经济数据对经济发展状况与城镇化率进行相关性分析,论证了在一定的人均GNP范围内,生产结构、劳动力配置与城镇化率三者之间存在着一一对应的关系。Moomaw和Shatter(1996)通过回归分析,发现城镇化率与人均GDP、工业化程度、出口及外国援助之间呈正相关关系,而与农业生产水平之间则呈现出反向关系。McCoskey和Kao(1998)选取了30个发展中国家及22个发达国家的面板数据作为样本,利用动态计量方法分析了城镇化与人均产出、人均资本之间的关系,得出它们存在着某种长期均衡关系的结论。Bertinelli和Strobl(2003)采集了1960～1990间39个国家的面板数据为样本,利用半参数方法进行估计,发现经济增长与城市聚集之间呈现出U形曲线的特性。

国内对城镇化领域的研究则相对较晚,但通过大量的实证研究分析,同样发现城镇化与经济发展水平之间存在显著的正相关关系。周一星(1995)选取了1977年间全球157个国家及地区的资料研究分析,通过计算分析得出二者之间相关系数为0.9079,呈现出十分明显的对数曲线关系。1988年许学强根据美国人口普查局公布的1981年151个国家的资料,绘制散点图并选配对数曲线,发现城镇化水平与人均GNP之间同样存在着对数曲线相关,相关系数为0.81;成德宁(2004)根据世界银行公布的2002年76个国家人均GNP和城镇化率的资料,拟合对数曲线模型,得出了与周一星一样的结论。张宏霖(2003)则对国内的经济情况进行了评估,他利用我国各省1978年、1998年的城镇化水平及人均GDP数据,证明了在我国城镇化率与经济发展水平之间同样也是正相关关系。

由此我们不难发现,城镇化与经济增长在宏观层面上确实存在着明显的协同增长作用,也就是说,普遍来看,城镇化水平较高的国家或地区其工业化程度和经济发展水平也较高。

但同时我们需要留意的是,城镇化并不像资本劳动力等生产要素一样直接作用于经济增长,它是通过某种特定的途径间接地对经济增长产生影响,而这种影响机制则决定了城镇化对经济发展的影响力的大小。根据Henderson在2002年的研究发现:我们无法确定城镇化程度和经济增长有直接的关系。那么,城镇化的加深具体是如何作用到经济增长的?这一种作用方式的影响程度究竟有多大?其在中国的作用效率又是如何?这种影响是否能对中国目前的城镇化与经济发展起到理论指导作用?本文将通过对处于中部地区的武汉市近18年的数据进行实证分析,以确定在当前中国经济环境下这种影响机制的作用情况。

2 计量模型的设定、数据来源和计量方法的选择

2.1 计量模型的设定

本文模型基础选用柯布—道格拉斯生产函数:

其中Y代表产出,K表示物质资本存量,H为人力资本存量,α∈[0,1],A常表示知识,在这里为技术、制度等,并且在该函数中物质资本和人力资本皆为规模报酬不变变量。

除去资本、技术因素,作者认为产业升级也是城镇化促进经济增长的作用路径,具体来说,城镇化的加深能提高国民经济中二、三产业的比重,而根据结构主义学派理论,结构变革能够加速经济增长,因此本文在模型设定中添加产业结构为解释变量。

根据上文的分析设定,本文建立如下计量模型:

即:总产出Y是物质资本K、人力资本H、产业结构STR以及A中的制度、技术、文化、结构等其他因素的函数。将式(2)变形为人均形式,并对等式两边取自然对数得到函数等式:

其中人均产出y＝Y/L,人均物质资本k＝K/L,人均人力资本h＝H/L,t为时间下标,c0是常数项,μt是随机干扰项,表示受随机因素影响而未被模型采用的偶然因素。c1、c2、c3分别表示lnkt、lnht、STR的变化对GDP增长的作用程度。

详细释义如下,lny:历年人均地区生产总值自然对数值,用于表示经济增长速度。lnk:历年人均物资资本自然对数值。从理论分析上看,该变量应该和人均产出正相关,也就是说物质资本对经济增长具有正面影响。考虑到数据的可获得性和合理性,本文用人均固定资产投资代替。lnh:历年人均人力资本的自然对数值。根据多数文献中应用的方法,本文采用高校在校学生人口来代表人力资本。STR:产业结构因素,目前常用二、三产业占地区总产值比重表示,用来测度产业结构高级化的程度,根据结构主义学派理论,我们测断该指标与人均产出正相关。除此之外模型不再考虑文化、制度等其他因素的影响。即使有影响,其影响会在残差项中综合体现出来。

进一步,为确定城镇化改进经济增长的作用路径,我们设定以下计量模型:

上述模型方程组中,是往年城镇化水平,由于没有统一的指标表示该变量,在这里我们用城镇人口比重来代替。而通过之前的论证可得,物质资本、人力资本以及产业结构这三个变量皆与城镇化水平之间有着正相关关系。

2.2 数据来源和计量方法的选择

本文的数据主要来源于湖北省统计局网站和中国城市统计年鉴1995－2012(电子版)。关于计量论证方法,我们选择的是国内学术界普遍认可运用的方法,即选取简单的时间序列或某一特定时点的截面数据,利用最小二乘法进行回归预算,从而估计确定各变量的系数。

3 计量分析及其结果

本文分析思路步骤如下:第一步从整体上确定城镇化与经济增长两者的关系,是否相互有影响,然后对(3)－(7)式进行估计,以确定哪些因素对人均产出有显著影响,进一步分析其在推动经济增长过程中起到的作用,最后详细分析并阐述检验结果。

首先探究城镇化对人均产出作用效果,我们在这里利用调整后的人均国民生产总值对数(下文亦采用此值)对城镇化率 进行回归,运算结果如表1。

表1 经济增长与城镇化关系的总体分析

回归函数为:LNY ＝ －3.33847470282＋0.218707161246∗URB。

从表1可以看出,城镇化的系数为0.218707,经调整后的拟合优度R为0.956167,这表明两者正相关且显著,与前文的分析预期一致。但是,分析到此处我们仍无法确定两者相互关联作用的机制是什么,下一步本文将逐步分析影响人均产出的相关因素。

本文通过对各变量的截取数据的分析,进而估测出对人均产出的可能影响因素,同时对各个变量进行显著性检验,在此基础上来确定回归方程。对lnk、lnh和STR进行回归分析得出调整后的拟合优度R2依次为0.955735、0.922110 和0.913629,且各变量均通过显著性检验。

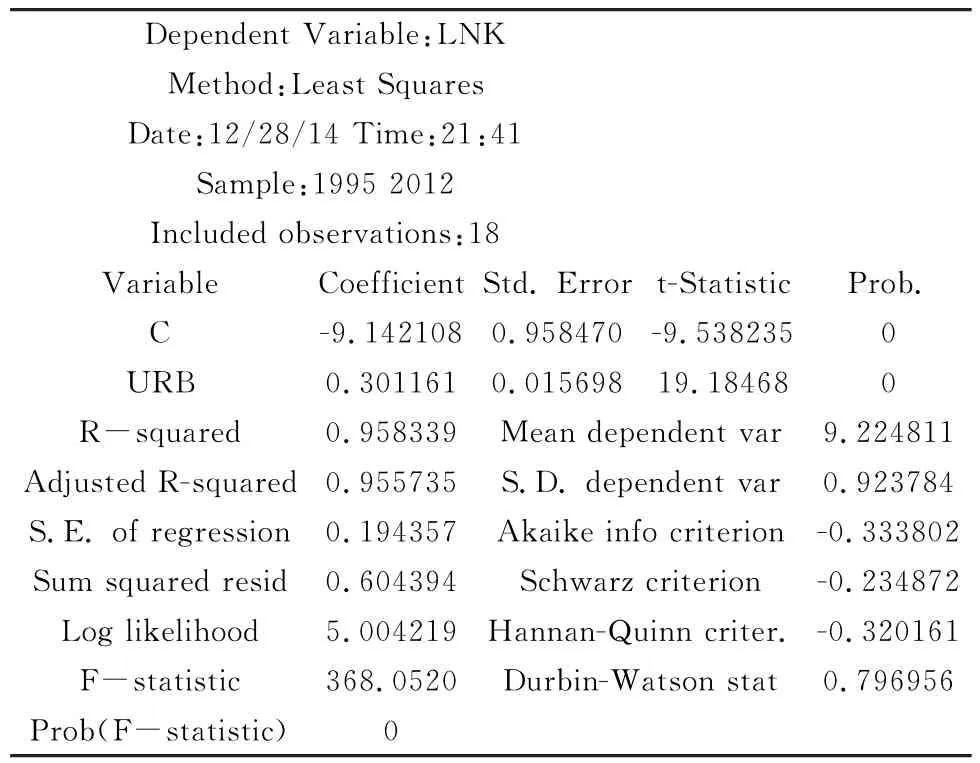
表2 人均物质资本与城镇化关系的分析

回归函数为:LNK ＝ －9.14210774164＋0.301160632789∗URB。

表3 人均人力资本与城镇化关系的分析

(续表3)

回归函数为:LNH ＝ －15.878489071＋0.211285767255∗URB。

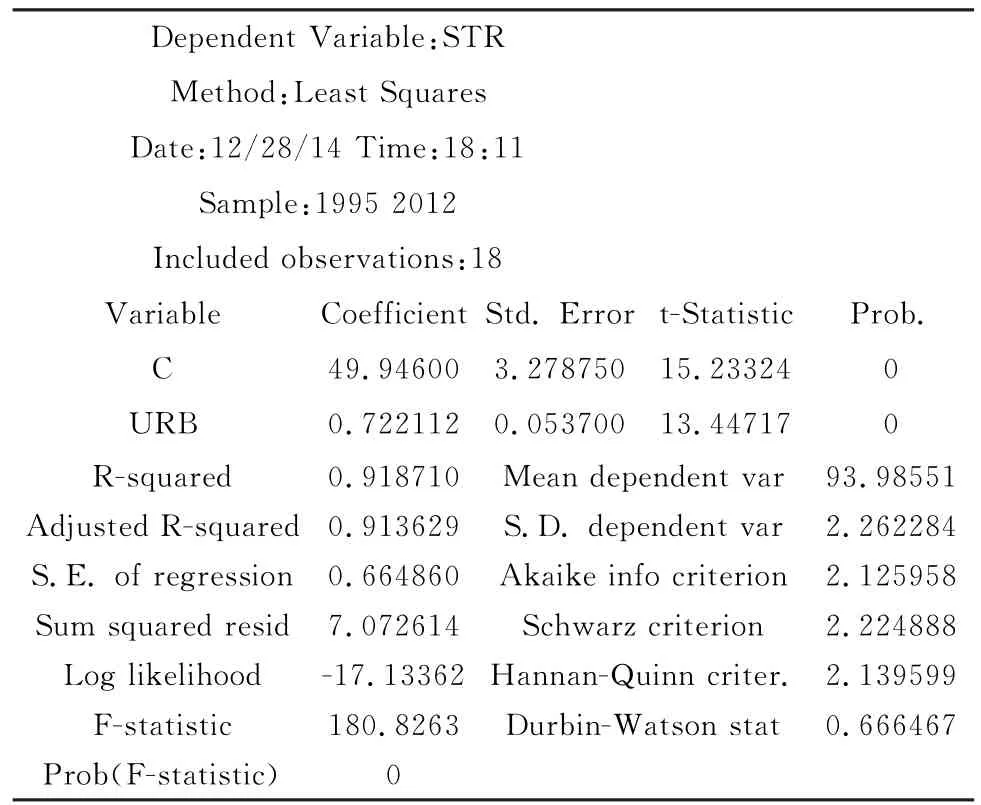
表4 产业结构与城镇化关系的分析

回归函数为:STR ＝ 49.9459962712 ＋0.72211180755∗URB。

下面对变量lnk、lnh和STR进行线性回归,进一步研究城镇化是如何影响经济增长的。

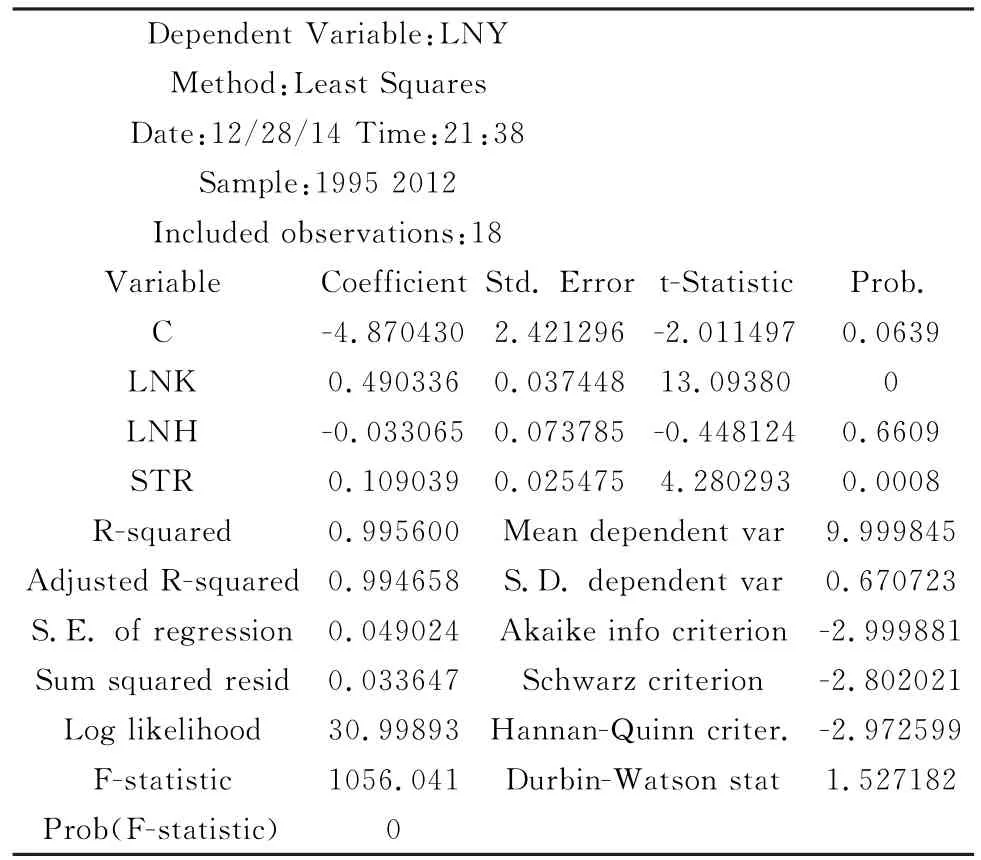
表5 城镇化对经济增长的影响机制分析

回归函数为:LNY ＝ －4.87042981084＋0.490335550338∗LNK －0.0330647964098∗LNH＋0.109038781962∗STR。

4 检验

4.1 经济意义的检验

该模型具有良好的经济意义,能通过初步检验,各参数的符号及含义符合经济理论,但是这里的LNH的系数为负值,表明人均人力资本与经济增长呈反向相关关系,我们在多重共线性里再进行分析。

4.2 统计检验

由运算结果可知R2值为0.9956,校正后的R2值为0.994658,表明模型的拟合状况较好。运行F检验得出其值为1056.041,表明对该模型而言储蓄率的增长影响具有明显的显著性。

4.3 计量经济检验

4.3.1 多重共线性的检验

从上文的检验结果可知该模型整体上具有较强的显著性,但是我们单独对各个变量进行分析后发现C、LNH不显著,存在多重共线性的可能,通过逐步回归方法尝试消除多重共线性发现我们需放弃常数项C。此时再次做回归分析结果如表6。

表6 回归分析结果

从新模型的回归结果来看,R值处于良好的范围,同时各个变量的t统计量也显示出了较好的显著性。所以回归函数为:LNY＝0.519389751015∗LNK＋0.0985652831342∗LNH ＋0.0585586766077∗STR。

4.3.2 异方差性检验

接下来对新模型进行异方差性的检验,通过white检验得出结果如表7。

表7 异方差性的检验结果

我们可以看到Obs∗R－squared的运算结果为4.404638,在运行过程中我们并没有采用交叉乘积项的方式,所以设定自由度为6,在显著水平为0.05的情况下,查表得(6)＝12.59＞4.404638,拒绝原假设,因此认定该模型不存在异方差性。

4.3.3 自相关性的检验

从表6我们可以看到DW值为1.466004,且样本容量n＝18,在存在三个解释变量的条件下,我们给定显著性水平＝0.01,查 D—W 表得,d＝0.882,d＝1.407,这时有d＜dw＝1.466004＜4－d,表明不存在一阶自相关(这里我们仅检验一阶自相关性)。

5 结论及政策建议

经过以上计量模型的处理,通过对武汉市的实证分析,我们可以看出,城镇化对经济增长的影响作用主要通过物质资本、人力资本、知识资本以及产业结构这四个渠道产生,μt表示未被我们考虑在内的因素。进一步,对时间序列数据的回归分析可以论证,城镇化对于人均产出的作用通过人力资本、物质资本和产业结构改善三种方式产生,同时需要指出的是,虽然人力资本在1.9%的显著水平通过检验,但其作用效果仍然不是很显著,除此之外的其他因素则由于影响较弱皆可忽略不计。

一方面,通过总体分析我们可以确定城镇化与人均产出之间的显著正相关,这说明城镇化水平的提高确实在一定程度和意义上促进了经济的增长。进一步,通过对人均产出决定因素的回归我们可以确定,物质资本、人力资本和产业结构这三个因素在对中国的人均产出影响中起着主要作用,其中物质资本的作用力最大,是推动武汉市经济增长的首要因素,人力资本为第二位影响因子。产业结构则通过间接影响排至三位,具体表现为第二、三产业的高速增长和比重的加大也能够在一定程度上推动经济前行。而其它未被我们考虑在内的相关因素则由于影响力较弱,基本可以忽略不计。由此可见,城镇化对经济增长的作用途径主要是通过以上三个方面实现的。

通过以上的理论及实证分析,本文对武汉的政策建议如下:一方面,由于资本是作用于经济发展的主要因素,应进一步加大武汉市的固定资产投资等生产要素的投入,同时在人力资源方面,武汉作为全国重要的教育基地和大学集聚地,要充分发挥科技和教育优势,依靠科技创新加快劳动者职业素质提升,通过提供相对优惠政策减少人才流失,累积改善人力资本数量和质量双管齐下,优化经济质量。另一方面,产业结构方面的影响也不能忽略,要加快武汉市产业结构优化升级。同时,随着城镇化的快速发展,不仅要加大对第二产业和第三产业的发展力度,在发展高新技术产业的同时也要逐步承接国际服务业转移,积极开展与周边国家和地区的产业承接和转移,将一些劳动密集型的工业制造业产业逐步转移到城市圈周围的其他合适地区。

[1]沈坤荣,蒋锐.中国城市化对经济增长影响机制的实证研究[J].统计研究,2007,24(6):9-15.

[2]杰弗里.M.伍德里奇.计量经济学导论(第四版)[M].北京:中国人民大学出版社,2010.

[3]周一星.城市地理学[M].北京:商务印书馆,1995.

[4]谭晴.基于Eviews我国城镇居民储蓄率变化实证分析[J].2009,(8):145.

[5]朱金平,傅兆君.城市化对经济增长的影响机制研究[J].

[6]张晓峒.Eviews使用指南与案例[M].北京:机械工业出版社,2007.