政府科技投入对医药企业研发投入影响分析

孟丽姣 李 勇

(中国药科大学国际医药商学院,江苏 南京211198)

研发投入是开展研发活动的基础,是反映一国自主创新能力的重要指标之一。而企业是研发活动的主体,也是研发投入的主要来源,但是新药研发活动具有不确定性和公共产品等特点,会抑制医药企业研发投入。因此,政府有必要制定相应的政策对医药企业研发活动进行适度干预,而政府科技投入是目前普遍采用的激励措施之一。

但政府科技投入是否真正促进医药企业研发?影响时滞为多久?影响贡献率为多大?这种影响是单向还是双向?为解决以上问题,本文将从研究综述、模型构建、实证检验及结果分析、建议四个方面展开讨论。

1 研究综述

关于政府科技投入对企业研发投入的影响,国内外学者均从不同角度做了很多研究,由于研究对象及研究方法的不同,并未得到一致结论。政府科技投入对企业研发投入可能会产生两种影响:

一为杠杆效应,即政府科技投入能促进企业研发投入的增加。王霞等(2014)通过对1480家上海新兴产业中的民营企业进行分析,发现政府科技投入对企业研发投入的杠杆作用要强于挤出作用,且两者存在长期均衡关系。寇铁军,马大勇(2013)分析了1991年－2011年间政府科技投入与企业研发投入之间的关系,发现我国政府科技投入对技术创新投入引导效应弹性系数为0.7014,且政府科技投入是企业研发投入的Granger原因。Benjamin Montmartin等(2015)利用1990－2009年间25个0ECD国家的数据,研究发现政府研发补贴与财政激励政策在一个国家内将对私人研发有积极的空间溢出效应。Sergio Afcha(2014)与Massimo G.Colombo(2011)亦得出相同结论。

二为挤出效应,即政府科技投入会导致企业研发投入减少。苏盛安,赵付民(2005)采用广义矩阵法从宏观层次上得出结论政府直接资助对企业的科技投入产生挤出效应。孙燕,孙利华(2011)构建多元线性回归模型亦得出相同结论。

已有研究有许多值得借鉴之处,但也存在不足:(1)关于指标的选取:已有研究中要么以“企业自筹的研发投入”为考察指标,要么以“企业研发经费支出”为考察指标,无法全面准确的说明政府科技投入对企业研发投入的影响情况。(2)关于相互影响关系:现有的研究中只关注了政府科技投入对企业研发投入的单向影响,而政府科技投入对企业研发投入是一个动态的长期的过程,政府与企业作为企业研发的重要主体,其中一方的变化都可能影响到另一方的改变,所以有必要对两者之间的相互关系进行分析。(3)关于滞后期的确定:研发投入是具有滞后性的,滞后期不同,所得出的结果也会不同,已有文献中大多主观设定滞后期,使研究结果缺乏科学性与准确性。(4)关于内生性的处理:政府科技投入在对企业产生影响时,可能会受到各种因素影响,如企业规模、企业性质等,分析时无法把所有因素都涵盖其中,于是产生内生性问题。目前大部分研究所采用的回归方法并不能消除内生性。

针对以上问题,本文将采用我国26个省市医药制造业1999－2013年的面板数据,通过建立PVAR模型,从企业自筹研发投入与企业总研发投入两个方面综合分析政府科技投入与企业研发投入的相互影响关系,并进一步分析影响的动态变化及影响贡献率,以期对已有研究有所补充,对相关政策分析有所启示。

2 模型构建

PVAR模型由Holtz－Eakin首次提出,现已发展为一个兼具面板数据分析与时序分析优势的成熟模型;PVAR方程把所有变量看成一个内生系统来处理,可解决变量内生性问题;考察了所有变量的滞后项,能真实反映变量间的互动关系;还能分析系统变量间的冲击响应和方差分解。

本文将建立如下PVAR模型:

在式(1)中,yit是基于面板数据2×1的变量向量,其中:当研究政府科技投入与企业自筹研发投入的关系时,yit＝(ZFTRit,QYTRit)τ;当研究政府科技投入与企业总研发投入的关系时,yit＝(ZFTRit,QYZCit)τ。其中,ZFTR指政府科技投入,用企业科技活动经费筹集额中的政府资金这一指标来衡量,QYTR指企业自筹研发投入,用企业科技活动经费筹集额中的企业资金这一指标来衡量,QYZC指企业总研发投入,用企业研发经费内部支出这一指标来衡量。下标i(＝1,2,…,26)表示26个省市,t表示1999－2013年,λ为滞后阶数,Bλ是滞后λ期时变量的系数矩阵,αi是省效应向量,γt是年效应向量,μit是随机扰动项。

由于西藏、新疆、宁夏、青海、海南五省数据缺失被排除,本文选取了1999－2013年其余26个省市医药制造业的面板数据进行研究,所用到的数据全部来自《中国高技术产业统计年鉴》。

3 实证检验与结果分析

3.1 变量平稳性检验

3.1.1 单位根检验

数据平稳性对于时间序列的模型构建至关重要。如果数据不平稳,可能会导致两个相互独立的变量出现伪相关关系。单位根检验是检验数据平稳性最常用最精确的方式,其中,常用的单位根检验方法有LCC检验、ADF检验、Hadri检验等,由于检验原理不同,检验结果也不尽相同。本文将采用这三种方法同时进行检验,结果如表1所示。综合三种方法的结果,企业自筹研发投入、企业总研发投入、政府科技投入三者均通未过显著性检验,所以无法拒绝原假设,三个变量都是不平稳的;但是经过一阶差分后,虽然企业总研发投入与企业自筹研发投入的LCC检测值未通过显著性检验,但是ADF及Hadri检测值均通过了显著性检验,而政府科技投入的三个检测值均通过了显著性检验,所以认为这三个变量的一阶差分均是平稳序列,即皆为一阶单整变量。

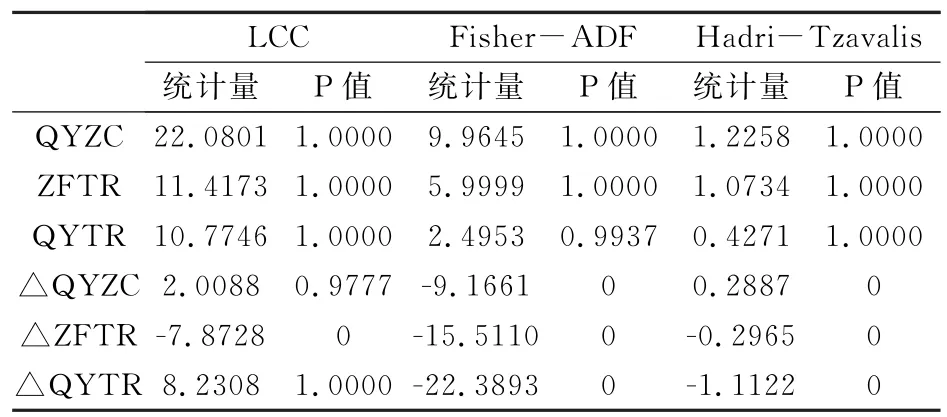
表1 单位根检验

3.1.2 协整检验

本文接着进行面板协整检验,协整的思想就是把同阶非平稳变量放在一起进行分析,通过这些变量进行线性组合,从而消除它们的随机趋势,得到其长期联动趋势。结果如表2所示,虽然Gt值(Group－T检验)没有通过显著性检验,但是Ga(Group－ADF检验)、Pt(Panel－T检验)、Pa(Panel－ADF检验)值均在1%显著性水平显著,所以企业自筹研发投入、企业总研发投入、政府科技投入虽然是不平稳序列,但是彼此之间通过形成线性组合后,将存在长期均衡关系。

表2 协整检验结果

3.2 确定变量最优滞后阶数

本文分别对数据做了一至五阶滞后的模型估计,综合考虑AIC准则(赤池信息准则)、BIC准则(贝叶斯信息准则)、HQIC准则(滞后阶数确定准则),从而得出最优滞后阶数。结果如表3所示,企业自筹研发投入与政府科技投入的最优滞后阶数为一阶,企业总研发投入与政府科技投入的最优滞后阶数为三阶。

表3 滞后阶数估计

3.3 PVAR模型实证检验

3.3.1 PVAR模型的处理过程

首先本文采取前向均值差分(Helmet)消除了模型的固定效应,并保证滞后变量与转换后的变量正交,而与误差项无关,可作为GMM估计的工具变量。GMM方法可得出变量自身的滞后和其余变量的滞后对该变量的短期影响,结果如表4、表5所示。

表4 QYTR与ZFTR的GMM估计结果

表5 方差分解结果

随后,本文进行了脉冲响应分析,即在其他变量保持不变的情况下,给一个变量的扰动项加入一个标准差的冲击,研究其如何对模型中其他变量产生动态影响。脉冲响应函数是通过PVAR参数构造的,必须考虑标准差,但是标准差难以通过计算得到,因此本文通过蒙特卡洛方法模拟产生置信区间。结果如图1、图2所示。

为了更清楚地刻画各变量之间的相互影响程度,本文进一步采用方差分解的方法,分析每个随机扰动对PVAR模型中的变量产生影响的贡献度。表6、表7给出了第10个预测期、第20个预测期和第30个预测期的方差分解结果。

3.3.2 PVAR模型的结果

(1)政府科技投入与企业自筹研发投入的影响。

政府科技投入与企业自筹研发投入的GMM估计结果如表4所示。把企业自筹研发投入作为依赖变量时:滞后一期的企业自筹研发投入对当期企业自筹研发投入的影响系数为－0.044,但是P值为0.609,所以影响并不显著;滞后一期的政府科技投入对当期企业自筹研发投入的影响系数为13.67,且非常显著。

把政府科技投入作为依赖变量时:滞后一期的政府科技投入对当期政府科技投入的影响系数为0.774,且很显著;而滞后一期的企业自筹研发投入对政府科技投入的影响系数为0.005,P值为0.189,影响不显著。

脉冲响应结果如图1所示。在当期给政府科技投入一个标准差大小的正冲击后,企业自筹研发投入在第一年迅速增加,第二年开始增加力度逐年减小,但在未来五年影响皆为正。

在当期给企业自筹研发投入一个标准差大小的正冲击后,政府科技投入在第一年有极小程度的增加,第二年开始以平缓的速度减少。

图1 ZFTR与QYTR的脉冲响应函数图

由表5可知,经过20个预测期之后,系统已基本稳定。其中,企业自筹研发投入的变化来自于政府科技投入波动的影响程度约为43.33%;而政府科技投入的变化来自于企业自筹研发投入波动的影响程度仅为1.67%。

综上:政府科技投入与企业自筹研发投入具有单向影响关系。其中:一方面,滞后一期的政府科技投入对企业自筹研发投入有显著的正向影响,当期政府科技投入增加后,对企业自筹研发投入接下来的一年中影响程度最大,随后效果会逐渐减弱,且政府科技投入对企业研自筹发投入的波动贡献度高达43.33%。另一方面,企业自筹研发投入对政府科技投入并无显著的影响。

医药企业中一些风险高、外部效用大的项目,如新药基础研究,企业不愿也无法承担风险,而政府的科技投入能降低企业创新投入的风险,增加企业研发成功的概率,从而激励企业增加自身的研发投入。而企业自筹研发投入只是企业总研发投入中的一部分,企业加大自筹研发投入后,企业的总研发支出及研发产出并不一定是增加的,所以政府并不会因为企业自筹研发投入的变化而去改变科技投入政策。

(2)政府科技投入与企业总研发投入的影响。

政府科技投入与企业总研发投入的GMM估计结果如表6所示,把企业总研发投入作为依赖变量时:滞后一期的企业总研发投入对当期企业总研发投入有正向影响,滞后二期、三期的企业总研发投入对当期企业总研发投入有负向影响,但是均不显著;滞后一期、二期、三期的政府科技投入均对当期企业总研发投入产生正向影响,但是只有滞后一期时显著。

把政府科技投入作为依赖变量时:滞后一期、二期、三期的政府科技投入对当期政府科技投入产生正向影响;滞后一期的企业总研发投入对当期政府科技投入产生正向影响,但是并不显著,滞后二期、三期的企业总研发投入对当期政府科技投入产生负向影响,但是只有滞后二期时才显著。

表6 QYZC与ZFTR的GMM估计结果

政府科技投入与企业总研发投入的脉冲响应函数如图2所示,在当期给政府科技投入一个标准差大小的正冲击后,企业总研发投入在第一年迅速增加,第二年后仍以极平缓的速度在增加,至第三年达到最大值,第四年后逐渐减小,未来五年的影响皆为正。

在当期给企业总研发投入一个标准差大小的正冲击后,政府科技投入在第一年有极小程度的增加,第二年会迅速减少,第二年后以平缓的速度减少。

图2 ZFTR与QYZC脉冲响应函数图

政府科技投入与企业总研发投入的方差分解结构如表5所示。经过20个预测期之后,系统已基本稳定。企业总研发投入的变化有65.39%来自于政府科技投入的变化。而政府科技投入的变化只有23.54%来自于企业总研发投入的变化。

综上:政府科技投入与企业总研发投入具有双向影响关系。其中:滞后一期的政府科技投入对企业总研发投入产生显著正向影响;当期政府科技投入增加后,企业总研发投入在接下来的一年迅速增加,第二年后仍以极平缓的速度在增加,至第三年达到最大值,第四年后逐渐减小;企业总研发投入的变化有65.39%来自于政府科技投入变化。滞后二期的企业总研发投入对政府科技投入产生负向影响;当期企业总研发投入增加后,政府科技投入在第一年有极小程度的增加,随后开始减少;政府科技投入的变化只有23.54%来自于企业总研发投入的变化。

政府科技投入一方面可降低研发风险、提高研发效率,从而改变企业的研发决策行为,另一方面通过改变企业投资研发的成本结构、增加融资渠道等方式来缓解企业的融资约束,从而促使企业的总研发投入随之增加。Miguel Meuleman等(2012)研究发现获得政府补贴将能提供一个关于中小企业质量的积极信号,从而利于企业获得长期债务融资。Massimo G.Colombo等(2013)则从微观角度分析了1994－2008年288个意大利NTBFs企业的数据,发现获得政府补贴的NTBFs企业会增加投资和降低投资现金流的敏感性,融资约束得到缓解。而政府对企业进行科技投入的目的在于缓解企业研发的融资约束,激励企业加大总研发投入,当企业逐步加大总研发投入后,政府科技投入的目的已达到,将会对其减少科技投入。

4 建议

政府科技投入对企业自筹研发投入及企业总研发投入均产生杠杆效应,所以政府科技投入对促进医药企业技术创新是有效且必要的,一方面,政府需继续适度的加大对医药企业的直接科技投入,另一方面,可借助间接手段促进医药企业新药研发,包括:(1)对医药企业提供政府融资担保,降低医药企业融资成本;(2)通过逐步扩大医疗保险覆盖范围等政府采购政策,扩大医药产品的市场需求;(3)通过对研发机构及高校的公共投资,促进基础研究的提升,从而降低医药企业研发的技术成本。

政府科技投入对医药企业总研发投入具有双向影响关系影响,所以无论于政府还是于企业,投入都存在一定的限度。对政府而言,进行科技投入的目的是为了引导和激励企业研发投入,若过分投入则会挤出企业研发投入,既违背了初衷也是无效政策。对企业而言,技术创新是企业发展的源泉,一旦研发成功会给企业带来莫大效益,但是,高收益背后隐藏着高风险,一旦研发失败会给企业带来灭顶之灾,所以企业面对研发是谨慎的。只有平衡好政府与企业在研发投入中的份额比例,平衡好企业内部融资与外部融资在技术创新中的功能分配,才能使政府与企业最好的发挥各自的作用,才能使技术创新效果达到最优,从而使企业经济效益与社会效益最大化。

[1]王霞,顾琪虹,郭兵等.政府R&D资助对企业R&D投入的作用——基于2008—2012年上海1480家民营企业数据的实证分析[J].技术经济,2014,(4).

[2]寇铁军,马大勇.我国政府科技投入对企业研发投入引导效应的实证分析[J].地方财政研究,2013,(10).

[3]Benjamin Montmartin.Marcos Herrera.Internal and external effects of R&D subsidies and fiscal incentives:Empirical evidence using spatial dynamic panel models[J].Research Policy,2015,44(5).

[4]ergio Afcha.Guillen Leon Lopez.Public funding of R&D and its effect on the composition of business R&D expebditure[J].BRQ Business Research Quarterly,2014,(1).

[5]Massimo G.Colombo.Luca Grilli.Samuele Murtinu.R&D subsidies and performance of high－tech start－ups[J].Economics Letters,2011,(1).

[6]苏盛安,赵付民.政府科技投入政策工具对我国大中型工业企业科技投入的影响[J].科技管理研究,2005,(8).

[7]孙燕,孙利华.我国政府医药科技投入对企业研发支出影响的实证分析[J].中国药房,2011,(9).

[8]朱平芳,徐伟民.政府的科技激励政策对大中型工业企业R&D投入及其专利支出的影响[J].经济研究,2003,(6).

[9]陈钰芬,李金昌.政府R&D资助对企业R&D经费投入的影响——基于浙江省规模以上工业企业行业面板数据的实证分析[J].商业经济与管理,2011,(2).

[10]张瑞,苏方林,李臣.基于PVAR模型的R&D投入与产出关系的实证研究[J].科学学与科学技术管理,2011,(12).

[11]俞立平.不同科研经费投入与产出互动关系的实证研究——基于面板数据及面板VAR模型的估计[J].科研管理,2013,(10).

[12]Miguel Meuleman.Wouter De Maeseneire.Do R&D subsidies affect SMEs’access to external financing?[J].Research Policy,2012,(3).

[13]Massimo G.Colombo.Annalisa Croce.Massimiliano Guerini.The effect of public subsidies on firm’investment－cash flow sensitivity:Transientor persistent?[J].Research Policy,2013,(9).