基于模糊时间知识推理的高速铁路列车运行图冲突预测

庄河，冯丽萍Shool of Trnsporttion nd Logistis Southwest Jiotong University Chengdu 610031 Chin*，文超，彭其渊Ntionl United Engineering Lortory of Integrted nd Intelligent Trnsporttion Southwest Jiotong University Chengdu 610031 Chin，汤奇志Chin Rilwy Corportion Beijing 100844 Chin

基于模糊时间知识推理的高速铁路列车运行图冲突预测

庄河a,b，冯丽萍aSchool of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China,*，文超a,d，彭其渊a,cNational United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China，汤奇志bChina Railway Corporation, Beijing 100844, China

a r t i c l e i n f o

Article history:

Received 5 May 2016

Revised form 19 August 2016

Accepted 13 September 2016

Available online 21 September 2016

高速铁路

列车在运行过程中，由于受到系统内外的干扰，容易发生晚点并偏离计划列车运行线，而晚点传播将进一步扩大运行干扰的影响，造成后续列车潜在的运行冲突，这些冲突可能影响后续列车运行计划的安排。因此，可靠的冲突预测结果能够更好地辅助当前运行调整策略的制定，提高运行图实施效果。相比于既有研究中基于随机干扰的冲突预测方法，本文基于历史运营数据对计划列车运行图中的时间区间进行模糊化处理，并基于赋时Petri网建立高速铁路列车运行图模型。为了全面度量冲突预测结果，本文将冲突划分为确定冲突和潜在冲突并给出判定标准。同时提出了单列车运行线平均偏离度和相邻列车作业间的冲突可能性两个冲突评价指标，并给出了计算方法。基于调整后的模糊时间知识推理算法，本文提出了一种新的高速铁路列车运行冲突预测方法，应用于两个不同情境下的仿真算例中。仿真算例结果表明，列车运行图内时间区间模糊化处理后的冲突预测在可靠性和可操作性方面更强，并可为列车运行图调整、优化等提供决策支持。

© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company. This is an open access article under the CC BY-NC-ND license

(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.引言

列车在运行过程中，由于受到天气、地质条件、运输组织水平的影响，极有可能发生偏离计划列车运行图导致列车晚点及列车间运行冲突的情况。在既有针对列车运行图晚点传播规律[1–3]、动态性能[4,5]、运行调整智能决策等方面的研究中，多以计划列车运行图中提前铺画的冗余时间为列车晚点、运行冲突的唯一消解源，或者采用加入随机干扰的方法模拟后续列车运行可能发生的情况[6–10]。考虑到铁路运营本身的周期性，既有运营过程中的列车晚点统计数据在长期积累下体现出的规律性分布，相比随机加入的干扰时间更加具有说服力。因此，基于历史统计数据将列车运行图中的时间要素进行模糊化处理，并通过模糊时间知识推理进行运行图冲突预测是更合理的。

文献[11]基于赋时Petri网提出了确定时间区间的知识表达和推理方法，文献[12]在此基础上，基于模糊集理论建立了带有四个模糊时间函数的模糊时间高级Petri网模型，并给出了推理算法。这种方法在文献[13,14]中被应用于检查列车运行计划中的时间一致性约束。文超、彭其渊等则利用三角模糊数工作流网将运行模式划分为顺序模式和选择模式两种，提出高速铁路列车运行过程冲突判别、预测方法[15,16]。既有的研究成果为解决将日常运营数据应用于提高冲突预测质量奠定了基础，本文的研究旨在解决以下问题：

(1)如何基于历史运营数据模糊化处理列车运行图中的时间间隔？

(2)运行图冲突的判定条件是什么？如何评价运行冲突？

(3)相比于现有方法，模糊时间知识推理在实际应用中的优势是什么？

本文内容框架如下：第2部分基于赋时库所Petri网建模并给出基于历史运营数据模糊化处理列车运行图时间间隔的方法；第3部分提出高速铁路列车运行图冲突的定义、判定条件及可能性度量方法；第4部分以北京南到济南西的线路为例，在有无外界干扰的情况下分析其冲突预测结果，论证本文提出算法的可行性并与传统的计算结果进行比较，得出结论。

2.建模和数据预处理

2.1. 高速铁路列车运行图的赋时Petri网建模

在既有研究中，列车运行图建模多基于仿真工具和数学模型进行。Petri网是其中一个重要的分支并已用于列车运行图的建模和分析[2,17,18]。赋时Petri网是Petri网发展理论的重要分支之一，按时间赋予方式的不同可以分为赋时变迁Petri网、赋时库所Petri网和赋时有向弧Petri网[2]。考虑到在赋时变迁Petri网中，只有当时间延迟满足后，变迁输出库所内的标识才会改变，从而造成模型标识状态不清晰，因此，本文采用赋时库所Petri网建立高速铁路列车运行图模型，以保证系统状态标识都是准确的。形式化定义高速铁路列车运行图的赋时库所Petri网模型如下：

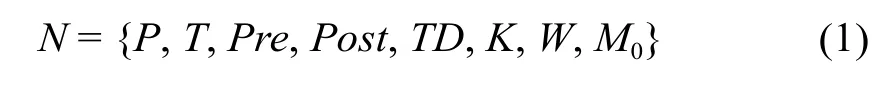
其中，

(1)N为高速铁路列车运行图赋时库所Petri网系统；(2)P= {p1,p2,…,pm}，为有限的库所集，满足，即模型中至少有一个变迁或一个库所，同时没有既是库所又是变迁的元素；

(3)T= {t1,t2,…,tn}，为有限的变迁集，满足

(4)Pre:P×T→ {0, 1}，为系统的前相关函数，0表示库所p与变迁t不相关，1表示库所p是变迁t的输入库所；

(5)Post:T×P→ {0, 1}，为系统的后相关函数，0表示库所p与变迁t不相关，1表示库所p是变迁t的输出库所，Pre与Post共同构成系统内库所与变迁间的关联关系；

(6)TD:P→time,，为库所到模糊时间区间的映射函数；

(7)K、W、M0分别为库所容量函数、有向弧权函数和系统初始标识，且满足K=W= 1，即高速铁路列车运行图系统内的库所只存在是否满足时间约束两种状态，前向约束条件的满足导致变迁的使能，变迁的发生则导致输出库所状态的改变。

以图1为例，该示例中有Tr1、Tr2、Tr3三列高速铁路列车，S1、S2、S3、S4四个车站。根据高速铁路列车运行图中基本时间要素的约束关系建立该示例的Petri网模型，如图2所示。其中，列车和车站以阿拉伯数字标识，区间以罗马数字标识。

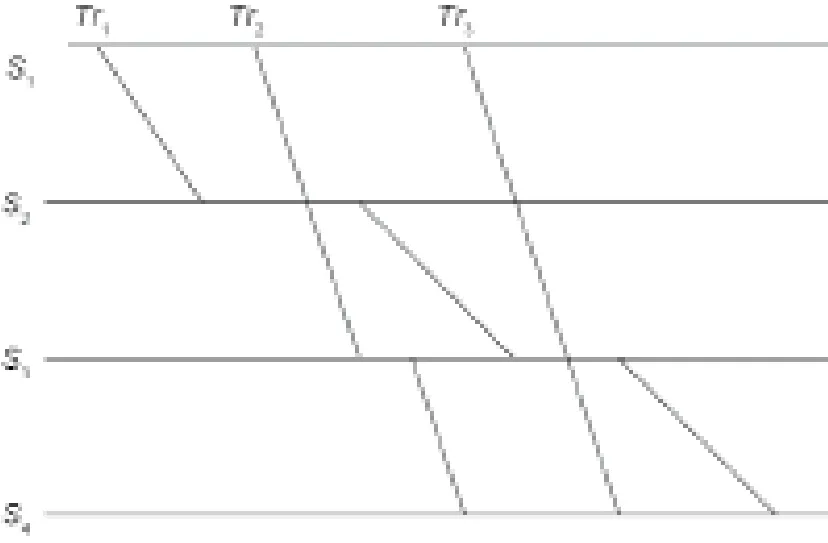
图1.运行图示例。

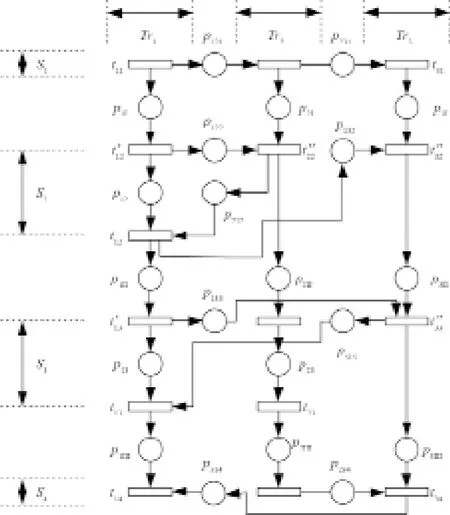
图2.示例运行图Petri网模型。

从这个示例中可以看出，任意一列列车的运行计划是由顺次经过的车站序列和与相邻列车车站作业的间隔时间构成。因此，基于赋时库所Petri网的高速铁路列车运行图模型具有以下特征。一是变迁类型有三种，分别表示列车到达、列车出发和列车通过。库所类型有两种，一种是列车位于车站，一种是列车位于区间，前者时间标识代表同一车站上的相邻列车作业时间间隔，后者时间标识代表列车在区间的运行时分。二是前行列车对后行列车具有一定的时间间隔要求，即后行变迁的时间间隔需要满足前行变迁施加的时间约束和列车运行图规定的时间间隔。基于这些特征，建立基于赋时库所Petri网的列车运行图模型是相对直接和简单的，并为实现下一步的模糊时间知识推理奠定了基础。

2.2 .四角模糊数和模糊处理

在现实生活中，任意一个事件的发生时间可以用一个具体时间表示或者给定一个事件发生可能的时间范围。一般情况下，时间范围相比于静态值能够传递更多信息，此外，模糊化处理后的计划时间间隔是系统实际运行中不确定性的反映，用以提高系统性能。基于时间区间的四角模糊数形式化定义如下：

其中，h为时间取值可能性的最大值；b为事件的最早结束时间；c为事件的最晚结束时间；(a,b)、(c,d)为左右浮动取值区间。图3为一个简单的四角模糊数示例。

考虑到四角模糊数能够传递更多的时间信息，为模糊时间知识推理提供坚实的基础，在下文中将重点阐释如何将静态时间区间转换为四角模糊数。

2.2.1. 单值向时间区间的转化

基于2.1. 部分对高速铁路列车运行图的建模，相邻两个列车作业的时间间隔是一个确定的值，并且被存储在相应的库所中。考虑到在计划列车运行图铺画时会预设一定的冗余时间，因此该确定的单值可以转化为包含冗余时间信息的时间区间。

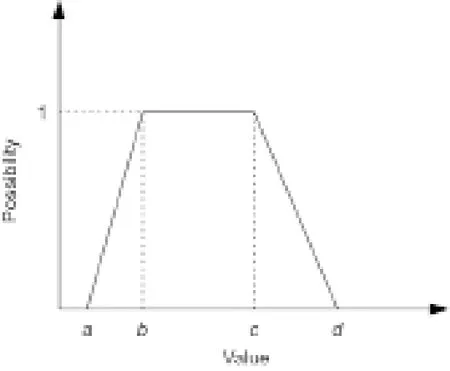
图3.四角模糊梯形数示意。

2.2.2.时间区间到四角模糊数的转化

高速铁路相关的运营单位在列车运行图周期化使用的过程中可以记录大量的实际运行数据，尤其是任意一列列车在车站的到达、出发时间等。需要说明的是，在数据记录阶段列车运行图应保持一致性，避免出现阶段列车运行图调整带来的数据波动。在所有需要的基础数据准备好后，可以实现基础的数据统计分析。以时间间隔Δt为例，假设在数据记录阶段共统计了n次数据，可以计算得到该时间间隔的统计平均值µ和标准差σ。假设这些值是满足泊松分布的，该时间间隔在置信水平α下的置信区间为其中，zα/2可以基于置信水平α通过查询标准正态分布表得到。那么该时间间隔的四角模糊数为其中，r为该时间间隔上预设的冗余时间。

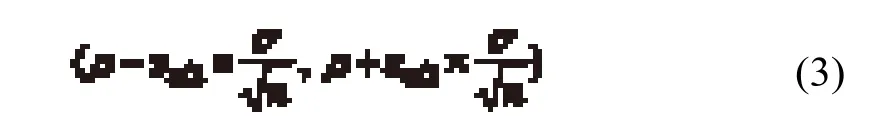
3.冲突预测

3.1. 冲突定义及类型

高速铁路列车运行图追踪列车间隔时间，是指追踪运行的两列列车之间的最小间隔时间。其中，在我国目标距离连续速度控制模式下，高速铁路列车运行图的最小追踪列车间隔为5 min[19]。基于文献[16]中对列车运行冲突的定义，从时间要素约束的角度，高速铁路列车运行图内的冲突主要是由于列车偏离计划列车运行线，导致列车追踪间隔不满足最小追踪间隔时间的状态。根据列车偏离计划列车运行线的程度，高速铁路列车运行图冲突可划分为以下两种。

3.1.1. 潜在冲突PC

潜在冲突PC是指列车在各种干扰的影响下偏离了计划列车运行线，但由于冗余时间的缓冲作用，仍满足最小追踪时间间隔约束，避免了当前冲突的发生。

以图4(a)为例，到达变迁t1由于出发晚点及区间运行时间长于图定时间，实际列车运行线(虚线)偏离计划列车运行线(实线)。变迁t1在经过冗余时间消解后的模糊发生时间推理结果为o(t1) = (A,B,C,D)，变迁t2的模糊使能时间推理结果为o(t2) = (E,F,G,H)。根据列车运行图最小追踪间隔约束，变迁t1发生至少Imin时间后变迁t2才可以发生。因此只有当两变迁的模糊发生时间间隔I≥Imin时，运行图才暂时不会发生冲突。

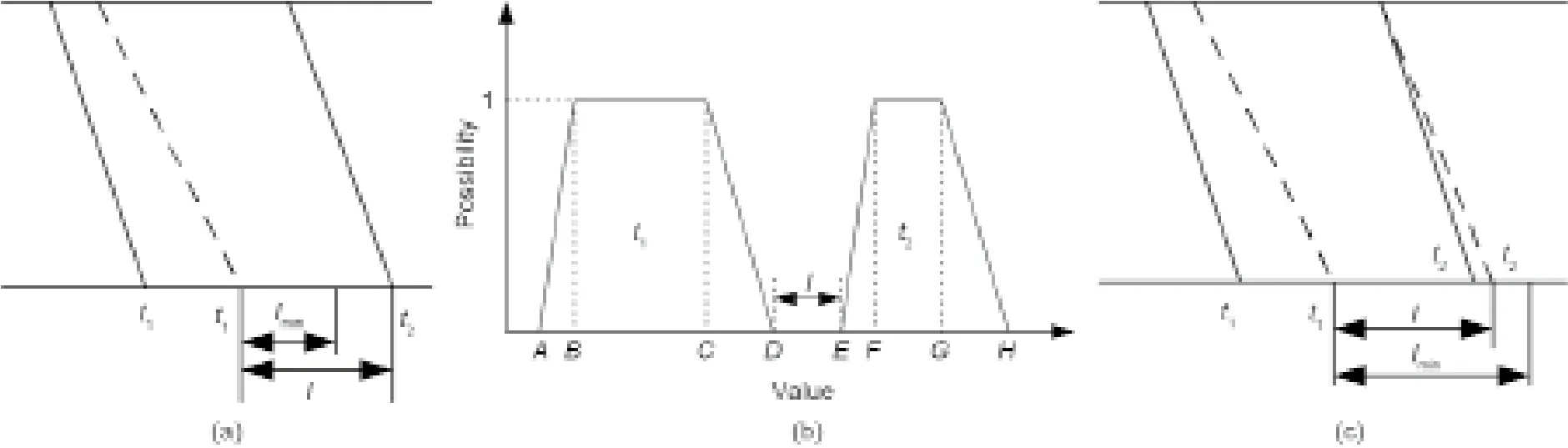
图4.冲突判定示意图。(a)潜在冲突示意；(b)确定冲突示意；(c)模糊发生时间示意。

3.1.2. 确定冲突CC

确定冲突CC是指前行列车偏离计划列车运行线后，冗余时间消减完成后仍然不能满足最小追踪时间间隔约束时，列车间已经发生确定的冲突的状态。如图4(b)所示，当实际追踪间隔时间I＜Imin时确定存在在两变迁间发生冲突的可能性。

3.2. 冲突可能性度量

当前行列车受到运行干扰而产生晚点时，晚点影响范围随着晚点横向、纵向的传播不断扩大。本文并不涉及后续列车的运行调整，因此，运行干扰的影响将在一定的规则下施加到后续每一列列车上。针对列车运行干扰的影响程度评估将从单列列车的运行计划偏离幅度和列车间冲突发生可能性大小两方面进行度量。

3.2.1. 单列列车运行计划偏离

对于单列列车，高速铁路运行图规定的时间间隔体现在模糊时间片π(τ)上。在每一列列车的运行过程中，由于受到列车运行干扰的影响，列车的实际运行线可能偏离计划列车运行线。该偏离程度是列车运行干扰造成的结果，同时是列车运行冲突产生的直接原因。假设运行图内列车i的第j个图定时间区间运行图的实际运行情况即模糊时间知识推理的结果为时，我们称列车i的第j个图定时间区间发生偏离，如图5所示。该列车的第j(j=1,2,3,…,D)个图定时间区间的运行偏离度ηij可计算如下：

其中，S(ABCD)为梯形ABCD的面积；S(ABCD∩EFGH)为梯形ABCD与梯形EFGH的重合面积。该列车i在⊿个图定时间区间的总体平均偏离度ηi为

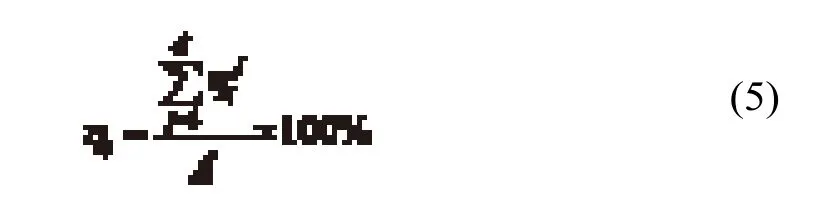
显然，列车总体平均偏离度越大，对其他相邻列车的运行干扰越大，产生运行冲突的可能性越大。

3.2.2.列车间冲突可能性

根据前文中对不同冲突类型的定义和判定条件，当高速铁路列车运行图内发生晚点传播时，需要首先确定冲突类型。若为潜在冲突，则在该时间区间内不会发生冲突；若为确定冲突，则基于变迁的模糊发生时间计算其冲突可能性。

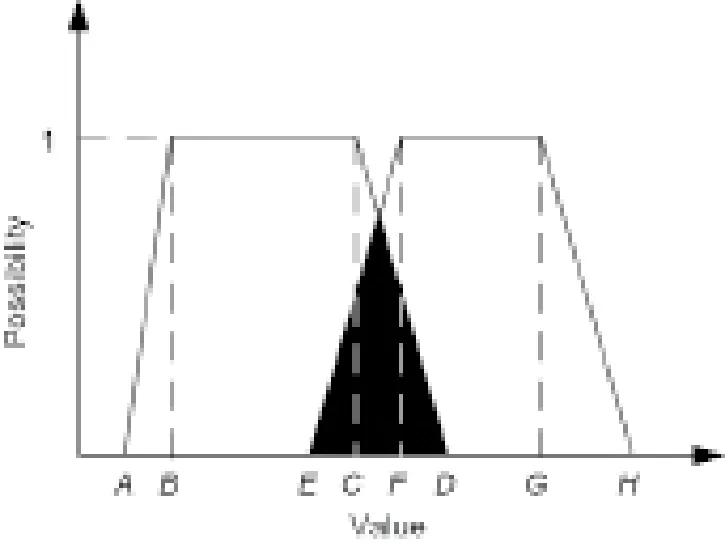
图5.单列列车运行计划偏离示意图。

以图6(a)为例，变迁t1、t2为高速铁路运行图内存在时间间隔约束的两变迁，其中，变迁t1的模糊发生时间为o(t1) = (A, B, C, D)，变迁t2的模糊使能时间为o(t2) = (E, F, G, H)，且两变迁间的时间间隔I 小于最小时间间隔Imin。此时，完全消解变迁间冲突所需的最小冗余时间总量R = Imin– I，而变迁t1、变迁t2的可用冗余时间分别为因此，对变迁t1、t2的模糊时间更新如下。

根据冗余时间利用的紧前原则，先令变迁t1的冗余时间剩余量则变迁t1的的冗余时间已经实现冲突的完全消解，不变；否则，令变迁t2的冗余时间剩余量在完成冗余时间的冲突消解后，两变迁的时间间隔更新为，变迁t1更新后的模糊发生时间为，变迁t2更新后的模糊使能时间为更新后的变迁间隔关系如图6(b)所示，从阴影部分面积变化可以看出冗余时间对冲突的消解作用。此时，两变迁之间的冲突可能性δ12可计算如下：

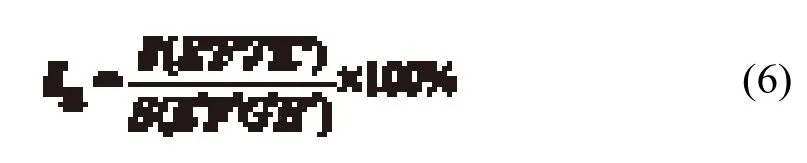
同样，两变迁间的冲突可能性越大，后行列车受到前行列车晚点传播的影响越大。

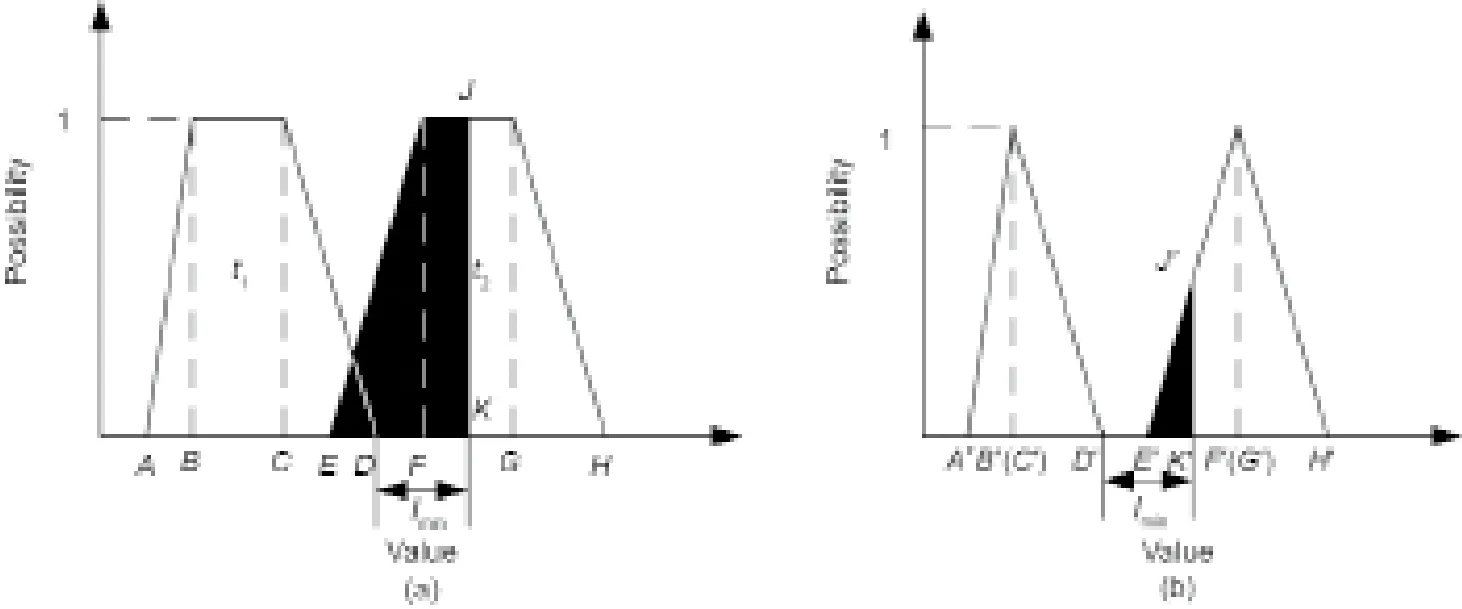
图6.列车间冲突示意图。(a)冗余时间消解前；(b)冗余时间消解后。

3.3. 冲突预测算法

基于SQL数据库和C#仿真平台实现高速铁路列车运行图的车站冲突预测。其中SQL数据库主要用于存储计划列车运行图数据、历史实绩运行图数据，模糊化处理计划列车运行图并得到事件触发时间间隔约束的模糊延迟时间数据；C#则基于由SQL数据库导入的基础数据，并将这些数据转化为赋时库所Petri网中库所与变迁间的关联关系，将模糊延迟时间分配到相应的库所。基于模糊时间知识推理进行冲突预测，记录冲突预测结果，计算评价指标并输出结果。冲突预测的实现步骤如下：

(1)上述已知或可知信息的获取与整理。包括计划列车运行图和历史实绩列车运行图两部分，此外，根据模糊时间知识推理可以在运行图实际运用中的任一时刻进行，即推理的初始条件可以根据仿真实验的需要进行改变。

(2)基于模糊时间知识推理进行自上而下、自左向右的冲突预测。对存在最小追踪间隔时间约束的前后列车进行冲突判定，若判定结果为确定冲突，则更新变迁的模糊时间分布并计算冲突可能性δ，然后以更新后的模糊时间分布进行下一次的模糊推理，循环进行，直至遍历所有变迁。以图7中变迁t11、t'22间的冲突预测为例，该冲突预测实现的是车站S2上列车Tr1的到达与列车Tr2的通过间的冲突检测。在该示例中，列车Tr1在车站S1的发车时间即变迁t11的模糊发生时间为o(t11) = (0, 0, 0, 0)，相关库所的模糊延迟时间如表1所示，其推理过程如图7所示。

表1.真初始数据

(3)仿真结果的统计分析。在完成所有的模糊时间知识推理后，统计运行图冲突发生总次数∑及单列车平均偏离度ηi。此外，在本文的仿真案例中，除了这两个指标外，仿真平台对冲突发生位置的冗余时间的利用情况也进行了标记，可为下一步进行计划列车运行图冗余时间铺画调整提供辅助决策。

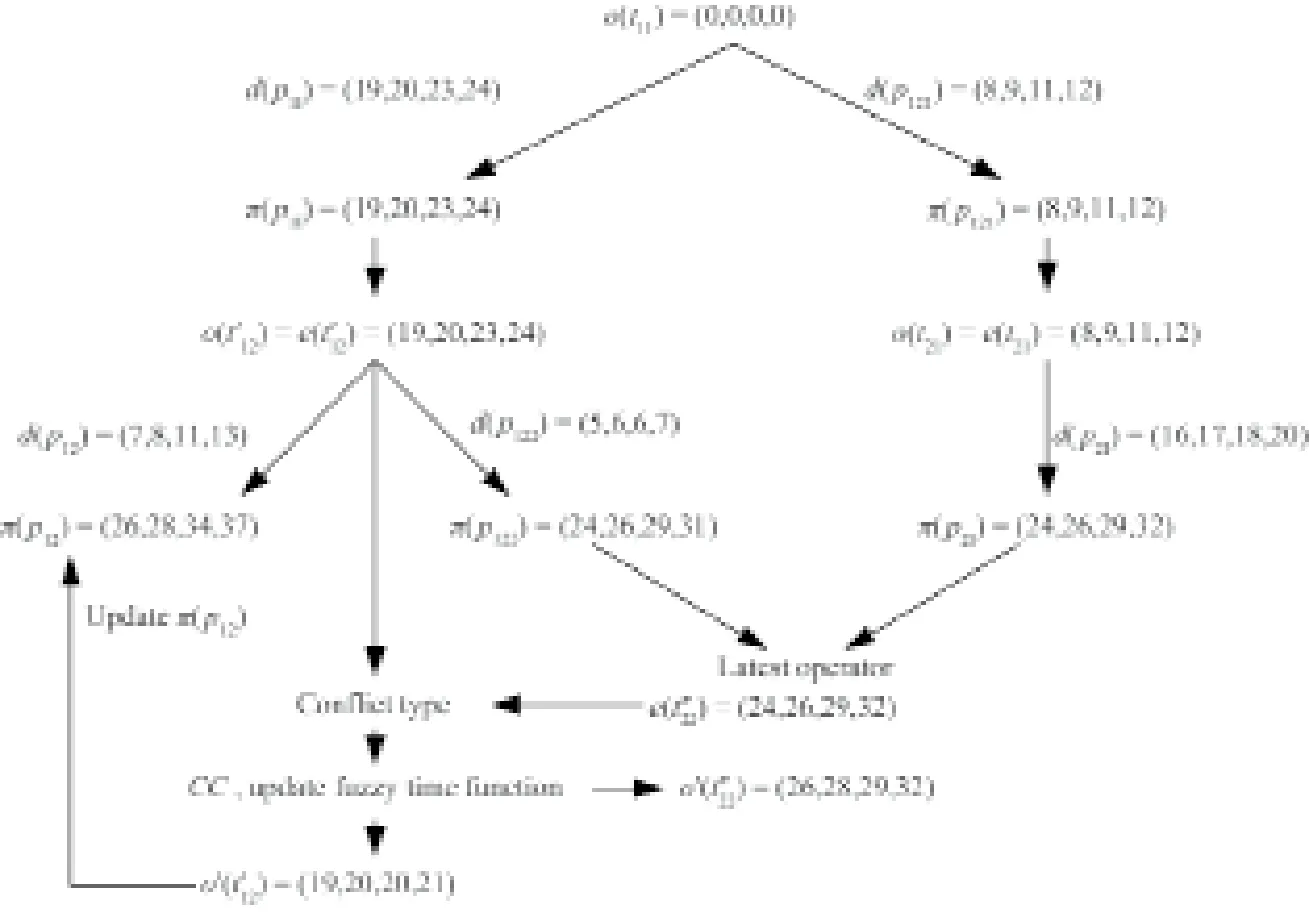
图7.模糊时间知识推理示意图。

4.仿真算例

4.1. 仿真实验设计

一定程度上，一条真实高速铁路线路的实际运营数据的获取是困难的。因此，我们基于京沪高铁中的北京南–济南西路段的线路数据生成一个包含6个车站、15列列车的虚拟高速铁路列车运行图。该实际线路及虚拟运行图分别如图8、图9所示。虚拟运行图基于历史运营数据的模糊化处理，通过随机数实现如下：时间间隔的左浮动区间为1～2 min，右浮动区间为1～3 min。尽管在仿真实验中我们通过随机数模糊化处理列车运行图中的时间间隔，但本文2.2.部分提出的模糊处理方法在实际运用中依然是有效的。同时，实验中列车运行图的虚拟化及基于随机数的模糊化处理并不影响模糊时间知识推理过程。

基于初始数据，在基于赋时库所Petri网对该虚拟运行图建模后，以四角模糊数呈现的时间因素作为模糊延迟时间被分配到相应的库所中。仿真实验在两种不同的情境集下进行。在情境1中为无任何额外干扰情况下基于模糊时间知识推理的冲突预测。由于运行图内的时间间隔均进行了模糊化处理，因此该情境下的冲突预测结果可以反映列车运行图的铺画质量和性能。在情境2中，额外的运行干扰被添加到冲突预测中。该情境下，列车G203从北京南的出发时间比图定时间晚点10 min。尽管两种情境下的冲突预测过程基本相同，但是通过对比两种情境下的仿真结果，可以忽略列车运行图本身的影响，实现对列车运行图铺画质量、动态灵活性的评价。

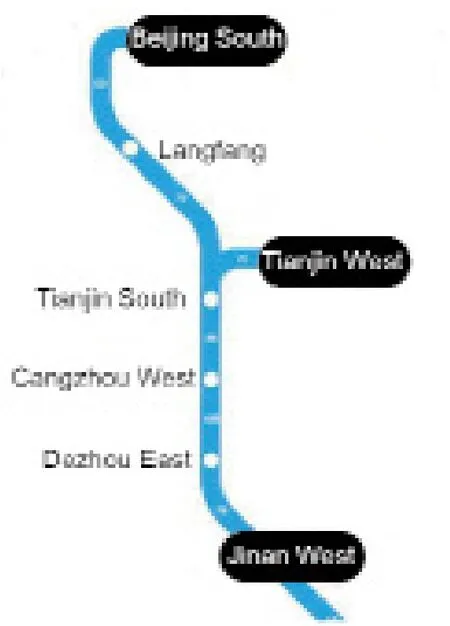
图8.北京南到济南西线路示意图。

4.2. 仿真分析

两种情境下的结果分析包括以下三个部分。第一部分冲突预测的结果以图表显示，并在新的运行干扰产生或列车调度做出新的运输调整后进行相应的更新。更新后的冲突预测结果可为调度员提供当前或后期可能的包括潜在冲突发生的地点、冲突发生可能性的潜在冲突信息。对于该冲突预测结果对应该次运行调整，冲突预测结果本身可提前评价该冲突调整策略的作用效果。第二部分对比分析了基于模糊时间知识推理的冲突预测方法与现有的冲突预测方法。在现有的冲突预测方法中，列车调度以后续列车运行线静态确定为假设条件，疏解当前冲突且只显示当前确定冲突。在该部分中对比了两种方法下冲突预测结果给出的信息量。在第三部分主要进行两种不同情境下的冲突预测结果对比。

4.2.1. 冲突预测结果展示

冲突预测的结果基于3.2.部分中提出的两个评价指标。冲突预测每执行一次，单列列车的总体偏离度和相邻列车作业的冲突可能性计算一次并显示在折线图中。图10为列车运行图内每列列车偏离度，并且任意一列列车的任意一个时间间隔的模糊偏离程度都可以做进一步的分析，如图10(a)所示。以列车G203为例，图10(b)为列车在每一个时间间隔内的偏离程度，该偏离程度分布图为调度员理解列车总体偏离程度提供了数据支持。每一个潜在冲突包括冲突发生地点、冲突发生可能性、冲突完全消解所需要的冗余时间和当前冗余时间的利用情况。总体上来讲，调度员还应该知道潜在冲突的总数。图11(a)为所有潜在冲突的示意图，且任意一个冲突可进一步细化为以上四个要素的冲突信息，如图11(b)所示。

图9.运行图示例。

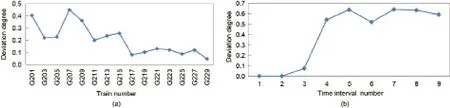
图10.偏离度指标。(a)单列列车总体偏离度；(b)G203列车的偏离度分布。

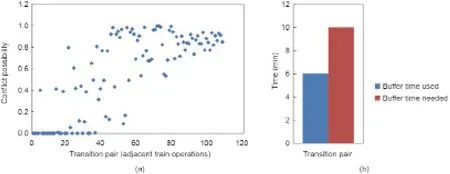
图11.冲突可能性指标。(a)冲突可能性分布；(b)变迁(DT008，DT0024)的冲突信息。

4.2.2.两种冲突预测方法的对比

对于调度员来说，冲突预测的结果应该为运输调整提供充足的信息，但同时过多的信息会为调度员做调度决策带来压力和困难。在现有的方法中，调度系统提示调度员当前确定的冲突信息，同时假设后续列车运行计划不会再受其他运行干扰的影响，因此，该方法只专注于当前的运行环境和当前冲突的结果，而不能定位到冲突产生的原因。两种方法下的冲突预测结果信息量对比如表2所示。

通过表2中的两种方法对比可知，本文提出的基于模糊时间知识推理的列车运行冲突预测结果可以为调度员提供更多更有效的信息，让他们掌握即将发生的运行状况，并在下一步的列车运行图调整中保持列车的灵活性和鲁棒性。

4.2.3. 两种不同情境下的冲突预测结果对比

如图10、图11所示，尽管计划列车运行图中没有任何冲突，但是在未添加任何额外干扰下基于模糊运行图的预测结果中同样存在潜在冲突。造成这一现象的主要原因是相比于计划时间间隔，模糊化处理后的时间间隔加宽造成相邻列车作业时间间隔小于最小追踪间隔要求。这一现象带来了另一个问题，如何让调度员区分基于模糊时间知识推理的冲突预测结果是由于外在干扰引起的还是由列车运行图铺画质量本身决定的，或者两者都有？因此，两种情境下的冲突预测结果对比是必要的。图12为两种情境下的冲突预测结果分布情况。

在仿真结果分析中，有一个比较有趣的现象是情境2中存在冲突可能的地方在情境1中反而减少了，甚至降低为零。这意味着情境2中额外的运行干扰反而降低甚至消解了部分冲突。以变迁对比组(DT008，DT0024)和(DT0022，DT0028)为例，对比组内的两个变迁代表了两个相邻列车作业并需要进行运行冲突检测，其中，变迁DT008和DT0024分别表示列车G201到达德州东车站和列车G205通过德州东车站。变迁DT0022和DT0028分别表示列车G205和列车G207通过天津车站。如图13所示，变迁对比组(DT008，DT0024)的冲突可能性在情境2中完全消解，而变迁对比组(DT0022，DT0028)在情境2中的冲突可能性直线下降。这一现象侧面说明额外的运行干扰并不一直是负面的，其在一定程度上可以与预设的冗余时间一样用于实际运行中的冲突消解。然而额外的干扰造成冲突的可能性增加并使运行环境更加复杂。

表2.种方法的信息量对比

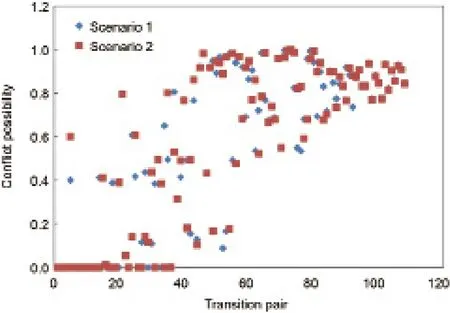
图12.冲突可能性分布对比。

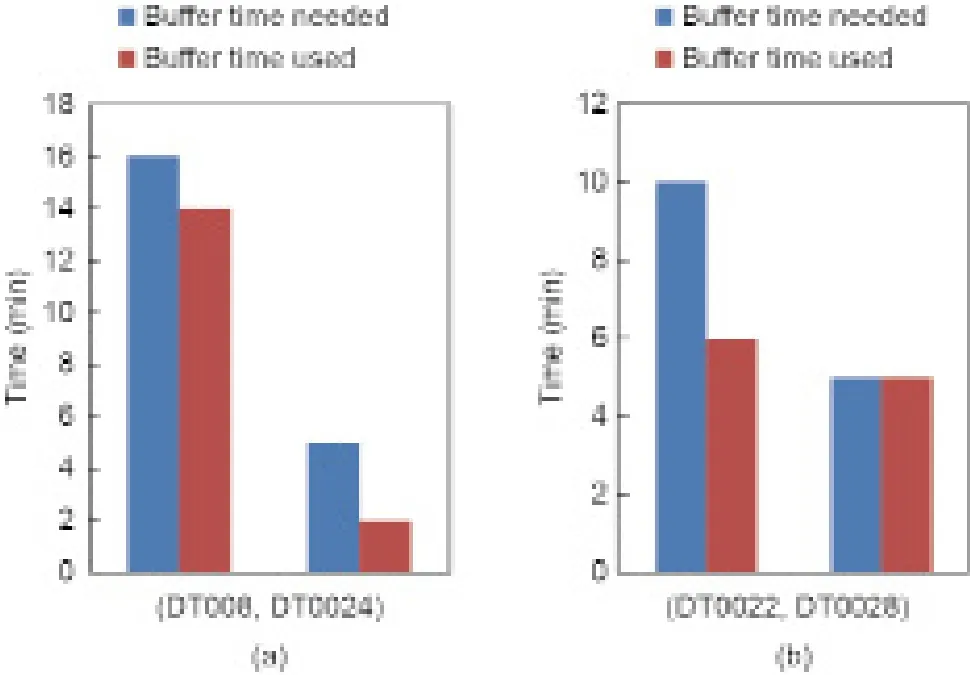
图13.冲突可能性对比。(a)变迁对比组(DT008，DT0024)；(b)变迁对比组(DT0022，DT0028)。

5.结论

基于历史统计数据的计划列车运行图时间间隔模糊化处理，相较于传统的随机干扰引入，更能够体现高速铁路列车运行图对象在实现过程中的特性及规律。而模糊化处理后的计划列车运行图，在面对外部干扰时，除了传统方法中冗余时间的缓冲消解作用之外，模糊浮动区间本身同样为晚点时间传播消解起到了一定的缓冲作用。通过本文在两种不同情境下的冲突预测结果，可以得到以下结论：

(1)传统的计划列车运行图只是简单实现了资源占用检查，并加入一定的冗余时间增强系统的鲁棒性。但是基于静态确定的计划列车运行图的冲突预测，由于隐含了后续列车严格按照计划列车运行线运行的假设条件，预测结果并不可靠；

(2)模糊化处理的计划列车运行图是高速铁路列车运行图实际运营的效果叠加，是高速铁路列车运行图铺画质量的侧面反映。该情况下的冲突预测结果可以用于该运行图铺画质量评价，同时为下一次的运行图调整提供指导意见。

(3)在模糊化处理的计划列车运行图上施加运行干扰，是对运行图实际运用的模拟。该情况下的运行图冲突预测可以用于指导当前运行调整策略的制定。即在冲突产生、运行调整策略制定后均进行一次基于模糊时间知识推理的冲突预测，通过对比调整前后冲突发生情况，在调度调整命令正式下达前评价当前运行调整策略效果，从而更加高效安全地指导列车运行。

下一步的研究将从以下几个方面展开：一是基于本文模糊化时间知识推理用于高速铁路列车运行图冲突预测的流程及评价指标计算，通过提取高速铁路列车运行图形式化建模的共通点，实现更大规模的冲突预测推理，进一步提高本文研究成果的现实应用价值；二是研究冗余时间设置与高速铁路列车运行图内时间要素的浮动区间在对列车晚点、冲突消减过程中的协同关系，为高速铁路列车运行图的冗余时间设置提供建议。

Acknowledgements

This work was supported by the National Nature Science Foundation of China (U1234206 and 61503311). We acknowledge support under the Railways Techno logy Development Plan of China Railway Corporation (2016X008-J) and the Fundamental Research Funds for the Central Universities (2682015CX039). Parts of this work were supported by the National United Engineering Laboratory of Integrated and Intelligent Transportation. We are grateful for useful contributions made by our project partners.

Compliance with ethics guidelines

He Zhuang, Liping Feng, Chao Wen, Qiyuan Peng, and Qizhi Tang declare that they have no conflict of interest or financial conflicts to disclose.

[1] Meng LY, Goverde RMP. A method for constructing train delay propagation process by mining train record data. J B Jiaotong Univ 2012;36(6):15—20. Chinese.

[2] Goverde RMP. A delay propagation algorithm for large-scale railway traffic networks. Transport Res C-Emer 2010;18(3):269−87.

[3] Mozzarella M. A traffic management system for real-time traffic optimization in railways. Transport Res B-Meth 2007, 41(2):246—74.

[4] Landex A, Jensen LW. Measures for track complexity and robustness of operation at stations. J Rail Transport Plan Manage 2013;3(1−2):22—35.

[5] Meng L. Train timetable on-line performance and simulation system on railway passenger dedicated line [dissertation]. Beijing: Beijing Jiaotong University; 2010. Chinese.

[6] Hallowell SF, Harker PT. Predicting on-time performance in scheduled railroad operations: methodology and application to train scheduling. Transport Res A-Pol 1998;32(4):279—95.

[7] Meng LY, Ran F, Wang ZQ. Research on redundant time optimized layout system in train timetabling process on high-speed railway. Railway Comput Appl 2012;21(6):28—30. Chinese.

[8] D’Ariano A, Pranzo M, Hansen IA. Conflict resolution and train speed coordination solving real-time timetable perturbations. IEEE Trans Intell Transport Syst 2007;8(2):208—22.

[9] Larsen R, Pranzo M, D’Ariano A, Corman F, Pacciarelli D. Susceptibility of optimal train schedules to stochastic disturbances of process times. Flex Serv Manuf J 2014;26(4):466−89.

[10] Zhou MH. Urban rail traffic organization scheduling adjustment method. Appl Mech Mater 2013;433−5:1361—5.

[11] Murata T. Temporal uncertainty and fuzzy-timing high-level Petri nets. In: Billington J, Reisig W, editors Proceedings of the 17th International Conference on Application and Theory of Petri Nets; 1996 Jun 24−28; Osaka, Japan. London: Springer-Verlag; 1996. p. 11−28.

[12] Zhou Y, Murata T. Petri net model with fuzzy timing and fuzzy-metric temporal logic. Int J Intell Syst 1999;14(8):719—45.

[13] Ye YD, Du YH, Jia LM. Operation system model of train group with objectoriented Petri subnet. China Railway Sci 2002;23(4):81—8. Chinese.

[14] Liu CH, Du YH. The distributed simulation of train group operation model based on object-oriented Petri subnet. China Railway Sci 2006;27(1):109—14. Chinese.

[15] Wen C, Peng QY, Chen YH, Ren JJ. Modelling the running states of high-speed trains using triangular fuzzy number workflow nets. P I Mech Eng F-J Rai 2013;228(4):422−30.

[16] Wen C, Li JG, Peng QY, Li BY, Ren JJ. Predicting high-speed train operation conflicts using workflow nets and triangular fuzzy numbers. P I Mech Eng F-J Rai 2013;229(3):268—79.

[17] Wang P, Ma L, Goverde RMP, Wang QY. Rescheduling trains using Petri nets and heuristic search. IEEE Trans Intell Transport Syst 2015;17(3):1—10.

[18] Milinkovi S, Markovi M, Veskovi S, Ivi M, Pavlovi N. A fuzzy Petri net model to estimate train delays. Simulat Model Pract Th 2013;33:144—57.

[19] Tian BW. Research on technical standards of basic elements in train diagram for high-speed railway [dissertation]. Chengdu: Southwest Jiaotong University; 2012. Chinese.

* Corresponding author.

E-mail address:lipingfeng@my.swjtu.cn

2095-8099/© 2016 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company.

This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

英文原文: Engineering 2016, 2(3): 366—373

He Zhuang, Liping Feng, Chao Wen, Qiyuan Peng, Qizhi Tan. High-Speed Railway Train Timetable Conflict Prediction Based on Fuzzy Temporal

Knowledge Reasoning. Engineering, http://dx.doi.org/10.1016/J.ENG.2016.03.019

列车运行图

模糊时间函数

冲突预测