船桥碰撞中各因素对船撞力影响的研究

2016-03-10宗莉娜刘伟庆

江苏船舶 2016年6期

关键词：撞击力吨位桥墩

宗莉娜,刘伟庆,方海,庄勇

(1.江苏开放大学建筑工程学院，江苏南京 210036；2.南京工业大学土木工程学院，江苏南京 210009；3.中铁大桥勘测设计院集团有限公司，湖北武汉 430034)

船桥碰撞中各因素对船撞力影响的研究

宗莉娜1,刘伟庆2,方海2,庄勇3

(1.江苏开放大学建筑工程学院，江苏南京 210036；2.南京工业大学土木工程学院，江苏南京 210009；3.中铁大桥勘测设计院集团有限公司，湖北武汉 430034)

对国内外常用的桥梁船撞力简化计算公式进行了讨论和分析，剖析了国内现有的规范公式所存在的问题。通过大量的船舶撞击刚性墙的数值模拟，研究船舶速度、吨位、接触面积对船撞力大小的影响。

船桥碰撞;有限元仿真;船撞力

0 引言

船舶撞击桥墩结构产生的撞击力与多种因素相关，如船头形式、船舶吨位、碰撞方向、运行速度、水的作用、桥墩刚度以及桥墩截面形状和尺寸等。即使是撞击相同的桥，不同的撞击条件下所得到的船撞力大小也各有不同。此外，船艏的结构形式和尺寸也将会影响撞击作用时接触面的大小和形状。由相关研究可以发现：同一吨位级别但不同类型的船舶，由于船艏结构形式与尺寸大小不同，导致的碰撞作用也有所差异。本文主要研究船舶吨位、船舶运行速度、船艏的结构形式以及船桥碰撞的接触面积等因素对船撞力大小的影响，从而分析得到船撞力与各影响因素之间的内在规律。

1 船桥撞击力经验公式及其比较

1.1 桥梁船撞力的实用计算方法

由于船撞问题的复杂性，各国学者也都进行研究，所以用于计算船撞力的经验公式也较多，主要有以下几种。

1.1.1 美国公路桥涵设计规范公式

1991年，美国各州运输官员协会(AASHTO)颁布了《公路桥梁防撞设计指南》，提出船撞力的经验公式为：

P=0.98(DWT)1/2(v/8)

(1)

1994年将公式修改为：

(2)

式中：P为等效静态撞击力，N；v为撞击速度，m/s；DWT为船舶载重吨位，t。

1.1.2 欧洲规范公式

1999年，欧洲规范Eurocodel提出船舶的撞击力可以按照式(3)计算。

(3)

式中：K为船舶的刚度，其中，内陆航道K=5MN/m、v=3m/s，海洋航道K=15MN/m、v=3m/s；M代表船舶质量，kg。

1.1.3Woisin公式及其修正

Woisin教授对散装货船与刚性墙的碰撞进行了缩尺模型试验，从而归纳得到了散装货船撞击桥墩的平均撞击力的简化公式：

(4)

1.1.4 我国公路桥涵设计通用规范公式

通航河道中的桥梁结构所受到的船舶撞击力大小，可以近似按漂流物撞击进行计算：

P=Gv1/(gt)

(5)

式中：P为漂流物撞击力，N；G为漂流物重力，kN；v1为水流速度，m/s；t为撞击时间，一般取1s；g为重力加速度，m/s2。

1.1.5 我国铁路桥涵设计基本规范公式

我国《铁路桥涵设计基本规范》[1]中将船舶与桥梁结构的撞击力等效为一偶然载荷，也是采用的“静力法”进行计算，即假定船舶的初始动能全部转化为船撞力所完成的总功。假设船舶的质量为m，运行速度为v2，撞击角度为α，根据碰撞前后的功能互等原理得到撞击力：

(6)

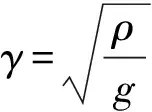
1.1.6 其他经验公式

挪威路桥局规定了船舶撞击桥梁的碰撞力大小公式为： P=3.5(DWT)1/3。北欧道路局对渡轮撞击桥梁的碰撞力取为： P=0.5(DWT)1/2。国内，钱铧[2]基于对船桥碰撞的研究，提出了船撞力公式：

式中：Ca为反映P和M、v的相关参数；Cb为桥墩的刚度变化时船撞击力变化的参数。

此外，同济大学王君杰[3-5]、上海交通大学船舶与海洋工程学院刘建成等[6-7]也进行了很多研究。

1.2 国内外规范经验公式对比分析

根据以上经验公式取2 000～30 000t船舶进行计算。由于欧洲规范规定内河航道速度取3m/s，所以对于各公式中的水流速度、撞击速度、运行速度都取v=3m/s。根据各公式计算的结果见图1。

图1 各规范船撞力与船舶吨位的变化

从图1的计算结果可以看出，我国铁路桥规公式(γ=0.3)计算得到的船撞力结果始终最小，且是远远小于其他公式的计算结果。公路桥规公式曲线斜率较陡，在船舶吨位较小时其计算结果较小，但随着船舶吨位变大的过程中计算值变化太大。

2 船桥碰撞力的影响因素分析

本文采用ANSYS/LS-DYNA进行数值计算，研究各因素对船撞力的影响。

2.1 船舶参数及有限元模型

2.1.1 船舶质量及尺寸

本文采用的船舶吨位级别主要有1 000、3 000、5 000 t这3种。各吨位船舶的具体参数见表1，表中，船高代表船舶型深。

表1 不同吨位船舶的各类参数表

2.1.2 船舶的有限元模型

船桥接触碰撞过程中结构发生了很大的非线性变化，如船舷结构会发生屈曲、压溃等破坏现象，因此要确保整个撞击过程的真实性，必须准确地模拟船舷的形状和构造。图2为各种吨位船舶的有限元模型[8]。基于效率和精度两方面的考虑，将计算模型的船头处的网格划得很密，向后逐渐变疏；认为船身部分并不发生变形，而假设为刚性体，以便可以精细地模拟船头处的压溃变形及破坏。

图2 船舶有限元模型

2.2 船舶运行速度

船舶的吨位和运行速度直接决定了发生船桥碰撞时的总能量大小。国内的公路和铁路规范、美国规范以及欧洲规范均将船舶运行速度对碰撞力的影响作用直接表示为：船撞力与速度大小完全成正比关系，由此说明，运行速度对船舶撞击作用的影响是很显著的。

本文以1 000 t级船舶为模型，分别取船舶碰撞速度为1、4、6 m/s。3种工况下的船撞力时程曲线如图3所示。

图3 不同速度下的船撞力时程曲线图

从图中看出，船撞力的最大值随着速度的增加而增大。当速度分别为1、4、6 m/s时，所相应的船撞力最大值分别为3.16、13.04、18.79 MN，船撞力达到最大峰值的时间分别为0.81、0.77、0.74 s，其比值为：1：4.13：5.96，与速度的比值1：4：6非常接近，因而可以近似认为最大船撞力与运行速度和之间呈线性增长。

为了更好地反应最大船撞力与速度之间的关系，进一步模拟了3 000、5 000 t船舶在不同速度下的撞击情况，并且增加了2、8 m/s这2种速度。具体的计算结果见表2。

表2 各吨位船舶在不同速度下的船撞力计算结果

将表中的计算结果绘于图4。从图中可以发现，船撞力的最大值与船舶速度之间的关系基本上是呈线性增长的趋势。

图4 船舶撞击力与速度的关系

2.3 船舶吨位

由表2结果得到的不同速度下船舶撞击力与吨位的关系曲线图如图5所示。图中，最大撞击力与船舶质量或吨位成非线性关系，而且其增长趋势比较符合幂函数规律，因此可采用幂函数的形式对其进行拟合。选用幂函数y=axb的形式，可以拟合出各船舶速度下的船撞力与吨位的关系曲线。

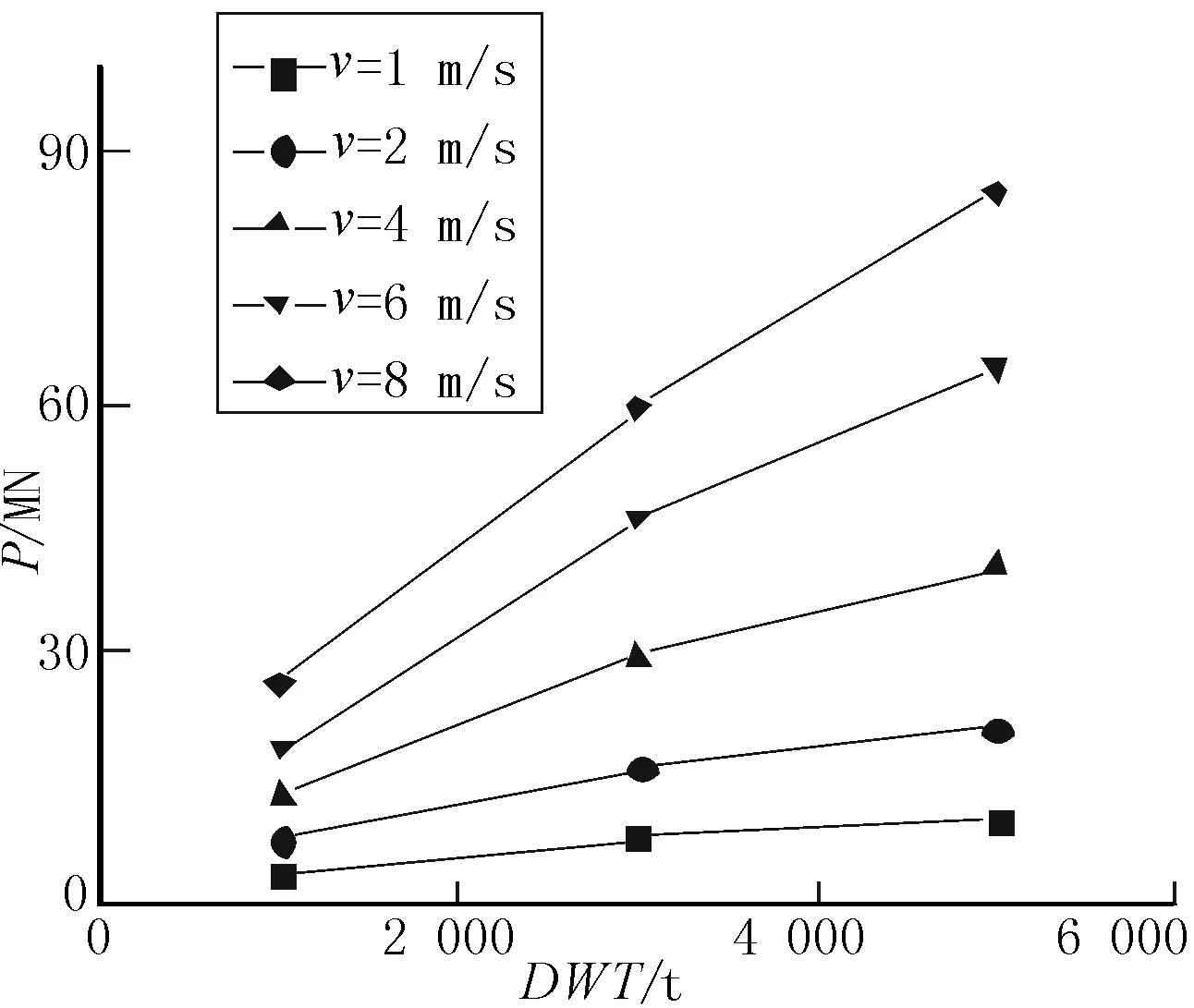
图5 船舶撞击力与吨位的关系

具体拟合过程中得到的各参数取值见表3。

表3 船撞力与墩身宽度关系曲线的拟合结果

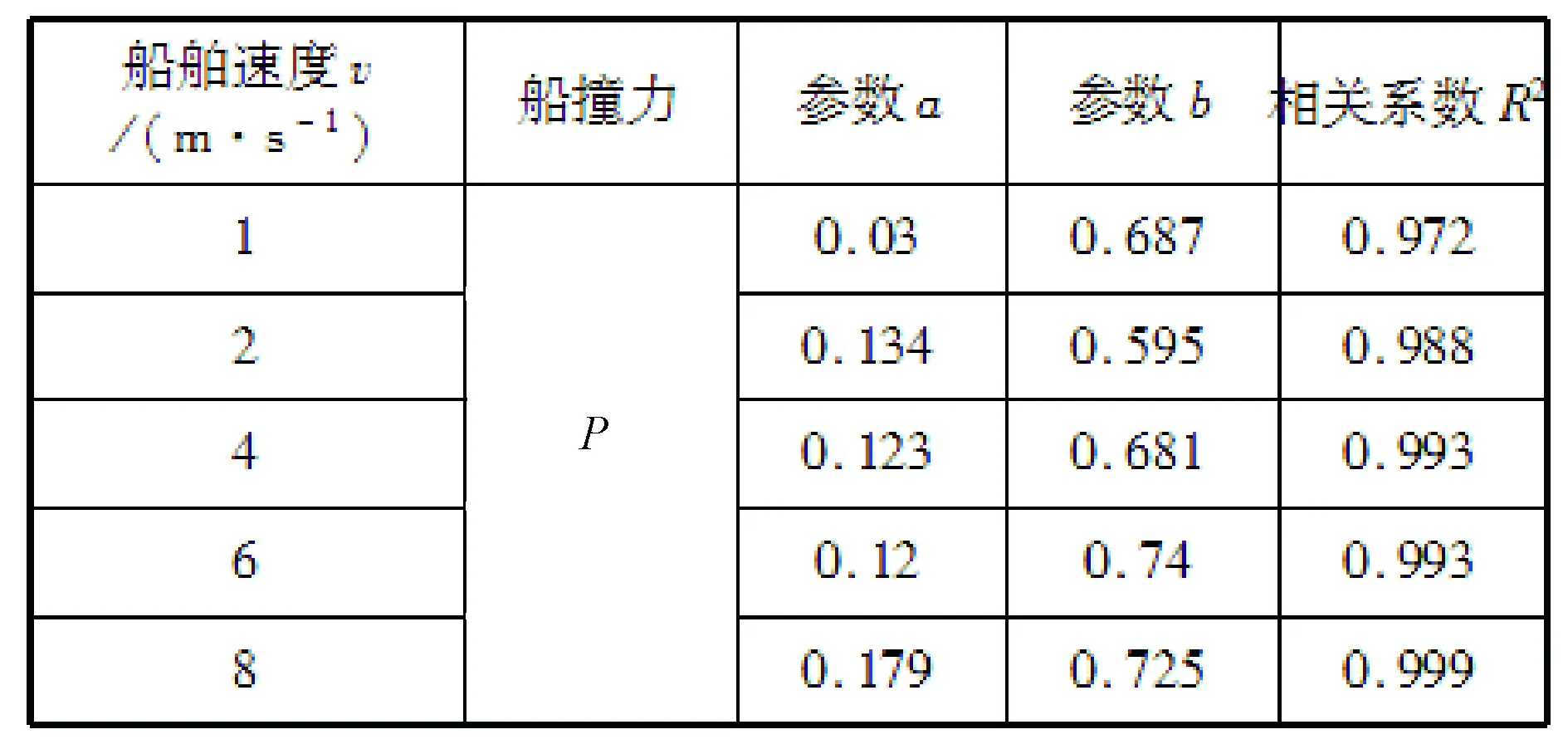
由表3的拟合结果可以发现：幂次方b均是介于0.5～1.0之间，因此，船舶撞击力既不是国内铁路桥规中与船舶吨位成正比的关系，也不是美国规范和修正的Woisin公式中的与船舶吨位开方成正比的关系，而应该是介于两者之间。

2.4 船桥碰撞接触面积

在船桥碰撞事故中，由于不同的水位以及不同桥墩类型等因素都会影响船舶与桥墩碰撞时的接触面积的大小，而接触面积的大小可能会对船桥碰撞力产生影响，因此，有必要研究不同撞击接触面积对船撞力的影响。

本文模拟了3 000 t船舶与刚性墙的3种不同相对位置的碰撞工况，即整个船艏与刚性墙完全接触、仅让船的整个球鼻部分与刚性墙发生碰撞以及仅让船球鼻的下部分与刚性墙发生碰撞。3种工况的船桥碰撞模型和计算结果分别如图6、图7所示。

图6 不同接触面积下船与刚性墙碰撞模型

图7 船艏不同接触面积下的船撞力比较

从图7可以看出，3种碰撞情况下船撞力峰值分别为：27.20 MN(整个船头撞击)，17.36 MN(整个球鼻撞击)，15.82 MN(部分球鼻撞击)。这一结果说明当接触面积越大时船撞力的峰值也越大。

此外，当整个船头与刚性墙接触时碰撞过程持续了约1.41 s；当整个球鼻与刚性墙接触时，碰撞过程持续了1.79 s；当仅有部分球鼻与刚性墙接触时，碰撞过程则持续了1.85 s。从上述现象发现，当接触面积增大时撞击过程的总时间会减少。之所以会产生以上的现象，很可能是因为：在相同条件下，当接触面积大时，2个相撞的物体之间产生相互作用力也增大了。从整个系统的动量转化来看，首先是船舶的动量不断地减少直至为零，然后受到桥墩的反作用而获得少量的反向动量。

船撞力对时间的积分结果见表4。从表4中的各积分结果发现，3条船撞力时程曲线与坐标轴所围成的面积即冲量相当接近。因此，尽管接触面积有所不同，但可以认为在碰撞过程中∫f(t)dt的取值是近似相同的，即虽然船桥碰撞的部位不同，碰撞过程中总的冲量是接近的[9]。