三线铁路大跨度连续弯梁简化计算研究
2016-03-09宋树峰
宋树峰
(铁道第三勘察设计院集团有限公司, 天津 300142)
三线铁路大跨度连续弯梁简化计算研究
宋树峰
(铁道第三勘察设计院集团有限公司, 天津 300142)
三线铁路弯梁桥具有桥面宽、结构宽跨比大、部分截面扭矩大、受力复杂的特点,且目前国内铁路桥梁上可供借鉴的设计、研究经验较少。文章以北京动车段工程跨京开高速公路特大桥三线铁路预应力混凝土连续弯梁为研究对象,通过有限元程序,分别建立了该桥的直梁和弯梁单元模型,在对两组模型各项内力对比分析以及借鉴公路桥梁设计成果的基础上,得出了该桥可以采用直梁模型进行结构总体受力分析的结论,进而简化了该三线连续弯梁桥的结构计算方式,降低了设计难度、提高了设计效率,同时也可为同类桥梁的设计与计算提供参考。
三线铁路; 弯梁; 直梁; 简化计算; 有限元
1 概述
单、双线连续梁桥面较窄,宽跨比较小,箱梁截面整体受力较均匀,基本符合梁元模型的平面假定。而三线梁桥面较宽,宽跨比较大,箱梁截面在受力上较复杂。三线铁路大跨度连续弯梁桥与直梁桥在轴力、弯矩、剪力、扭矩等内力分布上的差别目前可供借鉴的设计、研究经验较少,但随着我国铁路事业的持续发展,连续弯梁使用的情况会越来越多,本文旨在通过对比某三线连续弯梁在直梁与弯梁两种模型下的受力情况,简化该弯梁桥的设计计算方法。
2 工程概况
新建北京动车段工程跨越南三环和京开高速公路处为五线并行铁路,京沪左线平面位于R=800 m曲线上,五线线间距5~5.02 m。每处各采用一联三线铁路大跨度预应力混凝土连续弯梁和一联双线铁路大跨度预应力混凝土连续弯梁。
三线铁路弯梁跨度为(71.94+122.29+72.17)m,采用单箱双室直腹板截面,箱梁各控制截面的梁高分别为:端支座处及边跨直线段和跨中处为5.0 m,墩顶处梁高9.0 m,墩底平段长4.8 m,梁高按二次抛物线变化。中跨跨中直线段长4.29 m,边跨直线段长分别为13.84 m和14.07 m,桥型布置如图1所示。
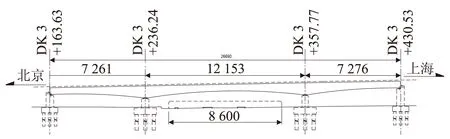
图1 连续弯梁立面布置图(京沪左线)(cm)
3 直梁模型与弯梁模型的对比分析
为考察连续箱梁在曲线与直线布置形式下受力特性的差别,采用有限元法对两种布置形式下结构的受力特性进行了详细计算。本次计算采用空间有限元程序MIDAS/Civil,为准确模拟连续弯梁桥的受力特点,在模型中支点、边支点支座对应的位置,共进行了8处一般约束进行等代模拟,分别模拟固定支座、纵向活动支座及横向活动支座。
3.1 有限元模型的建立
分别建立直梁、弯梁模型,着重分析二者受力差别。为便于分析比较,两种模型均采用梁单元,分别在主力和主力+附加力工况下进行分析比较,计算模型如图2、图3所示。

图2 弯梁有限元模型

图3 直梁有限元模型
3.2 内力分析对照
通过程序计算,两种模型的所有内力均为主力+附加力荷载工况控制。
3.2.1 轴力对照
主力+附加力荷载工况下,弯梁模型和直梁模型的轴力计算结果,如图4、图5所示。

图4 弯梁模型轴力图

图5 直梁模型轴力图
两种模型梁身各主要部位的轴力对照情况,如图6所示。

图6 两种模型轴力对照图
由轴力对比可以看出,弯梁模型和直梁模型计算结果规律基本一致,轴力相差较小,且弯梁模型轴力值除个别点外普遍比直梁模型小。
3.2.2 弯矩对照
主力+附加力荷载工况下,弯梁模型和直梁模型的弯矩计算结果,如图7、图8所示。

图7 弯梁模型弯矩图

图8 直梁模型弯矩图
两种模型梁身各主要部位的弯矩对照情况,如图9所示。

图9 两种模型弯矩对照图
由弯矩对比可以看出,弯梁模型和直梁模型计算结果规律基本一致,弯矩相差较小,且弯梁模型弯矩值普遍比直梁模型小。
3.2.3 剪力对照
主力+附加力工况下,弯梁模型和直梁模型的剪力计算结果,如图10、图11所示。

图10 弯梁模型剪力图

图11 直梁模型剪力图
两种模型梁身各主要部门的剪力对照情况,如图12所示。

图12 两种模型剪力对照图
由剪力对比可以看出,弯梁模型和直梁模型计算结果规律基本一致,剪力相差较小,且弯梁模型剪力值普遍比直梁模型小。
3.2.4 扭矩对照
主力+附加力工况下,弯梁模型和直梁模型的扭矩计算结果,如图13、图14所示。

图13 弯梁模型扭矩图

图14 直梁模型扭矩图
两种模型梁身主要部位的扭矩对照情况,如图15所示。

图15 两种模型扭矩对照图
由扭矩对比可以看出,弯梁模型与直梁模型扭矩的总体分布规律一致,但扭矩值相差较大,扭矩最大差值达64%。弯梁模型边跨最大扭矩发生在支点附近,中跨最大扭矩发生在中支点至1/4(3/4)中跨之间;边跨及中跨最小扭矩均发生在跨中附近。直梁模型边跨及中跨最大扭矩均发生在支点位置,最小扭矩均发生在跨中附近。
综上各对比结果,弯梁模型与直梁模型内力的差别主要体现在扭矩上。
3.3 应力分析对照
通过有限元模型计算分析,对截面四个控制点(如图16所示)的剪应力进行了计算统计,各个控制截面由扭转产生的剪应力和由荷载组合产生的组合应力的对照情况,如表1所示。

图16 箱梁截面应力主要控制点示意图

荷载分类截面应力点中支点截面中跨跨中截面中跨1/4截面边支点截面扭转应力组合应力百分比/%扭转应力剪应力百分比/%扭转应力剪应力百分比/%扭转应力剪应力百分比/%主力组合10.1411.381.240.22-13.71-1.610.652.3627.61-0.24-0.4454.592-0.1412.53-1.13-0.22-15.041.47-0.652.28-28.550.24-0.45-52.433-0.14-11.241.25-0.2216.65-1.33-0.65-2.6724.440.240.5146.6240.14-12.07-1.170.2217.601.260.65-2.61-24.96-0.240.52-45.47主+附组合10.1512.411.230.22-13.98-1.600.723.0723.59-0.25-2.2611.282-0.1513.83-1.11-0.22-15.571.43-0.722.86-25.300.25-2.24-11.363-0.15-11.291.36-0.2217.73-1.26-0.72-3.4321.110.251.2121.0640.15-12.28-1.250.2219.031.170.72-3.34-21.64-0.250.95-26.78
注:“百分比”指扭转应力占组合应力值的百分比。
由表1可知,中支点与中跨跨中截面由扭转产生的剪应力与组合应力值的比值非常小,均不超过1.7%。但中跨1/4截面与边支点截面由扭转产生的应力与组合应力值的比值较大,最大达到54.59%,说明连续弯梁桥中跨1/4截面与边支点截面的扭矩较大,这也与扭矩图显示的结果一致。
4 结论
4.1 参考同类公路桥梁设计成果
人民交通出版社2005年出版的《桥梁设计常用数据手册》中有以下结论:当曲线梁桥采用具有相当抗扭刚度的闭口截面时,对于曲线梁段的扭转跨径所对应的中心角小于12°时,曲线梁桥可以采用以曲线长为跨径的直线桥进行结构分析。
本文的研究对象三线连续弯梁中跨所对应的中心角8.7°小于12°,按照上述规定,可以采用等跨径的直梁模型进行结构分析。
4.2 根据有限元计算结果对比分析
从有限元计算结果比较来看,弯梁模型和直梁模型总体计算结果规律基本一致,轴力、弯矩、剪力值相差均较小,且弯梁模型计算值普遍比直梁小。弯梁模型与直梁模型内力的差别主要体现在扭矩上,支点附近扭矩较大。由于箱梁截面抗扭刚度较大,通过适当配置抗扭钢筋可以解决箱梁抗扭问题。
4.3 最终研究结论
根据人民交通出版社2005年出版的《桥梁设计常用数据手册》的规定,以及经过有限元程序的验证,得出北京动车段工程跨京开高速公路特大桥三线铁路预应力混凝土连续弯梁采用直梁模型进行结构分析,并加强抗扭配筋验算的计算方式,进而简化了三线连续弯梁的结构计算,可为同类铁路桥梁的设计与研究提供借鉴。
[1] 郑建.中国高速铁路桥梁[M].北京:高等教育出版社,2008. ZHENG Jian.Chinese high-speed railway bridges [M].Beijing: Higher Education Press, 2008.
[2] 王召祜.客运专线桥梁设计研究[J].铁道标准设计,2005,21(4):26-31. WANG Zhaohu.Research on Design of Passenger Dedicated Line Bridge [J].Railway Standard Design,2005,21(4):26-31.
[3] 朱伯芳.有限单元法原理与应用(第二版)[M].北京:水利水电出版社,1998. ZHU Bofang.Principle and Application of Finite Element Method (Second Edition) [M].Beijing: China Water & Power Press,1998.
[4] 过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003. GUO Zhenhai,SHI Xudong. Principle and Analysis of Reinforced Concrete [M].Beijing:Tsinghua University press,2003.
[5] GB 50010-2002 混凝土结构设计规范[S]. GB 50010-2002 Code for Design of Concrete Structures[S].
[6] 范立础.预应力混凝土连续梁桥[M].北京:人民交通出版社,2001. FAN Lichu.The Prestressed Concrete Continuous Girder Bridge [M].Beijing: China Communications Press, 2001.
[7] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2003. LI Guohao. Stability and Vibration of Bridge Structure[M]. Beijing: China Railway Publishing House, 2003.
[8] 王勖成.有限单元法[M].北京:清华大学出版社,2003. WANG Xucheng. Finite Element Method[M].Beijing: Tsinghua University press, 2003.
[9] 孙广华.曲线桥梁计算[M].北京:人民交通出版社,1997. SUN Guanghua. Curved Bridge Calculation [M].Beijing: China Communications Press, 1997.
[10]《桥梁设计常用数据手册》编委会.桥梁设计常用数据手册[M].北京:人民交通出版社,2005. Editorial board of Bridge Design Data Manual. Bridge Design Data Handbook,[M]. Beijing: China Communications Press, 2005.
[11]黄剑源.薄壁结构的扭转分析-曲线梁与斜支箱形梁[M].北京:中国铁道出版社,1981. HUANG Jianyuan. Torsional Analysis of Thin-walled Structures-Curved Girder and Skew Box Girder [M]. Beijing: China Railway Publishing House, 1981.
Study on Simplified Calculation of Three-line Railway Long Span Continuous Curved Beam
SONG Shufeng
(Third Railway Survey and Design Institute Group Corporation, Tianjin 300142, China)
Three-line railway curved beam bridge is featured by wide deck, big ratio of structural width and span, large torques of some cross sections and complex stress, and currently there are few designs and research experience of railway bridges in China for reference. Taken the three-line railway prestressed concrete continuous curved beam of super major bridge across the Jing-Kai high-speed railway in Beijing EMU Depot as the research object, through the finite element program, element models of straight beam and curved beam are established separately. On the basis of the comparision and analysis of the internal forces for the two models and the highway bridge design achievements for reference, it is concluded that the straight beam model can be adopted for the overall structural stress analysis, and then, the structure calculation way of the three-line continuous curved beam bridge is simplified, the difficulty of the design is reduced, the design efficiency is improved, and also references for similar bridge design and calculation are provided.
three-line railway; curved beam; straight beam; simplified calculation; finite element
2016-02-26
宋树峰(1982-),男,工程师。
1674—8247(2016)03—0019—04
U442
A
