立体几何中的显隐问题

房 亮

(贵州省赛文高级中学，贵州 兴义 562400)

立体几何中的显隐问题

房 亮

(贵州省赛文高级中学，贵州 兴义 562400)

本文从立体几何图形中基本的平面概念出发，来分析高考文科数学立体几何题型中因为一些隐藏的线、面给题目带来的视觉影响和解题限制，从而寻求一种关于立体几何中的显隐问题的解题策略。

高考；立体几何；显隐问题

立体几何在高考中占据重要的地位。通过近几年的高考情况分析，考察的重点及难点稳定。高考始终把直线与直线、直线与平面、平面与平面平行或垂直的性质和判定作为考察重点。在难度上也始终以中等偏难为主。在高考考目题中，从2015高考新课标全国卷2题目中要求在立体几何图形中做出满足要求的辅助线，不用说明理由。当时此题的社会反响很大，其中大部分的反应是：立体几何题目不是应该出平行垂直的证明么？怎么画起正方形来了，是不是舍本逐末。这恰恰是立体几何运用的关键所在，在教学中很多学生将立体几何中的所有的线全部都画成了实线，显然学生缺乏空间想象能力，做题目时无法建立空间模型，对于异面直线位置关系不能很好的建立空间想象，所以会证明一些题目并不意味着具备空间想象能力，恰恰是这道高考题才能说明什么是应试、什么是能力，才能进行有效选拔。

例1：正方体ABCD-A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：

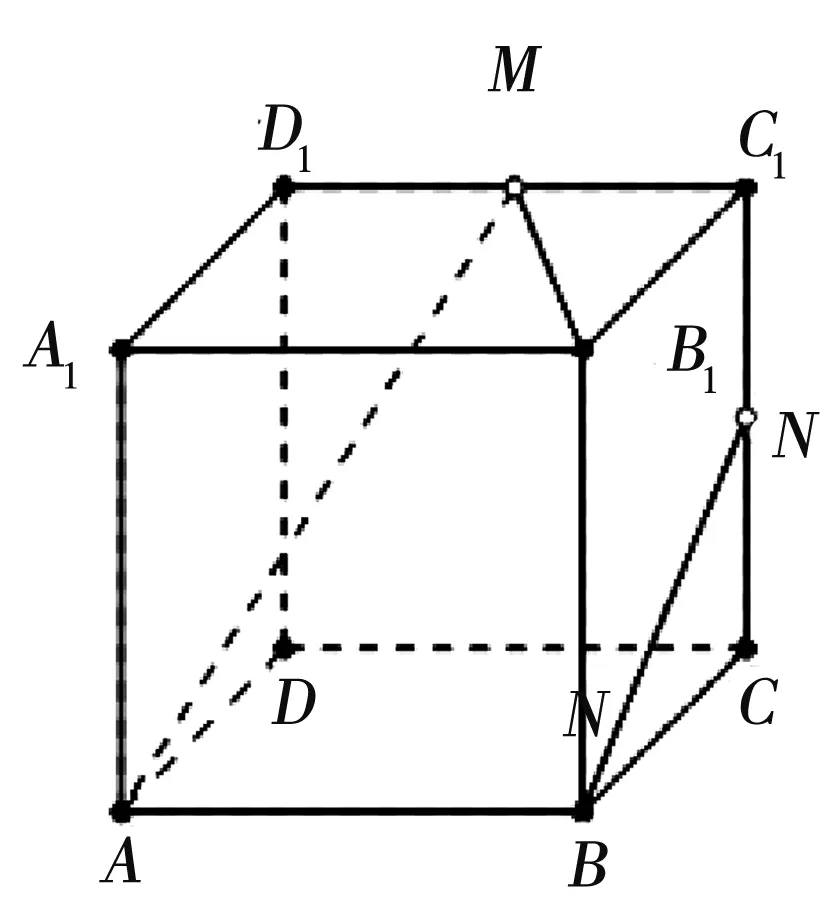
(1)直线AM与CC1是相交直线；

(2)直线AM与BN是平行直线；

(3)直线BN与MB1是异面直线；

(4)直线AM与DD1是异面直线。

其中正确的结论为________.

(注：把你认为正确的结论的序号都填上)

分析：此题(1)(2)可能会被误选，所以要将直线AM、BN继续延展显现出来。

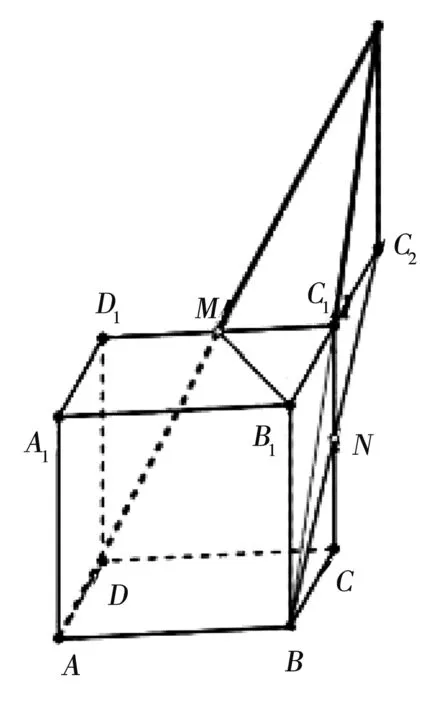
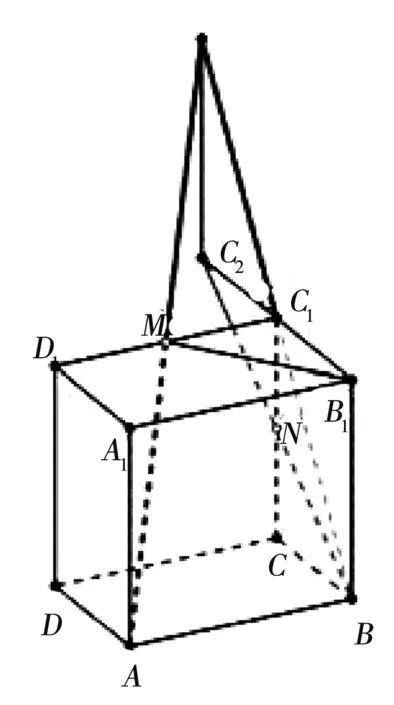
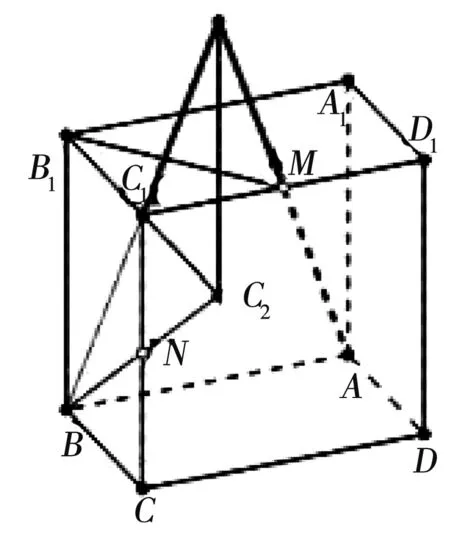
根据公理2的推论“两条平行直线确定一个平面”，由AB//MC1得ABMC1确定一个平面，所以将BC1与AM这两条不平行的直线延长一定会交于一点。如下图，所以(1)是错的。

将BN延长至点C2，所以(2)也是错的。正确答案为(3)(4)。

例2：如图，在正四棱柱A′C中，E、F、G、H分别是棱CC1、C1D1、D′D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M只需满足条件________时，就有MN//平面B′BDD′。

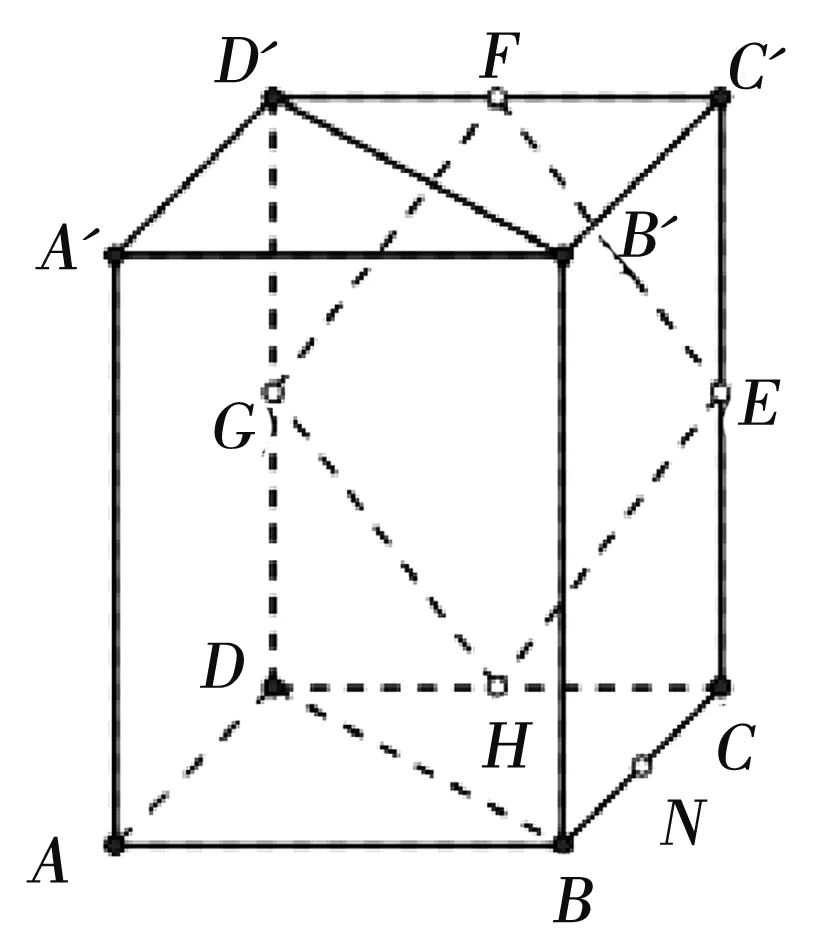
分析：此题过点N应有一个平面α与平面B′BDD′平行，则M在α内，又因点M在四边形EFGH内，所以M在两个平面的交线上，所以需要将α显现出来。

解答：因NH//BD，HF//BB′，所以平面NHF//平面B′BDD′ ，根据公理3，FHN确定一个平面NHF，而平面NHF∩四边形EFGH=FH，所以M在线段FH上。

例3：如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，AB=2，AF=1，M是线段EF的中点。

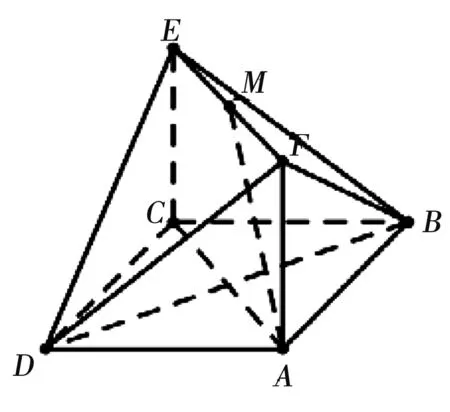
(1)求证：AM//平面BDE。

(2)若平面ADM∩平面BDE=n，平面ABM//平面BDE=m，试分析直线n与m的位置关系，并证明你的结论。

分析：第2问若想将直线m、n显现出来，有一定的难度，不好操作。但看到两问的联系AM不难找到突破口。

简答：AM//平面BDE，AM在平面ADM内，平面ADM∩平面BDE=n，所以AM//n；同理AM//m，根据公理4，m//n。

例4：如图，已知三棱柱ABC-A′B′C′，侧棱垂直于底面，AB=AC，∠BAC=90°，点M，N分别为A′B和B′C′的中点。

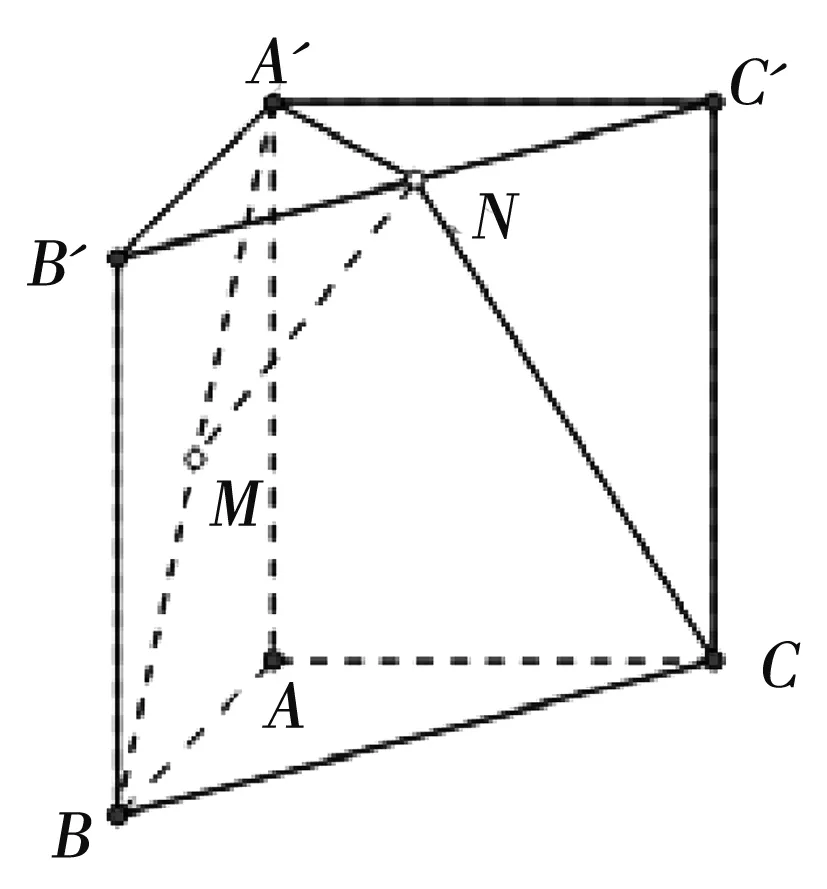
(1)证明：MN//平面AA′C′C；

(2)设AB=λAA′，当λ为何值时，CN⊥平面A′MN，

试证明你的结论。

分析：除A′N⊥CN外，平面A′MN在三棱柱中的截面没有完全显示，导致由CN⊥MN或CN⊥A′B无法解答或无法快速解答此题。

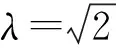
结论：在需要解答的题目中，要充分利用平面的延展性和显隐策略解题，即利用四个公理进行解题，适当的进行平面的延展，才能很直观的看到或找到解决问题的途径，这样才能够很好地体现学生空间想象能力的考察和空间几何问题的分析能力体现。

Explicit and implicit problem in stereo eometry

FANG Liang

(Saiwen Senior High School of Guizhou Province, Xingyi 562400, China)

Based on the basic plane concept in stereo geometric figure, this paper analyzes the visual influence and problem-solving limitation caused by some hidden lines and faces in stereo geometry of liberal arts mathematics in college entrance examination, so as to find problem-solving strategy of explicit and implicit problem.

College entrance examination; Stereo geometry; Explicit and implicit problem

2016-09-26

房亮(1980-)，男，学士，中学一级教师。

G634

B

1674-8646(2016)23-0031-02