基于bootstrap方法序约束下正态总体均值、方差的区间估计
2016-03-08国冰
国 冰
(吉林农业科技学院 文理学院,吉林 吉林 132101)
基于bootstrap方法序约束下正态总体均值、方差的区间估计
国 冰
(吉林农业科技学院 文理学院,吉林 吉林 132101)
讨论了在半序约束下正态总体均值和方差的区间估计问题,给出了基于bootstrap方法的迭代算法,通过模拟与传统交错迭代算法的结果进行了比较。
bootstrap方法;序约束;正态总体均值;区间估计;交错迭代算法
现阶段约束条件下的统计推断已成为统计分析中的一个重要领域。在我国,对约束条件下的统计推断和保序回归的研究也是刚刚起步。史宁中教授在1994年给出相对应的交错迭代算法[1],1998年又给出求在总体均值未知和方差已知的情况下,序约束下的正态总体均值和方差极大似然估计的算法[2]。但现阶段遇到的现实问题有两个,一是如何在半序条件下研究正态总体的均值和方差的估计。二是现实研究中的样本量都非常小,那么小样本试验中如何更好地利用样本中的信息量,这两个问题成为现阶段约束条件下统计推断的主要研究内容和主要发展趋势。本文希望借助bootstrap方法的抽样思想来加大信息量,从而更好地给出序约束下正态总体的均值和方差区间估计。
1 保序回归
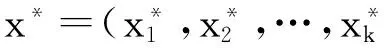
下面给出求保序回归的PAVA算法[3]:
步骤1:若x∈G,则x*=x,
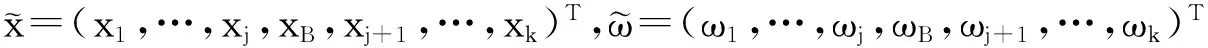
步骤3:重复步骤2,直到把下标集B分解成l个块B1,…,Bl,满足AV(B1)<… 我们可以证明x*确实是x的保序回归。 令xij,j=1,2,…,ni,表示来自第i个正态总体的观测值,i=1,2,…k,则对数似然函数为: 对于大样本的数据,我们可以应用交错迭代算法[1]来求解(μ,σ2)的极大似然估计,但样本量较小的时候,样本所提供的信息较少,现有的交错迭代算法效果就会不好。这时我们利用抽样的bootstrap方法来增大样本的信息量,再利用交错迭代算法求解参数的保序回归,并利用样本百分数来得到(μ,σ2)的区间估计,以上就是基于bootstrap的迭代算法的基本思想。 下面给出基于bootstrap方法的迭代算法: [1]ShiN-Z.MaximumLikelihoodEstimationofmeansandvariancefromnormalpopulationsundersimultaneousorderrestrictions[J].MultivariateAnal,1994,(49):282-294. [2]ShiN-Z.,JiangH.MaximumLikelihoodEstimationofisotonicnormalmeanswithunknownvariance[J].MultivariateAnal,1998,(64):183-195. [3] 史宁中.保序回归与最大似然估计[J].应用概率统计,1993,(02):203-215. Intervalestimation of mean and variance of normal population based onbootstrap algorithm GUO Bing (School of Arts and Science, Jilin Agricultural Science and Technology College, Jilin 132101, China) This article discusses the problem of normal populations with unknown means and variance under simultaneous order restrictions, gives the iterative method based on the bootstrap, and compares the results of the simulative and traditional alternating iterative methods. Bootstrap algorithm; Order constraint; Normal population mean; Interval estimation; Interleaving iterative algorithm 2016-09-03 吉林农业科技学院青年基金项目(2014210) 国冰(1979-),男,讲师,理学硕士。 O211 A 1674-8646(2016)23-0023-022 算法

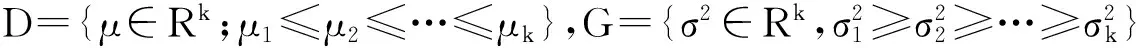



3 模拟与结果

