基于图像边缘位移的有监督的稀疏表示分类方法

廖 亮， 杨程凯

(中原工学院 电子信息学院， 河南 郑州 451191)

基于图像边缘位移的有监督的稀疏表示分类方法

廖 亮， 杨程凯

(中原工学院 电子信息学院， 河南 郑州 451191)

稀疏表示分类算法在有监督的图像识别上有广泛的应用.该分类算法的准确度与训练样本个数有很大的关联.通常训练样本越充分，则该算法分类准确率越高，然而遇到小样本问题时，该算法分类准确率会明显降低.针对小样本问题，提出使用基于图像边缘位移的方法，得到和原始训练图像样本高度相关的新样本，达到扩充训练样本容量的目的，进而提高算法的分类准确率.同时，对于带仿射约束的稀疏表示分类算法，也可以经过图像边缘位移方法来提高分类准确率.实验结果证明，所用方法能够取得较好的图像识别效果.

图像分类；稀疏表示；训练样本；仿射约束

0 引 言

在近年来的机器视觉领域中，有监督的图像分类技术(SupervisedImageClassification，SIC)一直是该领域关注的热点[1].该技术针对目标图像，利用提取的有效图像特征，通过匹配已知训练集的图像信息，寻找出与测试图像最相近的训练图像所在的类，从而达到图像分类的目的[2].现有的多数有监督的图像分类算法的分类准确率和训练样本个数有非常密切的关系.一般情况下，只有足够多的样本才能够获得较好的分类准确率.目前，稀疏表示分类算法(SparseRepresentation-basedClassifier,SRC)[3]是比较有效的图像识别算法之一.它利用所有训练样本，对待测试样本进行线性表示.当训练样本足够多时，通过计算线性向量的最小1范数，将测试样本分类到距离最近的类中.与现有多数方法相比，SRC借助于1范数的最小化，在分类准确率和鲁棒性都有理论上的保证[4].然而在实际应用中常常会遇到小样本问题，这将影响SRC算法的分类精度.解决小样本问题，是SRC方法所不得不面对的现实问题[5].

1 SRC算法基本理论

原始训练图像有N类，可以表示成矩阵A=[A1,A2，…，AN].每类含有M个训练样本，其中第i类训练样本可以表示成矩阵，Ai=[vi,1,vi,2，…，vi,M]，vi,j表示第i类中第j个图像样本，是大小为m×n的灰度图像，在矩阵Ai中的每个样本将展成列向量，即vi,j∈MN.根据线性子空间原理[6]，若给出属于第i类的测试样本y，则y可表示成有足够多的第i类训练样本的线性叠加，

y=αi,1vi,1+αi,2vi,2+…+αi,Mvi,M

(1)

式中，αi,j∈，j=1,2,…，M

由于A表示N类目标的所有训练样本所组成的矩阵，所以可以用所有训练样本对测试样本y进行线性表示，其矩阵形式的表达式如下，

y=Ax

(2)

x*=argminx‖x‖0s.t. y=Ax

(3)

x*=argminx‖x‖1s.t. y=Ax

(4)

式中，‖·‖0表示0范数，‖·‖表示1范数.

2 基于图像边缘位移的训练样本及扩充

若SRC的训练样本数越多，所获得的x就越稀疏，即训练集样本数越多，SRC的分类准确率就越好.对于现实中小样本的情况，可以通过位移矩阵和傅里叶变换实现图像的最外层像素的循环位移，得到与原始图像特征极为近似的扩充图像，从而达到扩充原始训练集的目的，同时可以得到扩充图像的类别.

1)定义位移矩阵.

定义1 位移矩阵：对尺寸为m×n的图像要求行位移数为r，列位移数为c，给定尺寸为m×n的位移矩阵S，满足下面条件，

(5)

式中，0≤r≤m-1,0≤c≤n-1且r,c均为整数.

为了使图像尽可能保持原本的特征信息，对于r,c将选取4种情况，

(6)

这4种情况下得到的位移矩阵分别对应于S1，S2，S3，S4.

2)对原始训练集进行二维快速傅里叶变换，变换后的各个图像矩阵点乘二维傅里叶变换后的位移矩阵，进行二维傅里叶反变换得到基于图像边缘位移的图像，并以此来扩充原始训练集，从而达到增加分类准确率的目的.

3 实验与结果

在实验中，选择目前常用的ORL人脸数据库作为实验数据集[8]，以满足训练样本较少而图像尺寸较大的情况.其中ORL人脸数据库共有40个类，每个类仅含10幅112×92像素图像，每幅图像拥有不同的细节和角度[8].该数据集的一个样本示例如图1所示.

图1ORL数据库示例

本研究模拟小样本问题，将对样本的各个类别进行3次随机抽样，依次抽取1、2及3个样本，从而从多方面来验证所提方法的性能.对抽样过后的训练集进行基于图像边缘位移的训练样本集扩充方法，选取上述提出的4种位移矩阵，同时对比未扩充SRC和扩充未受仿射约束SRC，以及扩充并受仿射约束SRC.在不同的较低维数和不同的每类原始训练样本个数的环境下，对各个分类器的分类精度进行比较，这样可以看出显著差异.在实验中，特征将选取10到40维的不同维数，并观察每类训练样本个数分别为1、2及3时各个分类器的分类结果，统计结果数据如表1、2和3所示.

表1 每类训练样本为1时的分类精度

表2 每类训练样本为2时的分类精度

表3 每类训练样本为3时的分类精度

同时，相对应的MATLAB仿真结果图如图2、图3和图4所示.

图2 每类样本为1时的分类精度

图3 每类样本为2时的分类精度

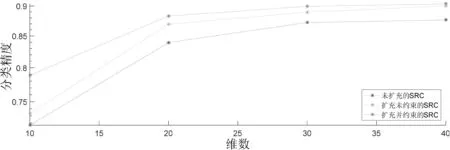
图4 每类样本为3时的分类精度

图2～4中，从上至下的折线依次代表的是样本未扩充SRC、样本自扩充的未受仿射约束SRC、样本自扩充的受仿射约束SRC.

实验数据表明，经过扩充样本并受仿射约束SRC的分类准确率最高.

4 结 语

通过实验数据可以看出，虽然随着原始样本个数的增多，各个分类精度的差距会随之缩小，但基于样本自扩充的受仿射约束SRC的分类精度始终保持最高，而且当处于小样本问题时，本研究提出的基于图像边缘位移的有监督的稀疏表示分类方法要比其他情况下SRC分类结果高得多.对于小样本问题，实验结果显示，无论是否受仿射约束，基于图像边缘位移的有监督的稀疏表示分类方法都能有效提高分类准确率.因此，本研究所提出的基于样本自扩充的受仿射约束SRC，利用样本自扩充，将训练样本包含信息量最少的最外层像素经过循环移位来扩充训练集样本个数，同时通过受仿射约束SRC对扩充样本的系数进行受限，从而在原始样本较少的情况下，能够稳定提高分类准确率.

[1]WrightJ,YangAY,GaneshA,etal.Robust face recognition via sparse representation[J].IEEETransPatternAnalMachIntell,2008，31(2):210-227.

[2]YangJ,ZhangL,XuY,etal.Beyond sparsity:The role of L1-optimizer in pattern classification[J].PatternRecogn,2012，45(3)：1104-1118.

[3]雷明军,彭进业.改进SRC算法在人脸识别中的应用[J].电子设计工程,2013，21(4)：137-139.

[4]MichaelElad.Sparse and redundant representations：from theory to applications in signal and image processing[M].NewYork，USA:Springer,2010.

[5]DonohoDL.For most large underdetermined systems of linear equations the minimal[J].CommPureApplMath，2006，59(6):797-829.

[6]XuY，LiXL，LaiZH，etal．Integrating conventional and inverse representation for face recognition[J].IEEETransCybern，2014，44(10):1738-1746．

[7]AT&T.The ORL Database of Faces[EB/OL].[2002-01-01].http://www.cl.cam.ac.uk/Research/DTG/attarhive/pub/data/att-faces.tar.Z.

[8]WoldS,EsbensenK,GeladiP.Principal component analysis[J].ChemometrIntellLabSys,1987,2(13):37-52．

Classification Method of Supervised Sparse Representation Based on Image Edge Displacement

LIAOLiang,YANGChengkai

(School of Electric and Information Engineering, Zhongyuan University of Technology, Zhengzhou 451191, China)

Sparse Representation-based Classifier(SRC) is widely used in supervised image recognition.However,the accuracy of SRC is tightly associated with the number of training samples.The more the training samples are,the more accurate the SRC is.However,when small sample problems occur,the accuracy of SRC decreases.As for the small sample problems,the paper puts forward a method based on image edge displacement to obtain new samples which are highly associated with the original training samples in order to expand the training sample capacity and therefore to increase the classification accuracy of SRC.Meanwhile,as for the SRC with affine constraints,the classification accuracy of SRC can be further improved by image edge displacement.The experiments show that the above-mentioned method can help achieve much more accurate image recognition.

image classification;sparse representation;training samples;affine constraints

1004-5422(2016)04-0355-03

2016-09-01.

廖 亮(1975 — )， 男， 博士， 副教授， 从事复杂图像识别与分类研究.

TP391.41

A