基于积分方程等效电路和BLT方程的传导耦合效应仿真分析
2016-03-07李福林韩继红张畅
李福林 韩继红 张畅
(1. 解放军信息工程大学,郑州 450001;2. 军队信息安全重点实验室,郑州 450001)
基于积分方程等效电路和BLT方程的传导耦合效应仿真分析
李福林1,2韩继红1,2张畅1
(1. 解放军信息工程大学,郑州 450001;2. 军队信息安全重点实验室,郑州 450001)
提出了基于积分方程等效电路和Baum-Liu-Tesche(BLT)方程的电磁脉冲传导耦合效应分析方法,建立外部电磁干扰等效源模型,提取等效电流和阻抗参数. 对内部含复杂传输线网络和集成电路插件的电子设备建立了电磁拓扑模型,采用BLT方程分析电磁脉冲响应. 仿真分析了内部传输线连接关系、外部信号线长度和半径大小、节点负载等因素对传导耦合效应的影响. 将计算结果和商用电磁仿真软件CST的结果进行了对比,分析了所提方法的有效性, 可为电子设备电磁脉冲防护设计提供参考.
传导耦合;积分方程等效电路;矩量法;电磁拓扑;BLT方程
引 言
为满足通信和动力需要,现代电子设备箱体上通常都连接有必不可少的信号线、电源线等线缆.在外部电磁脉冲辐照下,这些线缆成为感应电流通过传导耦合方式进入设备内部的重要途径,可能造成电子元器件性能下降、状态反转、结点击穿,甚至是烧毁整个电子元器件,妨碍电子设备的正常运行和作用发挥.开展电磁脉冲传导耦合效应机理研究,对于探索相应的防护措施、增强电子设备的生存能力具有重要意义.
线缆的电磁脉冲效应研究通常通过数学建模和仿真的方法来进行,如电路分析方法、电磁场全波分析方法等[1-4]. 电路分析方法将电磁脉冲传播过程以集总参数的电路元件进行描述,分析电压和电流的传输特性. 全波分析方法从麦克斯韦方程组出发,解特定边界条件下的电磁场波动方程,求得场量随时间和空间的变化规律,分析传输线上电磁波的传输特性. 电路分析方法简单高效,但随着外部干扰信号频率的上升,电磁场的传播很难用集总参数进行有效的描述. 电磁场全波分析方法能全面反映问题的物理机制,但在复杂结构建模和数值计算时比较困难,限制了其实际工程应用. 近年来,许多学者利用场路协同仿真的方法来研究场线耦合问题,兼具电路分析方法的高效性和全波分析方法的准确性,成为相关领域的一个研究热点[4-17].
文献[8]使用有限元法、文献[9-14]使用矩量法计算线缆与屏蔽箱体结合点处的感应电流, 建立由等效电阻和短路电流组成的外部电磁干扰等效源模型, 分析了多层印制电路板(Printed Circuit Board,PCB)连接线的传导耦合效应,但所使用的方法存在高频信号时域积分方程求解的后时稳定性不佳、适用频段较低等局限性. 文献[15-16]将时域干扰信号变换到频域,并结合矩量法和频域电磁场混合势积分方程求解干扰信号的等效电流源参数,扩展了干扰源等效建模方法的适用范围,但在对内部电路进行分析时,仅使用电路仿真软件对单传输线连接PCB板铜质印刷线的情形进行了仿真分析,未对内部存在复杂传输线网络的情形做理论分析. 实际的电子设备内部大都存在复杂的传输线网络和集成电路(Integrated Circuit, IC)插件,文章使用积分方程等效电路法建立外部电磁干扰源的等效模型,基于BLT方程[18-19]分析内部存在复杂传输线网络和集成电路插件的电子设备传导耦合效应,更加接近电子设备的实际,可进一步促进场路协同仿真方法的实际工程应用,为加强电子设备电磁安全防护提供参考.
1 理论分析
文章在对电子设备进行电磁脉冲传导耦合效应分析时将其分为内外两个区域,外部区域由连接线缆和屏蔽机壳组成,内部区域由传输线网络连接的高速集成电路组成. 具体分析流程为:1)采用积分方程等效电路法建立外部电磁干扰的等效源模型,使用矩量法计算电磁场混合势积分方程,获取等效源模型的参数;2)利用电磁拓扑理论中管道和节点的概念[20-23],对传输线网络和集成电路插件进行电磁拓扑分析,建立内部电路的电磁拓扑模型;3)将外部等效源模型的输出作为内部电路的输入,基于BLT方程计算各个节点的干扰电压响应.
1.1 积分方程等效电路法建立干扰等效源模型
假设电子设备的连接线缆和屏蔽机壳均为理想导体,外部电磁波入射到连接线缆和屏蔽机壳在其表面产生感应电流,其电流密度为J(r),Es(J(r))是J(r)产生的散射电场,Ei(r)为入射场,由边界条件,在导体表面S处,总切向电场等于零,即:
[Ei(r)+Es(J(r))]tan=0,r∈S.
(1)
Es(J(r))可由矢势A和电势φ表示:
Es(J(r))=-jωA(r)-φ(r).
(2)
式(2)中的矢势A和电势φ可分别由式(3)和式(4)表示:
(3)

(4)
式中:ε表示自由空间的电导率;μ为磁导率; j表示虚数符号;ω为辐射电磁场的角频率;k为波数;r为场点(x,y,z)的位置矢量;r′为源点的(x′,y′,z′)的位置矢量;R=|r-r′|表示源点到场点的距离.
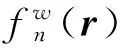
(5)

(6)
式(6)可以写成如式(7)所示的线性矩阵方程:
(7)
式中:Vp、Ip均为长度为Np的列向量,分别表示广义电压和广义电流;Zpq是一个Np×Nq的矩阵,表示广义阻抗,p,q=w,s,d.
通过LU分解,求解式(7),可以得到电流展开系数和整个箱体的表面感应电流分布. 通过已得到的感应电流参数,也可以获得阻抗矩阵等其他等效参数,建立外部电磁干扰的等效源模型.
1.2 基于电磁拓扑理论建立内部电路模型
电磁拓扑理论主要解决两类问题,一是外部电磁场通过电子设备外部的电源线、信号线或其他外露的导线进入系统内部形成的干扰,二是由于电子设备的不良屏蔽引入的干扰.
运用电磁拓扑理论分析具有复杂传输线网络的电子设备电磁脉冲响应时,先利用拓扑学的概念对系统进行分解,将设备内的集成电路插件抽象为 “节点”,将传输线抽象为“管道”,形成系统电磁拓扑图,用以描述电磁系统各个部分之间的耦合关系.

图1 电子设备内部结构示意图

图2 传输线网络模型图
对图1所示的电子设备内部结构,用变量N表示节点,用变量P表示管道,其电磁拓扑模型如图2所示.
1.3 基于BLT方程计算节点干扰电压
在运用电磁拓扑理论建立的内部电路电磁拓扑模型的基础上,基于集总源激励的多导体传输线网络模型,依据传输线理论并结合节点处入射电压和反射电压的叠加原理[24-29],得到入射电压、反射电压方程组,将各节点电压方程整理成矩阵方程的形式,建立多导体传输线网络BLT方程. 将外部电磁干扰等效源模型的输出作为内部电路电磁拓扑模型的输入,通过求解耦合关系所对应的BLT方程,得到系统各个节点的电磁响应.
首先建立双导体传输线的BLT方程,然后将其扩展至传输线网络的情形.
1.3.1 双导体传输线BLT方程
图3给出了一个均匀双导体传输线,其特征阻抗、导纳、传播常数和长度分别为Zc、Yc、γ、L,终端负载的阻抗为ZL1和ZL2,由位于x=xs处的集总电压源Vs或电流源Is激励.
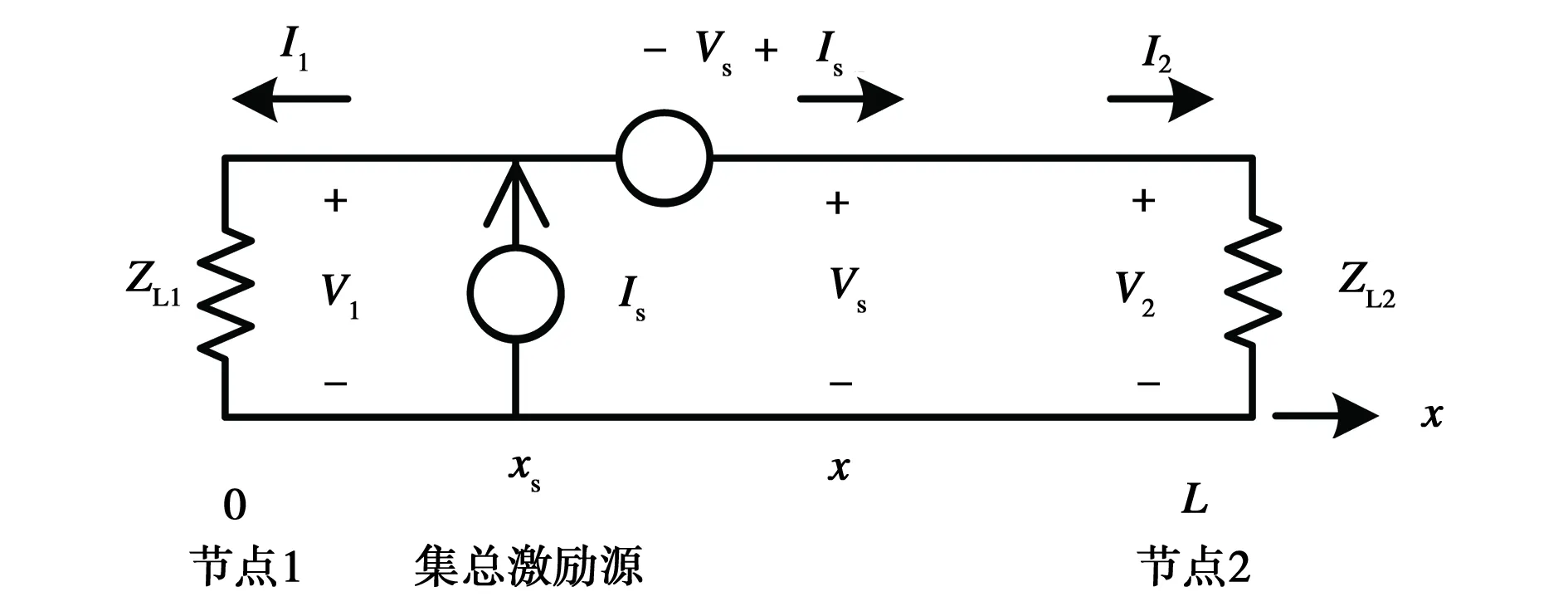
图3 双导体传输线模型
由传输线基本理论,传输线沿线存在正向行波V+(x)和逆向行波V-(x),如图4所示.

图4 双导体传输线信号流图
传输线上任一点x处的电压V(x)可表示为V+(x)和V-(x)之和,即:
V(x)=V+(x)+V-(x).
(8)
对电流Is有:
I(x)=I+(x)+I-(x).
(9)
方程(8)、(9)的通解为:
(10)
由x=xs处的边界条件可得:
(11)
由式(8)~(11)可得:
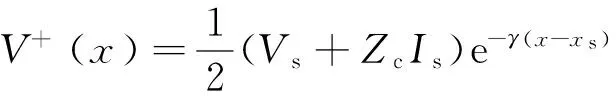
V-(x)=0(x>xs);
(12)

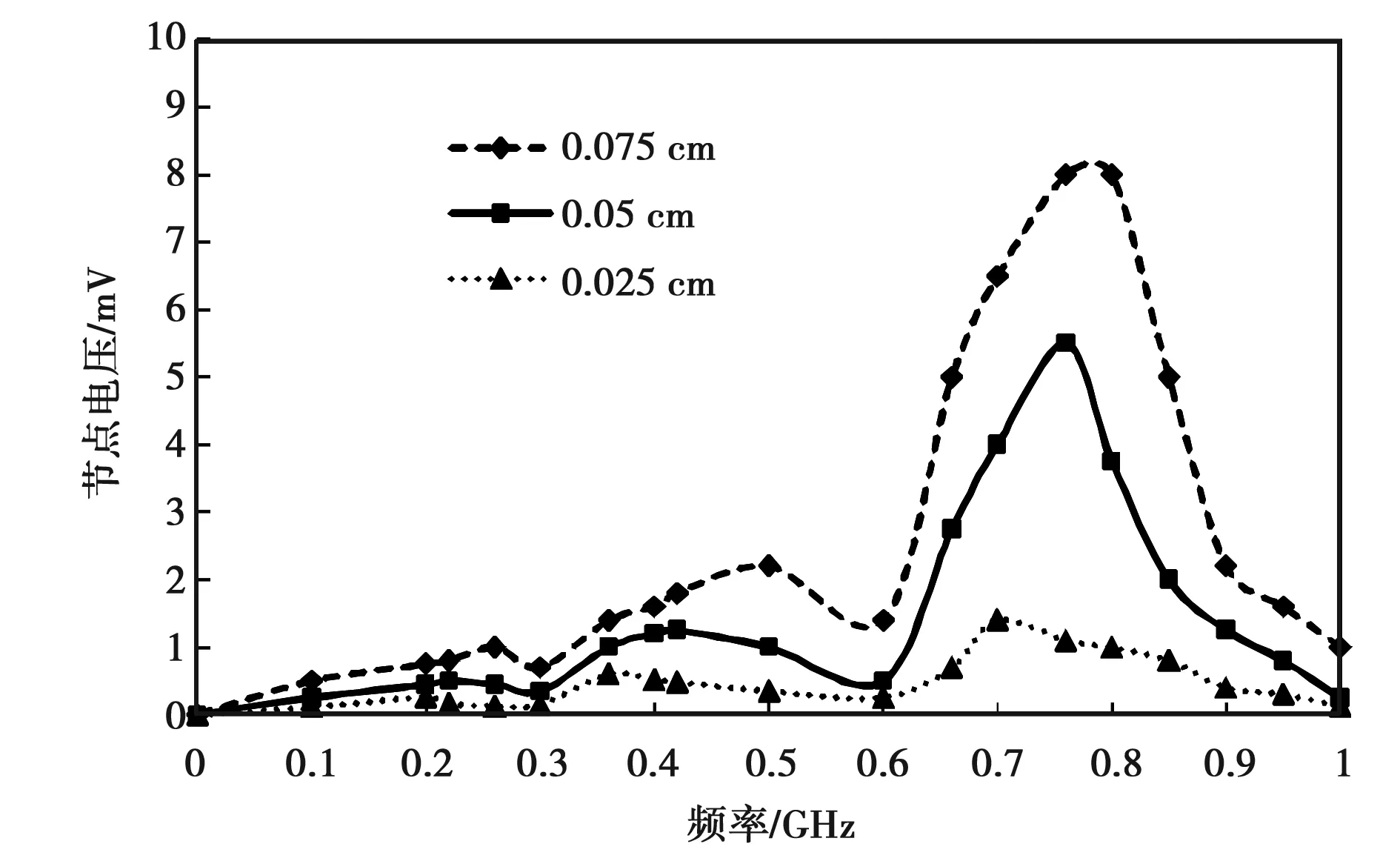
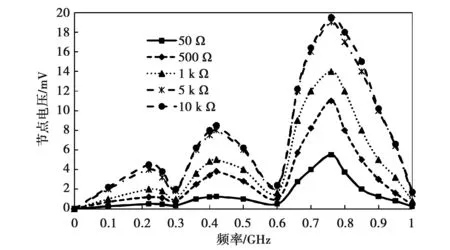
V+(x)=0(x (13) (14) 对节点2,有: (15) 在存在激励源的情况下,节点2的入射电压波等于节点1的入射电压波和激励源产生正向电压波之和,即: (16) 同理,节点1的反射电压波等于节点2的反射电压波和激励源产生的反向电压波之和: (17) 将式(16)和(17)写成矩阵方程的形式: (18) 设ρ为电压反射系数,则对任一节点m,有: (19) 对节点1和节点2,有: (20) (21) 将式(21)代入式(18)并整理: (22) 节点处的总电压为: (23) 将式(22)代入式(23),得到双导体传输线的BLT方程: (24) 1.3.2 传输线网络BLT方程 对传输线网络,BLT方程的一般形式为: V=[I+S]·[Γ-S]-1·VS (25) 式中:V表示节点的总电压超向量;I表示单位超矩阵;S表示散射超矩阵,包含网络中所有节点的散射参数;Γ表示传输超矩阵,包含网络中所有管道的传输参数;VS表示激励源超向量.下面给出式(25)中S、Γ和VS的表达式. 1)散射超矩阵S 假设网络中的节点均为非理想节点,ZL为节点的阻抗矩阵,Zc为节点所连管道的特性阻抗矩阵. 则散射超矩阵S的元素为: (26) 2)传输超矩阵Γ 将每个节点的传输矩阵按管道升序排列到一个矩阵的对角线上,其它元素为0,可以得到整个网络的传输超矩阵,具体形式如下: (27) 3)激励源超向量VS 将每个管道的激励向量按管道排列得到传输线网络的激励源超向量: (28) 2.1 外部电磁干扰等效源模型计算结果 对图1所示的电子设备,假设其屏蔽外壳和信号传输线均为理想导体,屏蔽外壳尺寸为12.5 cm×7.5 cm ×1.9 cm,信号线长度50 cm、半径0.05 cm,PCB为双层板,下层为铜质接地层,上层为IC插件和铜质带状连接线,中间是介电常数为2.1的绝缘介质. 采用幅值为1 V/m的平面波照射,传播方向与信号线垂直、电场极化方向与信号线平行,基于积分方程等效电路法求得外部电磁干扰等效源模型的感应电流,其幅值和相位随频率变化的曲线如图5和图6所示. 图5 等效源感应电流幅值随频率变化曲线 图6 等效源感应电流相位随频率变化曲线 2.2 内部电路电磁耦合效应仿真结果 假设设备内部各管道对应的传输线长度均为4 cm,各节点端接负载均为50 Ω,节点Ni对应的散射系数为Si,则 (29) (30) (31) 由系统结构的对称性,选择节点1、2、3、5和6作为观察点,各节点输出电压计算结果如图7所示. 图7 各节点输出电压随频率变化曲线 从图7中可以看出,各节点输出电压的最大值都出现在0.76 GHz,按输出电压值从大到小排序,与外部信号线直接相连的节点1最大,然后依次是节点2、节点5、节点3、节点6. 选择节点1和节点3,将本文方法的计算结果与电磁仿真软件CST的仿真结果进行对比,结果如图8所示. 图8 计算结果与CST仿真结果对比图 从图8中可以看出,本文方法的计算结果和CST软件的仿真结果吻合较好. 为考查外部信号线长度对节点输出电压的影响,保持信号线半径大小为0.05 cm不变,分别设置信号线长度为25 cm、50 cm、100 cm,考查节点2的输出电压随频率的变化情况,结果如图9所示. 图9 信号线长度不同时节点2的输出电压 从图9中可以看出,随着信号线长度的增加,节点2输出电压的最大值不断增大,且最大值所对应的频率值逐渐降低. 为考查外部信号线半径大小对节点输出电压的影响,保持信号线长度为50 cm不变,分别设置信号线半径为0.025 cm、0.05 cm、0.075 cm,考查节点2的输出电压随频率的变化情况,结果如图10所示. 图10 信号线半径不同时节点2的输出电压 从图10中可以看出,随着信号线半径的增加,节点2输出电压的最大值不断增大,最大值所对应的频率值逐渐升高. 为考查负载大小对节点输出电压的影响,保持信号线半径大小为0.05 cm,长度为50 cm,节点2对地的负载分别取50 Ω,500 Ω,1 kΩ,5 kΩ,10 kΩ,考查节点2的输出电压随频率的变化情况,结果如图11所示. 图11 节点2负载大小不同时的输出电压 从图11中可以看出,随着节点负载的增大,节点的输出电压逐渐增大,但负载增大到一定值后相当于开路,此时再增大负载,节点输出电压的峰值几乎不变.在保持箱体形状尺寸、信号线长度和半径不变的情况下,节点出现峰值的频率与负载的大小无关. 场路协同仿真方法既具有全波分析方法的准确性,又具有电路分析方法的高效性,成为电磁脉冲效应分析相关领域的一个研究热点. 论文使用积分方程等效电路法建立了外部电磁干扰的等效源模型,基于电磁拓扑理论和BLT方程分析了内部含复杂传输线网络和集成电路插件的电子设备传导耦合效应,仿真分析了内部传输线连接关系、外部信号线长度和半径大小、节点负载等因素对电磁脉冲效应的影响,结果与电磁仿真软件CST吻合较好. 论文的研究可进一步促进场路协同仿真方法的实际工程应用,为加强电子设备的电磁安全防护提供参考. [1] 王川川, 汪连栋, 曾勇虎, 等. 场线耦合问题研究现状及其发展综述[J].中国电子科学研究院学报, 2014, 9(4): 353-359. WANG C C, WANG L D ZENG Y H, et al. The present research and development trend of transmission line system’s coupling with electromagnetic fields[J]. Journal of CAEIT, 2014, 9(4): 353-359. (in Chinese) [2] 刘胜, 葛亚明, 李军. 平面波对传输线耦合响应的仿真研究[J]. 系统仿真学报, 2008, 20(6): 1619-1622. LIU S, GE Y M, LI J. Coupling response simulation of transmission lines excited by plane wave[J]. Journal of system simulation, 2008, 20(6): 1619-1622. (in Chinese) [3] 李贵兰, 李国新, 汪佩兰. 基于场线耦合理论的电爆装置射频感应电流仿真研究[J].系统仿真学报, 2011, 23(2): 265-269. LI G L, LI G X, WANG P L. RF induced current simulation of electro-explosive device based on field coupling to line theory[J]. Journal of system simulation, 2011, 23(2): 265-269. (in Chinese) [4] 刘尚合, 刘卫东. 电磁兼容与电磁防护相关研究进展[J]. 高电压技术, 2014, 40(6): 1605-1613. LIU S H, LIU W D. Progress of relevant research on electromagnetic compatibility and electromagnetic protection[J]. High voltage engineering, 2014, 40(6): 1605-1613.(in Chinese) [5] ANTONINI G. A spectral formulation for the transient analysis of plane-wave coupling to multiconductor transmission lines[J]. IEEE transactions on electromagnetic compatibility, 2009, 51(3): 792-804. [6] YANG Q X, ZHANG X, CHEN H Y, et al. Direct field-circuit coupled analysis and corresponding experiments of electromagnetic resonant coupling system[J]. IEEE transactions on magnetics, 2012, 48(11): 3961-3964. [7] TANG M, LU J, MAO J, et al. A systematic electromagnetic-circuit method for EMI analysis of coupled interconnects on dispersive dielectrics[J]. IEEE transactions on microwave theory and techniques, 2013,61(1):1-13. [8] 张爱民, 张杭, 陈德桂, 等. 具有屏蔽机壳的电子设备系统级电磁敏感性分析方法[J]. 西安交通大学学报, 2007, 41(2): 190-194. ZHANG A M, ZHANG H, CHEN D G, et al. Analysis method of electromagnetic susceptibility for electronic devices with shielded enclosure at system level[J]. Journal of Xi’an Jiaotong University, 2007, 41(2): 190-194. (in Chinese) [9] YUAN W L, LI E P. Electromagnetic susceptibility analysis in device level with numerical technique based on electric field integral equation[C]//International Symposium on Electromagnetic Compatibility. IEEE, 2004, 1:102-106. [10]YUAN W L, LI E P. A systematic coupled approach for electromagnetic susceptibility analysis of a shielded device with multilayer circuitry [J]. IEEE transactions on electromagnetic compatibility, 2005, 47(4): 692-700. [11]PHYU H N, LI E P, YUAN W L. Analysis of electromagnetic susceptibility on high speed circuits located in a shielded enclosure[C]//Proceeding of 17th International Zurich Symposium on Electromagnetic Compatibility. IEEE, Piscataway, USA, 2006: 312-315. [12]郝建红, 孙娜燕, 高璞, 等. 场路结合法分析设备电磁辐照效应[J]. 电波科学学报, 2012, 27(2): 359-364. HAO J H, SUN N Y, GAO P, et al. Analysis of the electromagnetic radiation effect of the equipment by field-circuit method[J]. Chinese journal of radio science, 2012, 27(2): 359-364. (in Chinese) [13]高璞. 电子设备屏蔽壳的电磁感应模型及电磁敏感性研究[D]. 北京: 华北电力大学, 2011. GAO P. Study on electromagnetic induction model and electromagnetic susceptibility of electronic equipment shielded enclosure [D]. Beijing: North China Electric Power University, 2011. (in Chinese) [14]高璞, 王飞, 郝建红, 等. 基于场积分方程的机箱耦合电流特性的数值分析[J]. 电子质量, 2010(5): 77-80. GAO P, WANG F, HAO J H, et al. Numerical simulation on enclosure joint-point current coupling characteristics base on electric field integral equation [J]. Electronics quality, 2010(5): 77-80. (in Chinese) [15]郝建红, 范杰清. 电磁脉冲耦合效应的等效源建模及应用[J]. 强激光与粒子束, 2014, 26(6): 063024. HAO J H, FAN J Q. Modeling and application of equivalent source of electromagnetic pulse coupling effects [J]. High power laser and particle beams, 2014, 26(6): 063024. (in Chinese) [16]范杰清. 复杂金属腔体高功率微波耦合效应研究[D]. 北京: 华北电力大学, 2015. FAN J Q. Study on effect of HPM coupling on complex metal cavity[D]. Beijing: North China Electric Power University, 2015. (in Chinese) [17]孙凤杰, 邓建红. 电子学系统强电磁脉冲干扰场路结合仿真[J]. 强激光与粒子束, 2015, 27(12): 178-182. SUN F J, DENG J H. Field-circuit co-simulation of electromagnetic pulse interference to electronics[J]. High power paser and particle beams, 2015, 27(12): 178-182. (in Chinese) [18]BAUM C E, LIU T K, TESCHE F M. On the analysis of general multi-conductor transmission line networks[J]. Interaction note, 1978, 350:1-26. [19]BAUM C E. Including apertures and cavities in the BLT formalism [J]. Electromagnetics, 2005, 25(7/8): 623-635. [20]林竞羽,周东方,毛天鹏,等.电磁拓扑分析中的BLT 方程及其应用[J].信息工程大学学报, 2004, 5(2): 118-121. LIN J Y, ZHOU D F, MAO T P, et al. BLT equation in electromagnetic topology analysis and its application[J]. Journal of Information Engineering University, 2004, 5(2): 118-121.(in Chinese) [21]蒋义勇. 系统高功率微波效应仿真方法研究[D]. 合肥: 安徽大学, 2007. JIANG Y Y. Research on simulation method of high power microwave effects [D]. Hefei: Anhui University, 2007. (in Chinese) [22]王利萍, 周东方, 彭强, 等. 基于拓扑网络的屏蔽腔体内置微带线响应分析[J]. 电波科学学报, 2014, 29(1): 321-327. WANG L P, ZHOU D F, PENG Q, et al. Response analysis of microstrip lines in the shielding cavity based on topological network[J]. Chinese journal of radio science, 2014, 29(1): 321-327. (in Chinese) [23]阚勇, 闫丽萍, 赵翔, 等. 基于电磁拓扑的多腔体屏蔽效能快速算法[J]. 物理学报, 2016, 65(1): 030702. KAN Y, YAN L P, ZHAO X, et al. Electromagnetic topology based fast algorithm for shielding effectiveness estimation of multiple enclosures with apertures [J]. Acta physica sinica, 2016, 65(1): 030702.(in Chinese) [24]安霆, 刘尚合. 基于BLT方程的电磁干扰建模[J].高电压技术, 2007, 33(12): 55-58. AN T, LIU S H. Modeling for electromagnetic interaction by the BLT equation[J]. High voltage engineering, 2007, 33(12):55-58.(in Chinese) [25]高雪莲, 张晓宇, 赵磊, 等. 基于BLT方程的复杂线缆网络电磁干扰响应求解[J].科学技术与工程,2015,15(5):248-252.(in Chinese) GAO X L, ZHANG X Y, ZHAO L, et al. Analysis of electromagnetic interference by using the BLT equation on the complex cable network[J]. Science technology and engineering, 2015,15(5):248-252.(in Chinese) [26]王宝和. 电磁拓扑中BLT方程的建立及应用研究[D]. 长沙: 国防科学技术大学, 2006. WANG B H. The deductions and applications of BLT equation in electromagnetic topology[D]. Changsha: National University of Defense Technology, 2006. (in Chinese) [27]王为, 刘培国, 覃宇建. BLT-FDTD时频结合分析传输线瞬态响应[J]. 微波学报, 2010(S2):25-28. WANG W, LIU P G, QIN Y J. Hybrid BLT-FDTD approach for the transient response of transmission lines[J]. Journal of microwaves, 2010(S2):25-28. (in Chinese) [28]张祥, 石立华, 周颖慧, 等.复杂传输线网络电磁脉冲响应的拓扑分析研究[J]. 电波科学学报, 2013, 28(2): 341-347. ZHANG X, SHI L H, ZHOU Y H, et al. Terminal voltage analysis of complex transmission line network based on electromagnetic topology theory[J]. Chinese journal of radio science, 2013, 28(2): 341-347. (in Chinese) [29]鱼群, 王亚弟, 韩继红, 等. BLT 方程的时域扩展及其在微带线中的应用[J].系统工程与电子技术, 2011, 33(11): 2372-2376. YU Q, WANG Y D, HAN J H, et al. Development of the BLT equation in the time domain and its application in line[J]. Systems engineering and electronics, 2011, 33(11): 2372-2376.(in Chinese) Simulation of conducted coupling effects based on IEEC and BLT equation LI Fulin1,2HAN Jihong1,2ZHANG Chang1 (1.PLAInformationEngineeringUniversity,Zhengzhou450001,China;2.PLAKeyLaboratoryofInformationSecurity,Zhengzhou450001,China) A method based on integral equation equivalent circuit(IEEC) and Baum-Liu-Tesche(BLT) equation is proposed to analyze conducted coupling effects of the electromagnetic pulse. The method is adopted to get the equivalent source model, corresponding current and resistance parameters of external electromagnetic interference. Furthermore, electromagnetic pulse effects of the electronic equipment with complex transmission line network and integrated circuit are computed by the electromagnetic topology theory and BLT equation. Finally, the influence of transmission line topology, the signal line length, radius and the node load resistance on conducted coupling effects is analyzed. Experimental results are consistent with simulation results of CST software, which proves the validity of the presented method. The research and simulation results can provide reference to the electromagnetic protection design of the electronic equipment. conducted coupling;integral equation equivalent circuit;method of moments;electromagnetic topology;Baum-Liu-Tesche equation 10.13443/j.cjors.2016102501 2016-10-25 国防科研项目 TM15 A 1005-0388(2016)06-1180-08 李福林 (1979-),男,河北人,解放军信息工程大学博士研究生,副教授,主要研究方向为电子设备电磁脉冲效应分析. 韩继红 (1966-),女,山西人,解放军信息工程大学教授,博士生导师,博士,主要研究方向为电子设备电磁脉冲效应分析及安全防护、安全协议分析与验证. 张畅 (1981-),男,湖北人,解放军信息工程大学博士研究生,讲师,主要研究方向为电子设备电磁安全防护. 李福林, 韩继红, 张畅. 基于积分方程等效电路和BLT方程的传导耦合效应仿真分析[J]. 电波科学学报,2016,31(6):1180-1187. LI F L, HAN J H, ZHANG C. Simulation of conducted coupling effects based on IEEC and BLT equation[J]. Chinese journal of radio science,2016,31(6):1180-1187. (in Chinese). DOI: 10.13443/j.cjors.2016102501 联系人: 李福林 E-mail: leefulin@163.com DOI 10.13443/j.cjors.2016102501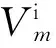
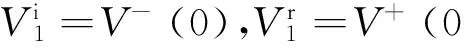

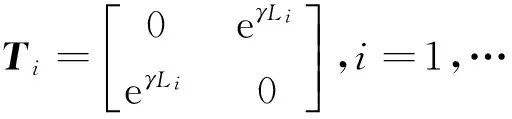
2 仿真结果分析





3 结 论



